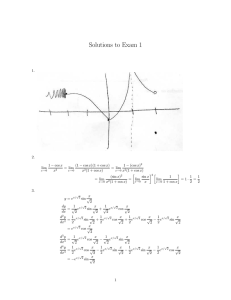
PHYSICS 505: CLASSICAL ELECTRODYNAMICS HOMEWORK 7 3 Problem 5.3 Let us consider a right-circular solenoid of finite length L and radius a with N turns per unit length, each carrying current I. In the continuum limit of the current densities on the surface of the solenoid, we are to show that the magnetic induction on the cylindrical axis is µ0 N I (cos θ1 + cos θ2 ) , 2 where the angles are given in a clear diagram not included here. Bz = We can solve this problem rather directly by using our result from problem (5.1) above. There, we showed that the magnetic induction from a closed current is given in terms of the gradient of the solid angle subtended by the circular current (with appropriate conventions for signs). Because of the cylindrical symmetry in the problem at hand, we see that at a particular z, Z 1 Ω = 2π d cos θ = 2π(1 − cos θ). cos θ Notice that z = a cos θ and so Ω is only a function of z. Hence without loss of generality, ∂Ω . ∂z Because of the linearity in the induction, the total field Bz will be given in terms of an integral over the individual currents over z. Therefore, Z L µ0 N I ∂Ω ˆ0 z, Bz (z) = dz 0 4π ∂z 0 0 µ0 N I = (Ω(L) − Ω(0)) , 4π µ0 N I (1 − cos(π − θ2 ) − 1 + cos θ1 ) , = 2 ∇Ω = ẑ ∴ Bz = µ0 N I (cos θ1 + cos θ2 ) . 2 Problem 5.5 (c) We are to derive approximations for the z- and ρ-components of the magnetic induction near ρ = 0 and cosθ2 → 0. Being at one of the ends of the solenoid is equivalent to having cos θ vanish for one of the two angles defined for problem (5.3). This reduces the induction to Bz = µ0 N I cos θ1 , 2 where cos θ2 = 0. If the solenoid were long, then cos θ1 can be well-approximated by its Taylor expansion. ∴ Bz = ¢ µ0 N I µ0 N I ¡ . 1 − O(θ2 ) ' 2 2 We will have a similar expression estimating the ρ-component. To obtain this expression, we recall that Bz = µ02N I cos θ1 . Because z = a cos θ1 in our coordinates, this implies that Bz = µ02N I az . Therefore, ∂Bz µ0 N I = . ∂z 2a Now, by the vanishing divergence of the magnetic induction and the independence of B on φ, we see that ∂Bz 1 ∂ (ρBρ ) + = 0. ∇·B= ρ ∂ρ ∂z Using our work above, this implies that ∂ µ0 N I (ρBρ ) = ± ρ. ∂ρ 2a 4 JACOB LEWIS BOURJAILY Notice that the ambiguity of sign represents which end of the solenoid we are interested in. This differential equation has the trivial solutions ρBρ = ± which implies directly that Bρ ' ± µ0 N I ρ2 , 4 a µ0 N I ³ ρ ´ . 4 a Problem 5.6 Let us consider a cylindrical conductor of radius a with a hole of radius b bored parallel to, and displaced a distance d from, the cylindrical axis (with b + d < a). The current density is uniform throughout the remaining metal and is parallel to the axis. We are to use Ampère’s law and principle of linear superposition to find the magnitude and direction of the magnetic flux-density in the hole. By the linear superposition principle, this problem is identical to one in which we consider the combination of two cylindrical conductors, one of radius a with a uniform current density and no hole and another with opposite current located at the whole. By Ampère’s law in integral form, we know the magnetic induction for a uniform cylindrical conductor. Only the component normal to the line integral is important, and so only Bφ will be non-vanishing. In particular, we have that µ0 I µ0 πρ2 J 1 Bφ = φ̂ = φ̂ = µ0 ρJ φ̂. 2πρ 2πρ 2 Now, the expression above did not require us to specify which wire we were discussing and so equally applies to both. Specifically, if ρ is the radial coordinate in the system of the larger main cylinder and ρ0 is radial coordinate of the system displaced by distance d, then we see that ³ ´ 1 B = µ0 J ρφ̂ − ρ0 φ̂0 . 2 Notice that we have implicitly included the fact that we want the currents to cancel each other in the region of the smaller cylinder. We notice, however, that if we write d~ ≡ ρ−ρ0 , then ẑ × d~ = ẑ ×ρ− ẑ ×ρ0 = ρφ̂ − ρ0 φ̂0 . Hance, we see that 1 ~ ∴ Btotal = µ0 J ẑ × d. 2