ATIESADORES

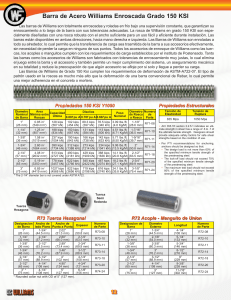
Capitulo IV
CAPITULO IV
4. METODOLOGÍA
4.1.
EJEMPLOS RESUELTOS NUMÉRICAMENTE
Las trabes armadas diseñadas para estos ejercicios no son necesariamente
las más económicas. Otras posibilidades incluyen una trabe con un alma más
delgada y con más atiesadores intermedios, o bien, una trabe con un alma más
gruesa y sin atiesadores intermedios. Dos variables que afectan el costo son el
peso (volumen requerido) y los costos de fabricación.
Aunque las trabes con los atiesadores intermedios requerirán usualmente
menos acero, los ahorros pueden ser cancelados por el costo adicional de
fabricación. También pueden considerarse los espesores variables para los
patines. Esta alternativa ahorrará peso, pero aquí también deben considerarse los
costos adicionales de la fabricación. Un enfoque práctico para lograr un diseño
económico consiste en preparar varias alternativas y comparar sus costos al usar
las estimaciones del material y los costos de fabricación.
Los ejercicios 4.1.1 y 4.2.2 fueron tomados del libro: Diseño de estructuras
de acero con LRFD del autor William T. Segui.
4.1.1. EJEMPLO 1
La trabe que se muestra en la Figura 4.1 debe ser revisada para ver si
cumple con las Especificaciones AISC. Las cargas son de servicio con una razón
de carga viva a carga muerta de 3.0 y el acero es A36. La carga uniforme de
34
Capitulo IV
4 kips ft incluye el peso de la trabe. El patín de compresión tiene un soporte lateral
en los apoyos y en los puntos de aplicación de las cargas concentradas.
El patín de compresión está restringido contra la rotación en esos mismos
puntos. Se tienen atiesadores de apoyo, como se muestra, en los extremos y bajo
las cargas concentradas. Los atiesadores están recortados una pulgada en el
borde interior, arriba y abajo, para librar las soldaduras entre los patines y el alma.
No se tienen atiesadores intermedios. Suponga que todas las soldaduras son
adecuadas y revise lo siguiente:
Figura 4.1 Trabe I sometida a peso propio y cargas puntuales.
a. Resistencia por flexión
b. Resistencia por cortante
c. Interacción flexión-cortante
35
Capitulo IV
d. Atiesadores de apoyo
Figura 4.2 Diagrama de Fuerzas Cortantes y Momentos Flectores.
•
Solución
El primer paso en el análisis consiste en determinar si este miembro
satisface la definición del AISC de trabe armada (ecuación 4.1 y 4.2):
63
h
=
= 168
3
tw
8
4.1
970
4.2
( )
Fy
=
970
36
= 161.7
36
Capitulo IV
Como
h 970
>
, este miembro en flexión es una trabe armada, por lo tanto,
tw
Fyf
se sigue con el análisis.
El alma debe satisfacer la limitación de la esbeltez del AISC. El valor limite
de
h
tw
dependerá de la razón del aspecto
a
. Para esta trabe armada, los
h
atiesadores de apoyo servirán como atiesadotes intermedios.
4.3
a 12(12)
≈
= 2.286
h
63
Esta razón es aproximada, porque a ≈ 12 ft . En los tableros interiores, 12
pies es la separación centro a centro entre los atiesadores y no la separación libre.
En los tableros extremos, a < 12 ft debido a los atiesadores dobles en los soportes.
Como
a
> 1.5 , se utiliza la ecuación 2.21:
h
14,000
Fyf (Fyf + 16.5)
= 322 >
h
= 168
tw
2.21
El alma cumple satisfactoriamente la limitación de esbeltez.
a. Resistencia por flexión.
La resistencia por flexión estará limitada por la resistencia del patín en
tensión o del patín en compresión. En cualquier caso, será necesario el modulo de
sección elástico de la sección, el cual por simetría; se calcula con la ecuación.4.4.
S xt = S xc = S x
4.4
37
Capitulo IV
En la Tabla 4.1 se muestra el cálculo del momento de inercia Ix con
respecto al eje fuerte.
COMPONENTE
A
I
D
I+Ad2
Alma
-
7814
-
7814
Patín
16
-
32
16380
Patín
16
-
32
16380
40574 in4
Tabla 4.1 Momento de Inercia, Ix.
El modulo de sección elástico se calcula con la ecuación 4.5:
Sx =
4.5
Ix 40,570
=
= 1248 in 3
c
32.5
El factor de trabe híbrida R e será necesario para la resistencia del patín en
tensión y para la resistencia del patín en compresión. Esta trabe es no híbrida, por
lo que: R e = 1
La resistencia del patín en tensión, con base en la fluencia, está dada por la
ecuación 2.5.
Mn = Sxt Re Fy = 1248(1.0)(36 ) = 44,930 kips - in
2.5
= 3744 kips - ft
La resistencia por pandeo del patín de compresión está dada por la
ecuación 2.6.
Mn = SxcRpg Re Fcr
2.6
38
Capitulo IV
donde el esfuerzo critico, Fcr , esta basado en el pandeo lateral torsional o en el
pandeo local del patín. Para revisar el pandeo lateral torsional, se necesita el radio
de giro rT . De la Figura 4.3.
Figura 4.3 Patín.
( )
h t w3
t f bf3
Iy =
+ 6
12
12
3
1
(1)(16 )3 + 1 (10.5) 3 8 = 341.4 in 4
Iy =
12
12
4.6
A = 16(1.0) + 10.5( 3 8 ) = 19.94 in 2
4.7
( )
rT =
4.8
341.4
Iy
=
= 4.138 in
19.94
A
Para hallar el valor de Fcr basado en el pandeo lateral torsional, se tiene
que:
Si λ ≤ λp , la falla será por fluencia.
Fcr = Fy
2.10
39
Capitulo IV
Si λ p ≤ λ < λr , la falla será por PLT inelástico.
Si λ > λr , la falla será por PLT elástico.
⎡ 1 ⎛ λ − λp
Fcr =C b Fy ⎢1 − ⎜
⎜
⎢⎣ 2 ⎝ λr − λ p
Fcr =
⎞⎤
⎟⎥
⎟
⎠⎥⎦
2.12
286,000C b
λ
2.11
2
La longitud no arriostrada del patín es de 12 ft y los parámetros de esbeltez
para el pandeo lateral torsional están dados por las ecuaciones 2.7 y 2.8.
λ=
2.7
Lb 12(12)
=
= 34.80
4.138
rT
λp =
300
Fyf
=
300
36
2.8
= 50
Fcr = Fy = 36 ksi
Como λ < λ p
2.10
Para hallar el valor de Fcr basado en el pandeo local del patín, se tiene que:
Si λ ≤ λ p , la falla será por fluencia.
Fcr = Fy
Si λ p ≤ λ < λr , la falla será por PLP elástico.
⎡ 1 ⎛ λ − λp
Fcr = C b Fy ⎢1 − ⎜
⎜
⎢⎣ 2 ⎝ λr − λ p
Si λ > λ r , la falla será por PLP elástico.
Fcr =
2.17
26,200k c
⎞⎤
⎟⎥
⎟
⎠⎥⎦
2.18
2.19
λ2
El esfuerzo critico, Fcr , será ahora calculado para el pandeo local del patín,
donde los parámetros de esbeltez necesarios se muestran en las ecuaciones 2.13
y 2.14.
λ=
λp =
bf
16
=
=8
2tf 2(1.0)
65
Fyf
=
65
36
= 10.83
2.13
2.14
40
Capitulo IV
Como λ < λ p
Fcr = Fy = 36 ksi
2.17
Para calcular el factor de reducción de resistencia, R PG , de la trabe
armada, será necesario el valor de ar que se obtiene con la ecuación 4.9:
[ ]
4.9
1
23.62
Aw 63 8
ar =
=
=
= 1.477 < 10
16
Af 16(1.0)
RPG = 1 −
= 1−
4.10
⎛ h 970 ⎞
ar
⎜ −
⎟ ≤1.0
1200 + 300ar ⎜⎝ t w
Fcr ⎟⎠
⎡
1.477
970 ⎤
168 −
⎢
⎥ = 0.9943
1200 + 300(1.477 ) ⎣
36 ⎦
El valor de R PG es casi 1.0, debido a que este miembro en flexión
escasamente califica como trabe armada y esta muy cerca de ser clasificado como
una viga.
De la ecuación 2.6, la resistencia nominal por flexión del patín de
compresión es.
Mn = SxcRPG Re Fcr = 1248(0.9943 )(1.0 )(36 )
= 44,670 kips - in = 3723 kips - ft
El
resultado
es
ligeramente
menor
que
2.6
la
resistencia
nominal
correspondiente al patín en tensión y, por lo tanto, gobierna. La resistencia de
diseño se calcula como se muestra en la siguiente ecuación 2.2:
φbMn = 0.9( 3723 ) = 3350 kips - ft
2.2
De la Figura 4.2 se obtiene que el momento máximo por carga factorizada.
Mu = 3168 kips - ft < 3350 kips - ft (satisfactorio)
41
Capitulo IV
b. Resistencia por cortante.
La resistencia por cortante es una función de la razón de esbeltez del alma
h
a
y de la relación de aspecto . Primero, se determina si se puede usar la
tw
h
acción de campo de tensión en regiones que no sean las de los tableros extremos.
a
es menor que 3.0 y menor que
h
Ella se utiliza cuando
⎡ 260
⎢
⎢h
⎣ tw
⎤
⎥
⎥
⎦
2
(ecuación 4.11).
4.11
2
2
⎡ 260 ⎤
260 ⎤
⎡
⎥ =
⎢
⎢ 168 ⎥ = 2.395
⎢h ⎥
⎣
⎦
⎣ tw ⎦
El valor aproximado de
a
es de 2.286, por lo tanto, se emplea la acción de
h
campo de tensión. Determinemos Kv de la ecuación 4.12.
Kv = 5 +
5
()
a 2
h
=5+
5
(2.286 )
2
4.12
= 5.957
Se halla ahora el valor de C v con la ecuación 3.4 o 3.5.
Para 187
Para
kv
kv
h
≤
≤ 234
Fyw t w
Fyw
kv
h
> 234
tw
Fyw
En la ecuación 4.1 se calculó
187
Cv =
Cv =
kv
h
3.4
Fyw
tw
44,000kv
(h t ) F
3.5
2
w
yw
h
, con las ecuaciones 4.13 y 4.14 se
tw
establecen los límites.
42
Capitulo IV
kv
5.957
= 187
= 76.07
Fyw
36
4.13
k
5.957
234 v = 234
= 95.19
36
Fyw
4.14
187
Como
Kv
h
= 168 > 234
tw
Fyw
Cv =
44,000kv
(h t ) F
2
w
⎡
⎢
1 − Cv
Vn = 0.6 AwFyw ⎢Cv +
⎢
1.15 1 + a
h
⎣
( )
2
=
yw
44,000(5.957 )
= 0.2580
(168 ) 2 (36 )
3.3
⎤
⎥
⎥
⎥
⎦
⎡
1 − 0.2580
= 0.6(23.62)(36)⎢0.2580 +
1.15 1 + (2.286 ) 2
⎢⎣
3.5
⎤
⎥ = 263.6 kips
⎥⎦
φvVn = 0.90(263.6) = 237 kips
3.1
Del diagrama de cortante de la Figura 4.2, la fuerza cortante máxima
factorizada en la mitad de la trabe es Vu = 102 kips . Por lo que la resistencia por
cortante es adecuada donde se permite la acción de campo de tensión.
En los tableros extremos no se permite la acción de campo de tensión y la
resistencia por cortante se calcula con la ecuación 4.15.
Vn=0.6 AwFywCv=0.6(23.62 )(36 )(0.2580 )=131.6 kips
φvVn = 0.90(131.6) = 118 kips
4.15
3.1
De la Figura 4.2 obtenemos que la carga máxima factorizada en el tablero
extremo es:
Vu = 234 kips > 118 kips (no satisfactorio)
43
Capitulo IV
Se tienen dos opciones para incrementar la resistencia por cortante:
Incrementar el espesor del alma o disminuir la razón de aspecto de cada tablero
extremo al agregar un atiesador intermedio. En este caso, se opta por agregar
atiesadores.
Para la posición de los atiesadores intermedios tiene que calcularse “ a ”
usando el siguiente procedimiento:
Despejando el valor de Cv de la ecuación 4.15 y obtenemos la ecuación
4.16.
φvVn = φv (0.6 AwFywC v )
4.15
φvVn
4.16
Cv =
φv (0.6 AwFyw )
=
234
= 0.5096
0.90(0.6)(23.62)(36 )
Después, se despeja kv de la ecuación 3.5.
Cv =
44,000kv
⎛h
⎜⎜
⎝ tw
3.5
2
⎞
⎟⎟ Fyw
⎠
2
⎛h⎞
Cv ⎜⎜ ⎟⎟ Fyw
t
0.5096(168 ) 2 (36 )
=
= 11.77
kv = ⎝ w ⎠
44,000
44,000
4.17
Finalmente, se despeja “ a ” de la ecuación 4.12.
kv = 5 +
a
=
h
4.12
5
⎛a⎞
⎜ ⎟
⎝h⎠
2
5
5
=
= 0.8594
kv − 5
11.77 − 5
4.18
La separación requerida entre los atiesadores (ecuación 4.19) es de:
44
Capitulo IV
a = 0.8594h = 0.8594(63) = 54.1 in
4.19
Figura 4.4 Separación de atiesadores.
Aunque “ a ” se define como separación libre, se tratará aquí, de manera
conservadora, como una separación centro a centro y se colocará el primer
atiesador intermedio a 54 in, desde el extremo de la trabe. Esta posición dará una
resistencia de diseño aproximadamente igual a la fuerza cortante máxima
factorizada de 234 kips. Ningún atiesador adicional será necesario ya que la carga
cortante factorizada fuera de los tableros extremos es menor que la resistencia de
diseño de 237 kips, (ver Figura 4.4).
La resistencia por cortante no es adecuada. Agregar un atiesador intermedio a 54
pulgadas desde cada extremo de la trabe, ver Figura 4.2 (cargas factorizadas).
c. Interacción por flexión-cortante.
La interacción flexión-cortante debe ser revisada cuando se tiene un campo
de tensión (fuera de los tableros extremos) y cuando se cumplen las siguientes
condiciones:
1.- La carga cortante factorizada esta en el siguiente rango:
45
Capitulo IV
0.6φVn ≤ Vu ≤ φVn
Para esta trabe, este rango de cortante fuera de los tableros extremos seria:
0.6(237 ) ≤ Vu = 234 ≤ 237
142 klb ≤ Vu = 234 ≤ 237 klb
2.- El momento por carga factorizada esta en el siguiente rango:
0.75φMn ≤ M u ≤ φM n
Para esta trabe, el rango seria:
0.75(3350 ) ≤ M u = 3168 ≤ 3350
2510 klb - ft ≤ M u = 3168 ≤ 3350 klb - ft
La interacción de la flexión y cortante no tiene que ser revisada.
d. Atiesadores de apoyo.
Los atiesadores de apoyo se proporcionan en cada carga concentrada.
Para los atiesadores de apoyo interiores y en los soportes se tiene la ecuación
3.16.
95
Fy
=
95
b 7.5
= 10 (satisfactorio)
= 15.8 > =
6
t 0.75
3.16
Para los atiesadores de apoyo interiores, se calcula primero la resistencia
por aplastamiento. De la ecuación 4.22:
Apb = 2at = 2(7.5 − 1)(0.75 ) = 9.750 in 2
4.20
Rn = 1.8FyApb = 1.8(36)(9.750 ) = 631.8 kips
4.21
φRn = 0.75(631.8) = 474 kips > 60 kips (satisfactorio)
4.22
46
Capitulo IV
Figura 4.5 Atiesadores de apoyo.
Se revisa la resistencia del atiesador como miembro en compresión
(ecuación 4.29) (ver Figura 4.5.).
A = 2(0.75 )(7.5) + ( 3 8 )(9.375 ) = 14.77 in 2
(
I = ∑ I + Ad
2
)
2
3
⎡ 0.75(7.5)3
9.375(3 8 )
⎛ 7 .5 3 8 ⎞ ⎤
=
+ 2⎢
+ 7.5(0.75 )⎜
+ ⎟ ⎥ = 227.2 in 4
12
12
2 ⎠ ⎦⎥
⎝ 2
⎢⎣
4.23
4.24
I
227.2
=
= 3.922 in
A
14.77
4.25
KL Kh 0.75(63)
=
=
= 12.05
r
r
3.922
4.26
r =
λc =
Fcr =
0.75h
πr Fy 29000
> 1.5 entonces,
0.877
Fy = 35.72 ksi
λ2c
4.27
4.28
47
Capitulo IV
φcPn = φcFcrA = 0.85(35.72 )(14.77) = 449 kips > 60 kips
(satisfactorio)
4.29
Para los atiesadores de apoyo en los soportes, de la Figura 4.5 la
resistencia de diseño por aplastamiento se calcula con la ecuación 4.22:
φRn = φ (1.8FyApb )
= 0.75(1.8)(36)[4(6.5)(0.75)] = 948 kips > 234 kips
4.22
(satisfactoria)
Revisamos el conjunto atiesador-alma como un miembro en compresión,
con referencia a la Figura 4.6.
(
)
I = ∑ I + Ad 2 =
2
3
⎡ 0.75(7.5)3
4.5(3 8 )
⎛ 7 .5 3 8 ⎞ ⎤
+ 2⎢
+ 7.5(0.75 )⎜
+ ⎟ ⎥ = 454.3 in 4
12
12
2 ⎠ ⎦⎥
⎝ 2
⎣⎢
⎛3⎞
A = 4.5⎜ ⎟ + 4(0.75)(7.5) = 24.19 in 2
⎝8⎠
r=
4.24
4.23
4.25
454.3
I
= 4.334 in
=
24.19
A
La relación de esbeltez se calcula con la ecuación 4.26.
Kh 0.75(63)
=
= 10.90
r
4.334
4.26
0.75h
4.27
λc =
Fcr =
πr Fy 29000
0.877
λ
2
c
> 1.5 entonces,
4.28
Fy = 35.77 ksi
φcPn = φcFcrA = 0.85(35.77 )(24.19) = 736 kips > 234 kips
(satisfactorio)
4.29
Por lo tanto, los atiesadores de apoyo son adecuados.
48
Capitulo IV
Figura 4.6 Conjunto atiesador-alma.
4.1.2. EJEMPLO 2
Diseñe una trabe armada simplemente apoyada con un claro de 60 pies
que debe soportar las cargas de servicio que se muestran en la Figura 4.7.
Considere acero A36 y electrodos E60xx. Suponga que la trabe tiene un soporte
lateral continuo.
•
Solución
Las cargas factorizadas, excluido el peso de la trabe, se muestran en la
Figura 4.8
W = 1.2(WD ) + 1.6(WL )
4.30
W = 1.2 (1.7) + 1.6 (1.25) = 4.04 klb/ft
P1 = 1.2(PD1 ) + 1.6(PL1 )
4.31
P1 = 1.2 (78) + 1.6 (58) = 186.4 klb
49
Capitulo IV
Figura 4.7 Cargas de servicio.
Figura 4.8 Cargas factorizadas y diagramas de momento y cortante.
50
Capitulo IV
El peralte general se determina con la ecuación 4.32.
Longuitud del claro 60(12)
=
= 65.45 in
11
11
4.32
El espesor del patín debe ser estimado, las consecuencias de una
estimación pobre son menores, por lo tanto se usará un peralte de 65 in y un
espesor t f de patín de 1.5 in y una altura de alma dada por la ecuación 4.33.
h = 65 - 2(1.5) = 62 in
4.33
Para determinar el espesor del alma, se examinan primero los valores límite
de
h
. Para que este miembro a flexión califique como trabe armada debe cumplir
tw
con la ecuación 2.1.
2.1
h
970
970
≥
=
= 161.7
tw
Fyf
36
tw ≤
Para
tw ≥
Para
tw ≥
4.34
62
h
=
= 0.383 in
161.7 161.7
a
≤ 1 .5
h
h 2000 2000
≤
=
= 333.3
tw
Fyf
36
4.35
62
= 0.186 in
333.3
a
> 1 .5
h
2.20
h
14,000
14,000
≤
=
= 322.0
tw
Fyf (Fyf + 16.5)
36(36 + 16.5)
4.36
62
= 0.192 in.
322.0
Ensáyese una placa de alma de
2.21
1
in Χ 62 in .
4
51
Capitulo IV
Determínese el tamaño requerido de patín, ecuación 4.38.
A w = h(t w )
4.37
A w = 62 (1 4) = 15.5 in 2
Af =
Mu
A
4614(12)
62(1/ 4)
− w =
−
= 24.97 in 2 .
0.90hFy
6
0.90(62)(36 )
6
4.38
Con la ecuación 4.40 puede estimarse el peso de la trabe.
Total = A w + 2(Af )
4.39
Total = 62 ( 1 4) + 2 (24.97) = 65.45 in2
3.4(Total )
1000
3.4 ( 65.45)
= 0 .22
Peso =
1000
Peso =
4.40
Figura 4.9 Cargas y diagramas incluido el peso propio.
52
Capitulo IV
El
momento
flexionante
ajustado
se
muestra
en
la
Figura
4.9:
Mu = 4714 kips - ft
El área requerida para un patín se muestra en la ecuación 4.38:
Af =
Mu
A
4714(12)
62(1 / 4)
− w =
−
= 25.57 in 2
0.90hFy
6
0.90(62)(36)
6
4.38
bf =
Af 25.57
= 17.1 in
=
tf
1. 5
4.41
1
Ensáyese dos placas de patín de 1 in X 17 in
2
1
Ensáyese con una placa de patín de 1 in x 17 in y con una placa de alma de
2
1
in x 62 in , como se muestra en la Figura 4.10.
4
Figura 4.10 Seccion transversal propuesta.
Se revisa la resistencia a la flexión de la trabe armada:
53
Capitulo IV
a) Fluencia del patín en tensión.
tw h 3
2
+ 2t f bf (Cgf )
12
(1 / 4 )( 62 )3
Ix =
+ 2(1.5 )(17 )(31.75 )2 = 56376 .35 in 4
12
Ix =
c=
4.43
Peralte 65
=
= 32.5 in
2
2
Sx =
4.42
I x 56376 .1
=
= 1734 .65 in 3
c
32.5
M n = S x Fy = (1734.65)(36) = 62447.65i kips - in
4.5
2.5
M n = 5203 kips - ft
φ b M n = 0.90 (5203) = 4682 kips - ft < 4714 kips - ft (no satisfactoria)
2.2
1
Ensáyese una placa de patín de 1 in x 18 in (ver Figura 4.11).
2
Figura 4.11 Sección propuesta.
54
Capitulo IV
a) Fluencia al patín en tensión.
(1/ 4 )( 62 ) 3
+ 2(1.5 )(18 )(31 .75 ) 2 = 59400 .5 in 4
12
Ix =
Peralte 65
=
= 32.5 in
2
2
c=
Sx =
I x 59400 .5
=
= 1827.7 in 3
c
32.5
M n = S x Fy = (1827.7)(36) = 65797 kips - in
4.42
4.43
4.5
2.5
M n = 5483 kips - ft
φ b M n = 0.90 (5483) = 4934.77 kips - ft > 4714 kips - ft (satisfactorio)
2.2
b) Resistencia al pandeo lateral torsional PLT.
1
12
Iy =
(0.25 3 )(62)
6
A = (1.5)(18 ) +
rT =
λ=
+ 1.5(18 3 ) = 729 in 4
(62)(0.25 )
= 29.58 in 2
6
729
= 4.96 in 2
29.58
12(a1 ) 12(30 )
=
= 72.52
rT
4.96
λp =
300
λr =
756
Fy
Fy
=
=
300
36
756
36
= 50
= 126
4.6
4.7
4.8
2.7
2.8
2.9
55
Capitulo IV
Como λ > λ p
Cb =
12.5(M u )
2.5(M u ) + 3(M a ) + 4(M b ) + 3(M c )
Cb =
12.5( 4714 )
= 1.49
2.5( 4714 ) + 3(1538 ) + 4(2837 ) + 3(3896 )
⎡ 1 ⎛ λ − λp
Fcr = C b Fy ⎢1 − ⎜
⎜
⎣⎢ 2 ⎝ λr − λ p
⎞⎤
⎟⎥
⎟
⎠⎦⎥
4.44
2.11
⎡
⎛ 72.52 − 50 ⎞⎤
Fcr = (1.49 )(36 )⎢1 − 0.5⎜
⎟⎥ = 45.82 ksi
⎝ 126 − 50 ⎠⎦
⎣
4.9
Aw
15.5
=
= 0 .6
Af
25.58
ar =
R PG = 1 −
= 1−
ar
1200 + 300ar
⎛ h 970 ⎞
⎟
⎜ −
⎟
⎜ tw
F
cr ⎠
⎝
4.10
0. 6
970 ⎞
⎛
⎜ 248 −
⎟ = 0.954
1200 + 300(0.6) ⎝
36 ⎠
M n = Fcr R PG S x = (45.82)(0.954 )(1827 .7) = 79909 .4 kips - in = 6659 kips - ft
2.6
φ b M n = 0.90 (6659) = 5993.1 kips - ft > 4715.9 kips - ft (satisfactorio)
2.2
c) Resistencia al pandeo local PLP.
Kc =
4
4
=
== 0.254
62
h
tw
0.25
2.16
0.35 ≤ K c < 0.763 , entonces K c = 0.35
λ=
bf
18
=
=6
2t f 2(1.5)
λp =
65
Fy
=
65
36
= 10.83
2.13
2.14
56
Capitulo IV
Como λ < λ p
Fcr = Fy = 36 ksi
2.17
4.45
Af = bf t f
Af = 18(1.5) = 27 in 2
ar =
Aw 15.5
=
= 0.574
27
Af
R PG
ar
= 1−
1200 + 300ar
= 1−
⎛ h 970 ⎞
⎜ −
⎟
⎜ tw
⎟
F
cr ⎠
⎝
4.9
4.10
⎛
0 .6
970 ⎞
⎜⎜ 248 −
⎟⎟ = 0.9639
1200 + 300(0.57) ⎝
36 ⎠
M n = Fcr R PG S x = (36)(0.963)(1827 .7) = 63430 kips - in = 5286 kips - ft
2.6
φ b M n = 0.90 (5286) = 4757 kips - ft > 4749 kips - ft (satisfactorio)
2.2
Revísese la resistencia por cortante. La fuerza cortante es máxima en los
apoyos, pero la acción del campo de tensión no puede usarse en un tablero de
extremo. La separación de los atiesadores se determinan como sigue:
•
Primera sección y segunda sección:
a) Se iguala la resistencia requerida por cortante a la resistencia por cortante
dada por la ecuación 3.1 ó 3.6, y se despeja el valor de Cv .
Cv =
Vn
223
=
= 0.734
(0.9) (0.6)(15.5)(36)
0.9 0.6 A w Fy
(
)
3.6
b) Se despeja K v de la ecuación 3.4 o 3.5, se obtiene la ecuación 4.46.
2
Cv ⎛⎜ h ⎞⎟ FY
t
(0.734 )(248 )2 (36) = 36.94
Kv = ⎝ w ⎠
=
44000
44000
4.46
57
Capitulo IV
c) Despeje el valor requerido de
5
a=h
Kv
5
a
de la ecuación 4.12.
h
4.47
= 24.53 in
Se usará una separación del primer atiesador a = 20 in
Se obtendrá la separación de los atiesadores intermedios con la resistencia
requerida por cortante fuera de los tableros extremos.
Se introduce el factor de reducción:
4.48
⎛ 25 ⎞
⎛ a ⎞
221 − w ⎜ ⎟ 221 − 4.26⎜ ⎟
⎝ 12 ⎠ = 235.9 kips
⎝ 12 ⎠ =
Vn =
0 .9
0 .9
Para los tableros extremos de trabes armadas no híbridas con acción de
campo de tensión se tiene que: a = 56 in
4.12
⎛
⎞
⎜ 5 ⎟
Kv = 5 + ⎜
= 11.12
2 ⎟
⎜a
⎟
⎝ h ⎠
( )
Cv =
44000K v
2
⎛h ⎞ F
⎜ t ⎟ y
⎝ w⎠
Como
=
44000 ⋅ 11.12
(62 0.25) 36
h
K
> 187 v
Fy
tw
2
3.5
= 0.22
⎡
⎛ 1 0.22
Vn = (0.6 )(15.5 )(36 )⎢0.22 + ⎜⎜
2
⎢⎣
⎝ 1.15 1 + .9
⎞⎤
⎟⎥
⎟
⎠⎥⎦
3.3
= 242.31 kips > 235.9 kips
(satisfactorio)
Se usará una separación de atiesadores intermedios a = 56 in (Figura 4.12)
58
Capitulo IV
Figura 4.12 Separación de atiesadores.
Se diseñará las dimensiones de los atiesadores intermedios
J=
2. 5
=
2 .5
(a h) (a h)
2
2
3.20
= 13.37
El momento de inercia requerido esta dado por la ecuación 3.19:
I st = at w3 j = 56(0.25) 3 (13.37) = 11.7 in 4
3.19
Usando un valor máximo de
b
, se calcula “b” con la ecuación 4.49.
t
Después se despeja “t” de la ecuación 3.16.
b=
t=
bf − t w 18 − 0.25
=
= 8.87 in
2
2
4.49
b
4.50
95
Fy
= 0.56 in
Ast = 2bt = 2(8.87)(0.56) = 9.95 in 2
4.51
Para 2 atiesadores:
I st 2
2
⎡ tb 2
tw ⎞ ⎤
⎛
=⎢
+ tb⎜ Ast + ⎟ ⎥ 2
2 ⎠ ⎥⎦
⎝
⎢⎣ 12
I st 2
2
⎡ 0.56(8.87) 2
tw ⎞ ⎤
⎛
=⎢
+ (0.56)(8.87)⎜ 9.95 + ⎟ ⎥ 2 = 1075 in 4
12
2 ⎠ ⎥⎦
⎝
⎣⎢
4.52
59
Capitulo IV
I st 2 > I st (satisfactorio)
Para determinar la longitud de los atiesadores, se calcula primero la
distancia entre la soldadura del atiesador y la soldadura del alma al patín. Las
Especificaciones del AISC indican una distancia mínima de 4t w y máxima de 6t w ,
por lo cual se utilizará una distancia de 5t w .
La = h - ( 5t w − t w ) = 60.5 in
Se usaran dos placas de
4.53
9
in × 9 in × 60.5 in para los atiesadores intermedios (ver
16
Figura 4.13.).
Figura 4.13 Atiesadores intermedios.
Los atiesadores de apoyo serán instalados en los soportes y debajo de
cada carga concentrada, su diseño se realizará siguiendo las ecuaciones 4.54 y
4.55.
b=
bf
18
−2=
− 2 = 7 in
2
2
4.54
60
Capitulo IV
t≥
b Fy
95
=
4.55
7 36
= 0.44 in
95
Ensáyese un atiesador con b = 7 in y t =
7
in
16
Se tienen las dimensiones del atiesador, se revisará su resistencia por
aplastamiento.
φR n = 0.75(1.8Fy Apb ) = 0.75(1.8)(36)(0.44)(7 − 0.5) × 2
= 279.3 kips > 223 kips
4.22
(satisfactorio)
Revísese el atiesador como una columna.
4.23
A = 2bt + 12t w = 6.9 in 2
I x = 188 in 4
r =
λc =
4.25
I
188
=
= 5.2 in
A
6 .9
0.75h
πr Fy 29000
Como λc < 1.5
4.27
= 0. 1
4.56
Fcr = 0.658 λ2c Fy = 35.84 ksi
φc Pn = φ c Fcr A = 0.85(35.84)(6.93) = 211 kips < 223 kips (no satisfactorio)
Deben aumentarse las dimensiones del atiesador. b = 7 in y t =
A = 2bt + 12tw = 2(7)(0.56 ) + 12(0.25 ) = 8.68 in2
4.29
9
in
16
4.23
61
Capitulo IV
I x = 241.2 in 4
r=
I
241.2
=
= 5.26 in
A
8.68
4.25
λc =
0.75h
= 0.0989
πr Fy 29000
4.27
Como λc < 1.5
Fcr = 0.658λc2 Fy = 35.85 ksi
φc Pn = φ c Fcr A = 0.85(35.8)(8.68 ) = 264.8 kips > 223 kips (satisfactorio)
Se usarán placas de
4.56
4.29
9
in × 7in para los atiesadores de apoyo (ver Figura 4.14).
16
Figura 4.14 Atiesadores de apoyo.
Se han dimensionado todas las componentes de la trabe armada. Las
conexiones de esos elementos serán diseñadas, se utilizarán para todas las
soldaduras electrodos E60 con una resistencia de diseño de φFw = 27 ksi .
a) Calcúlese la separación de la soldadura entre el alma y el patín.
G=
peralte t f
− = 31.75 in
2
2
4.57
62
Capitulo IV
Q = Af G = (18 )(1.5)(27 ) = 729
I xx =
4.58
4.59
tw h 3
+ 2(bf t f G 2 ) = 59400 .5 in 4
12
Máximo =
4.60
223(729 )
kips
= 2.73
59400
in
Para los espesores de placa por soldar se usará un tamaño de soldadura
de w = t w . La longitud mínima de soldadura se calcula con la ecuación 4.61.
Lmin = 4(w ) ≥ 1.5 in
4.61
Lmin = 4(0.25 ) = 1 in Usaremos 1.5 in
Ensáyese con dos soldaduras de filete de 0.25 in × 1.5 in .
La capacidad por pulgada para 2 soldaduras se muestra en la ecuación
4.62.
Capacidad = 2(0.707w φFw )
= 2(0.707 )(0.25 )(27 ) = 9.5
4.62
kips
in
La capacidad por cortante del metal base se obtiene con la ecuación 4.63.
t (φFBM ) = t w [(0.9(0.60Fy ))] = 0.25(0.54)(36) = 4.86
kips
in
4.63
Empléese una capacidad total de soldadura de 4.86 kips/in. La capacidad
de un par de soldaduras de 1.5 in se calcula con la ecuación 4.64.
[
]
Lsoldadura t w (0.9(0.60Fy )) = 4.86(1.5) = 7.29 kips
4.64
Para determinar la separación de las soldaduras en pulgadas se resuelve la
ecuación 4.65.
63
Capitulo IV
7.29
s=
VuQ
Ix
=
7.29
= 2.67 in < 12 in (satisfactorio)
2.73
4.65
Aunque la separación de s = 2.67 in centro a centro se utiliza para toda la
longitud de la trabe, una mayor separación puede usarse donde la fuerza cortante
es menor que la máxima. Se determinará una separación de 5 pulgadas (ver
ecuación 4.66).
Vu 2 =
7.29I xx 7.29(59400 )
=
= 118 kips
Q (s )
729(5 in)
4.66
Refiérase a la Figura 4.9 y sea “x” la distancia desde el soporte izquierdo
(ver ecuación 4.67.).
x=
223 − 118
= 24.19 ft
4.34
4.67
Figura 4.15 Separación de soldadura Alma-Patín.
b) Calcúlese la soldadura de los atiesadores intermedios.
Tamaño mínimo de soldadura = t w =
1
in
4
4.68
64
Capitulo IV
Longuitud mínima = 4t w = 1 in < 1.5 in Usaremos 1.5 in
f = 0.045h
Fy3
E
= 0.045(62)
(36 )3
kips
= 3.53
29000
in
4.69
3.21
La separación máxima permisible de la soldadura se calcula con la
ecuación 4.70.
16t w = 16(0.25 ) = 4in
s=
4.70
7.29
= 2.06 in < 5 in (satisfactorio)
3.53
Se usará soldadura de filete de
4.71
1
in × 1.5 in para los atiesadores intermedios.
4
c) Calcúlese la soldadura de los atiesadores de apoyo:
Longuitud mínima = 4t w = 4(0.25 ) = 1 in < 1.5 in Usaremos 1.5in.
4.69
Tamaño mínimo = t w = 0.25 in
4.68
Re acción
223
kips
=
= 3.65
Longuitud disponible para soldadura 62 − 1.5
in
4.72
s=
7.29
= 1.99 in
3.65
4.73
Se usará soldadura de filete de 0.25 i n × 1.5 in para los atiesadores de apoyo.
65
Capitulo IV
4.1.3. EJEMPLO 3
Diseñe una trabe armada simplemente apoyada con un claro de 60 pies
que debe soportar las cargas de servicio que se muestran en la Figura 4.16.
Considere acero A36 y electrodos E60xx. Suponga que la trabe tiene un soporte
lateral continuo.
Figura 4.16 Cargas de servicio.
•
Solución
Las cargas factorizadas, excluido el peso de la trabe, se muestran en la
Figura 4.17.
W = 1.2(2) + 1.6(1.75) = 5.2 klb/ft
4.30
P1 = 1.2(100 ) + 1.6(80) = 248 klb
4.31
Determínese el peralte general:
Longuitud del claro 60(12)
=
= 65.45 in
11
11
4.32
Se usará un peralte de 65in, un espesor t f de 1.5 in. y una altura de alma
dada por la ecuación 4.33.
66
Capitulo IV
h = 65 - 2(1.5) = 62 in
4.33
Figura 4.17 Cargas factorizadas y diagramas Cortante-Momento.
Para determinar el espesor del alma, examine primero los valores límite de
h
. Para que este miembro a flexión califique como trabe armada, debe
tw
satisfacerse la ecuación 2.1.
970
970
h
≥
=
= 161.7
tw
36
Fyf
tw ≤
h
62
=
= 0.383 in
161.7 161.7
2.1
4.34
67
Capitulo IV
Para
tw ≥
Para
tw ≥
h 2000 2000
≤
=
= 333.3
tw
36
Fyf
a
≤ 1 .5
h
4.35
62
= 0.186 in
333.3
a
> 1 .5
h
14,000
14,000
h
≤
=
= 322.0
tw
36(36 + 16.5)
Fyf (Fyf + 16.5 )
2.21
4.36
62
= 0.192 in
322.0
Ensáyese una placa de alma de
2.20
1
in x 62 in .
4
Determínese el tamaño requerido de patín.
A w = 62 (1 4) = 15.5 in 2
Af =
Mu
A
5389(12)
62(1/ 4)
− w =
−
= 29.6 in 2
0.90hFy
6
0.90(62)(36 )
6
4.37
4.38
Con la ecuación 4.40 se puede estimar el peso de la trabe.
Total = 62 ( 1 4) + 2 (29.6) = 74.7 in2
Peso =
3.2(74.7)
klb
= 0.254
1000
ft
4.39
4.40
El momento flexionante ajustado se muestra en la Figura 4.18:
Mu = 5488.25 ft - kips
El área requerida para un patín es
Af =
Mu
A
5488(12)
62(1/ 4)
− w =
−
= 30.2 in 2
0.90hFy
6
0.90(62)(36 )
6
4.38
68
Capitulo IV
Figura 4.18 Cargas factorizadas con peso propio.
bf =
Af 30.2
=
= 20.13 in Redondeamos a 21 in
tf
1 .5
4.41
1
Ensáyese dos placas de patín de 1 in x 21 in
2
1
Supóngase con dos placa de patín de 1 in x 21 in y con una placa de alma de
2
1
in x 62 in .
4
69
Capitulo IV
Figura 4.19 Sección propuesta.
Revísese la resistencia a la flexión de la trabe armada:
a) Fluencia del patín en tensión.
(1/ 4 )( 62 ) 3
+ 2(1.5 )( 21)(31 .75 ) 2 = 68473 .1 in 4
12
4.42
Peralte 65
=
= 32.5 in
2
2
4.43
Ix =
c=
Sx =
I x 68473 .1
=
= 2106 in 3
c
32.5
M n = S x Fy = (2106 )(36) = 75847 i kips - in
4.5
2.5
M n = 6320 kips - ft
φ b M n = 0.90 (6320) = 5688 kips - ft > 5488 kips - ft (satisfactorio)
2.2
b) Resistencia al pandeo lateral torsional PLT.
70
Capitulo IV
(0.25 3 )(62)
1
Iy =
12
6
a = (1.5)(21) +
(62)(0.25)
= 34 in 2
6
300
λr =
756
Fy
Fy
=
=
300
36
756
36
2.8
= 50
2.9
= 126
Como λ < λ p
Fcr = Fy = 36 ksi
R PG = 1 −
= 1−
ar
1200 + 300ar
2.10
4.9
Aw 15.5
=
= 0.51
Af
30.2
ar =
4.7
2.7
12(a1 ) 12(20)
=
= 41.2
5.82
rT
λp =
4.6
4.8
1157 .6
= 5.82 in
34
rT =
λ=
+ 1.5(213 ) = 1157 .6 in 4
⎛ h 970 ⎞
⎜ −
⎟
⎜ tw
⎟
F
cr ⎠
⎝
4.10
⎛
0.51
970 ⎞
⎜⎜ 248 −
⎟⎟ = 0.967
1200 + 300(0.51) ⎝
36 ⎠
M n = Fcr R PG S x = (36)(0.967 )(2106 ) = 73365 kips - in = 6113.7 kips - ft
2.6
φ b M n = 0.90 (6113.7) = 5500 kips - ft > 5488 kips - ft (satisfactorio)
2.2
c) Resistencia al pandeo local PLP.
Kc =
4
4
=
= 0.254
62
h
tw
0.25
2.16
0.35 ≤ K c < 0.763 , entonces K c = 0.35
71
Capitulo IV
λ=
2.13
bf
21
=
=7
2t f 2(1.5)
λp =
65
F yf
=
65
36
Como λ < λ p
ar =
2.14
= 10.83
Fcr = Fy = 36 ksi
4.9
Aw 15.5
=
= 0.51
30.2
Af
R PG = 1 −
= 1−
ar
1200 + 300ar
2.17
⎛ h 970 ⎞
⎜ −
⎟
⎜ tw
Fcr ⎟⎠
⎝
4.10
⎛
0.51
970 ⎞
⎜⎜ 248 −
⎟⎟ = 0.967
1200 + 300(0.51) ⎝
36 ⎠
M n = Fcr R PG S x = (36 )(0.967 )(2106 ) = 73365 kips - i n = 6113.7 kips - ft
2.6
φ b M n = 0.90 (6113.7) = 5500 kips - ft > 5488 kips - ft (satisfactorio)
2.2
Se usará dos placas de patín de 1 21 in x 21 in
Revisamos ahora la resistencia por cortante. La fuerza cortante es máxima
en los apoyos, pero la acción del campo de tensión no puede usarse en un tablero
de extremo. La separación de los atiesadores se determina como sigue:
•
Primera sección
a) Se iguala la resistencia requerida por cortante a la resistencia por cortante
dada por la ecuación 3.1 ó 3.6, se despeja el valor de Cv .
Cv =
328
Vn
=
= 1.09
0.9 (0.6 A w F)y (0.9) (0.6)(15.5)(36)
3.6
b) Se obtiene K v de la ecuación 4.46.
72
Capitulo IV
4.46
2
Cv ⎛⎜ h ⎞⎟ FY
2
1.09 ⋅ (248 ) ⋅ 36
⎝ tw ⎠
=
= 54.93
Kv =
44000
44000
c) SeObtiene “a” de la ecuación 4.47.
5
a=h
Kv
5
4.47
= 19.62 in Redondeamos a = 20 in
Se obtendrá la separación de los atiesadores intermedios con la resistencia
requerida por cortante de Vn = 319 kips fuera de los tableros extremos.
4.48
⎛ 20 ⎞
⎛ a ⎞
319 − w ⎜ ⎟ 319 − 5.45⎜ ⎟
⎝ 12 ⎠ = 355 kips
⎝ 12 ⎠ =
Vn =
0 .9
0. 9
Para los tableros extremos de trabes armadas no híbridas con acción de
campo de tensión se tiene que: a = 17 in
Kv = 5 +
Cv =
5
(a h)
2
44000K v
2
⎛h ⎞ F
⎜ t ⎟ y
⎝ w⎠
Como
4.12
= 71.5
=
44000 (71.5 )
(62.25) 36
Kv
h
≤ 187
tw
Fy
2
3.5
= 1.42
Vn = 0.6 Aw Fy = 0.6(15.5)(36 )
= 334.8 kips < 355 kips
(no satisfactorio)
3.2
Es la máxima capacidad que puede resistir esta trabe al cortante, incluso aunque
se disminuyera el valor de “ a ”, la resistencia Vn no cambia. Lo único que queda
por hacer es aumentar la dimensión de t w para que resista el cortante.
Se intentará con un valor de t w = 0.3125 in (ver Figura 4.20).
73
Capitulo IV
Figura 4.20 Sección propuesta.
Aw = ht w = 62(0.3125 ) = 19.3 in
a) Cv =
328
Vn
=
= 0.873
(0.9 ) (0.6)(19.3)(36)
0.9 0.6 A w Fy
(
)
2
Cv ⎛⎜ h ⎞⎟ FY
2
.873 ⋅ (198.4 ) ⋅ 36
⎝ tw ⎠
b) K v =
=
= 28.12
44000
44000
c) a = h
5
5
Kv
= 29 in
4.37
3.6
4.46
4.47
Se usará una separación centro a centro del primer atiesador a = 35 in
Para los tableros extremos de trabes armadas no híbridas con acción de
campo de tensión se tiene que: a = 42 in
Kv = 5 +
5
(a h)
2
= 15.89
4.12
74
Capitulo IV
Cv =
44000K v
2
⎛h ⎞ F
⎜ t ⎟ y
⎝ w⎠
Como
=
44000 15.89
(62 0.312) 36
2
3.5
= 0.49
⎡
⎢
1 Cv
Vn = 0.6 Aw Fy ⎢Cv +
⎢
1.15 1 + a
h
⎣
= 359 kips > 355 kips
Kv
h
> 187
tw
Fy
( )
2
⎤
⎥
⎥ (satisfactorio)
⎥
⎦
3.3
Se usará una separación centro a centro de atiesadores intermedios a = 42 in
•
Segunda sección
Análisis de la resistencia al cortante de la otra sección de la trabe:
a) Cv =
246.2
Vn
=
= 0.65
(0.9) (0.6)(19.3)(36)
0.9 0.6 A w Fy
(
)
3.6
2
Cv ⎛⎜ h ⎞⎟ FY
2
tw ⎠
(
0.65 )(198.4 ) (36 )
⎝
b) K v =
=
= 21.05
44000
44000
c) a = h
5
5
Kv
= 35 in
4.46
4.47
Se usará una separación centro a centro del primer atiesador a = 35 in
Para los tableros extremos de trabes armadas no híbridas con acción de
campo de tensión tenemos que: a = 89 in
Kv = 5 +
5
( h)
a
2
= 7.42
4.12
75
Capitulo IV
Cv =
44000K v
h
Como
2
tw
=
Fy
h
> 187
tw
44000(7.42)
= 0.23
2
62
0.312 36
(
Kv
Fy
3.5
)
⎡
⎢
1 − Cv
Vn = 0.6 Aw Fy ⎢Cv +
⎢
1.15 1 + a
h
⎣
= 256 kips > 255 kips
( )
2
⎤
⎥
⎥ (satisfactorio)
⎥
⎦
3.3
Se usará una separación centro a centro de atiesadores intermedios a = 89 in
Figura 4.21 Atiesadores.
Diseño de las dimensiones de los atiesadores intermedios
J=
2. 5
=
2 .5
(a h) (a h)
2
2
3.20
= 9.42
3.19
I st = at w3 j = 42(.312) 3 (9.42) = 12 in 4
Usando un valor máximo de
b
, se calcula “b” con la ecuación 4.49.
t
Después se despeja “t” de la ecuación 3.16.
b=
t=
bf − t w 21 − 0.312
=
= 10.34 in
2
2
4.49
b
4.50
95
Fy
= 0.65 in
76
Capitulo IV
Ast = 2bt = (2)(10.34)(0.65) = 13.51 in2
4.51
Para 2 atiesadores:
Ist 2 =
0.65(10.34 )2
2
+ (0.65)(10.34 )(13.51+ tw 2) x 2 = 2646 in4
12
4.52
I st 2 > I st (satisfactorio)
Para determinar la longitud de los atiesadores, se calcula primero la
distancia entre la soldadura del atiesador y la soldadura del alma al patín. Las
especificaciones del AISC indican una distancia mínima de 4t w y máxima de 6t w ,
por lo cual se usará una distancia de 5t w .
La = h - ( 5t w − t w ) = 60 in
Empléese dos placas de
4.53
3
in × 10 in × 60 in para los atiesadores intermedios (ver
4
Figura 4.22.).
Figura 4.22 Atiesadores intermedios.
77
Capitulo IV
Los atiesadores de apoyo serán instalados en los soportes y debajo de
cada carga concentrada. Su diseño se realizará siguiendo las ecuaciones 4.54 y
4.55.
b=
bf
21
−2=
− 2 = 8.39 in
2
2
4.54
b Fy
4.55
8.5 36
t≥
=
= 0.53 in
95
95
Revísese la resistencia por aplastamiento.
φR n = 0.75(1.8Fy Apb ) = 0.75(1.8)(36)(0.53)(8.5- 0.5) × 2
= 417.3 kips > 328.9 kips
(satisfactorio)
4.22
Revísese el atiesador como una columna.
4.23
A = 2bt + 12t w = 10.34 in 2
I x = 409.5 in 4
r=
4.25
I
409.5
=
= 6.3 in
A
10.34
0.75h
λc =
πr
Fy
4.27
= 0.082
29000
Como λc < 1.5
Fcr = 0.658 λ2c Fy = 35.8 ksi
φc Pn = φc Fcr A = 0.85(35.8)(10.34)
= 314.2 kips < 328.9 kips
(no satisfactorio)
4.56
4.29
Debe aumentarse las dimensiones del atiesador. b = 8.5 in y t = 1 in
A = 2bt + 12t w = 2(1)(8.5) + 12(.312) = 18.8 in 2
4.23
78
Capitulo IV
I x = 790.75 in 4
4.25
I
790.75
=
= 6.48 in
A
18.8
r=
λc =
0.75h
πr Fy 29000
4.27
= 0.080
Como λc < 1.5
Fcr = 0.658 λ2c Fy = 35.8 ksi
φc Pn = φc Fcr A = 0.85(35.8)(18.8) = 573.6 kips > 328.9 kips (satisfactorio)
4.56
4.29
Empléese dos placas de 1 in × 8.5 in para los atiesadores de apoyo (Figura 4.23.)
Figura 4.23 Atiesadores de apoyo.
Se han dimensionado todas las componentes de la trabe armada. Las
conexiones de esos elementos serán ahora diseñadas. Se utilizarán para todas las
soldaduras electrodos E60 con una resistencia de diseño de φFw = 27 ksi .
a) Calcúlese la separación de la soldadura entre el alma y el patín.
G=
peralte t f
- = 31.75 in
2
2
4.57
79
Capitulo IV
4.58
Q = área del patín × G = 21(1.5) × 31.75 = 1000 in 4
I xx
tw h 3
=
+ 2(bf t f G 2 ) = 69714 .4 in 4
12
4.59
kips
328.9(1000 )
= 4.71
in
69714 .4
4.60
Máximo =
Para los espesores de placa por soldar se usará un tamaño de soldadura
de w = t w . La longitud mínima de soldadura se muestra en la ecuación 4.61.
Lmin = 4(w ) ≥ 1.5 in
4.61
Lmin = 4(0.312) = 1.25 in 2 Usaremos 1.5 in
Inténtese con soldaduras de filete de
1
5
in × 1 in
2
16
La ecuación 4.62 muestra la capacidad por pulgada para 2 soldaduras
Capacidad = 2(0.707W φFw )
= 2(0.707 )(0.312 )(27 ) = 11.91
4.62
kips
in
La capacidad por cortante del metal base se muestra en la ecuación 4.63.
[(
)]
t (φFBM ) = t w 0.9(0.60Fy ) = 0.312(0.54)(36) = 6.07
kips
in
4.63
La capacidad de un par de soldaduras de 1.5 in se calcula con la ecuación
4.64.
Lsoldadura t w [(0.9(0.60Fy ))] = 6.075(1.5) = 9.12 kips
4.64
Para determinar la separación de las soldaduras en pulgadas se resuelve la
ecuación 4.65.
80
Capitulo IV
9.12
s=
VuQ
Ix
=
9.12
= 1.93 in < 12 in (satisfactorio)
4.72
4.65
Aunque la separación de 1.93 pulgadas centro a centro se utiliza para toda
la longitud de la trabe, una mayor separación puede usarse donde la fuerza
cortante es menor que la máxima. Se determinará una separación de 5 pulgadas
(ver ecuación 4.66).
Vu 2 =
4.66
9.12(69714 )
= 127 kips
1000(5 in)
Refiérase a la Figura 4.18 y sea “x” la distancia desde el soporte derecho,
ver ecuación 4.67.
x=
246 − 118
= 23.7 ft
5 .4
4.67
Figura 4.24 Separación de soldadura Alma-Patín.
b) Calcúlese la soldadura en atiesadores intermedios.
Tamaño mínimo de soldadura =
3
in
16
4.68
81
Capitulo IV
⎛ 3 ⎞
Longuitud mínima = 4⎜ ⎟ = 0.75 in < 1.5 in Usaremos 1.5 in
⎝ 16 ⎠
Fy3
(36)3
kips
f = 0.045h
= 0.045(62)
= 3.53
29000
in
E
4.69
3.21
La separación máxima permisible de la soldadura es:
4.70
16t w = 16(0.312) = 5 in
s=
9.11
= 2.57 in < 5 in (satisfactorio)
3.53
Se usará soldadura de filete de
4.71
5
in × 1 21 in para los atiesadores intermedios.
16
c) Calcúlese la soldadura de los atiesadores de apoyo:
Longuitud mínima = 4t w = 4(0.312) = 1.25 in < 1.5 in
4.69
Usaremos 1.5 in
Tamaño mínimo = t w = 0.312 in
4.68
Re acción
328.9
kips
=
= 5.43
Longuitud disponible para soldadura 62 - 1.5
in
4.72
s=
9.11
= 1.67 in
5.43
Se usará soldadura de filete de
4.73
5
in × 1 21 in para los atiesadores de apoyo.
16
82
Capitulo IV
4.1.4. EJEMPLO 4
Diseñe una trabe armada simplemente apoyada con un claro de 50 pies
que debe soportar las cargas de servicio que se muestran en la Figura 4.25.
Considere acero A36 y electrodos E60xx. Suponga que la trabe tiene un soporte
lateral continuo.
Figura 4.25 Cargas de servicio.
•
Solución
Las cargas factorizadas, excluido el peso de la trabe, se muestran en la
Figura 4.26.
W = 1.2 (2) + 1.6 (2.5) = 6.4
klb
ft
4.30
P1 = 1.2 (30) + 1.6 (50) = 116 kips
4.31
P2 = 1.2 (30) + 1.6 (50) = 116 kips
4.31
Determínese el peralte general.
Longuitud del claro (12)50
=
= 55 in
11
11
4.32
83
Capitulo IV
Figura 4.26 Cargas factorizadas.
Considérese un peralte de 55 in y un espesor t f de patín de 1.5 in y una
altura de alma dada por la:
h = 55 - 2(1.5) = 52 in
4.33
Para determinar el espesor del alma, examine primero los valores límite de
h
. Para que este miembro a flexión califique como trabe armada debe
tw
satisfacerse la ecuación 2.1.
970 970
h
≥
=
= 161.7
tw
36
Fyf
2.1
84
Capitulo IV
Despejando t w de la ecuación 2.1, se obtiene la ecuación 4.34.
tw ≤
4.34
52
h
=
= 0.322 in
161.7 161.7
h 2000 2000
≤
=
= 333.3
tw
Fyf
36
Para
a
≤ 1. 5
h
. tw ≥
52
= 0.156 in
333.3
2.20
4.35
Para a h > 1.5, tenemos las ecuaciones 2.21 y 4.36.
Para
tw ≥
a
> 1. 5
h
h
14,000
14,000
≤
=
= 322.0
tw
Fyf (Fyf + 16.5)
36(36 + 16.5)
4.36
52
= 0.161 in
322.0
Ensáyese una placa de alma de
2.21
1
in x 52 in .
4
Determinación del tamaño requerido de patín.
A w = 52 ( 1 4) = 13 in 2
Af =
Mu
A
3740(12)
13
− w =
−
= 24.47 in 2
0.90hFy
6
0.90(52)(36 ) 6
4.37
4.38
Con la ecuación 4.40 se puede estimar el peso de la trabe.
Total = 52 ( 1 4) + 2 (24.47) = 61.94 in 2
4.39
3.4 ( 61.94)
klb
= 0 .211
1000
ft
4.40
Peso =
85
Capitulo IV
Figura 4.27 Cargas factorizadas con peso propio.
El momento flexionante ajustado se muestra en la Figura 4.27:
Mu = 3805.814 kips - ft
El área requerida para un patín se muestra en la ecuación 4.38.
Af =
Mu
A
3805 .814(12) 52(1/ 4)
− w =
−
= 24.94 in 2
0.90hFy
6
0.90(52)(36 )
6
4.38
bf =
Af 24.94
=
= 16.63 in 2
tf
1 .5
4.41
Redondeamos a 17 in
1
Inténtese dos placas de patín de 1 in x 17 in
2
86
Capitulo IV
1
Ensáyese con una placa de patín de 1 in x 17 in y con una placa de alma de
2
1
in x 52 in .
4
Figura 4.28 Sección propuesta.
Revisión de la resistencia a la flexión de la trabe armada:
a) Fluencia del patín en tensión.
Ix =
(1/ 4 )(52 )3
+ 2(1.5 )(17 )(715 .56 ) = 39423 in 4
12
4.42
c=
Peralte 55
=
= 27.5 in
2
2
4.43
Sx =
I x 39423
=
= 1433.56 in 3
c
27.5
Mn = S x Fy = (1433.56)(36) = 51608 .32 kips - in
4.5
2.5
Mn = 4300.69 kips - ft
87
Capitulo IV
φ b M n = 0.90 (4300.69) = 3870.62 kips - ft > 3805 .814 kips - ft (satisfactorio)
2.2
b) Resistencia al pandeo lateral torsional PLT.
(
)
⎤
1 ⎡ 0.25 3 (52 )
Iy =
+ 1.5 173 ⎥ = 614.14 in4
⎢
12 ⎣
6
⎦
A = (1.5)(17) +
4.6
(52)(0.25)
= 27.667 in 2
6
4.7
4.8
614.14
= 4.71 in
27.667
rT =
•
λ=
( )
Primera y tercera sección
2.7
12(a1 ) 12(15 )
=
= 38.2
4.71
rT
λp =
300 300
=
= 50
36
Fy
2.8
λr =
756 756
=
= 126
36
Fy
2.9
Como λ < λ p
ar =
Fcr = Fy = 36 ksi
Aw
13
=
= 0.52
Af
24.94
R PG = 1 −
ar
1200 + 300ar
= 1−
⎛ h 970 ⎞
⎜ −
⎟
⎜ tw
Fcr ⎟⎠
⎝
2.10
4.9
4.10
⎛
0.52
970 ⎞
⎜⎜ 208 −
⎟⎟ = 0.982
1200 + 300( 0.52 ) ⎝
36 ⎠
M n = Fcr R PG S x = (36)(0.982)(1433 .56) = 50689 .4 kips - in = 4224.1 kips - ft
2.6
φ b M n = 0.90 (4224.1) = 3801.71 f kips - ft > 3475 .28 kips - ft (satisfactorio)
2.2
88
Capitulo IV
•
λ=
Segunda sección
12(a 2 ) 12(20 )
=
= 50.94
4.71
rT
2.7
λp =
300 300
=
= 50
36
Fy
2.8
λr =
756 756
=
= 126
36
Fy
2.9
Como λ > λp
Cb =
12.5(M u )
2.5(M u ) + 3(M a ) + 4(M b ) + 3(M c )
4.44
12.5(3805.81)
2.5(3805.81) + 3(3723.18 ) + 4( 3805.81) + 3(3723.18 )
= 1.01
⎡
λ − λp ⎤
Fcr = C b Fy ⎢1 - 0.5
⎥ = 36.15 ksi
λr − λ p ⎦⎥
⎣⎢
ar =
Aw
13
=
= 0.52
Af
24.94
M n = Fcr R PG S x = (36.15)(0.982)(1433 .56)
2.11
4.9
2.6
= 50899 .66 kips - in = 4241.63 kips - ft
φ b M n = 0.90 (4241.63) = 3817.48 kips - ft > 3805 .814 kips - ft (satisfactorio)
2.2
c) Resistencia al pandeo local PLP.
Kc =
4
4
=
= 0.277
h
52
tw
0.25
2.16
0.35 ≤ K c < 0.763 , entonces K c = 0.35
λ=
bf
17
=
= 5.667
2t f 2(1.5)
2.13
89
Capitulo IV
λp =
2.14
65
65
=
= 10.83
Fy
36
Como λ < λ p
Fcr = Fy = 36 ksi
ar =
13
Aw
=
= 0.52
24.94
Af
RPG
ar
= 1−
1200 + 300ar
= 1−
2.17
4.9
⎛ h 970 ⎞
⎟
⎜ ⎟
⎜t
F
cr ⎠
⎝ w
4.10
0.52
970 ⎞
⎛
⎟ = 0.982
⎜ 208 −
1200 + 300(0.52) ⎝
36 ⎠
M n = Fcr R PG S x = (36)(0.982)(1433 .56) = 50689 .4 kips - in = 4224.12 kips - ft
2.6
φ b M n = 0.90 (4224.12) = 3801.71 kips - ft < 3805 .814 kips - ft (no satisfactorio)
2.2
1
Ensáyese una placa de patín de 1 in x 18 in y con una placa de alma de
2
1
in x 52 in , ver Figura 4.29.
4
Figura 4.29 Sección propuesta.
90
Capitulo IV
Figura 4.30 Cargas (peso propio incluido), diagrama Cortante-Momento.
M u = 3806 .811 kips - ft
Af = 24.95 in 2
Revisión de la resistencia a la flexión de la traba armada.
a) Fluencia de patín en tensión.
(1/ 4 )(52 ) 3
Ix =
+ 2(1.5 )(18 )(715 .56 ) = 41569 .71 in 4
12
c=
Peralte 55
=
= 27.5 in
2
2
Sx =
I x 41569 .71
=
= 1511.63 in 3
c
27.5
Mn = Sx Fy = (1511.63 )(36 ) = 54418 .53 kips - in
4.42
4.43
4.5
2.5
91
Capitulo IV
Mn = 54414 .53 kips - in = 4534.88 kips - ft
φ b M n = 0.90 (4534.88) = 4081.39 kips - ft > 3806 .811 kips - ft (satisfactorio)
2.2
b) Resistencia al pandeo lateral torsional PLT.
(
A = (1.5)(18) +
( )
4.6
(52)(0.25)
= 29.1667 in2
6
4.7
4.8
729.01
= 5 in
29.1667
rT =
•
λ=
)
⎤
1 ⎡ 0.253 (52 )
+ 1.5 183 ⎥ = 729.01 in4
⎢
12 ⎣
6
⎦
Iy =
Primera y tercera sección
2.7
12(a1 ) 12(15 )
=
= 36
5
rT
λp =
300 300
=
= 50
36
Fy
2.8
λr =
756 756
=
= 126
36
Fy
2.9
Como λ < λ p
ar =
Fcr = Fy = 36 ksi
13
Aw
=
= 0.52
24.95
Af
RPG = 1 = 1-
ar
1200 + 300ar
⎛ h 970 ⎞
⎟
⎜ ⎟
⎜t
F
cr ⎠
⎝ w
2.10
4.9
4.10
0.52
970 ⎞
⎛
⎟ = 0.982
⎜ 208 −
1200 + 300(0.52) ⎝
36 ⎠
M n = Fcr R PG S x = (36)(0.982)(1511 .63) = 53449 .82 kips - in = 4454.15 kips - ft
2.6
92
Capitulo IV
φ b M n = 0.90 (4454.15) = 4008.74 kips - ft > 3476 .12 kips - ft (satisfactorio)
•
λ=
2.2
Segunda sección
2.7
12(a2 ) 12(20 )
=
= 48
5
rT
λp =
300 300
=
= 50
36
Fy
2.8
λr =
756 756
=
= 126
36
Fy
2.9
Como λ < λp
Fcr = Fy = 36 ksi
13
Aw
=
= 0.52
24.95
Af
ar =
R PG = 1 −
= 1−
ar
1200 + 300ar
⎛ h 970 ⎞
⎜ −
⎟
⎜ tw
⎟
F
cr ⎠
⎝
2.10
4.9
4.10
⎛
0.52
970 ⎞
⎜⎜ 208 −
⎟⎟ = 0.982
1200 + 300(0.52) ⎝
36 ⎠
M n = Fcr R PG S x = (36)(0.982)(1511 .63) = 53449 .82 kips - i n = 4454.15 kips - ft
2.6
φ b M n = 0.90 (4454.15) = 4008.74 kips - ft > 3806 .811 kips - ft (satisfactorio)
2.2
c) Resistencia al pandeo local PLP.
Kc =
4
=
h
tw
4
= 0.277
52
0.25
2.16
0.35 ≤ K c < 0.763 , entonces K c = 0.35
λ=
18
bf
=
=6
2t f 2(1.5)
2.13
93
Capitulo IV
λp =
Como λ < λp
ar =
2.14
65
65
=
= 10.83
36
F yf
Fcr = Fy = 36 ksi
13
Aw
=
= 0.52
24.95
Af
R PG = 1 −
= 1−
ar
1200 + 300ar
⎛ h 970 ⎞
⎜ −
⎟
⎜ tw
⎟
F
cr ⎠
⎝
2.17
4.9
4.10
⎛
0.52
970 ⎞
⎜⎜ 208 −
⎟⎟ = 0.982
1200 + 300(0.52) ⎝
36 ⎠
M n = Fcr R PG S x = (36)(0.982)(1511 .63) = 53449 .82 kips - in = 4454.15 kips - ft
φ b M n = 0.90 (4454.15) = 4008.74 kips - ft > 3806 .811 kips - ft (satisfactorio)
2.6
2.2
Revísese ahora la resistencia por cortante. La fuerza cortante es máxima en
los apoyos, pero la acción del campo de tensión no puede usarse en un tablero de
extremo. La separación de los atiesadores se determinan como sigue:
•
Primera y tercera sección
a) Se Iguala la resistencia requerida por cortante a la resistencia por cortante
dada por la ecuación 3.1 ó 3.6 y se despeja el valor de Cv .
Cv =
Vn
281.34
=
= 1.11
0.9( 0.6 A wFy ) (0.9 )( 0.6 )(13 )(36 )
3.6
b) Se despeja K v de la ecuación 3.5.
2
Cv ⎛⎜ h ⎞⎟ FY
2
t
1.11⋅ (208 ) ⋅ 36
=
= 39.41
Kv = ⎝ w ⎠
44000
44000
4.46
c) Se calcula “a” de la ecuación 4.47.
94
Capitulo IV
5
a=h
5
Kv
4.47
= 19.82 in
Se usará una separación centro a centro de primer atiesador a = 20 in.
Se Obtendrá la separación de los atiesadores intermedios ahora con la
resistencia requerida por cortante de Vn = 281.34 kips fuera de los tableros
extremos.
⎛ a ⎞
⎛ 20 ⎞
281.34 − w ⎜ ⎟ 281.34 − 6.61⎜ ⎟
⎝ 12 ⎠ =
⎝ 12 ⎠ = 300.36 kips
Vn =
0.9
0.9
4.48
Para los tableros extremos de trabes armadas no híbridas con acción de
campo de tensión se tiene que: a = 160 in
4.12
⎛
⎞
⎜ 5 ⎟
Kv = 5 + ⎜
= 5.52
2 ⎟
⎜a
⎟
⎝ h ⎠
( )
Cv =
44000K v
⎛h
⎜⎜
⎝ tw
Como
2
⎞
⎟⎟ Fy
⎠
=
44000 (5.52 )
2
⎛ 52 ⎞
⎜
⎟ 36
⎝ 0.25 ⎠
h
K
> 234 v
tw
Fy
3.5
= 0.156
Vn = Aw
26400 k v
4.74
2
⎛h⎞
⎜⎜ ⎟⎟
(no satisfactorio)
t
⎝ w⎠
= 43.85 kips < 300 kips
Se intenta con a = 16 in
⎞
⎛
⎜ 5 ⎟
= 57.81
Kv = 5 + ⎜
2 ⎟
⎟
⎜a
⎝ h ⎠
4.12
( )
95
Capitulo IV
Como
K
h
< 187 v entonces,
tw
Fy
Vn = 0.6 Aw Fy = 280.8 kips < 300 kips (no satisfactorio)
3.2
La máxima capacidad que puede resistir esta trabe al cortante es Vn = 280.8 kips ,
incluso aunque se disminuyera el valor de “ a ”, la resistencia “Vn ” no cambia. Lo
único que queda por hacer es aumentar la dimensión de t w para que resista el
cortante.
1
Inténtese con una placa de patín de 1 in x 18 in y con una placa de alma de
2
5
in x 52 in , ver Figura 4.31.
16
Figura 4.31 Sección propuesta.
96
Capitulo IV
a) Cv =
3.6
Vn
281.34
=
= 0.89
0.9( 0.6 A wFy ) (0.9 )(0.6 )(16 )(0.25 )
4.46
2
⎛h⎞
Cv ⎜⎜ ⎟⎟ Fy
2
tw ⎠
(
0.89 )(166.4 ) (36 )
⎝
=
= 20.17
b) Kv =
44000
44000
c) a = h
4.47
5
= 30 in
Kv − 5
Para los tableros extremos de trabes armadas no híbridas con acción de
campo de tensión se tiene que: a = 38 in
4.12
⎞
⎛
⎜ 5 ⎟
= 14.36
Kv = 5 + ⎜
2 ⎟
a
⎟
⎜
⎝ h ⎠
( )
Cv =
44000K v
⎛h
⎜⎜
⎝ tw
Como
2
⎞
⎟⎟ Fy
⎠
=
44000 (14.36 )
2
⎛ 52 ⎞
⎜
⎟ 36
⎝ 0.312 ⎠
h
K
> 187 v
tw
Fy
3.5
= 0.63
⎡
⎢
1 Cv
Vn = 0.6 Aw Fy ⎢Cv +
2
⎢
1.15 1 + a
h
⎣
= 312.73 kips > 294.23 kips
( )
⎤
⎥
⎥ (satisfactorio)
⎥
⎦
3.3
Usaremos una separación centro a centro de atiesadores intermedios a = 38 in
•
Segunda sección
a = 240 in
⎞
⎛
⎜ 5 ⎟
= 5.23
Kv = 5 + ⎜
2 ⎟
⎟
⎜a
⎝ h ⎠
4.12
( )
97
Capitulo IV
Cv =
44000K v
2
⎛h ⎞ F
⎜ t ⎟ y
⎝ w⎠
Como
=
44000 ⋅ 5.23
(520.3125) 36
2
h
K
> 234 v
tw
Fy
Vn = Aw
3.5
= 0.23
26400K v
4.74
2
⎛h ⎞
(satisfactorio)
⎜ t ⎟
⎝ w⎠
= 81.10 kips > 66.13 kips
No se necesitan atiesadores intermedios en la segunda sección
Figura 4.32 Atiesadores.
Diseño de las dimensiones de los atiesadores intermedios
J=
2 .5
(a h)
2
−2 =
2. 5
(a h)
2
3.20
− 2 = 5.51
3.19
I st = at w3 j = 42(.312)3 (5.51) = 6.39 in 4
Usando un valor máximo de
b
, se calcula “b” con la ecuación 4.49.
t
Después se despeja “t” de la ecuación 3.16.
b=
t=
bf − tw 18 − 0.312
=
= 8.84 in
2
2
b
95
= 0.559 in
4.49
4.50
Fy
98
Capitulo IV
Ast = 2bt = (2)(8.84)(0.559) = 9.88 in 2
4.51
Para 2 atiesadores:
2
⎡ 0.56(8.84)2
t ⎞ ⎤
⎛
+ (0.56 )(8.84)⎜ 9.88 + w ⎟ ⎥ × 2 = 1059.39 in4
Ist 2 = ⎢
12
2 ⎠ ⎥⎦
⎝
⎢⎣
4.52
I st 2 > I st (satisfactorio)
Para determinar la longitud de los atiesadores, se calcula primero la
distancia entre la soldadura del atiesador y la soldadura del alma al patín. Las
Especificaciones del AISC indican una distancia mínima de 4tw y máxima de 6tw ,
por lo cual se utiliza una distancia de 5tw .
La = h - ( 5t w − t w ) = 50.125 in
Se usaran dos placas de
4.53
5
in × 9 in × 50.5 in para los atiesadores intermedios.
8
Figura 4.33 Atiesadores intermedios.
Los atiesadores de apoyo serán instalados en los soportes y debajo de
cada carga concentrada, su diseño se realizará de la siguiente manera:
99
Capitulo IV
b=
bf
18
−2 =
− 2 = 7 in
2
2
4.54
b Fy
4.55
7 36
=
= 0.44 in
t≥
95
95
Ensáyese una placa de atiesador. b = 7 in y t =
7
in
16
Se tienen las dimensiones del atiesador, se revisara la resistencia por
aplastamiento.
φR n = 0.75(1.8Fy Apb ) = 0.75(1.8)(36)(0.44)(7 − 0.5) × 2
= 279.32 kips < 281.34 kips
(no satisfactorio)
Debe aumentarse las dimensiones del atiesador. b = 7 in y t =
φRn = 0.75(1.8Fy Apb ) = 0.75(1.8)(36 )(0.57)(7-0.5) × 2
= 358.28 kips > 281.34 kips
(satisfactorio)
4.22
9
in
16
4.22
Revísese el atiesador como una columna.
4.23
A = 2bt + 12t w = 9.11 in 2
I x = 244.89 in 4
r=
4.25
I
244.89
=
= 5.18 in
A
9.11
λc =
πr
0.75h
Fy
4.27
= 0.0844
29000
Como λc < 1.5
Fcr = 0.658 λ2c Fy = 35.89 ksi
4.56
100
Capitulo IV
φc Pn = φc Fcr A = 0.85(35.89)(9.11) = 277.98 < 281.34 (No satisfactorio)
Debe aumentarse las dimensiones del atiesador. b = 7 in y t =
4.29
11
in
16
A = 2bt + 12t w = 2(0.69 )(7) + 12(.312) = 10.86 in 2
4.23
I x = 298.82 in 4
r=
I
298.82
=
= 5.25 in
A
10.86
4.25
λc =
0.75h
= 0.083
πr Fy 29000
4.27
Como λc < 1.5
Fcr = 0.658λ2c Fy = 35.9 ksi
φc Pn = φ c Fcr A = 0.85(35.9)(10.86 ) = 331.39 kips > 281.34 kips (satisfactorio)
Empléense dos placas de
4.56
4.29
11
in × 7 in en los atiesadores de apoyo (Figura 4.34).
16
Figura 4.34 Atiesadores de apoyo.
101
Capitulo IV
Se han dimensionado todas las componentes de la trabe armada. Las
conexiones de esos elementos serán diseñadas. Se utilizarán electrodos E60 con
una resistencia de diseño de φFw = 27 ksi .
a) Calcúlese la separación de la soldadura entre el alma y el patín.
G=
4.57
peralte t f
− = 26.75 in
2
2
Q = área del patín × G = 18(1.5) × 26.75 = 722.25 in 3
I xx
4.58
tw h 3
=
+ 2(bf t f G 2 ) = 42302 .04 in 4
12
4.59
281.34(722.25)
kips
= 4. 8
42302 .04
in
4.60
Maximo =
Para los espesores de placa por soldar usaremos un tamaño de soldadura
de w = tw . La longitud mínima de soldadura es:
4.61
Lmin = 4(w ) ≥1.5 in
Lmin = 4(.312 ) = 1.25 in Usaremos 1.5 in.
Ensayaremos con soldaduras de filete de 0.312 in × 1.5 in .
La capacidad por pulgada para 2 soldaduras se muestra en la ecuación
4.62.
Capacidad = 2(0.707w φFw )
= 2(0.707 )(0.312 )(27 ) = 11.91
4.62
kips
in
La capacidad por cortante del metal base es:
102
Capitulo IV
[
]
t (φFBM ) = tw (0.9(0.60Fy )) = 0.312(0.54 )(36) = 6.07
kips
in
4.63
La capacidad de un par de soldaduras de 1.5 in se calcula con la ecuación
4.64.
[
]
Lsoldadura t w (0.9(0.60Fy )) = 6.075(1.5) = 9.12 kips
4.64
Para determinar la separación de las soldaduras en pulgadas se resuelve la
ecuación 4.65.
s=
9.12 9.12
=
= 1.89 in < 12 in
VuQI x 4.80
(satisfactorio)
4.65
Aunque la separación s = 1.89 in 1.89 centro a centro se utiliza en toda la
longitud de la trabe, una mayor separación puede usarse donde la fuerza cortante
es menor que la máxima de 281 kips.
Vu 2 =
4.66
9.12( 42302 )
= 178 kips
722(3 in)
Refiérase a la Figura 4.27 y sea x la distancia desde el soporte izquierdo,
ver ecuación 4.67.
x=
281 − 178
= 15.6 ft
6. 6
4.67
b) Ahora calcularemos la separación de los atiesadores intermedios.
Tamaño mínimo de soldadura =
Longuitud mínima = 4
3
in
16
3
= 0.75 in < 1.5 in Usaremos 1.5 in
16
4.68
4.69
103
Capitulo IV
f = 0.045h
Fy3
(36 )3
kips
= 0.045(52)
= 2.97
E
29000
in
3.21
La separación máxima permisible de la soldadura es:
4.70
16t w = 16(0.312) = 5 in
s=
9.11
= 3.07 in < 5 in (satisfactorio)
2.97
4.71
Usaremos soldadura de filete de 0.312in. × 1.5in. para los atiesadores intermedios.
Figura 4.35 Soldadura Alma-Patín.
c) Ahora calcularemos la soldadura de los atiesadores de apoyo:
Longuitud mínima = 4t w = 4(0.312) = 1.25 in < 1.5 in Usaremos 1.5 in
4.69
Tamaño mínimo = t w = 0.312in.
4.68
Reacción
281.34
kips
=
= 5.57
Longuitud disponible para soldadura 52 - 1.5
in
4.72
104
Capitulo IV
s=
4.73
9.11
= 1.64 in
5.57
Usaremos soldadura de filete de
5
in × 1.5 in para los atiesadores de apoyo.
16
4.1.5. EJEMPLO 5
Diseñe una trabe armada simplemente apoyada con un claro de 50 pies
que debe soportar las cargas de servicio que se muestran en la Figura 4.36.
Considere acero A36 y electrodos E60xx. Suponga que la trabe tiene un soporte
lateral continuo.
Figura 4.36 Cargas de servicio.
•
Solución
Las cargas factorizadas, excluido el peso de la trabe, se muestran en la
Figura 4.37.
W = 1.2 (1.5) + 1.6 (2) = 5
klb
ft
4.30
P1 = 1.2 (20) + 1.6 (30) = 72 klb
4.31
P2 = 1.2 (10) + 1.6 (20) = 44 klb
4.31
105
Capitulo IV
Determinese el peralte general:
Longuitud del claro (12)50
=
= 55 in
11
11
4.32
Figura 4.37 Cargas factorizadas.
Se usará un peralte de 55in y un espesor t f de patín de 1.5 in y una altura
de alma dada por la ecuación 4.33.
h = 55 - 2(1.5) = 52 in
4.33
Para determinar el espesor del alma, examine primero los valores límite de
h
. Para que este miembro a flexión califique como trabe armada, debe cumplir
tw
con la ecuación 2.1.
106
Capitulo IV
2.1
970
970
h
≥
=
= 161.7
tw
36
Fyf
4.34
52
h
tw ≤
=
= 0.322 in
161.7 161.7
Para
tw ≥
Para
2.20
h 2000 2000
≤
=
= 333.3
tw
36
Fyf
a
≤ 1. 5
h
4.35
52
= 0.156 in
333.3
a
> 1 .5
h
h
≤
tw
14,000
Fy (Fy + 16.5)
=
14,000
36(36 + 16.5)
= 322.0
4.36
52
tw ≥
= 0.161 in
322.0
Ensáyese una placa de alma de
2.21
1
in x 52 in .
4
Se calcula el tamaño requerido de patín.
A w = 52 ( 1 4) = 13 in 2
Af =
Mu
A
2338.875(12) 13
− w =
−
= 14.49 in 2
0.90hFy
6
0.90(52)(36 )
6
4.37
4.38
Total = 52 ( 1 4) + 2 (14.49) = 41.98 in 2
4.39
3.4 ( 41.98)
klb
= 0.143
1000
ft
4.40
Peso =
El momento flexionante ajustado se muestra en la Figura 4.38:
Mu = 2383.04 kips - ft
107
Capitulo IV
Figura 4.38 Cargas factorizadas con peso propio.
El área requerida para un patín es:
Af =
Mu
A
2383 .07(12) 52(1/ 4)
− w =
−
= 14.81 in 2
0.90hFy
6
0.90(52)(36 )
6
4.38
bf =
Af 14.81
=
= 9.87 in
tf
1 .5
4.41
bf = 9.87 <
peralte
= 13.75 in Redondeamos a 14 in.
4
4.75
1
Inténtese una placa de patín de 1 in x 14 in y con una placa de alma de
2
1
in x 52 in .
4
108
Capitulo IV
Revisión de la resistencia a la flexión de la traba armada:
a) Fluencia al patín a tensión.
Ix =
(1/ 4 )(52 )3
+ 2(1.5 )(14 )(715 .56 ) = 32982 .96 in 4
12
4.42
c=
Peralte 55
=
= 27.5 in
2
2
4.43
Sx =
I x 32982 .96
=
= 1199.38 in 3
27.5
c
Mn = Sx Fy = (1199.38 )(36 ) = 43177 .69 kips - in
4.5
2.5
Mn = 3598 .14 kips - ft
φ b M n = 0.90 (3598.14) = 3238.33 kips - ft > 2383.07 kips - ft (satisfactorio)
2.2
Figura 4.39 Sección propuesta.
109
Capitulo IV
b) Resistencia al pandeo lateral torsional PLT.
(
)
⎤
1 ⎡ 0.253 (52 )
Iy =
+ 1.5 143 ⎥ = 343.01 in4
⎢
12 ⎣
6
⎦
a = (1.5)(14) +
4.6
(52)(0.25)
= 23.1667 in2
6
4.7
4.8
343.01
= 3.85 in
23.1667
rT =
•
λ=
( )
Primera sección
2.7
12(a1 ) 12(15 )
=
= 46.78
3.85
rT
λp =
300 300
=
= 50
36
Fy
2.8
λr =
756 756
=
= 126
36
Fy
2.9
Como λ < λ p
ar =
Fcr = Fy = 36 ksi
Aw
13
=
= 0.878
14.81
Af
RPG = 1 −
ar
1200 + 300ar
= 1−
⎛ h 970 ⎞
⎜ ⎟
⎜ tw
⎟
F
cr ⎠
⎝
2.10
4.9
4.10
0.878
970 ⎞
⎛
⎟ = 0.972
⎜ 208 −
1200 + 300( 0.878 ) ⎝
36 ⎠
M n = Fcr R PG S x = (36)(0.972)(1199.38) = 41977 .42 kips - in = 3498 .12 kips - ft
2.6
φ b M n = 0.90 (3498.12) = 3148.31 kips - ft > 2237 .97 kips - ft (satisfactorio)
2.2
•
Segunda sección
110
Capitulo IV
12(a2 ) 12(25 )
=
= 77.96
3.85
rT
λ=
2.7
λp =
300 300
=
= 50
36
Fy
2.8
λr =
756 756
=
= 126
36
Fy
2.9
Como λ > λ p
Cb =
Cb =
12.5(M u )
2.5(M u ) + 3(M a ) + 4(M b ) + 3(M c )
12.5(2383.04 )
2.5(2383.04 ) + 3(2378.95 ) + 4( 2319.04 ) + 3(2058.24 )
= 1.04
⎡
λ - λp ⎤
Fcr = Cb Fy ⎢1 - 0.5
⎥ = 30.66 ksi
λr - λp ⎥⎦
⎢⎣
⎛ h 970 ⎞
⎜ ⎟
⎜ tw
Fcr ⎟⎠
⎝
⎛
970 ⎞
0.878
⎜⎜ 208 −
⎟⎟ = 0.98
= 1−
1200 + 300(0.878 ) ⎝
30.66 ⎠
R PG = 1 −
4.44
ar
1200 + 300a r
M n = Fcr R PG S x = (30.96)(0.98)(1199 .38) = 36044 .03 kips - in
2.11
4.10
2.6
M n = 3003 .67 kips - ft
φ b M n = 0.90 (3003.67) = 2703.30 kips - ft > 2383.04 kips - ft (satisfactorio)
•
λ=
Tercera sección
12(a1 ) 12(10 )
=
= 31.19
3.85
rT
λp =
2.2
300 300
=
= 50
36
Fy
2.7
2.8
111
Capitulo IV
λr =
2.9
756 756
=
= 126
36
Fy
Como λ < λ p
RPG = 1 −
= 1−
Fcr = Fy = 36 ksi
ar
1200 + 300ar
⎛ h 970 ⎞
⎜ ⎟
⎜ tw
⎟
F
cr ⎠
⎝
2.10
4.10
0.878
970 ⎞
⎛
⎜ 208 −
⎟ = 0.972
1200 + 300(0.878) ⎝
36 ⎠
M n = Fcr R PG S x = (36)(0.972)(1199 .38) = 41977 .42 kips - in
2.6
M n = 3498 .12 kips - ft
φ b M n = 0.90 (3498.12) = 3148.31 kips - ft > 1596.55 kips - ft (satisfactorio)
2.2
c) Resistencia al pandeo local PLP.
4
Kc =
h
4
=
52
tw
= 0.277
2.16
0.25
0.35 ≤ K c < 0.763 , entonces K c = 0.35
λ =
λp =
bf
2t f
=
65
F yf
12
2(1.5 )
=
65
36
2.14
= 10.83
Como λ < λ p
R PG
2.13
= 4.667
Fcr = Fy = 36 ksi
⎛ h 970 ⎞
⎜ ⎟
⎜ tw
⎟
F
cr ⎠
⎝
⎛
0.878
970 ⎞
⎜⎜ 208 −
⎟⎟ = 0.972
= 1−
1200 + 300(0.878 ) ⎝
36 ⎠
ar
= 1−
1200 + 300a r
2.17
4.10
112
Capitulo IV
M n = Fcr R PG S x = (36)(0.972)(1199 .38) = 41977 .42 kips - in
2.6
M n = 3498 .12 kips - ft
φ b M n = 0.90 (3498.12) = 3148.31 kips - ft > 2383.04 kips - ft (satisfactorio)
2.2
1
1
Se usarán dos placa de patín de 1 in x 14 in y una placa de alma de in x 52 in .
2
4
Revísese la resistencia por cortante. La fuerza cortante es máxima en los
apoyos, pero la acción del campo de tensión no puede usarse en un tablero de
extremo. La separación de los atiesadores se determina como sigue:
•
Primera sección
a) Se iguala la resistencia requerida por cortante a la resistencia por cortante
dada por la ecuación 3.6.
Cv =
187.77
Vn
=
= 0.74
0.9( 0.6 Aw Fy ) (0.9 )(0.6 )(13 )(36 )
3.6
b) Se despeje K v de la ecuación 4.46.
2
Cv ⎛⎜ h ⎞⎟ FY
2
tw ⎠
(
0.74 )(208 ) (36 )
⎝
Kv =
=
= 26.30
44000
44000
4.46
c) Se calcula “a” de la ecuación 4.47.
a=h
5
Kv
5
= 25.19 in
4.47
Se usará una separación centro a centro del primer atiesador a = 25 in
113
Capitulo IV
Se Obtendrá la separación de los atiesadores intermedios ahora con la
resistencia requerida por cortante de Vn = 187.77 kips fuera de los tableros
extremos.
⎛ a ⎞
⎛ 25 ⎞
187.77 − w ⎜ ⎟ 187.77 − 5⎜ ⎟
⎝ 12 ⎠ =
⎝ 12 ⎠ = 196.73 kips
Vn =
0.9
0.9
4.48
Para los tableros extremos de trabes armadas no híbridas con acción de
campo de tensión tenemos que: a = 78 in 2
⎛
⎜ 5
Kv = 5 + ⎜
⎜a
⎝ h
( )
Cv =
2
44000Kv
=
2
⎛h ⎞ F
⎜ t ⎟ y
⎝ w⎠
4.12
⎞
⎟
⎟ = 7.22
⎟
⎠
44000 ⋅ 7.22
(52 0.25) 36
2
3.5
= 0.20
2
a
a ⎛⎜ 260 ⎞⎟
<
Como < 3 y
entonces hay campo de tensión.
h
h ⎜⎝ h tw ⎟⎠
Como
Kv
h
> 187
tw
Fy
⎡
⎤
⎢
⎥
1 - Cv
Vn = 0.6 Aw Fy ⎢Cv +
2 ⎥
⎢
⎥ (no satisfactorio)
1.15 1 + a
h ⎦
⎣
3.3
( )
= 165.10 kips < 196.73 kips
Se intentará con a = 52 in
Kv = 5 +
Cv =
5
(a h)
2
44000K v
2
4.12
= 10
⎛h ⎞ F
⎜ t ⎟ y
⎝ w⎠
=
44000 (10 )
(52 0.25) 36
2
= 0.283
3.5
114
Capitulo IV
2
a
a ⎛⎜ 260 ⎞⎟
entonces hay campo de tensión.
<
Como < 3 y
h
h ⎜⎝ h tw ⎟⎠
Como
Kv
h
> 187
tw
Fy
⎡
⎤
⎢
⎥
1 - Cv
Vn = 0.6 Aw Fy ⎢Cv +
2 ⎥
⎢
⎥ (satisfactorio)
1.15 1 + a
h
⎣
⎦
3.3
( )
= 203.21 kips > 196.73 kips
Se usará una separación centro a centro de atiesadores intermedios a = 52 in
•
Segunda sección
a = 300 in
⎛
⎜ 5
Kv = 5 + ⎜
⎜a
⎝ h
( )
Cv =
2
44000Kv
2
⎛h ⎞ F
⎜ t ⎟ y
⎝ w⎠
Como
4.12
⎞
⎟
⎟ = 5.15
⎟
⎠
=
(44000 )(5.15 )
(52 0.3125 ) 36
2
h
K
> 234 v
Fy
tw
3.5
= 0.146
Vn = Aw
4.75
26400kv
⎛h ⎞
⎜ t ⎟
⎝ w⎠
2
(no satisfactorio)
= 40.85 kips < 89.94 kips
Se intentará con a = 75 in
⎛
⎜ 5
Kv = 5 + ⎜
⎜a
⎝ h
( )
Cv =
2
44000K v
2
⎛h ⎞ F
⎜ t ⎟ y
⎝ w⎠
4.12
⎞
⎟
⎟ = 7.40
⎟
⎠
=
44000 ⋅ 7.40
(52 0.3125 ) 36
2
= 0.21
3.5
115
Capitulo IV
2
a
a ⎛⎜ 260 ⎞⎟
entonces hay campo de tensión.
<
Como < 3 y
h
h ⎜⎝ h tw ⎟⎠
Como
⎡
⎢
1 − Cv
Vn = 0.6 Aw Fy ⎢Cv +
2
⎢
1.15 1 + a
h
⎣
Kv
h
> 187
tw
Fy
( )
⎤
⎥
⎥
⎥ (satisfactorio)
⎦
3.3
= 168.75 kips > 89.94 kips
Se usará una separación centro a centro de atiesadores intermedios a = 75 in
•
Tercera sección
Vn
185.37
=
= 0.73
0.9( 0.6 A wFy ) (0.9 )(0.6 )(13 )(36 )
a)
Cv =
b)
Cv ⎛⎜ h ⎞⎟ FY
2
tw ⎠
(
0.73 )(208 ) (36 )
⎝
Kv =
=
= 25.96
44000
44000
c)
a=h
2
5
Kv
5
= 25.39 in
3.6
4.46
4.47
Se usará una separación centro a centro del primer atiesador a = 25 in
Se obtiene la separación de los atiesadores intermedios con la resistencia
requerida por cortante de Vn = 185.37 kips fuera de los tableros extremos.
Se introducimos el factor de reducción:
⎛ a ⎞
⎛ 25 ⎞
185.37 − w ⎜ ⎟ 187.77 − 5⎜ ⎟
⎝ 12 ⎠ =
⎝ 12 ⎠ = 194.06 kips
Vn =
0.9
0.9
4.48
116
Capitulo IV
Para los tableros extremos de trabes armadas no híbridas con acción de
campo de tensión se tiene que: a = 95 in
Kv = 5 +
Cv =
5
(a h)
2
44000Kv
2
⎛h ⎞ F
⎜ t ⎟ y
⎝ w⎠
Como
4.12
= 6.50
=
(44000 )(7.22) = 0.184
3.5
(52 0.25) 36
2
Kv
h
> 234
tw
Fy
⎤
⎡
⎢ 26400 k ⎥
v
⎥
Vn = Aw ⎢
2
(no satisfactorio)
⎢ ⎛h ⎞ ⎥
⎢ ⎜⎝ t w ⎟⎠ ⎥
⎦
⎣
= 51.54 kips < 194.06 kips
4.74
Se intentará con a = 48 in
Kv = 5 +
Cv =
5
(a h)
2
44000Kv
2
⎛h ⎞ F
⎜ t ⎟ y
⎝ w⎠
4.12
= 10.87
=
44000 ⋅ 10.87
(52 0.25) 36
2
3.5
= 0.307
2
a
a ⎛⎜ 260 ⎞⎟
Como < 3 y
entonces hay campo de tensión.
<
h
h ⎜⎝ h t w ⎟⎠
Como
h
K
> 187 v
Fy
tw
⎡
⎢
1 Cv
Vn = 0.6 Aw Fy ⎢Cv +
2
⎢
1.15 1 + a
h
⎣
= 210.55 kips > 194.06 kips
( )
⎤
⎥
⎥ (satisfactorio)
⎥
⎦
3.3
Se usará una separación centro a centro de atiesadores intermedios a = 48 in
117
Capitulo IV
Figura 4.40 Atiesadores.
Diseño de las dimensiones de los atiesadores intermedios
J=
2. 5
(a h)
2
−2=
2. 5
(a h)
2
3.20
− 2 = 8.82
3.19
I st = at w3 j = 52(0.25) 3 (8.82) = 7.16 in 4
Usando un valor máximo de
b
, se calcula “b” con la ecuación 4.49.
t
Después se despeja “t” de la ecuación 3.16.
b=
t=
bf − tw 14 − 0.35
=
= 6.88 in
2
2
b
95
= 0.43 in
4.49
4.50
Fy
Ast = 2b t = 2 6.88 0.43 = 5.97 in 2
4.51
Para 2 atiesadores:
⎡ 0.43(6.88 )2
2⎤
Ist 2 = ⎢
+ (0.43 )(6.88)(6.88 + tw 2) ⎥ × 2 = 245.34 in4
12
⎣
⎦
4.52
I st 2 > I st (satisfactorio)
118
Capitulo IV
Para determinar la longitud de los atiesadores, se calcula primero la
distancia entre la soldadura del atiesador y la soldadura del alma al patín. Las
Especificaciones del AISC indican una distancia mínima de 4t w y máxima de 6t w ,
por lo cual se utilizará una distancia de 5t w .
4.53
La = h - (5 t w - t w ) = 50.5 in
Se Usarán dos placas de
1
in × 6 in × 50.5 in para los atiesadores intermedios (ver
2
Figura 4.41.).
Figura 4.41 Atiesadores intermedios.
Los atiesadores de apoyo serán instalados en los soportes y debajo de
cada carga concentrada. Su diseño se realizará de la siguiente forma:
bf
14
−2 =
− 2 = 5 in
2
2
4.54
b Fy 5 36
=
= 0.316 in
t≥
95
95
4.55
b=
119
Capitulo IV
b = 5 in
Ensáyese una placa de atiesador de apoyo de
t=
5
in
16
Revísese la resistencia por aplastamiento.
φRn = 0.75( 1.8Fy Apb ) = 0.75( 1.8 )( 36 )( 0.316 )( 5 − 0.5 ) × 2
= 138.13 kips < 187.77 kips
(no satisfactorio)
4.22
b = 5 in
Debe aumentarse las dimensiones del atiesador.
φRn = 0.75(1.8Fy Apb ) = 0.75( 1.8 )( 36 )( 0.44 )( 5 − 0.5 ) × 2
= 192.8 kips > 187.77 kips
t=
7
in
16
4.22
(satisfactorio)
Revísese el atiesador como una columna.
4.23
A = 2bt + 12t w 2 = 5.16 in 2
I x = 70.05 in 4
r=
λc =
4.25
I
70.05
=
= 3.69 in
A
5.16
0.75h
πr Fy 29000
Como λc < 1.5
4.27
= 0.12
4.56
2
Fcr = 0.658 λc Fy = 35.79 ksi
φc Pn = φc Fcr A = 0.85(35.79)(5.16)
= 186.77 kips < 187.77 kips
4.29
(no satisfactorio)
Debe aumentarse las dimensiones del atiesador. b = 7 in y t =
9
in
16
120
Capitulo IV
A = 2bt + 12t w 2 = 2(0.57)(5) + 12(0.25) = 6.41 in 2
4.23
I x = 89.89 in 4
r=
λc =
4.25
I
89.89
=
= 3.75 in
A
6.41
0.75h
πr Fy 29000
Como λc < 1.5
4.27
= 0.12
Fcr = 0.658 λ2c Fy = 35.8 ksi
φc Pn = φ c Fcr A = 0.85(35.8)(6.41) = 194.97 kips > 187.77 kips (satisfactorio)
Empléense dos placas de 5 in ×
4.56
4.29
9
in en los atiesadores de apoyo (Figura 4.42.).
16
Figura 4.42 Atiesador de apoyo.
Se han dimensionado todas las componentes de la trabe armada. Las
conexiones de esos elementos serán diseñadas. Se utilizarán electrodos E60 con
una resistencia de diseño de φFw = 27 ksi .
121
Capitulo IV
a) Calcúlese la separación de la soldadura entre el alma y el patín.
G=
4.57
peralte t f
− = 26.75 in
2
2
4.58
Q = área del patín × G = 14(1.5) × 26.75 = 561.75 in 3
I xx
4.59
tw h 3
=
+ 2(bf t f G 2 ) = 32982 .96 in 4
12
Maximo =
4.60
187.77(561.75 )
kips
= 3 .2
32982,96
in
Para los espesores de placa por soldar se usará un tamaño de soldadura
de w = t w . La longitud mínima de soldadura se calcula con la ecuación 4.61.
Lmin = 4(w ) ≥ 1.5 in
4.61
Lmin = 4(0.25 ) = 1 in Usaremos 1.5 in.
Ensáyese soldaduras de filete de
1
in × 1.5 in ,
4
La capacidad por pulgada de 2 soldaduras se muestra en la ecuación 4.62.
Capacidad por pulgada = 2(0.707w φFw )
4.62
= 2(0.707 )(0.25 )(27 ) = 9.54
kips
in
La capacidad por cortante del metal base se calcula con la ecuación 4.63.
t (φFBM ) = tw [(.9(0.60Fy ))] = 0.25(0.54)(36 ) = 4.86
kips
in
4.63
La capacidad de un par de soldaduras de 1.5 in se calcula con la ecuación
4.64.
[
]
Lsoldadura t w (0.9(0.60Fy )) = 4.86(1.5) = 7.29 kips
4.64
122
Capitulo IV
Para determinar la separación de las soldaduras se calculará “s”.
s=
7.29 7.29
=
= 2.28 in < 12 in (satisfactorio)
VuQI x 3.20
4.65
Aunque la separación s = 2.28 in centro a centro se utiliza para toda la
longitud de la trabe, una mayor separación puede usarse donde la fuerza cortante
es menor que la máxima de 187 kips. Se investigará una separación de 5
pulgadas, ver ecucacion 4.66.
Vu 2 =
7.29(32982 )
= 85.7 kips
561(5 in)
4.66
Refiérase a la Figura 4.38 y sea “x” la distancia desde el soporte izquierdo,
ver ecuación 4.67.
x=
187 − 85.7
= 19.8 ft
5 .1
4.67
Figura 4.43 Soldadura Alma-Patín.
123
Capitulo IV
b) Calcúlese la separación de los atiesadores intermedios.
Tamaño mínimo de soldadura =
3
in
16
⎡3⎤
Longuitud mínima = 4 ⎢ ⎥ = 0.75 in < 1.5 in Usaremos 1.5 in.
⎣16 ⎦
f = 0.045h
Fy3
(36 )3
kips
= 0.045(52)
= 2.97
E
29000
in
4.68
4.69
3.21
La separación máxima permisible de la soldadura es:
4.70
16t w = 16(0.25 ) = 4 in
s=
7.29
= 2.46 in < 4 in (satisfactorio)
2.97
Usaremos soldadura de filete de
4.71
1
in × 1.5 in para los atiesadores intermedios.
4
c) Calcúlese la soldadura de los atiesadores de apoyo:
Longuitud mínima = 4t w = 4(0.25 ) = 1 in < 1.5 in Usaremos 1.5 in.
4.69
Tamaño mínimo = t w = 0.25 in
4.68
Re acción
187.77
kips
=
= 3.72
Longuitud disponible para soldadura 52 - 1.5
in
4.72
s=
4.73
7.29
= 1.96 in
3.72
Se usará soldadura de filete de
1
in × 1.5 in para los atiesadores de apoyo.
4
124