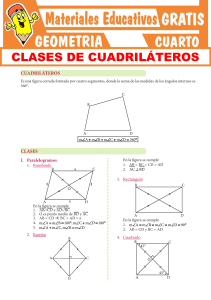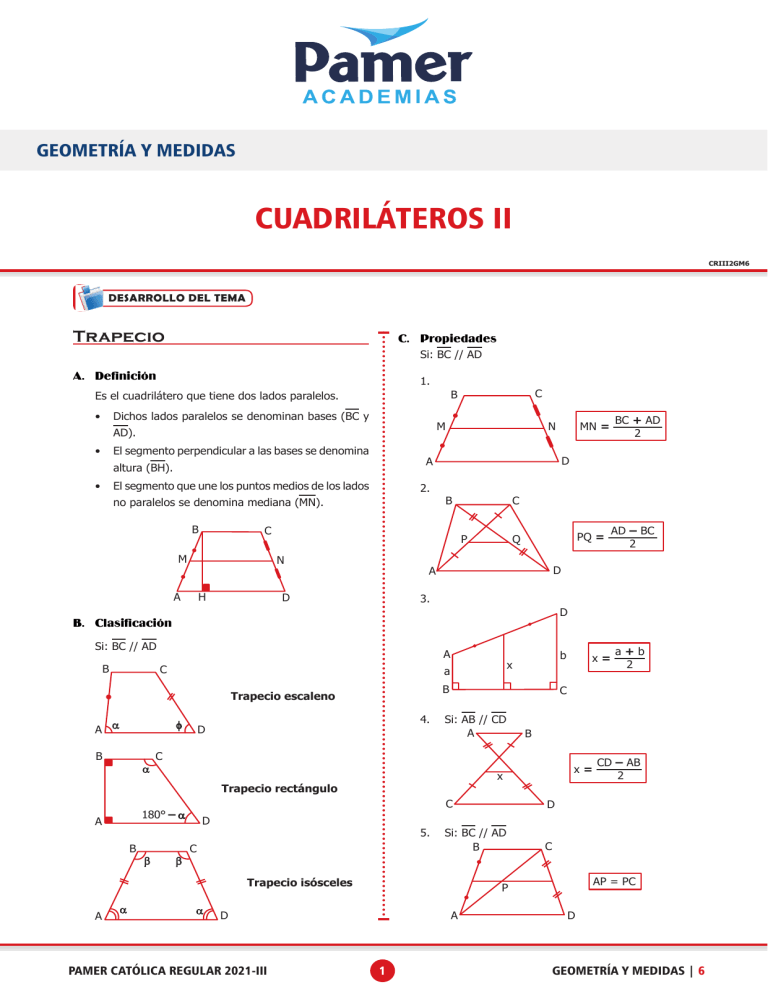
GEOMETRÍA Y MEDIDAS CUADRILÁTEROS II CRIII2GM6 DESARROLLO DEL TEMA Trapecio C. Propiedades Si: BC // AD A. Definición 1. Es el cuadrilátero que tiene dos lados paralelos. • Dichos lados paralelos se denominan bases (BC y M AD). • El segmento perpendicular a las bases se denomina El segmento que une los puntos medios de los lados 2. no paralelos se denomina mediana (MN). B H A C B PQ = Q P N 3. D B. Clasificación Si: BC // AD B A C A a φ B a B 4. D 180° – a B b Si: AB // CD A b 5. C a a D Si: BC // AD B C A 1 CD – AB 2 AP = PC P D PAMER CATÓLICA REGULAR 2021-III x= C Trapecio isósceles A a+b 2 B x D x= C C Trapecio rectángulo A b x a Trapecio escaleno AD – BC 2 D A D BC + AD 2 D C M MN = N A altura (BH). • C B D GEOMETRÍA Y MEDIDAS | 6 CUADRILÁTEROS II 6. En un trapecio isósceles B f a a 2. f y w C x + y + w + z = 360° x b a b a A z 3. D a B A b a+b=x+y x y C a a x b a 7. En un trapecio isósceles D m x= b–a 2 m= a+b 2 4. a a+b=x+y x y b 5. B Trapezoide a a b x C b x= A+D 2 A. Definición Es el cuadrilátero convexo que no tiene lados paralelos. 6. C B AB no es // CD BC no es // AD A D A B a a C x D b A x= C–A 2 b (C > A) D Observación: B. Trapezoide simétrico • Denominado también trapezoide bisósceles, es cuando una diagonal es mediatriz de la otra diagonal. B A a q • B C ff C. Propiedades que se cumplen en todo cuadrilátero • 1. B q E D Se traza una paralela a un lado D E Se forma un paralelogramo A b Se traza una paralela a un lado Se forma un paralelogramo b b a q C C Se forman triángulos congruentes a + b + q + f = 360 a f PAMER CATÓLICA REGULAR 2021-III A 2 D GEOMETRÍA Y MEDIDAS | 6 CUADRILÁTEROS II PROBLEMAS RESUELTOS Problema 1 Si ABCD es un rombo, AH = 3 y HD = 2. Calcula BH. B C A A. 4 B. 3 Problema 2 En un romboide ABCD; AB = 4 y BC = 10. Luego se trazan las bisectrices interiores de B y C que cortan a AD en E y F respectivamente. Calcula EF. A. 5 C. 2 B. 6 D. 8 D H C. 5 D. 2 Resolución B 5 Por lo tanto BH = 4. Respuesta: A. 4 Resolución B 5 C 4 4 5 10 a a a b 4 4 E F Lados AB = CD = 4 Lados BC = AD = 10 A A D 2 3 H En el rombo todos los lados son iguales: AB = BC = CD = DA = 5 Entonces: AHB rectángulo y aproximado. b b 4 C Por lo tanto: ∆ ABE isósceles: AB = AE = 4. ∆ CDF isósceles: CD = FD = 4. y EF = 2 Respuesta: C. 2 Problema 3 Los ángulos internos de un trapezoide estan en la relación 2, 3, 4 y 6. Calcula el menor ángulo del trapecio. A. 56° C. 48° B. 52° D. 44° Resolución 4k 3k D 6k 2k Suma de ángulos interiores: 2k + 3k + 4k + 6k = 360° 15k = 360° k = 24° Entonces: 2k = 2(24) = 48° Si BC//AD entonces: m∠CBE = m∠BEA Alternos m∠BCF = m∠CFD Internos Respuesta: C. 48° EJERCICIOS DE CLASE Nivel I 3. De la figura, halla MN, si M y N son puntos medios de AD y BC, respectivamente. 1. Calcular el perímetro del cuadrilátero ABCD mostrado en la figura. B 20 cm 120° 40 cm C A 30° A C. (90 + 30 3) cm D. (80 + 20 3) cm 2. En la figura mostrada, calcula BC, si ABCD es un trapecio isósceles. B C 120° A. 10 m M N 8 cm B D D A. (70 + 30 3) cm B. (90 + 10 3) cm A 6 cm C B. 6 m GEOMETRÍA Y MEDIDAS | 6 C. 3 cm B. 2 cm D. 1,5 cm 4. En un trapecio isósceles, las diagonales miden 16 cm 8m 20 m C. 8 m A. 1 cm y son perpendiculares a sus lados oblicuos si la base mayor mide 20 cm halla la longitud de la base menor. D D. 12 m 3 A. 5,6 cm C. 6,8 cm B. 7,2 cm D. 7 cm PAMER CATÓLICA REGULAR 2021-III CUADRILÁTEROS II 5. En el trapecio ABCD, AM = MB y BC = CN = ND. Halla x. B C B. x a M A. a A N A. 1 C. 2 B. 1,5 D. 3 B. C. 5 m 13 m D. 10 m D. b 2 12. En un trapecio isósceles la altura es congruente con la mediana. Calcular el ángulo que forman las diagonales del trapecio al intersectarse. A. 53° C. 45° B. 90° D. 60° Nivel II 7. En la figura mostrada BC = 5 y AD = 9 2. Si CM = MD, calcular MH. 13. En el trapecio ABCD; BC//AD, CM//AB y BN//CD. Halle AB + CD si BP = (x – 12) m, PC = 6 m, PM = (x + 8) m y PN = 16 m. B 37° B H C C P M 45° A D A. 6 C. 7 B. 6,5 D. 8 A q N D C. 50 m D. 44 m 14. En la figura adjunta: BC = 6; CD = 3 3 . Calcular AB B C 120 150 C 30 P q A A. 10 cm B. 11 cm C. 13 cm D. 12 cm A. 15 B. 12 D P O PAMER CATÓLICA REGULAR 2021-III C. 9 D. 18 D 16. Dos alumnos de la universidad desean medir la altura del edificio Dintilhac, para lo cual cuentan con un báculo de 4 m de altura. Uno de los alumnos se coloca como muestra la figura. ¿Cuál es la altura de dicho edifico? N A A 15. En un trapezoide ABCD, halle el menor ángulo formado por las bisectrices interiores de B y D, si ∠C – ∠A = 66°. A. 43° C. 28° B. 33° D. 30° 9. Si M es punto medio de AB y N es punto medio de CD si AD = a y BC = b, halle MP + QN. B C M M A. 80 m B. 75 m 8. En el gráfico se tiene el trapecio ABCD y AP = BP. Si PQ = 9 cm y BC = 6 cm calcule: AD. Q B 2 11. En un trapecio isósceles, la suma de las longitudes de las bases es 24 cm y la altura mide 5 cm. Halle la suma de las longitudes de las diagonales. A. 26 cm C. 18 cm B. 24 cm D. 28 cm 6. Se tiene un cuadrilátero ABCD en el cual AB = BC = 8 m, ∠ABC = 60°, ∠DAC = 90° y AD = 6 m. Calcula la longitud del lado DC. A. 8 m a+b a–b 10. En un trapecio los ángulos adyacentes a la base menor miden 110° y 140°. La diferencia de las medidas de las bases es 17 metros. Calcular la longitud del mayor de los lados no paralelos. A. 8,5 m C. 12,5 B. 11 m D. 17 m D 2a + 3 C. D 4 GEOMETRÍA Y MEDIDAS | 6 CUADRILÁTEROS II A. 1 m B. 1,2 m 1,70 m 4m alumno báculo 10 m A. 11,5 m B. 13,2 m 19. En la figura, ABCD es un paralelogramo donde AB = 33 cm y 11(EQ) = 3(BE). Calcule MN si M es el punto medio de BQ y N es el punto medio de AP. edificio 50 m B C C. 13,8 m D. 15,5 m P E Nivel III A 17. En un cuadrilátero ABCD, A = C = 90. Si "O" es el punto medio de la diagonal BD y B = 124°, calcular la medida del ángulo AOC. A. 84° C. 124° B. 112° D. 108° A. 8 cm B. 9 cm D Q C. 11 cm D. 12 cm 20. Los lados oblicuos de un trapecio son 4 y 6. Calcular el máximo valor entero que toma el segmento que une los puntos medios de las diagonales. A. 3 C. 5 B. 4 D. 6 18. En un trapecio ABCD, BC//AD, BC = 4 m, AD = 6 m y la altura mide 8 m. Halle la distancia del punto de corte de las diagonales a la mediana del trapecio. GEOMETRÍA Y MEDIDAS | 6 C. 0,8 m D. 0,6 m 5 PAMER CATÓLICA REGULAR 2021-III