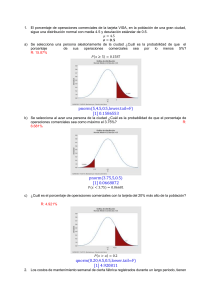
DISTRIBUCIONES CONTINUAS EN INFERENCIA ESTADÍSTICA Distribución Normal. Normal Estándar. Propiedades: 1. Los gastos de viajes semanales que el personal de ventas de una empresa reporta tienen una distribución Normal con media igual a 950.25 soles y desviación estándar igual a 30.35 soles. a) Determine el porcentaje de los vendedores que reportan gastos superiores a 1000 soles. R: 5.0585% #Pregunta 1 #a) P(x>1000) pnorm(1000,950.25,30.35,lower.tail = F) b) Determine cuántos de los 50 vendedores que tiene la empresa reportaran gastos superiores a S/ 1000 R:3 vendedores =0.05058*50=2.529≈3 round(50*pnorm(1000,950.25,30.35,lower.tail = F)) c) El gerente ha ofrecido vacaciones de dos semanas a quien justifique gastos que se encuentren en el 15% inferior. Si Juan Pérez. ha gastado 712 soles, conseguirá las vacaciones? Justifique su respuesta. R: K= 918.794. Juan Pérez si debe conseguir las vacaciones. qnorm(0.15,950.25,30.35) [1] 918.7942 Si conseguirá las vagaciones. 2. Las horas productivas (horas que se han trabajado) por mes en un departamento de administración tienen distribución Normal con media igual a 1500. Se sabe que en el 15% de los meses las horas productivas son más de 1600. a) ¿Cuál es el valor de la desviación estándar? R: 96.525 𝜇 = 1500 𝑃(𝑥 > 1600) = 0.15 𝑥 − 1500 1600 − 1500 𝑃( > ) = 0.15 𝜎 𝜎 100 100 𝑃 (𝑍 > ) = 0.15 → 𝑍 > 1.036 → 1.036 = → 𝝈 = 𝟗𝟔. 𝟓𝟐𝟓𝟏 𝜎 𝜎 b) ¿Cuál es la probabilidad de que en un mes se trabajen entre 1450 y 1550 horas? 0.3957 𝑃(1450 < 𝑥 < 1550) = R: pnorm(1550,1500,96.5251)-pnorm(1450,1500,96.5251) [1] 0.3955417 c) Si se seleccionan 5 meses al azar, ¿cuál es la probabilidad de que en 3 de ellos se hayan trabajado entre 1450 y 1550 horas? R: 0.2263 Binomial: 𝑃(1450 < 𝑥 < 1550) = 0.3955417 𝐵~(𝑛, 𝑝) 𝐵~(5,0.3955417) 𝑃(𝑥 = 3) = 0.2261 dbinom(3,5,0.3955417) [1] 0.2261047 3. El porcentaje de operaciones comerciales de la tarjeta VISA, en la población de una gran ciudad, sigue una distribución normal con media 4.5 y desviación estándar de 0.5. 𝜇 = 4.5 𝝈 = 𝟎. 𝟓 a) Se selecciona una persona aleatoriamente de la ciudad ¿Cuál es la probabilidad de que el porcentaje de sus operaciones comerciales sea por lo menos 5%? R: 15.87% 𝑃(𝑥 ≥ 5) = 0.1587 pnorm(5,4.5,0.5,lower.tail=F) [1] 0.1586553 b) Se selecciona al azar una persona de la ciudad ¿Cuál es la probabilidad de que el porcentaje de operaciones comerciales sea como máximo el 3.75%? R: 6.681% pnorm(3.75,5,0.5) [1] 0.0668072 𝑃(𝑥 < 3.75) = 0.06681 c) ¿Cuál es el porcentaje de operaciones comerciales con la tarjeta del 20% más alto de la población? R: 4.921% 𝑃(𝑥 > 𝑎) = 0.2 qnorm(0.20,4.5,0.5,lower.tail=F) [1] 4.920811 4. Los costos de mantenimiento semanal de cierta fábrica registrados durante un largo periodo, tienen una distribución Normal con una media igual a 1,680 soles; además se sabe que 0.70 es la probabilidad de que el costo de una semana sea como máximo 1,627.56 soles. 𝜇 = 1680 𝑥 − 1680 1627.56 − 1680 𝑃( ≤ ) = 0.7 𝜎 𝜎 1627.56 − 1680 𝑃 (𝑍 ≤ ) = 0.7 𝜎 qnorm(0.7) [1] 0.5244005 𝑍= 1627.56 − 1680 1627.56 − 1680 = 0.5244005 → σ = = −100 𝜎 0.5244005 𝝈 = 𝟏𝟎𝟎 a) Hallar el valor de la desviación estándar de la distribución Normal. R: 100 b) Hallar la probabilidad de que el costo de una semana se diferencie del promedio en no más de 150 soles. R: 0.8663858 𝑃(1680 − 150 < 𝑥 < 1680 + 150) = 𝑃(1530 < 𝑥 < 1830) pnorm(1830,1680,100)-pnorm(1530,1680,100) [1] 0.8663856 c) ¿Cuál será el costo semanal máximo que se observará en una semana con probabilidad 0.75? R: 1747.45 qnorm(0.75,1680,100) [1] 1747.449