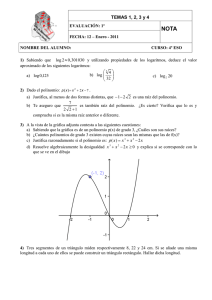
. En el aula virtual se les presenta el siguiente problema, de cómo construirían una caja de cartón rectangular de 80 cm de largo y 60 cm de ancho. Se confecciona el polinomio que expresa el volumen de la caja. Considera como variable la altura x. x a. LA ACCIÓN REAL EJERCIDA POR LA O EL ESTUDIANTE • Realiza un esquema con las dimensiones del cartón, donde se recortarán de cada esquina un cuadrado. • Ahora realiza un bosquejo con todas las dimensiones • Desarrollar el volumen de la caja de cartón b. LA ACCIÓN ACOMPAÑADA POR EL LENGUAJE 60 ¿Qué características de la caja de cartón? Los lados opuestos tienen las mismas medidas 80 80 60 ¿Crees que el tamaño del cuadrado que se recorta haga que cambie el volumen de la caja? Si produce cambios en el volumen de la caja, si varían sus medidas en cada x provocara que no se logre construir la caja ¿hay algo que pueda afirmar que la caja puede aumentar de volumen? La caja de cartón aumentara de volumen de acuerdo a lo siguiente ¿V? V= 4𝑿𝟑 -280𝑿𝟐 +4800𝑿𝟏 c. LA CONDUCTA DEL RELATO V= polinomio Encuentra una expresión algebraica que permita conocer el volumen de la caja a partir de su altura ¿Es posible hallar el volumen de una caja conociendo con solo 2 dimensión? ¿V y h? ¿El volumen de la caja aumenta y disminuye al incrementar la altura de la caja? ¿V? d. REPRESENTACIÓN GRÁFICA Deducimos la expresión matemática. =(80-2x)(60-2x)(x) =2*2(x)(40-x)(30-x) =4(x)(40-x)(30-x) =4(x)(1200-70x+ 𝑥 2 ) =4(x)(𝑥 2 -70x+1200 ) =(4𝑥 3 -280𝑥 2 +4800x) Representamos mediante símbolos matemáticos. 𝒇(𝒙) = (𝟒𝒙𝟑 − 𝟐𝟖𝟎𝒙𝟐 + 𝟒𝟖𝟎𝟎𝒙) Calculamos el volumen proponiendo valores a x (altura) Altura de la caja x 1 2 3 4 5 6 7 8 9 Volumen de la caja f(x) 4524 8512 11988 14976 17500 19584 21252 22528 23436 • SI quisiéramos hacer una caja con una altura de 9 cm • • ¿Cuál sería el volumen de dicha caja? Explica que ocurre con el volumen cuando hacemos una caja con una altura de 20 cm