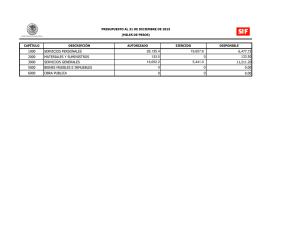
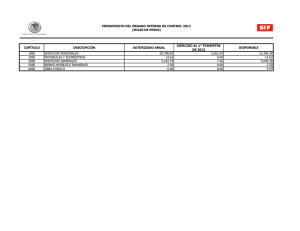
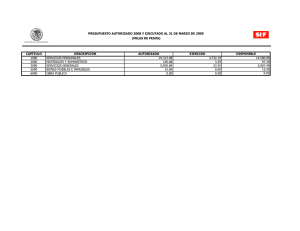
SEPI - UPIICSA – IPN Investigación de operaciones Avanzada Maestría en Ingeniería Industrial Sesión 7 Programación por metas Introducción Se ha visto que un modelo de programación lineal está constituido de una o más restricciones, pero de una sola función objetivo. Sin embargo, en muchas de sus aplicaciones pueden existir objetivos múltiples. En estos casos no se deben aplicar los modelos lineales de la forma que hemos revisado. Además en muchas ocasiones no se obtiene la solución óptima, sino la más factible. Lo anterior se debe a que los objetivos múltiples pueden ser opuestos y por consiguiente sería sumamente difícil que una solución que resulta óptima en la minimización de recursos sea la misma para el caso de maximización de recursos. Por tales razones sólo se habla de soluciones eficientes. Se puede decir que la programación por metas es una técnica de la investigación de operaciones y una herramienta de toma de decisiones dentro de la organización. La programación por metas sirve para tratar problemas de decisión gerencial que comprenden metas múltiples de acuerdo a la importancia que se les asigne a éstas. El generador de decisiones (directivo) debe ser capaz de establecer al menos una importancia, para clasificar dichas metas. Programar por metas es realizar un modelo de programación lineal donde se tenga una función objetivo que optimizar y sujeta a una o varias restricciones. Sin embargo, se caracteriza por dos conceptos nuevos. El primero es el de las restricciones de meta en lugar de las restricciones de recurso o disponibilidad y el segundo concepto es el de rango de prioridad entre las funciones de objetivo. Ventajas de la programación por metas: • Una ventaja de la programación por metas es su flexibilidad en el sentido de que permite al directivo que toma las decisiones, experimentar con una multitud de variaciones de las restricciones y de prioridades de las metas cuando se involucra con un problema de decisión de objetivos múltiples. • Permite tomar decisiones más estudiadas, no decisiones arbitrarias que lo único que pueden ocasionar es la inestabilidad económica de la empresa. PASOS EN LA FORMULACIÓN DE UN MODELO DE PROGRAMACIÓN POR METAS: • Fijar los atributos que se consideran relevantes para el problema que se está analizando. Este concepto se refiere a valores de la gerencia relacionados con una realidad que se pueda alcanzar. Estos valores pueden medirse independientemente de los deseos del centro decisor, siendo usualmente susceptibles de expresarse como una función matemática de las variables de decisión. 1 Elaboró Dr. Eduardo Gutiérrez González • Determinar el nivel de aspiración (meta) que corresponde a cada atributo, es decir, el nivel de logro que la gerencia desea alcanzar. Definir si se quiere maximizar o minimizar el atributo. • Conectar el atributo con el nivel de aspiración, por medio de la introducción de las variables de déficit y exceso. Las variables de déficit cuantifican la falta de logro de una meta con respecto a su nivel de aspiración, mientras que las variables de exceso cuantifican lo que sobrepaso el logro de una meta con respecto a su nivel de aspiración. • Establecer el concepto de variable de decisión no deseada. Una variable de decisión se dice que no es deseada cuando al gerente de la empresa le interesa que la variable en cuestión alcance su valor más pequeño (esto es cero). Cuando la meta u objetivo es maximizar, la variable no deseada es minimizar. Finalmente, cuando se desea alcanzar exactamente el nivel de aspiración tanto la variable de déficit como la de exceso son variables no deseadas y por tanto variables a minimizar. FUNCIÓN OBJETIVO La función objetivo para un problema de programación por meta siempre es minimizar alguna combinación de variables de déficit. Desde un punto de vista de toma de decisiones administrativa, esto significa que se está buscando la combinación de variables reales por ejemplo (mesas y sillas) que cumplan mejor con todos los objetivos. Esto podría llamarse optimizar un conjunto de objetivos "satisfactorios" o a satisfacer. La forma exacta de la función objetivo varia según la respuesta a estas dos preguntas: 1. ¿Son conmensurables o proporcionales los objetivos? 2. ¿Cuál es la importancia relativa de cada objetivo? • Objetivos conmensurables de igual importancia: este es el caso más sencillo, aunque muy pocas veces se encuentra en la práctica. Aquí los objetivos se miden en una escala común y tienen la misma importancia. • Ponderación preferente de los objetivos: las ponderaciones de preferencia pueden aplicarse a cualquier grupo de objetivos conmensurables. Las ponderaciones deben reflejar la utilidad o el valor de los objetivos. • Rango de prioridad de los objetivos: ¿qué pasa cuando los objetivos no son conmensurables, cuando no hay una escala común para comparar las desviaciones de los diferentes objetivos?. Este es un caso importante, al que se enfrentan con frecuencia los administradores. Si el administrador puede ordenar o dar un rango para sus metas entonces la solución es posible. Quizás no sea una tarea fácil dar un rango a los objetivos de acuerdo con su importancia pero es algo que la mayoría de las personas entienden y pueden lograr. En la programación por objetivos se le asigna la prioridad P1 al objetivo más importante, siguiendo P2 a una prioridad más baja. No existe límite en el número de niveles de prioridad pero debe asignarse una prioridad para cada variable de déficit o exceso. Se permiten empates o prioridades iguales. Los problemas de programación por meta se resuelven en orden de prioridad. Es decir, se prueba la optimización en el nivel de prioridad más alto ignorando las prioridades más bajas hasta optimizar este nivel. 2 Investigación de Operaciones Avanzada. Sesión 7 En esta sesión revisaremos los métodos más comunes de soluciones eficientes, cuando tenemos un problema con objetivos múltiples. 1.- MÉTODO DE UN SÓLO OBJETIVO Este método se utiliza cuando dos o más objetivos están en conflicto y consiste en proponer un objetivo como la función objetivo y los demás objetivos plantearlos como restricciones. EJEMPLO 1 Considere la problemática de un administrador forestal. La ley especifica que debe administrar el bosque de manera de estimular el crecimiento de árboles, aumentando los refugios para los animales y que lo haga a costo mínimo. Suponga que existen dos actividades básicas: limpiar el bosque (cortar arbustos) y abrir brechas contra incendio. Cada una de estas actividades tiene un costo y requiere mano de obra. También produce beneficios y daños. En la tabla de abajo se muestran los parámetros asociados a una hectárea de bosque limpiada y un kilómetro de brecha para incendio. Actividad forestal Concepto Limpieza Abrir brecha Costo um 500 500 Costos Mano de obra (horas) 150 50 Crecimiento árboles −5 10 Beneficios 60 Refugio para animales − 10 Los recursos que dispone el administrador son: 90,000 horas de trabajo, las condiciones del bosque limitan los kilómetros de brecha contra incendio a 300 y el presupuesto disponible es de 350,000um. El problema del administrador consiste en determinar el número de hectáreas limpias ( x1 ) y los kilómetros de brecha abiertos ( x 2 ), para que proporcione el máximo crecimiento de los árboles y todo el refugio posible para los animales. Solución Vemos que tenemos dos objetivos Crecimiento de árboles: max Z = 10 x1 − 5 x 2 Refugio de animales: max Z = −10 x1 + 60 x 2 Las restricciones son: 150 x1 + 50 x 2 ≤ 90000 x 2 ≤ 300 500 x1 + 500 x 2 ≤ 350000 Para resolver el problema buscamos la frontera eficiente, la misma que obtenemos al proponer una de las funciones objetivo como restricción. En este caso tenemos dos objetivos el crecimiento de árboles y la cantidad de refugios, para ejemplificar proponemos a los refugios como una nueva restricción, pero para esto requerimos una acotación de los refugios en este caso debe ser una cantidad mínima que se quiera satisfacer. Vamos a determinar la frontera eficiente, dando valores mínimos a los refugios, desde cero hasta 16,500 con saltos de 500 refugios. Es decir, el problema a resolver será: 3 Elaboró Dr. Eduardo Gutiérrez González max Z = 10 x1 − 5 x 2 150 x1 + 50 x 2 x2 500 x1 + 500 x 2 − 10 x1 + 60 x 2 ≤ 90000 ≤ 300 ≤ 350000 ≥c En donde, c representa los requerimientos mínimos de refugio a satisfacer y le daremos los valores de: 500, 1000, 1500, 2000, etc. sus resultados se muestran en la siguiente tabla. Refugio Árboles X1 X2 Refugio Árboles X1 X2 0 500 1000 1500 2000 2500 3000 3500 4000 4500 5000 5500 6000 6500 7000 7500 8000 5211 5145 5079 5013 4947 4882 4816 4750 4643 4536 4429 4321 4214 4107 4000 3893 3786 568 566 563 561 558 555 553 550 543 536 529 521 514 507 500 493 486 95 103 111 118 126 134 142 150 157 164 171 179 186 193 200 207 214 8500 9000 9500 10000 10500 11000 11500 12000 12500 13000 13500 14000 14500 15000 15500 16000 16500 3679 3571 3464 3357 3250 3143 3036 2929 2821 2714 2607 2500 2000 1500 1000 500 0 479 471 464 457 450 443 436 429 421 414 407 400 350 300 250 200 150 221 229 236 243 250 257 264 271 279 286 293 300 300 300 300 300 300 16000 15000 14000 13000 12000 11000 10000 9000 8000 7000 6000 5000 4000 3000 2000 1000 Curva de la frontera eficiente para el objetivo de árboles 5500 5000 4500 4000 3500 3000 2500 2000 1500 1000 500 0 0 Cantidad de Árboles Gráficamente la frontera eficiente se muestra a continuación. Cantidad de refugios Ahora la elección de cuántos refugios pedir se debe cumplir y con ello tendremos la maximización de los árboles. 4 Investigación de Operaciones Avanzada. Sesión 7 2.- MÉTODO PONDERACIÓN DE OBJETIVOS Este método se utiliza cuando se tienen dos o más objetivos que son del mismo tipo, ya sea maximizar o minimizar. El método consiste en ponderar los objetivos y sumarlos. EJEMPLO 2 En el ejemplo anterior tenemos dos objetivos similares de maximización, por tales razones si es posible ponderar las unidades de árboles y las de refugio, podemos establecer un problema de ponderación de objetivos. Solución En este caso se puede apreciar que una ponderación factible se puede hacer con el dinero. Supóngase que una unidad de crecimiento de árbol es equivalente a 600um y una unidad de refugio para animales es equivalente a 100um. De la tabla anterior tenemos dos actividades forestales y cada una de ellas la vamos a ponderar. Limpieza: Por cada hectárea que se limpie se producen 10 unidades de árboles y se eliminan 10 unidades de refugio para animales con un costo de 500um. 10(600) − 10(100) − 500 = 4500 um. Abrir brecha: Por cada kilómetro abierto de brecha contra incendio se producen 60 unidades de refugio y se eliminan 5 árboles con un costo de 500um, de donde el beneficio neto − 5(600) + 60(100) − 500 = 2500 um. Por lo tanto, el problema a resolver estará dado por: max Z = 4500 x1 + 2500 x 2 Las restricciones son: 150 x1 + 50 x 2 ≤ 90000 x 2 ≤ 300 500 x1 + 500 x 2 ≤ 350000 Ejemplo 2 Horas de trab. Km de brecha Presupuesto Max árboles Solución X1 150 500 4500 550 X2 50 1 500 2500 150 90000 150 350000 2850000 <= <= <= 90000 300 350000 Luego, cuando se limpian 550 hectáreas y abriendo 150 kilómetros de brecha se tiene la utilidad máxima de 2,850,000um. 3.- MÉTODO PROGRAMACIÓN CON METAS Este método se utiliza cuando el decisor especifica las metas deseables en cada objetivo. Para que sea factible alcanzar una meta se tiene que introducir dos tipos de variables en cada objetivo, una para que tome valores en caso de no alcanzar la meta (déficit, Di ) y la otra para que tome valores en caso de pasar la meta (exceso, E i ). Así, al problema original se le agregan las restricciones de 5 Elaboró Dr. Eduardo Gutiérrez González cada objetivo, mientras que la función objetivo estará formada por la minimización de los déficit y excesos que se agregaron a cada objetivo si es que son ponderados con algún costo. EJEMPLO 3 En el ejemplo 1 suponga que el decisor especifica metas deseables para cada uno de los dos objetivos, que consisten en 5000 unidades de árboles y 6000 unidades de refugio. Además de tener como meta el no sobrepasar el presupuesto, en caso de sobrepasarlo se penaliza cada unidad que sobrepase con 5um. Solución En este caso denotamos los déficits por Di y los excesos por E i , de tal forma que las restricciones son: 150 x1 + 50 x 2 x2 500 x1 + 500 x 2 + D3 − E3 10 x1 − 5 x 2 + D1 − E1 − 10 x1 + 60 x 2 + D2 − E 2 ≤ 90000 ≤ 300 = 350000 = 5000 = 6000 Para poder establecer una función objetivo requerimos ponderar las variables de déficit y las de exceso para que estén en las mismas unidades y se puedan comparar. Así, la carencia de una unidad de árbol vale 600um y la de refugio 100um, mientras que si los excesos se penalizan (no siempre ocurre), por ejemplo un exceso en una unidad de árbol es 50um y la de refugio de 25um, tendremos: min Z = 600 D1 + 100 D2 − D3 − 50 E1 − 25 E2 + 5 E3 Sujeta a 150 x1 + 50 x 2 x2 500 x1 + 500 x 2 + D3 − E3 10 x1 − 5 x 2 + D1 − E1 − 10 x1 + 60 x 2 + D2 − E 2 Horas de trabajo. Km de brecha Presupuesto X1 X2 150 50 500 10 -10 1 500 -5 60 MIN-DEFICIT Solución 550 150 D1 D2 D3 E1 E2 1 1 1 600 100 250 2500 ≤ 90000 ≤ 300 = 350000 = 5000 = 6000 E3 -1 -1 -1 0 -50 0 -1 -25 0 5 0 90000 <= 90000 150 350000 5000 6000 $400,000 <= = = = 300 350000 5000 6000 6 Investigación de Operaciones Avanzada. Sesión 7 En estas condiciones sobre la optimización de metas, obtenemos la solución más eficiente cuando se limpian 550 hectáreas y se abre brecha en 150 kilómetros. Con los siguientes déficit en árboles y unidades de refugio de 250 y 2,500, respectivamente (sus metas eran 5000 y 6000). 4.- MÉTODO PROGRAMACIÓN CON PRIORIDADES Este método es casi idéntico al anterior, pero en lugar de una sola función objetivo con todas las variables de déficit y exceso, se va resolviendo un problema simplex para cada variable, según sea su prioridad establecida por el decisor. El proceso de pruebas termina cuando una de estas variables toma valores diferentes de cero y las demás prioridades no se consideran. EJEMPLO 4 En el ejemplo anterior suponga las siguientes prioridades: 1. Minimizar el déficit de árboles, D1 . 2. Minimizar el déficit de refugio, D2 . 3. Minimizar el exceso de presupuesto, E 3 . 4. Maximizar el exceso de refugio, E 2 . 5. Maximizar el exceso en árboles, E1 . 6. Maximizar el déficit de presupuesto, D3 . Solución min Z = D1 min Z = D2 Sujeta a Sujeto a 150 x1 + 50 x 2 x2 500 x1 + 500 x 2 + D3 − E3 10 x1 − 5 x 2 + D1 − E1 − 10 x1 + 60 x 2 + D2 − E 2 D1 Horas de trab. Km de brecha Presupuesto X1 150 500 10 -10 X2 50 1 500 -5 60 560 120 MIN-DEFICIT Solución 150 x1 + 50 x 2 x2 500 x1 + 500 x 2 + D3 − E3 10 x1 − 5 x 2 − E1 − 10 x1 + 60 x 2 + D2 − E 2 ≤ 90000 ≤ 300 = 350000 = 5000 = 6000 D1 D2 D3 E1 E2 1 1 1 0 4400 10000 -1 -1 0 0 = 350000 = 5000 = 6000 E3 -1 1 ≤ 90000 ≤ 300 90000 120 350000 5000 6000 $0 <= 90000 <= 300 = 350000 = 5000 = 6000 0 Eliminamos el primer déficit de las restricciones (resultó cero) y resolvemos para la segunda prioridad: min Z = D2 7 Elaboró Dr. Eduardo Gutiérrez González D2 Horas de trab. Km de brecha Presupuesto X1 150 500 10 -10 X2 50 1 500 -5 60 560 120 MIN-DEFICIT Solución D2 D3 E1 E2 E3 1 -1 -1 1 1 4400 10000 -1 0 0 90000 120 350000 5000 6000 $4,400 <= 90000 <= 300 = 350000 = 5000 = 6000 0 En esta parte terminamos con una solución eficiente de 560 hectáreas limpiadas y 120 kilómetros para abrir brecha, sin cumplimiento de la segunda prioridad existe un déficit de 4400 refugios de 6000 que se requerían como meta. EJEMPLO 5 La administración de Alfred Franko Co; estableció las metas de participación de mercado que quiere que cada uno de los dos productos capte en sus respectivos mercados. En particular, la administración quiere que el producto 1 capte al menos el 15% de su mercado y que el producto 2 capte al menos 10% de su mercado. Se planean tres campañas publicitarias para tratar de lograr estas participaciones de mercado. Una está dirigida en forma directa al primer producto. La segunda se dirige al segundo producto. La tercera está pensada para reforzar la reputación general de la compañía y sus productos. Sean x1 , x 2 y x3 las cantidades de dinero asignadas (en millones de um) a estas campañas, respectivamente. La participación de mercado resultante (expresada como un porcentaje) de los dos productos se estima como: Porcentaje de mercado para el producto 1 = 0.5 x1 + 0.2 x3 Porcentaje de mercado para el producto 2 = 0.3 x 2 + 0.2 x3 Un total de 55 millones de um está disponible para las tres compañías publicitarias, pero la administración quiere que al menos 10 millones de um se dediquen a la tercera campaña. Si no se pueden lograr ambas metas de porcentaje de mercado, la administración considera que cada disminución de 1% en la participación de mercado de la meta es igualmente seria para los dos productos. Con esto, la administración quiere saber de qué modo asignar con mayor efectividad el dinero disponible en las tres campañas. a) Describa porqué éste problema es uno de programación lineal por metas y proporcione las expresiones cuantitativas para las metas y el objetivo global. b) Formule y resuelva éste problema. c) Interprete la solución de éste problema en el lenguaje de la administración. Solución Planteamiento del modelo. Paso 1. Definición de variables. xi = Cantidades de dinero asignadas a la campaña i ( i = 1, 2, 3 ) Paso 2. Metas 8 Investigación de Operaciones Avanzada. Sesión 7 0.5 x1 + 0.2 x3 ≥ 15% Porcentaje de mercado para el producto 1 0.3 x1 + 0.2 x3 ≥ 10% Porcentaje de mercado para el producto 2 Paso 3. Restricciones x1 + x 2 + x3 ≤ 55 um (millones) Total disponible x3 ≥ 10 um (millones) disponible para la campaña 3 Agregando los déficit y excesos por restricción 0.5 x1 + 0.2 x3 + D1 − E1 = 15 0.3 x1 + 0.2 x3 + D2 − E 2 = 10 x1 + x 2 + x3 ≤ 55 x3 ≥ 10 Paso 4. Función Objetivo min Z = D1 + D2 Paso 5. Cálculos X1 Porcentaje mercado 1 Porcentaje mercado 2 Presupuesto X2 X3 D1 0.2 0.2 1 1 0.3 1 0.5 1 Pres. campaña 3 E1 E2 -1 1 -1 1 min= Solución D2 13.333 0 41.667 1 0 1 1.667 15 10 55 = 15 = 10 <= 55 41.6667 >= 10 1.66667 0 0 Paso 6. Conclusiones La mejor solución se obtiene al dedicar 13.333 um (millones) a la campaña 1 y 41.667 um (millones) a la campaña 3. Para lo anterior se dispone de todo el capital 55 millones de um y se pasa en 31.6667 millones um para la campaña 3 EJEMPLO 6 Una fábrica elabora cuatro productos etiquetados como A, B, C y D. El comité ejecutivo está reunido para decidir sobre la mezcla de los productos. El director desea la mezcla que alcance la mayor utilidad; el gerente de ventas desea obtener la mayor participación del mercado, y el gerente de producción desea que las instalaciones de producción funcionen en equilibrio. El presidente debe mediar entre estos objetivos potencialmente conflictivos. La información sobre los cuatro productos aparece en la tabla siguiente, que muestra las horas necesarias por unidad para cada producto en ensamble y en ensayo, y el tiempo de maquinado, así como el tiempo en los departamentos 1 y 2. 9 Elaboró Dr. Eduardo Gutiérrez González Concepto Recursos: Tiempo de ensamble (horas) Tiempo de ensayo (horas) Tiempo de maquinado (horas) Departamento 1 (horas) Departamento 2 (horas) Metas: Utilidad (UM) Participación en el mercado (puntos) Producto B C D 4 2 6 1 1/2 15 2 2 2 1 5 2 10 1 2 2 1 12 *1 * 10 1 50 1 20 1 5 1 A La utilidad por unidad para cada producto también se muestra en la tabla anterior. El director piensa que la fábrica debería enfatizar en los productos B y C, ya que éstos producen la mayor utilidad por unidad, su aspiración sería obtener una utilidad de 10,000 um. El gerente de mercadotecnia considera cada producto como una venta y, por consiguiente, cuenta como un punto en la participación de mercado, es decir, que equivale a una participación de 0.01 %, su meta es de 800 puntos de participación (es decir, 8% del mercado total). El gerente de producción anota que la fábrica dispone de 3,000 horas de ensamble, 1,000 de tiempo de ensayo, y 7,500 de tiempo de maquinado. No existen límites de horas para los departamentos 1 y 2. Sin embargo, es el equilibrio de las horas trabajadas en estos departamentos lo que preocupa. Al gerente de producción le gustaría que la cantidad de horas trabajadas en los departamentos 1 y 2 fuera igual o lo más cercana posible. El presidente decidió que debe darse un peso a cada objetivo. Una utilidad de una um vale lo mismo, sin tener en cuenta sí está por encima o por debajo de la meta de 10,000 um del director. Un punto en la participación de mercado vale 10 um por debajo de la meta de 800, pero sólo 5um por encima de ésta. Una hora de desbalance de los tiempos de los departamentos de producción tiene un costo de 10 um. Formule esta situación como un problema de programación de metas. Solución. Planteamiento del modelo. Paso 1.Definición de variables. xi = Cantidad de producto manufacturado i ( i = A, B, C , D1, D 2 ), para la D son dos departamentos. Paso 2. Metas 10 x A + 50 x B + 20 xC + 5 x D1 + 5 x D 2 ≥ 10000 Utilidades x A + x B + xC + x D1 + x D 2 ≥ 800 Participación en el Mercado x A + 2 x B + xC + 2 x D1 − (0.5 x A + x B + 2 xC + 2 x D 2 ) = 0 0.5 x A + x B − xC + 2 x D1 − 2 x D 2 = 0 Tiempo balanceo de la producción 1 El producto D requiere de dos horas, pero puede fabricarse en el departamento 1 o en el departamento 2, o dividirlo entre ellos como se desee. 10 Investigación de Operaciones Avanzada. Sesión 7 Paso 3. Restricciones 4 x A + 15 x B + 5 xC + 2 x D1 + 2 x D 2 ≤ 3000 Ensamble 2 x A + 2 x B + 2 xC + x D1 + x D 2 ≤ 1000 Ensayo 6 x A + 2 x B + 10 xC + 12 x D1 + 12 x D 2 ≤ 7500 Maquinado Agregando las variables de déficit y exceso 10 x A + 50 x B + 20 xC + 5 x D1 + 5 x D 2 + D1 − E1 = 10000 x A + x B + xC + x D1 + x D1 + x D 2 + D2 − E 2 = 800 0.5 x A + x B − xC + 2 x D1 − 2 x D 2 + D3 − E3 = 0 4 x A + 15 x B + 5 xC + 2 x D1 + 2 x D 2 ≤ 3000 2 x A + 2 x B + 2 xC + x D1 + x D 2 ≤ 1000 6 x A + 2 x B + 10 xC + 12 x D1 + 12 x D 2 ≤ 7500 Paso 4. Función Objetivo: min Z = D1 + 10 D2 − 10 D3 − E1 − 5 E 2 + 10 E 3 Paso 5. Cálculos XA 10 utilidad 1 participación 0.5 balanceo 4 ENSAMBLE 2 ENSAYO 6 MAQUINADO MIN= SOLUCIÓN 0 XB 50 1 1 15 2 2 72 XC 20 1 -1 5 2 10 208 XD1 XD2 5 5 1 1 2 -2 2 2 1 1 12 12 0 D1 1 D2 D3 E1 -1 1 E2 E3 -1 1 1 10 -10 439 37.9 80.3 1015 -1 -1 0 -5 0 10 0 10000 800 0 3000 1000 7500 -9311 = = = <= <= <= 10000 800 0 3000 1000 7500 Paso 6. Conclusiones En base a los resultados se puede concluir que la opción más satisfactoria es cuando se producen 72 unidades del producto B, 208 unidades de C y 439 unidades del producto D en el departamento 2. Logrando balancear el tiempo en los dos departamentos, ya que no se tiene ningún déficit o exceso en esa parte. Con un déficit de 647 para alcanzar la meta de 10 000 y de 57.1 para alcanzar la meta de 800. EJERCICIOS 1.- Un inversionista tiene 80,000um que puede invertir en dos tipos de acciones cuyas características son: Acciones Precio(um) 1 2 25 50 Rendimiento anual estimado (um) 3 5 Índice de riesgo 0.50 0.25 El inversionista desea tener un portafolio que satisfaga: Prioridad 1: El índice de riesgo del portafolio es menor o igual a 700. 11 Elaboró Dr. Eduardo Gutiérrez González Prioridad 2: El portafolio produce un rendimiento anual no menor de 9000um. Considerando las variables de decisión xi : cantidad de acciones i compradas, para i = 1, 2 . Formule y resuelva un problema lineal para resolver la problemática de acuerdo a la primera prioridad. 2.- Una empresa desea desarrollar un portafolio de inversión para uno de sus nuevos clientes. Suponga que el cliente desea restringir la inversión a dos títulos-valor Titulo 1 2 Precio acción 50 100 Rendimiento anual estimado 6% 10% El cliente tiene 50,000um para invertir y ha establecido las siguientes metas: Prioridad 1: Obtener por lo menos 9% de rendimiento anual. Prioridad 2: Limitar la inversión en acciones del titulo 2 a no más de 60%. Formule y resuelva un problema lineal para resolver la problemática. 3.- Una fábrica elabora dos productos A y B. A continuación se muestra la contribución a la utilidad y el uso de recursos para una unidad de cada producto. Concepto Contribución a la utilidad (um por unidad Uso de recursos: Producto A 15 Producto B 10 Tiempo de la máquina (horas por unidad) Materia prima (toneladas por unidad) Mano de obra calificada (horas por unidad) Mano de obra no calificada (horas por unidad) 4 5 1 2 5 4 5 0 La fábrica dispone de un máximo de 100 horas de maquinado y 30 de mano de obra no calificado. Existe un faltante de materia prima. La fábrica recibió una asignación de 100 toneladas de su planta principal aunque con instrucciones de utilizar lo menos posible de devolver el excedente para que otras secciones puedan utilizarlo. Podría obtenerse más de las 100 toneladas asignadas, pero sólo si fuera absolutamente necesario. La fábrica tiene una fuerza calificada de 75 horas disponibles en horario normal. Estos trabajadores calificados están renuentes a trabajar tiempo extra, pero lo harán si es necesario. La gerencia desea utilizar los trabajadores capacitados durante el tiempo normal tanto como sea posible. La fábrica tiene una meta de utilidad de 300um que espera cumplir o superar. • Defina las variables de decisión y las restricciones sobre el tiempo de maquinado y de mano de obra no calificada. • Formule las restricciones de la meta (nivel de déficit y excedente), respecto a mano de obra calificada, materia prima y utilidad. 12 Investigación de Operaciones Avanzada. Sesión 7 • Resuelva el problema suponiendo que la gerencia agrega costos de 15um por tonelada a la materia prima utilizada que excede la asignación, 10um por hora extra para trabajadores calificados y 5um por hora de tiempo ocioso de esos trabajadores. Además, la materia prima no utilizada (por debajo de la asignación) tiene un valor de 5um por tonelada. Una um de utilidad tiene el mismo valor, sin tener en cuenta si excede o no la meta de utilidad. 4.- Un país en vías de desarrollo que cuenta con 15,000,000 de acres de tierra agrícola de control público en uso activo. Su gobierno está planeando una forma de dividir estas tierras el año entrante entre tres cultivos básicos (etiquetados 1, 2 y 3). Cierto porcentaje de cada cultivo se exporta para obtener capital extranjero necesario, y el resto de cada uno de estos cultivos se usa para alimentar a la población. La cosecha de estos cultivos también da empleo a una parte importante de la población. Por ello, los tres factores principales a considerar en la asignación de tierra a estos cultivos son: 1. La cantidad de capital extranjero generado en um. 2. El número de ciudadanos alimentados. 3. El número de ciudadanos empleados en cosechar estos cultivos. La siguiente tabla muestra cuánto contribuyen cada 1,000 acres de cada cultivo a estos factores y la última columna proporciona la meta establecida por el gobierno para cada uno de estos factores. Contribución por cada 1,000 acres de cultivo Factor Capital extranjero (um) 1 2 3 Meta 3,000 5,000 4,000 ≥70,000,000 Ciudadanos alimentados 150 75 100 ≥ 1,750,000 Ciudadanos empleados 10 15 12 = 200,000 Al evaluar la seriedad relativa de no lograr estas metas, el gobierno concluyó que las siguientes desviaciones de las metas deben tomarse como igualmente indeseables: 1. Cada 100um debajo de la meta de capital extranjero. 2. Cada persona debajo de la meta de ciudadanos alimentados. 3. Cada desviación de uno (en cualquier dirección) de la meta de ciudadanos empleados. a) Describa porqué el problema es uno de programación por metas y proporciones las expresiones cuantitativas para las metas y el objetivo global. b) Formule y resuelva este problema como un modelo de programación de metas. c) Formule y resuelva este problema como un modelo de programación lineal. 13