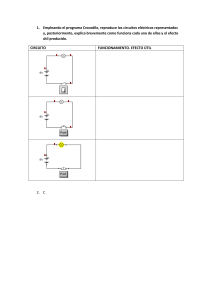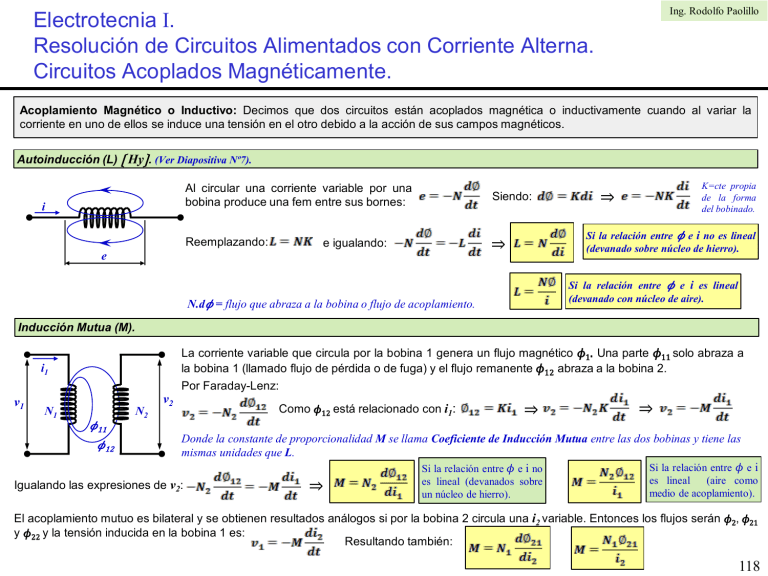
Ing. Rodolfo Paolillo Electrotecnia I. Resolución de Circuitos Alimentados con Corriente Alterna. Circuitos Acoplados Magnéticamente. Acoplamiento Magnético o Inductivo: Decimos que dos circuitos están acoplados magnética o inductivamente cuando al variar la corriente en uno de ellos se induce una tensión en el otro debido a la acción de sus campos magnéticos. Autoinducción (L) 〔 Hy〕. (Ver Diapositiva Nº7). i Al circular una corriente variable por una bobina produce una fem entre sus bornes: Siendo: Reemplazando: ⇒ e igualando: e K=cte propia de la forma del bobinado. ⇒ Si la relación entre 𝜙 e i no es lineal (devanado sobre núcleo de hierro). Si la relación entre 𝜙 e i es lineal (devanado con núcleo de aire). N.d𝜙 = flujo que abraza a la bobina o flujo de acoplamiento. Inducción Mutua (M). La corriente variable que circula por la bobina 1 genera un flujo magnético 𝜙1. Una parte 𝜙11 solo abraza a la bobina 1 (llamado flujo de pérdida o de fuga) y el flujo remanente 𝜙12 abraza a la bobina 2. Por Faraday-Lenz: i1 v1 N2 N1 v2 Como 𝜙12 está relacionado con i1: ⇒ ⇒ 𝜙11 𝜙12 Donde la constante de proporcionalidad M se llama Coeficiente de Inducción Mutua entre las dos bobinas y tiene las mismas unidades que L. Si la relación entre 𝜙 e i Si la relación entre 𝜙 e i no Igualando las expresiones de v2: ⇒ es lineal (devanados sobre un núcleo de hierro). es lineal (aire como medio de acoplamiento). El acoplamiento mutuo es bilateral y se obtienen resultados análogos si por la bobina 2 circula una i2 variable. Entonces los flujos serán 𝜙2, 𝜙21 y 𝜙22 y la tensión inducida en la bobina 1 es: Resultando también: 118 Electrotecnia I. Resolución de Circuitos Alimentados con Corriente Alterna. Circuitos Acoplados Magnéticamente. Ing. Rodolfo Paolillo Coeficiente de Acoplamiento (k). El flujo de acoplamiento depende de la separación y orientación de los ejes de las bobinas y de la permeabilidad magnética del medio. La fracción del flujo total que abraza o acopla a las dos bobinas se llama coeficiente de acoplamiento k. ⇒ Multiplicando las dos expresiones encontradas para M resulta: Por ser 𝜙12 ≤ 𝜙1 y 𝜙21 ≤ 𝜙2 ⇒ k varía entre 0 y 1 (adimensional). Si k→0 el acoplamiento magnético es débil. Si k→1 el acoplamiento magnético es fuerte. En general toda máquina eléctrica tiene un acoplamiento magnético fuerte. Tipos de Circuitos con Acoplamiento Magnético. Tipos de Circuitos Acoplados Circuitos acoplados magnéticamente y conductivamente. • Circuitos serie. • Circuitos paralelo. • Circuitos mixtos. Circuitos acoplados magnéticamente. • Transformador. • Generador. • Motor. 119 Ing. Rodolfo Paolillo Electrotecnia I. Resolución de Circuitos Alimentados con Corriente Alterna. Circuitos Acoplados Magnéticamente. Regla de los puntos para bobinas con acoplamiento magnético. L2 Si en la Fig. 1 no existiera la bobina L2 la tensión en la bobina L1 sería: L1 𝜙22 Si tenemos en cuenta la influencia de la bobina L2 debemos considerar el flujo 𝜙12: 𝜙21 𝜙12 𝜙11 El signo (+) corresponde al caso en que los flujos propios y mutuos se suman como en la Fig. 1. El signo (-) corresponde al caso de la Fig. 2 en que los flujos propios y mutuos se restan. i2 i1 B A D C Figura 1 Según lo precedente podemos escribir: L2 Análogamente, la tensión inducida en la bobina L2 resulta: L1 Podemos observar que los primeros términos de los segundos miembros son las tensiones de autoinducción mientras que los restantes son las tensiones inducidas por los flujos mutuos por lo que se los denomina tensiones de inductancia mutua: 𝜙22 𝜙12 𝜙21 𝜙11 i2 i1 Siendo: M12 = M21 =M Para tener en los esquemas circuitales la información sobre la interacción entre los flujos propios y mutuos se definen las polaridades de la siguiente forma: Se dice que dos bornes tienen igual polaridad respecto del flujo, o bien que son homólogos, cuando las corrientes entran o salen por ambos conjuntamente y crean flujos propios y mutuos que se suman. Los bornes homólogos se identifican con un punto (o identificación similar) según la Fig. 3. Figura 3 Observando la Fig. 1 y Fig. 2 el borne homólogo del B resulta el D. Análogamente en la Fig. 4 los bornes de igual polaridad respecto del flujo son B y C o bien A y D. B A D C Figura 2 L2 L1 𝜙22 𝜙21 𝜙12 𝜙11 i2 i1 A C B Figura 4 D 120 Ing. Rodolfo Paolillo Electrotecnia I. Resolución de Circuitos Alimentados con Corriente Alterna. Circuitos Acoplados Magnéticamente. Signo de la tensión de inducción mutua en el planteo de ecuaciones. Aplicando la regla de los puntos vista podemos concluir: 1.- Si las dos corrientes consideradas entran o salen de las bobinas acopladas por los bornes homólogos, los signos de los términos en M son los mismos que los signos de los términos en L. 2. Si una corriente entra por un borne con punto y la otra sale por el otro borne con punto, los signos de los términos en M son opuestos a los signos de los términos en L. Términos M y L: signos iguales. Términos M y L: signos opuestos. Análisis de Circuitos con acoplamiento magnético. + jωL1 I1 - + R1 L1 I1 V - + jωM I2 - jωL2 I2 + - + v R2 - jω L2 I1 jωM I1 L2 + jωL1 I1 jωM I1 + L1 - i - I2 R2 L2 - R1 + Ejemplo 2: Circuito con acople magnético solamente. M Ejemplo 1: Circuito con acople magnético y conductivo. M + El método de mallas es el más apropiado y seguimos los siguientes pasos: 1) Elegimos arbitrariamente el sentido de corriente en cada malla. 2) Indicamos las tensiones de autoinducción sabiendo que producen tensiones con la polaridad positiva en el borne por donde entra la corriente. 3) Indicamos las tensiones de inductancia mutua con el criterio de puntos. 4) Planteamos las ecuaciones según la LKT para cada malla. Sabiendo que: + jωM I1 Planteado directamente con valores eficaces: i = Imax sen ωt = Imax e j0 (di /dt) = Imax ω cos ωt = Imax ω e j90 Pasamos a valores eficaces y resulta: V = I1 R1 + jωL1 I1 – jωM I2 V = I R1 + jωL1 I + jωM I + I R2 + jωL2 I + jωM I 0 = I2 R2 + jωL2 I2 – jωM I1 V = I (R1 + R2 )+ j ω I (L1+ L2 + 2M) 121 Ing. Rodolfo Paolillo Electrotecnia I. Resolución de Circuitos Alimentados con Corriente Alterna. Circuitos Acoplados Magnéticamente – Acople magnético y conductivo. Circuito Serie. Según vimos en el Ejemplo 1 anterior: R1 M L1 R2 Circuito Eléctrico Equivalente. Teniendo en cuenta 1 podemos escribir: L2 Bobina 1 Bobina 2 i V = I R1 + j ω I (L1 ± M) + I R2 + j ω I (L2 ± M) 1 v - + A esta ecuación corresponde el circuito eléctrico equivalente siguiente: R1 L1 ± M R2 L2 ± M Resultando entonces: Diagramas fasoriales. Caso Aditivo j I R1 j I VS Real 2 jXM ZA j X L2 φA R1 - 2 I jωM I jω L1 I R2 j X L1 R2 Real + j I jω L2 φA v Caso Sustractivo 2 I jωM VA i I jω L1 φs I R1 I jω L2 I R2 I - Determinación de M en base al circuito RL. Considerando el caso M aditivo circulará I1: Para el caso M sustractivo tendremos I2: Real j j X L2 - 2 jXM ZS R1 j X L1 φs R2 Real Restando ambas expresiones y despejando M: Conociendo los parámetros del circuito y midiendo I1 e I2 se obtiene M. 122 Ing. Rodolfo Paolillo Electrotecnia I. Resolución de Circuitos Alimentados con Corriente Alterna. Circuitos Acoplados Magnéticamente – Acople magnético y conductivo. Circuito Paralelo. I I1 + I2 R1 R2 La impedancia total valdrá: Sin acople ⇒ Z12= 0 (paralelo tradicional). v - La impedancia de cada rama será: L2 L1 M Para el caso general, por Kirchhoff tenemos: jI2 ωL2 Caso M Sustractivo Caso M Aditivo V V Expresado en forma fasorial: I1 R1 jI2 ωM jI2 ωM jI1 ωM Tomando las ecuaciones 2 y 3 y reagrupando calculamos las corrientes: jI2 ωL2 jI1 ωL1 I2 R2 jI1 ωL1 I1 I2 R2 jI1 ωM I1 R1 I1 I2 I2 I I 123 Ing. Rodolfo Paolillo Electrotecnia I. Resolución de Circuitos Alimentados con Corriente Alterna. Circuitos Acoplados Magnéticamente – Acople magnético y conductivo. Circuito Paralelo – Circuito eléctrico equivalente - Caso M Aditivo. Podemos interpretar y dibujar el circuito anterior de la siguiente forma: Regla de la mano derecha. I 𝛷1 I2 I1 𝛷M L1 + I L2 v - I1 + I2 R1 R2 v 𝛷M R1 𝛷2 - L2 L1 R2 M En base a las ecuaciones vistas podemos encontrar un circuito puramente eléctrico que sea equivalente al circuito eléctrico con acoplamiento magnético analizado. Para tal fin sumamos y restamos términos convenientemente como se muestra a continuación: I2 I + V - I1 124 Ing. Rodolfo Paolillo Electrotecnia I. Resolución de Circuitos Alimentados con Corriente Alterna. Circuitos Acoplados Magnéticamente – Acople magnético y conductivo. Circuito Paralelo – Circuito eléctrico equivalente - Caso M Sustractivo. Análogamente al caso anterior: Regla de la mano derecha. I 𝛷1 I2 I1 𝛷2 L1 + L2 v - I I1 + I2 R1 R2 v 𝛷M R1 𝛷M - L2 L1 R2 M En base a las ecuaciones vistas podemos encontrar un circuito puramente eléctrico que sea equivalente al circuito eléctrico con acoplamiento magnético analizado. Para tal fin sumamos y restamos términos convenientemente como se muestra a continuación: I2 I + V - I1 Conclusión: en caso de acoplamiento aditivo si ZM es mayor que Z1, ó ZM es mayor que Z2 (o sea M > L1 ó M > L2 ) la rama podrá tener características capacitivas, efecto que no puede ocurrir en el acoplamiento sustractivo donde las ramas son siempre inductivas (si M < L1 ó M < L2 ). 125 Ing. Rodolfo Paolillo Electrotecnia I. Resolución de Circuitos Alimentados con Corriente Alterna. Circuitos Acoplados Magnéticamente – Acople magnético y conductivo. Circuito Serie – Paralelo. Para resolver este caso utilizaremos el método de las Leyes de Kirchhoff planteando las correspondientes ecuaciones para el nodo A y las mallas I y II: M13 R1 L1 i1 M12 + - i3 M23 L2 I v R3 L3 A i2 Nodo A: Malla I: II Caída en L1 Malla II: R2 Caída en L2 Caída en L2 Caída en L3 Escribimos las ecuaciones en forma fasorial y las agrupamos por incógnitas: Z1 Z2 Z4 Z5 Z3 Z6 Reemplazando las impedancias en las ecuaciones hallamos las corrientes: ⇒ 126 Ing. Rodolfo Paolillo Electrotecnia I. Resolución de Circuitos Alimentados con Corriente Alterna. Circuitos Acoplados Magnéticamente – Acople magnético y conductivo. Circuito Serie – Paralelo – Circuito Eléctrico Equivalente. El sistema de ecuaciones lo podemos agrupar de la siguiente forma: 1 Siendo: 2 3 Reemplazando en 2 y teniendo en cuenta 1 : Reemplazando en 3 y teniendo en cuenta 1 : El circuito eléctrico equivalente que cumple con las ecuaciones precedentes es el siguiente: ZA ZC I1 I3 + V I2 ZB - 127 Electrotecnia I. Resolución de Circuitos Alimentados con Corriente Alterna. Circuitos Acoplados Magnéticamente – Acople inductivo solo. R1 Hallamos el valor de las corrientes mediante la regla de Cramer: M i2 i1 + (I) - R2 L2 L1 v Ing. Rodolfo Paolillo (II) 𝛷M ZTeq Al circular i1 por L1 produce un flujo que genera en L2 una fem. Como el circuito está cerrado a través de R2 circulará una corriente i2 que genera en L2 un flujo que se opone a la causa que la produce (Faraday-Lenz ). En consecuencia podemos afirmar que el flujo mutuo no refuerza al flujo propio por lo que las fem producidas por L y M serán opuestas. La impedancia total equivalente del circuito será: Por LKT resulta: Racionalizando: Planteado con valores eficaces: Si M = 0 resulta: I1 = V / Z11 y Z12 = Z21 = 0 e I2 = 0. El acoplamiento magnético aumenta la parte real y disminuye la imaginaria del circuito primario. 128 Ing. Rodolfo Paolillo Electrotecnia I. Resolución de Circuitos Alimentados con Corriente Alterna. Circuitos Acoplados Magnéticamente – Acople inductivo solo. Circuito con acoplamiento inductivo solo – Circuito Eléctrico Equivalente. Buscamos un circuito puramente eléctrico, como el dibujado a continuación, que sea equivalente al circuito acoplado original. Esta consideración será de mucha utilidad, por ejemplo, en el análisis de máquinas eléctricas: Reemplazando en el circuito queda finalmente: ZA R1 ZA V I2 ZC - R2 L2 - M ZB I1 + ZB L1 - M Por mallas resulta: Recordando el sistema de ecuaciones obtenido para el circuito acoplado original: (1) + I2 I1 V M ZC - En caso de acoplamientos fuertes puede ser que M > L1 o que M > L2 , entonces el término será negativo y la impedancia actúa como capacitiva. Trazamos el diagrama fasorial tomando como referencia, por ejemplo, a I2 y representamos el sistema de ecuaciones del circuito (1): I2 jωL2 - I1 jωM Por comparación entre ambos sistemas resulta: I2 R2 I2 I1 jωL1 Operando: V - I2 jωM I1 R1 I1 129 Ing. Rodolfo Paolillo Electrotecnia I. Resolución de Circuitos Alimentados con Corriente Alterna. Circuitos Acoplados Magnéticamente – Fuentes en ambos circuitos. Consideremos el siguiente circuito: 𝛷1 R1 + i1 R1 R2 i1 + i2 i2 L2 v1 v2 - - + + L2 L1 v1 L1 R2 M Regla de la mano derecha. v2 𝛷2 - - Por LKT: ⇒ Planteando otro ejemplo: V1 + V1 - L1 R1 - L2 L1 L2 + V2 (II) - M R1 V2 C (I) - 𝛷1 + I2 I1 + I2 I1 R2 Por LKT: 𝛷2 R2 Regla de la mano derecha. Finalmente: 130