Funciones

Unidad
5
Patricio Retamal Lizana
Álgebra
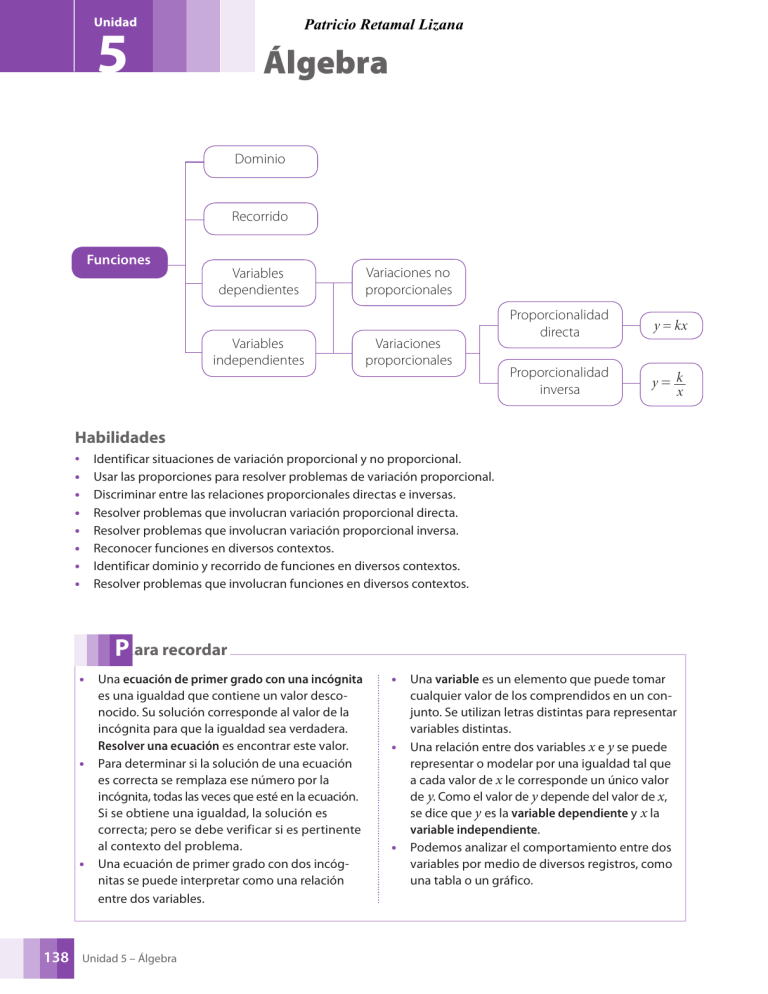
Dominio
Recorrido
Funciones
Variables
dependientes
Variables
independientes
Variaciones no
proporcionales
Variaciones
proporcionales
Proporcionalidad
directa
y = kx
Proporcionalidad
inversa
y= k
x
Habilidades
• Identificar situaciones de variación proporcional y no proporcional.
•
•
•
•
•
•
•
Usar las proporciones para resolver problemas de variación proporcional.
Discriminar entre las relaciones proporcionales directas e inversas.
Resolver problemas que involucran variación proporcional directa.
Resolver problemas que involucran variación proporcional inversa.
Reconocer funciones en diversos contextos.
Identificar dominio y recorrido de funciones en diversos contextos.
Resolver problemas que involucran funciones en diversos contextos.
P ara recordar
• Una ecuación de primer grado con una incógnita
•
•
138
es una igualdad que contiene un valor desconocido. Su solución corresponde al valor de la
incógnita para que la igualdad sea verdadera.
Resolver una ecuación es encontrar este valor.
Para determinar si la solución de una ecuación
es correcta se remplaza ese número por la
incógnita, todas las veces que esté en la ecuación.
Si se obtiene una igualdad, la solución es
correcta; pero se debe verificar si es pertinente
al contexto del problema.
Una ecuación de primer grado con dos incógnitas se puede interpretar como una relación
entre dos variables.
Unidad 5 – Álgebra
• Una variable es un elemento que puede tomar
•
•
cualquier valor de los comprendidos en un conjunto. Se utilizan letras distintas para representar
variables distintas.
Una relación entre dos variables x e y se puede
representar o modelar por una igualdad tal que
a cada valor de x le corresponde un único valor
de y. Como el valor de y depende del valor de x,
se dice que y es la variable dependiente y x la
variable independiente.
Podemos analizar el comportamiento entre dos
variables por medio de diversos registros, como
una tabla o un gráfico.
Patricio Retamal Lizana
• Una función es una relación entre dos variables
x e y, de manera que a cada valor de x le corresponde un único valor de y.
• Una función se puede representar o modelar de
•
•
•
•
•
•
•
diversas formas; por ejemplo, con una ecuación,
una tabla de valores o un gráfico.
Para representar una función en un gráfico,
los valores de la variable independiente se
representan sobre el eje horizontal o de las
abscisas, y los valores de la variable dependiente
se representan sobre el eje vertical o de
las ordenadas.
La variable y puede también escribirse como
f (x ) donde x es la otra variable, y se lee “f de x”.
Se llama dominio de una función al conjunto de
valores que la variable independiente x puede
tomar en la función f. Se expresa por Dom(f ).
Se llama recorrido de una función al conjunto de
valores que toma la variable dependiente y, es
decir, todos los valores que resultan al remplazar
los valores del dominio en la función f. Se expresa
por Rec(f ).
Un valor constante es una cantidad que tiene un
valor fijo, que no se modifica en una situación dada.
Una razón es una comparación entre dos cantidades que se realiza por medio de una división.
El valor de la razón es el cociente entre las cantidades. Dos razones son equivalentes si su valor
es el mismo.
• Una proporción es una igualdad entre dos o más
razones. La proporción entre las cantidades a, b,
c y d se puede expresar a : b = c : d, o bien a = c
b d
y se lee “a es a b, como c es a d”.
• En toda proporción se cumple que a = c , si y
b d
solo si a · d = b · c.
• Un porcentaje se escribe, por ejemplo, a %, y
se lee “a por ciento”. El porcentaje es una razón
•
• Una relación de proporcionalidad directa se puede representar como una función de la forma
y = kx. La representación gráfica de esta función
son puntos que pertenecen a una misma recta
que pasa por el origen en un sistema de coordenadas cartesianas. Por ejemplo, el gráfico de la
función y = x es:
• En una función de proporcionalidad directa,
•
si una de las variables aumenta, la otra también
aumenta en un mismo factor; y si una de las
variables disminuye, la otra también disminuye
en un mismo factor.
Dos variables, una independiente x y la otra
dependiente y, son inversamente proporcionales
si el producto entre ellas se mantiene constante,
es decir, x · y = k, donde k es la constante de
proporcionalidad.
• Una relación de proporcionalidad inversa se
puede representar como una función de la
forma y = k . La representación gráfica de
x
esta función son puntos que forman una curva
llamada hipérbola. Por ejemplo, el gráfico de la
función y = 1 es:
x
cuyo consecuente es 100.
Si el valor de la razón entre dos variables se
mantiene constante (no cambia) estas variables
son proporcionales.
• Dos variables, una independiente x y la otra
dependiente y, son directamente proporcionales si
el valor de la razón y es constante, es decir, y = k,
x
x
donde k es la constante de proporcionalidad.
• En una relación de proporcionalidad inversa, si
una de las variables aumenta, la otra disminuye
en un mismo factor; y si una de las variables
disminuye, la otra aumenta en un mismo factor.
Unidad 5 – Álgebra
139
Patricio Retamal Lizana
Relación entre dos variables
Ejercicios resueltos
1. Pablo camina desde su casa al colegio y avanza 2 cuadras cada 5 minutos. Si el colegio queda a 8 cuadras y
Pablo camina manteniendo el mismo ritmo, ¿cuánto demora en llegar?
Podemos hacer una tabla que relacione las cuadras (c) que avanza y el tiempo (t) que
demora en llegar a su colegio.
En la tabla observamos que Pablo tarda 15 minutos en llegar.
2. En la pregunta anterior, escribe una ecuación que relacione las variables.
Como Pablo avanza 2 cuadras en 5 minutos, tarda 2,5 minutos en caminar 1 cuadra.
Si llamamos c a las cuadras y t al tiempo, la ecuación que relaciona las cuadras que
recorre Pablo y el tiempo que tarda es t = 2,5c.
c
t
2
5
4
10
8
15
3. En la ecuación 3x + 2y = 4, encuentra los valores de x cuando y vale 1 y 2, y los valores de y cuando x vale 0
y 1. Realiza una tabla que registre los valores que obtuviste.
Si y = 1, remplazamos 3x + 2 · 1 = 4. Luego, despejamos x :
3x = 4 – 2 = 2, entonces x = 2 .
3
Si y = 2, remplazamos 3x + 2 · 2 = 4. Luego, despejamos x :
3x = 4 – 4 = 0, entonces x = 0.
Si x = 0, remplazamos 3 · 0 + 2y = 4. Luego, despejamos y:
2y = 4, entonces y = 4 = 2.
2
Si x = 1, remplazamos 3 · 1 + 2y = 4. Luego, despejamos y:
2y = 4 – 3 = 1, entonces y = 1 .
2
x
y
2
3
1
0
2
0
2
1
1
2
Ejercicios y problemas propuestos
1. Cada una de las siguientes tablas muestra la
relación entre dos variables. Identifica cuáles son
esas variables y determina la unidad en la que se
encuentran definidas, si corresponde.
a.
c.
Días de
marzo
Ventas
($)
Pan
(kg)
Dinero
($)
1
412 000
1
5 000
2
320 000
2
8 200
3
120 000
3
5 600
b.
d.
Tiempo
(h)
Velocidad
(km/h)
X
Y
2
–5
5
100
3
4
6
120
7
2
12
50
2. Si a = 2b:
a. completa la tabla.
b. despeja b en la ecuación.
c. inventa una relación entre dos
variables que pueda cumplir
con la ecuación a = 2b.
Unidad 5 – Álgebra
b
–8
0,5
13
7
3. Si y = x – 3:
a. elabora una tabla donde x tome los valores
{2, 4, 7, 10}
b. despeja x en la ecuación.
c. encuentra el valor de x si y = 12.
4. Encuentra cada uno de los valores señalados en
las siguientes ecuaciones con dos variables.
a. 5y = 3x
• Si x = 0,2 encuentra el valor de y.
•
Si y = 15 encuentra el valor de x.
b. 3x – 2 = y
• Si x = –8 encuentra el valor de y.
•
140
a
Si y = 27 encuentra el valor de x.
5. Si 4x + 2y = 17, el valor de y si x = 1 es:
4
A. y = 4
B. y = 8
C. y = 9
D. y = 10
6. Despeja en las ecuaciones la variable indicada.
a. Despeja y en x = –2y.
b. Despeja x en y = 7 + x.
c. Despeja x en y = 12 – x.
d. Despeja y en 2x = 3y.
e. Despeja y en x = y .
2
x
f. Despeja x en = y .
8 3
g. Despeja x en x + 5 – y = 0.
7. Al despejar la variable x en la ecuación
5x + 2y = 2, se obtiene:
A. x = 2 + 2y
5
B. x = 7 – 2y
C. x = 2 – 2y
5
2
y
–2
D. x =
5
8. La edad de Alejandro (a) y la edad de su hermano
Andrés (h) se relacionan mediante la ecuación
a – h = 1,5.
a. ¿Cómo interpretas esta ecuación?
b. Realiza una tabla con las edades de los
hermanos en cuatro años distintos.
9. Si Andrea es 3 años mayor que Javier, ¿cuál es
la ecuación que relaciona sus edades? Marca la
opción correcta.
A. a – j = 3
B. a – j = 4,5
C. 3a – j = 1,5
D. a – 3j = 1,5
10. La relación que se da entre los asistentes (a) a
una obra de teatro y los ingresos de dinero (i)
es i = 3 500a.
a. Calcula los ingresos si asisten 280 espectadores
a la obra.
b. Calcula cuántos espectadores asistieron si los
ingresos fueron $ 770 000.
c. ¿Qué significa el número 3 500 en la ecuación?
11. En la pregunta anterior, si el precio de las entradas
baja un 50 %, los ingresos que se obtienen si
asisten 280 personas son:
A. $ 350 000
B. $ 490 000
12. El perímetro de un cuadrado se calcula a partir de
la fórmula P = 4a, donde P es el perímetro y a la
medida del lado.
a. Despeja el valor de a.
b. Calcula el perímetro de un cuadrado cuyo
lado mide 7 cm.
c. ¿Cuál es la medida del lado de un cuadrado
cuyo perímetro es 36 cm?
Unidad 5
Patricio Retamal Lizana
13. La cantidad de diagonales que se pueden trazar
desde un vértice de un polígono de n lados se
calcula restando 3 al número de lados del polígono.
a. Completa la afirmación:
El número de lados de un polígono se puede
calcular sumando 3 al
.
b. Escribe una ecuación que te permita calcular
el número de diagonales (d ) por vértice, conociendo el número (n ) de lados de un polígono.
c. Escribe una ecuación que te permita calcular el
número de lados de un polígono, conociendo
las diagonales que se pueden trazar desde
un vértice.
14. ¿Cuántas diagonales se pueden trazar desde un
vértice, en un polígono de 7 lados?
A. 7 diagonales.
B. 4 diagonales.
C. 10 diagonales.
D. 9 diagonales.
15. En la sala de clases de 8º básico se realiza una
prueba. Hay 3 profesores de pie cuidando y en
cada banco se sientan 2 alumnos.
a. Si hay 11 bancos ocupados completamente,
¿cuántas personas hay en la sala de clases?
b. Realiza una tabla que relacione la cantidad de
bancos que están ocupados completamente
en la sala si hay 7, 9 y 11 personas en la sala.
c. Escribe una ecuación que relacione la cantidad de personas (p) que hay en la sala con el
número de bancos (b).
16. Si en la situación anterior se cambia a 4 el
número de personas sentadas en cada banco,
la ecuación que relaciona la cantidad de
personas (p) con el número de bancos (b) es:
A. p = 4b + 3
B. p = 2b + 4
C. p = 2b + 7
D. b = 4p + 3
C. $ 420 000
D. $ 500 000
Unidad 5 – Álgebra
141
Patricio Retamal Lizana
Funciones, variables dependientes e independientes
Ejercicios resueltos
1. Paulina quiere contratar un plan para su teléfono celular. Con el plan que le interesa puede hablar 90 minutos
por un cargo fijo de $ 12 990. Además, por cada minuto adicional se cobra un valor de $ 150. Realiza una
tabla con lo que tiene que pagar Paulina si habla 1, 2, 3, 4, 5 y 6 minutos adicionales.
Minutos
1
2
3
4
5
6
Total a pagar
13 140
13 290
13 440
13 590
13 740
13 890
2. En el problema anterior, ¿cuál es la variable independiente y cuál, la dependiente?
Como el total a pagar cambia según los minutos adicionales que se hablen, los minutos corresponden a la variable
independiente y el total a pagar a la variable dependiente.
3. Escribe una función que exprese el dinero que debe pagar Paulina según los minutos adicionales que hable.
Primero designamos variables. A los minutos adicionales que hable los llamaremos m y al total que debe pagar
lo designamos por p. Como p es la variable dependiente y m la independiente, escribimos p (m).
p (1) = 13 140 = 12 990 + 150 · 1
p (2) = 13 290 = 13 990 + 150 · 2
p (3) = 13 440 = 12 990 + 150 · 3
p (4) = 13 590 = 12 990 + 150 · 4
p (5) = 13 740 = 12 990 + 150 · 5
p (6) = 13 890 = 12 990 + 150 · 6
Podemos deducir que la función buscada es p(m) = 12 990 + 150 · m
Ejercicios y problemas propuestos
1. Considera la ecuación a = –2b + 1 y responde:
a. ¿Cuántas variables tiene?, ¿cuáles son?
b. ¿Cuál es la variable dependiente?, ¿por qué?
c. ¿Cuál es la variable que está descrita en
función de otra?
2. Considera la función de la tabla y responde.
x
y
1
3
2
5
3
7
4
5
a. ¿Cuáles son los elementos que forman el
dominio de esta función?
b. ¿Cuáles son los elementos que forman el
recorrido de esta función?
c. ¿Cuál es la imagen de 3?
d. ¿Hay algún elemento en el dominio que tenga
dos imágenes?, ¿cuál?
142
Unidad 5 – Álgebra
3. Determina si las siguientes relaciones son o
no funciones.
a.
x
y
2
b.
x
y
3
1
2
2
4
2
3
3
5
3
3
4
6
4
5
4. Relaciona y completa. Guíate por el ejemplo.
Si a = 2b + 7 decimos que a está en función de b.
En símbolos: a = f (b), o f (b) = 2b + 7
a. Si c = d – 21 decimos que
está en función
de
. En símbolos:
= f( ) o
f( ) =
.
b. Si x = 3y – 15 decimos que
está en función
de
. En símbolos:
= f( ) o
f( ) =
.
c. Si z = 9v decimos que
está en función de
. En símbolos:
= f( ) o f( ) =
.
5. Escribe en notación de funciones cada una de las
siguientes expresiones con dos variables.
a. r = 2t – 5
b. v = 3(x + 8)
c. z = 5 – w
d. 3m = 5(n – 1)
e. 4x + 5y = 2y – 2
f. 4 + a = 2b + 5
6. Sobre la expresión y = 5x + 2, ¿cuál es la afirmación
falsa? Marca la opción correcta.
A.
B.
C.
D.
Esta relación no es función.
La variable dependiente es y.
La variable independiente es x.
y está en función de x.
7. Determina si las siguientes relaciones son o
no funciones.
a. El volumen de un cubo y la longitud de una
de sus aristas.
b. Un número y su antecesor.
c. La edad que cumple una persona en cierto año.
d. El tamaño del ser humano y su edad.
8. Determina el recorrido de las siguientes funciones,
sabiendo que su dominio es el conjunto {0, 1 ,3 ,7 ,9}.
a. f (x) = 7x
b. f (x) = –2x + 3
c. f (x) = 8
d. f (x) = 3(x – 5)
9. Andrea tiene para vender 70 chocolates.
La ganancia que obtiene se puede calcular
mediante la función g (c) = 150c – 300, donde c
representa la cantidad de chocolates vendidos.
a. ¿Cuál es el dominio de la función?
b. ¿Cuál es el recorrido de la función?
c. ¿Cuántos chocolates debe vender Andrea
como mínimo para obtener ganancias?
d. ¿Qué puede significar el número 300 en la
función que representa la ganancia?
10. En la pregunta anterior, si Andrea vende todos
los chocolates, ¿cuánto dinero gana? Marca la
opción correcta.
A. $ 45 000
B. $ 21 000
C. $ 10 500
D. $ 10 200
11. Determina el recorrido de cada función.
a. El recorrido de la función f (x) = x + 8, sabiendo
que su dominio son los números pares mayores que 5 y menores que 15.
b. El recorrido de la función f (x) = x + 6, sabiendo
3
que el dominio está formado por los múltiplos
de 3 menores que 30 y mayores o iguales que 15.
12. ¿Cuál de las siguientes funciones puede tener
como dominio el conjunto {0, 1, 2 , 3, 4} y como
recorrido el conjunto {3, 5, 7 , 9, 11}?
A. f (x) = 2x + 3
C.
B. f (x) = x – 3
2 2
D.
Unidad 5
Patricio Retamal Lizana
f (x) = 11 – x
f (x) = – x + 11
2
2
13. En una piscina hay 36 000 L de agua y se empieza
a vaciar a razón de 10 litros por minuto.
a. Escribe una función que relacione la
cantidad (c) de agua que se evacua y el
tiempo (t) que se demora en hacerlo.
b. ¿Cuál es el dominio y recorrido de la función?
14. Con la información del problema anterior, ¿cuántos
litros se vaciaron en 15 horas?
A. 9 000 litros.
B.
150 litros.
C. 900 litros.
D. 1 500 litros.
15. A partir de los datos del problema 13, ¿cuánto
tiempo debe pasar para que quede la mitad de
agua en la piscina?
A. 1 200 minutos.
B. 1 800 minutos.
C. 3 600 minutos.
D. 4 800 minutos.
16. Una secuencia de números se forma considerando
la relación N = 2P + 7, donde P es la posición que
tiene el número en la secuencia y N es el número.
a. ¿Cuál es el número que se encuentra en el
lugar 12?
b. ¿En qué posición de la secuencia se encuentra
el número 43?
c. Escribe los primeros 5 números de la sucesión.
17. A partir del ejercicio anterior, ¿cuál es la expresión
que representa a los números que se encuentran
en las posiciones pares de la secuencia?
A. 2N = 2P + 7
B. N = 4P + 7
C. N = 2P + 9
D. N = 4P + 9
18. En la asignatura de Matemática, el profesor divide
un trabajo en dos partes: una prueba y una tarea
grupal. La nota que va al libro se calcula con el
promedio de la nota de la prueba y la tarea grupal.
a. ¿Cuántas variables puedes ver en esta
situación? Identifica y escribe las variables, indicando si son dependientes o independientes.
b. Escribe una función que permita calcular la
nota que puede obtener un alumno en el
trabajo de Matemática.
c. ¿Qué puedes concluir respecto de la cantidad
de variables en una función?
Unidad 5 – Álgebra
143
Patricio Retamal Lizana
Relación de proporcionalidad directa
Ejercicios resueltos
1. Si x e y varían en forma directamente proporcional y x = 3 cuando y = 8, encuentra el valor de y si x = 9.
Podemos calcular la constante de proporcionalidad:
k= 8
Escribimos la función de proporcionalidad directa.
3
y= 8 x
Remplazamos el valor de x y simplificamos.
3
y = 8 · 9 = 24
3
Otra manera de resolverlo es igualando las razones:
y=8=y
Usamos la propiedad fundamental de las proporciones.
x 3 9
3y = 8 · 9
Despejamos el valor de y.
8
·
9
y=
Simplificamos.
3
y = 24
2. En un pueblo hay 3 hombres por cada 4 mujeres. Escribe la función que permite determinar la cantidad de
hombres en función de la cantidad de mujeres.
El dato del problema indica que la razón entre hombres y mujeres es 3 : 4, por lo tanto, podemos usar una función
de proporcionalidad directa para saber la cantidad de hombres (y) en función de la cantidad de mujeres (x).
Sabemos que y = 3 , entonces y (x) = 3 x es la función buscada.
4
x 4
Ejercicios y problemas propuestos
1. Cristián tiene $ 400 y su hermana Belén, $ 200.
Su madre empieza a darles $ 200 mensuales a
cada uno.
a. Completa la tabla con la cantidad de dinero
que llevan ahorrado Cristián y Belén.
Mes
1
2
Cristián
600
800
Belén
400
3
4
5
b. La cantidad de dinero que tiene Cristián, ¿es
proporcional a la que tiene Belén? Justifica.
2. ¿Qué situación no corresponde a una relación de
proporcionalidad directa? Marca la opción correcta.
A. La distancia que recorre un auto en un cierto
tiempo cuando va a 60 km/h.
B. La diferencia de edad de dos hermanos es
cinco años.
C. Para preparar una taza de arroz se necesitan
tres tazas de agua.
D. Realizar la maqueta de una casa, usando
medidas a escala.
144
Unidad 5 – Álgebra
3. Si y es 12 cuando x es 6 y x es directamente
proporcional a y, ¿cuál es el valor de x si y es 6?
Marca la opción correcta.
A. 24
B. 12
C. 4
D. 3
4. Si y = 4 calcula el valor de x en cada caso.
a. x = 5
d. 115 = x
49
y 3
y
b. x = y
e. 164 = y
78
4 9
x
76
y
x
y
c.
=
f.
=
y x
8 6
5. Si x varía de manera directamente proporcional
a y, calcula los valores pedidos, considerando que
si y es 15 entonces x es 6.
a.
b.
c.
d.
Calcula x si y es 5.
Calcula y si x es 3.
Calcula x si y es 15.
Calcula y si x es 1.
e.
f.
g.
h.
Calcula y si x es 4.
Calcula x si y es 20.
Calcula y si x es 30.
Calcula x si y es 69.
6. En un establo, 3 caballos comen 5 fardos de
alfalfa. Si cada caballo come la misma cantidad,
¿cuántos fardos de alfalfa comerán 45 caballos?
Marca la opción correcta.
A. 75 fardos.
B. 27 fardos.
C. 9 fardos.
D. 3 fardos.
7. Escribe una función que relacione las variables en
cada caso.
a. a varía directamente con b. Cuando a es 4,
b es 5.
b. z es directamente proporcional a x. Cuando
z es 18, x es igual a 12.
c. r y s son directamente proporcionales y el valor
de su razón es 36.
8. En un estudio se obtuvo que 1 de cada 3 niños
es obeso, una función de proporcionalidad que
relaciona la cantidad de niños (n) con la cantidad
de niños obesos (o) es:
A. n = o
C. n = o
3
B. o = 3n
D. o = n
3
9. Don Pedro vende huevos a $ 110 cada uno y a
$ 600 la caja de 6. Sigue los pasos para graficar,
usando un computador, la función que modela
la ganancia ( g) que tiene don Pedro al vender
una cantidad (n) de huevos.
1º En un computador, abre una planilla de cálculo
y en la celda “A1” escribe “ganancia”.
2º En la primera columna, bajo la celda “ganancia”,
escribe los valores correspondientes a la venta
de los huevos. Esto se puede realizar fácilmente, escribiendo 110 en la celda “A2”, el número
220 en la celda “A3”; luego, selecciona ambas
celdas y con el cursor en la esquina inferior derecha de la celda “A3” lo arrastras hasta llegar a
la celda “A61”.
3º Selecciona las celdas escritas y ubica la pestaña
“Insertar”, opción gráfico. En las opciones de
gráficos, busca “Línea”.
a. Sigue los mismos pasos para realizar un gráfico
a partir de la venta de 10 cajas de 6 huevos
(60 huevos). Para ello calcula el valor de cada
huevo al vender una caja de 6 huevos.
b. Compara la inclinación de ambos gráficos y
relaciónala con las ganancias que se obtienen.
10. El rendimiento de cierto auto en carretera es 11 km
por litro, lo que se refleja en la siguiente tabla.
b (L)
Unidad 5
Patricio Retamal Lizana
d (km)
1
11
5
55
10
110
a. Identifica las variables de la situación.
b. Determina cuál es la variable independiente
y cuál es la dependiente.
c. ¿Cuál es la constante de proporcionalidad?
d. Escribe una función que relacione las variables
del problema.
e. Calcula la distancia que puede recorrer
el auto con 2, 11, 30 y 50 litros de bencina.
f. Calcula cuántos litros de bencina necesita
para recorrer:
• 11 km
• 220 km
• 1 km
• 7 km
11. En la pregunta anterior, si el litro de bencina
cuesta $ 700, ¿qué costo en bencina tiene viajar
154 km? Marca la opción correcta.
A. $ 9 600
B. $ 9 800
C. $ 10 000
D. $ 10 700
12. A partir de las preguntas anteriores, ¿cuál es el
costo aproximado de viajar desde Osorno hasta
Puerto Montt si la distancia entre estas ciudades
es de 109 km? Marca la opción correcta.
A. $ 4 900
B. $ 6 300
C. $ 7 000
D. $ 7 700
13. Juan vende helados y gana $ 150 por cada helado
que vende.
a. Completa la siguiente tabla:
Helados vendidos
Ganancia ($)
10
15
20
30
b. Escribe la función de proporcionalidad
correspondiente a la situación.
c. Calcula el valor de la constante de proporcionalidad k.
d. Interpreta el significado de la constante k.
e. Si Juan ganó $ 24 000, ¿cuántos helados vendió?
Unidad 5 – Álgebra
145
Patricio Retamal Lizana
Relación de proporcionalidad inversa
Ejercicios resueltos
1. Si x e y varían en forma inversamente proporcional y x = 3 cuando y = 8, encuentra el valor de y si x = 9.
Podemos calcular la constante de proporcionalidad:
k = 8 · 3 = 24
Remplazamos en la función de proporcionalidad.
24
y= x
Remplazamos x = 9 y simplificamos.
y = 24 = 8
9
3
Otra manera de resolverlo es igualando los productos:
9·y=8·3
Calculamos.
9y = 24
y = 24 = 8
9
3
Despejamos y y simplificamos.
2. Don Fermín quiere hacer una huerta rectangular de 720 m2. Escribe tres posibles dimensiones de la huerta
de don Fermín.
Como la huerta debe ser rectangular y su área será de 720 m2, el producto de las medidas
a (m)
l (m)
1
720
dar valores del ancho, que permitirán encontrar valores del largo. Por ejemplo:
2
360
Si a = 1, entonces l = 720.
3
240
del largo (l ) por el ancho (a) debe ser igual a 720, o sea, l · a = 720, lo que podemos
escribir como la función l(a) = 720 . Para encontrar 3 posibles dimensiones, podemos
a
Si a = 2, entonces l = 360.
Si a = 3, entonces l = 240.
Finalmente, podemos registrar los valores en una tabla.
Ejercicios y problemas propuestos
1. ¿Cuál de las siguientes situaciones corresponde a
una relación de proporcionalidad inversa?
A. La diferencia de estatura de dos amigos al
ir creciendo.
B. Comer dos frutas al día.
C. Mientras más rápido camino de mi casa al
colegio, menos tiempo me demoro.
D. La cantidad de partes de una torta que se
obtiene al dividirla por la mitad, luego, cada
pedazo por la mitad, y así sucesivamente.
2. Si x varía de manera inversamente proporcional
a y, calcula los valores pedidos, utilizando alguna
estrategia aprendida. Considera que si y es
12 entonces x es 6.
a.
b.
c.
d.
146
Calcula x si y es 5.
Calcula y si x es 3.
Calcula x si y es 15.
Calcula y si x es 1.
Unidad 5 – Álgebra
e.
f.
g.
h.
Calcula x si y es 20.
Calcula y si x es 75.
Calcula x si y es 90.
Calcula y si x es 1 035.
3. Dos variables son inversamente proporcionales si:
A.
B.
C.
D.
su cociente es constante.
su diferencia es constante.
su producto es constante.
su suma es constante.
4. Si x = 7 calcula el valor de y en cada caso.
a. x · y = 8
c. 3y = 49
b. 3x = 4
y
x
d.
81 = 9
xy
5. Calcula mentalmente cada valor, sabiendo que v
es inversamente proporcional a t, y que v es 22
cuando t es 10.
a. Calcula t si v es 11.
b. Calcula v si t es 24.
c. Calcula t si v es 2,2.
d. Calcula v si t es 20.
e. Calcula t si v es 55.
f. Calcula v si t es 110.
6. Dos caballos tardan 3 horas en comer unos fardos
de alfalfa. Si llegara otro caballo y se les diera
de comer la misma cantidad de alfalfa, ¿cuánto
tiempo demorarán los caballos si todos comen
lo mismo? Marca la opción correcta.
A. 1 h
B. 2 h
C. 3 h
D. 4 h
7. Escribe la función que relaciona las variables en
cada caso.
a. Si a varía inversamente respecto de b, y a = 4
cuando b = 5.
b. Si z es inversamente proporcional a x, y x = 12
cuando z = 18.
c. Si y es inversamente proporcional a x, y su
constante de proporcionalidad es 100.
d. Si m y n son inversamente proporcionales y su
constante de proporcionalidad es 36.
8. Completa la tabla sabiendo que las variables x e
y son inversamente proporcionales, y su constante de proporcionalidad es 2 .
3
x
4
8
y
7
32
15
9. Considera que la cantidad de baldosas (b) para
cubrir el piso de un casino depende del tamaño
de las baldosas, es decir, del área (a) que cubre
cada una de ellas.
a. Completa la siguiente tabla:
b
1 600
a (m2)
0,25
0,1
1
10. Un auto de carrera demora 3 horas en recorrer
600 km. Si su velocidad disminuye a la cuarta parte,
¿cuánto demora en recorrer la misma distancia?
Marca la opción correcta.
A. 150 h
B. 200 h
C. 12 h
D. 14 h
11. Se requiere organizar 600 sillas en un salón
de eventos.
a. Si se forman 20 filas con igual cantidad de sillas
cada una, ¿cuántas sillas hay en cada fila?
b. Si las filas tienen 12 sillas cada una, ¿cuántas
filas se pueden formar?
c. Escribe la función que relaciona la cantidad
de sillas por filas y la cantidad de filas.
12. Gabriel, Daniela y Alejandro trabajan cortando el
pasto. Cada uno realiza la misma cantidad de trabajo. Los tres juntos demoran 4 horas en el jardín
de doña Alicia. Si cierto día Alejandro se ausenta,
¿cuánto demoran Daniela y Gabriel en cortar el
pasto del jardín de doña Alicia?
13. Escribe dos ejemplos de variables que se relacionen
de manera:
a. directamente proporcional.
b. inversamente proporcional.
c. no proporcional.
14. Enrique tiene que envasar su producción de jugo
de manzana. Si lo hace en envases de 1 litro
2
necesita 120 envases.
a. ¿Cómo varía la cantidad de envases que
necesitará si varía la capacidad de ellos?
b. Completa la siguiente tabla.
Capacidad del
envase (cm3)
2
b. Escribe una función que relacione las variables
del problema.
c. ¿Cuántas baldosas cuadradas de lado 20 cm
se requieren para cubrir el casino?
d. Si se utiliza un tipo de baldosa que cubre
0,16 m2 y cuyo costo unitario es de $ 300,
¿cuánto habrá que pagar por las baldosas
necesarias para cubrir el casino?
Unidad 5
Patricio Retamal Lizana
Cantidad de
envases
120
250
240
300
c. Calcula el valor de la constante k.
d. Interpreta el significado del valor de la
constante k.
e. ¿Cuántos envases de 100 cm3 necesitará
Enrique para envasar su producción?
f. Si la producción se distribuyó en 50 envases
iguales, ¿cuál es su capacidad?
Unidad 5 – Álgebra
147
Patricio Retamal Lizana
Preparando el SIMCE
Marca la opción correcta en los ítems 1 al 21.
1. En la ecuación x + 3y = 8, ¿cuál es el valor de x
si y = 2?
A. 2
B. 4
C. 5
D. 6
2. Pedro relaciona la cantidad (x) de páginas que lee
de un libro durante una cantidad (y) de minutos,
mediante la expresión x = 3y + 2. ¿Qué tabla
cumple con esta relación?
A.
B.
x
y
0
C.
x
y
2
2
0
1
5
5
1
2
8
8
2
x
y
x
y
8
2
5
1
11
3
8
2
4
4
D.
10
3
3. Juan tiene ahorrado $ 2 500 pesos y cada mes su
madre le regala $ 500. Si m representa la cantidad
de meses que su madre le ha dado dinero y a
representa el dinero que tiene ahorrado Juan,
entonces la ecuación que relaciona m y a es:
A. m = 2 500a
B. m = 500a
C. m = 2 500 + 500a
D. a = 2 500 + 500m
4. La fórmula para calcular la longitud de una
circunferencia está dada por P = 2πr. Si el radio
de la circunferencia es 8 cm, ¿cuál de los siguientes
valores representa su longitud considerando
π = 3?
A. 96 cm
B. 48 cm
C. 24 cm
D. 6 cm
A partir de la siguiente situación responde los ítems
5 al 7.
Para una exhibición de cine hay 3 500 entradas
disponibles y cada una vale $ 2 500.
5. La función que entrega las ganancias ( g) por
número (x) de entradas vendidas es:
A. g (x) = 3 500x
B. g (x) = 2 500x
148
Unidad 5 – Álgebra
C. g (x) = 6 000x
D. g (x) = x
6. El dominio de la función anterior es el conjunto
de los números enteros que están entre:
A. 0 y 2 500
B. 0 y 3 500
C. 0 y 6 000
D. 0 y 1 000
7. El recorrido de la función de las ganancias son
números enteros que están entre:
A. 0 y 2 500
B. 0 y 3 500
C. 0 y 6 000
D. 0 y 8 750 000
8. Considerando que una impresora imprime
12 páginas por minuto, entonces se puede
afirmar que en una hora imprimirá:
A. 600 páginas.
B. 720 páginas.
C. 100 páginas.
D. 120 páginas.
9. En promedio, el corazón de un adulto palpita
8 veces en 6 segundos. La expresión que permite
calcular la cantidad de palpitaciones de un adulto
en m segundos es:
6
8m
A. 8m
6
C.
B. 6m
8
D.
8
6m
A partir de la siguiente situación, responde los
ítems 10 y 11.
Para regular el calor, una estufa dispone de los tres
niveles de consumo de gas que se muestran en
la tabla.
Máximo
Mediano
Mínimo
300 g/h
220 g/h
130 g/h
10. ¿Cuánto tiempo puede estar encendida la estufa
con 500 g de gas en el máximo nivel?
A.
B.
C.
D.
Entre 40 y 50 minutos.
Entre 50 y 70 minutos.
Entre 70 y 90 minutos.
Entre 90 y 110 minutos.
11. ¿Cuántos gramos de gas consume la estufa
encendida en el nivel mínimo durante 8 horas?
A.
B.
C.
D.
Entre 700 y 800 gramos.
Entre 800 y 900 gramos.
Entre 900 y 1 000 gramos.
Entre 1 000 y 1 100 gramos.
12. Fabiola tiene 300 dulces para regalar. ¿Qué función
determina la cantidad (c) de dulces que le quedan
a Fabiola si regala 2 a cada niño (n) que encuentra?
A. c = n – 2
B. c = 300 – n
C. c = 300 – 2n
D. c = 2 + 300n
13. Si la cantidad de arroz que consume una familia al
mes es proporcional al número de sus integrantes,
¿cuánto consume una familia de 5 personas al
mes, si una de 3 personas consume 1,5 kg?
A. 5 kg
B. 4 kg
C. 3,5 kg
D. 2,5 kg
14. El gráfico muestra cómo varían dos magnitudes
x e y. ¿En cuál de los tramos se produce una
variación directamente proporcional entre
las variables?
Unidad 5
Patricio Retamal Lizana
18. Si los lados de un rectángulo aumentan
proporcionalmente en un factor k, ¿en qué
factor aumenta el área del rectángulo?
A. k
B. k
C. 2k
2
D. k
2
19. ¿Cómo se mantiene constante el área de un
triángulo rectángulo si la medida de uno de sus
catetos disminuye un 50 %?
A.
B.
C.
D.
Aumentando el otro cateto en un 50 %.
Aumentando el otro cateto en un 100 %.
Aumentando el otro cateto en un 150 %.
Aumentando el otro cateto en un 200 %.
20. Dos variables son inversamente proporcionales y
su producto es 5. Si una variable toma el valor 8,
la otra toma el valor:
A. 5
8
B. 8
5
C. 40
D. No se puede determinar.
21. Dos variables son directamente proporcionales y
su cociente es 10. Si la primera toma el valor 4, la
segunda toma el valor:
A. 10
C. 40
4
B. 4
D. No se puede determinar.
10
A. Entre 0 y 1.
B. Entre 1 y 2.
C. Entre 2 y 3.
D. Entre 3 y 4.
15. Cinco albañiles construyen una obra en 30 días.
¿Cuánto hubiera demorado la construcción de la
misma obra con dos albañiles menos, al mismo
ritmo de trabajo?
A. 50 días.
B. 12 días.
22. En el siguiente gráfico se muestra la variación de
las medidas de los lados de un rectángulo,
considerando que su área permanece constante.
C. 14 días.
D. 18 días.
16. Con $ p se compran 8 volantines. ¿Qué expresión
permite calcular la cantidad de volantines que se
pueden comprar con $ r?
A. r · 8
p
p
B.
·8
r
C. r
8
D. p
8
17. ¿Qué nombre recibe la gráfica que se relaciona
con una proporcionalidad inversa?
A. Parábola.
B. Hipérbola.
C. Recta.
D. Catenaria.
a. Si el largo del rectángulo es 12 cm, ¿cuál es la
medida de su ancho?
b. ¿Qué tipo de proporcionalidad se da entre
estas variables?
c. Calcula la constante de proporcionalidad y
explica su significado en la situación.
Unidad 5 – Álgebra
149
Patricio Retamal Lizana
Evaluación de síntesis de la unidad 5
Marca la opción correcta en los ítems 1 al 13.
1. Se relaciona el perímetro de un triángulo equilátero
con la medida de uno de sus lados, mediante
la ecuación P = 3a, donde P es el perímetro del
triángulo y a la medida del lado. ¿Cuánto mide el
lado del triángulo si su perímetro es 54 cm?
A. 18 m
B. 162 m
C. 18 cm
D. 162 cm
A. 3 días.
B. 6 días.
C. {5, 9, 11, 17}
D. {7, 9, 11, 13}
4. Fabián es 5 años mayor que su hermano José. Si
denotamos por f la edad de Fabián y por j la de
José, la relación de las edades de los hermanos se
puede escribir como:
C. f = j + 5
D. j = f + 5
5. ¿Cuál de las siguientes relaciones, cuyo dominio es
el conjunto de los números naturales, corresponde
a una función?
A. A cada número del dominio se le asocian dos
números mayores que él.
B. A cada número del dominio se le asocian
todos los números menores que él.
C. A cada número del dominio se le asocian su
antecesor y sucesor.
D. A cada número del dominio se le asocia
su sucesor.
6. La tabla muestra una relación entre dos variables.
¿De qué tipo es?
A.
B.
C.
D.
150
Directamente proporcional.
Inversamente proporcional.
No proporcional.
Decrecimiento exponencial.
Unidad 5 – Álgebra
C. 18 manzanas.
D. 19 manzanas.
9. Una bandeja de huevos dura 20 días si comen
3 personas diariamente la misma cantidad cada
uno. ¿Cuántos días dura la bandeja si comen
6 personas la misma cantidad de huevos?
3. Si el dominio de la función g(x) = 2x – 1
es {3, 5, 6, 9}, su recorrido es:
A. 5f = j
B. f = 5j
20 cm de ancho y 70 cm de largo.
60 cm de ancho y 160 cm de largo.
15 cm de ancho y 40 cm de largo.
6 cm de largo y 16 cm de ancho.
A. 16 manzanas.
B. 17 manzanas.
La variable dependiente es x.
La variable independiente es y.
y está en función de x.
f es la variable independiente.
A. {1, 3, 5, 7}
B. {3, 5, 7, 9}
A.
B.
C.
D.
8. Mauricio come dos manzanas cada día. ¿Cuántas
manzanas come en 9 días?
2. En la función y = f (x) = 4x + 1, la afirmación
correcta es:
A.
B.
C.
D.
7. Felipe mandó a imprimir un dibujo de 30 cm de
ancho y 80 cm de largo. ¿Cuál de las siguientes
medidas corresponde a una reducción proporcional del dibujo?
r
s
2
1
4
2
8
4
C. 10 días.
D. 15 días.
10. Una fábrica produce juguetes en serie. Si cada
4 horas elabora 7 juguetes, ¿cuántos juguetes
puede producir en 12 horas?
A.
B.
C.
D.
28 juguetes.
21 juguetes.
Aproximadamente 20 juguetes.
14 juguetes.
11. En la pregunta anterior, si llamamos h a las horas
y j a los juguetes, la ecuación que modela la
situación es:
A. h = 7 j
4
B. 28 = j · h
C. 4h = 7j
D. 4j = 7h
12. La expresión x · y = 3 indica que:
A.
B.
C.
D.
x e y no son proporcionales.
x es directamente proporcional a y.
y es directamente proporcional a x.
x e y son inversamente proporcionales.
13. ¿Qué tipo de relación muestra el gráfico?
A. Directamente
proporcional.
B. Inversamente
proporcional.
C. No proporcional.
D. De crecimiento
exponencial.
14. Completa las siguientes igualdades considerando
los valores de la tabla:
a.
b.
c.
d.
f (3) =
f( ) = 9
f (21) =
f( ) = 6
f (s)
3
4
p
10
5
b
8
6
a
10
9
q
4
0,2
1
15. A partir de la pregunta anterior, determina:
a. El dominio de la función f (s).
b. El recorrido de la función f (s).
1
2
3
Término (t)
22
24
26
4
5
a. ¿Por qué esta relación es una función?
b. Determina la variable independiente y la
variable dependiente.
c. Completa la tabla.
d. Encuentra los números de las posiciones 15,
25 y x, considerando que f (n) = 20 + 2n.
17. ¿Cuál es el dominio de la función f (x) = 5x + 1,
sabiendo que su recorrido es el conjunto
{1, 11, 21, 31}?
18. Determina para cada caso si la afirmación es
verdadera o falsa. Justifica las falsas.
a.
El tiempo que me demoro en digitar
un trabajo es inversamente proporcional a la
cantidad de páginas que se requiere digitar.
b.
El monto de la cuenta de luz es inversamente proporcional a la cantidad de energía
que se consume.
c.
El tiempo que demora un bus en hacer
su recorrido es inversamente proporcional a la
cantidad de pasajeros que transporta.
d.
20. Determina en cada caso si las variables son
inversamente proporcionales, directamente
proporcionales o si no son proporcionales.
a. 16. Considera la siguiente secuencia: 22, 24, 26, 28,
30, 32… La tabla muestra la relación entre un
término de la secuencia y el lugar que ocupa.
Ubicación en la
secuencia (n)
19. En la siguiente tabla, los valores de p y q son
inversamente proporcionales. ¿Cuál es el valor
de a + b?
s
21
La distancia que recorre un auto, a una
velocidad constante, es directamente proporcional al tiempo que se demora en recorrerla.
Unidad 5
Patricio Retamal Lizana
x
y
2
c.
x
y
4
2
3
4
16
4
5
6
36
6
7
8
64
8
9
b. x
y
x
y
2
18
2
12
4
16
4
6
6
14
6
4
8
12
8
3
d.
21. Escribe, en cada caso, la ecuación que representa
la relación entre las variables. Da un ejemplo
donde podrías ocupar esta función.
a. Si a varía inversamente con b, y a = 7 cuando
b = 49.
b. Si z es directamente proporcional a x, y z = 14
cuando x = 16.
c. Si x varía inversamente con z, y x = 181 cuando
z = 9.
22. Considera que x e y son magnitudes directamente
proporcionales y responde.
a. Respecto de la tabla de valores siguiente, ¿cuál
es la constante de proporcionalidad?
x
2
6
18
y
4
12
36
b. Ahora, respecto de la siguiente tabla de valores,
¿cuáles son los valores de r y q?
x
20
45
q
y
r
7
2
Unidad 5 – Álgebra
151