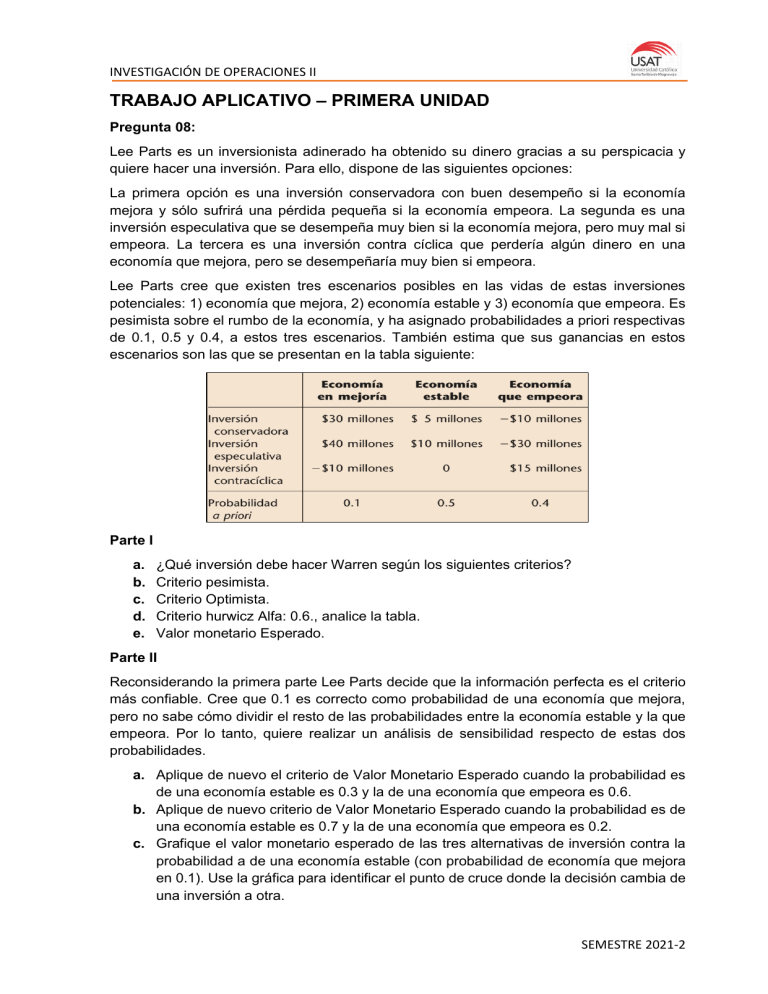
INVESTIGACIÓN DE OPERACIONES II TRABAJO APLICATIVO – PRIMERA UNIDAD Pregunta 08: Lee Parts es un inversionista adinerado ha obtenido su dinero gracias a su perspicacia y quiere hacer una inversión. Para ello, dispone de las siguientes opciones: La primera opción es una inversión conservadora con buen desempeño si la economía mejora y sólo sufrirá una pérdida pequeña si la economía empeora. La segunda es una inversión especulativa que se desempeña muy bien si la economía mejora, pero muy mal si empeora. La tercera es una inversión contra cíclica que perdería algún dinero en una economía que mejora, pero se desempeñaría muy bien si empeora. Lee Parts cree que existen tres escenarios posibles en las vidas de estas inversiones potenciales: 1) economía que mejora, 2) economía estable y 3) economía que empeora. Es pesimista sobre el rumbo de la economía, y ha asignado probabilidades a priori respectivas de 0.1, 0.5 y 0.4, a estos tres escenarios. También estima que sus ganancias en estos escenarios son las que se presentan en la tabla siguiente: Parte I a. b. c. d. e. ¿Qué inversión debe hacer Warren según los siguientes criterios? Criterio pesimista. Criterio Optimista. Criterio hurwicz Alfa: 0.6., analice la tabla. Valor monetario Esperado. Parte II Reconsiderando la primera parte Lee Parts decide que la información perfecta es el criterio más confiable. Cree que 0.1 es correcto como probabilidad de una economía que mejora, pero no sabe cómo dividir el resto de las probabilidades entre la economía estable y la que empeora. Por lo tanto, quiere realizar un análisis de sensibilidad respecto de estas dos probabilidades. a. Aplique de nuevo el criterio de Valor Monetario Esperado cuando la probabilidad es de una economía estable es 0.3 y la de una economía que empeora es 0.6. b. Aplique de nuevo criterio de Valor Monetario Esperado cuando la probabilidad es de una economía estable es 0.7 y la de una economía que empeora es 0.2. c. Grafique el valor monetario esperado de las tres alternativas de inversión contra la probabilidad a de una economía estable (con probabilidad de economía que mejora en 0.1). Use la gráfica para identificar el punto de cruce donde la decisión cambia de una inversión a otra. SEMESTRE 2021-2 INVESTIGACIÓN DE OPERACIONES II Pregunta 08: La federación peruana de deportes realiza pruebas antidoping de sus deportistas, 15% de los cuales usan drogas. Esta prueba tiene sólo 97% de confiabilidad. Es decir, un atleta que usa drogas saldrá positivo con probabilidad 0.97 y negativo con probabilidad 0.03, y aquel que no consume estupefacientes saldrá negativo y positivo con probabilidades respectivas de 0.97 y 0.03. a. Desarrolle un árbol para determinar la probabilidad a posteriori de los resultados de someter a prueba a un atleta. b. Es usuario de drogas, dado que la prueba es positiva. c. No es usuario, dado que la prueba es positiva. d. Es usuario de drogas dado que la prueba es negativa. e. No es usuario, dado que la prueba es negativa. Pregunta 09: La administración de la compañía el Leoncito Feroz estudia el desarrollo y comercialización de un nuevo producto. Se estima que hay el doble de posibilidades de que el producto tenga éxito a que no lo tenga. Si tiene éxito, la ganancia esperada sería $1 500 000. Si no es así, la pérdida esperada sería $1 800 000. Se puede hacer una investigación de mercado a un costo de 300 000 dólares para predecir si tendrá o no éxito. La experiencia indica que se ha pronosticado éxito de productos exitosos 80% del tiempo y fracaso de productos no exitosos 70% del tiempo. a. Desarrolle una formulación para el análisis de decisión de este problema mediante la identificación de las opciones alternativas, los estados de la naturaleza y la matriz de pagos cuando se realiza el estudio de mercado. b. Suponga que no se realiza el estudio de mercado; use el criterio del valor monetario esperado para determinar qué alternativa debe elegirse. c. Encuentre el VEIP. ¿Indica esta respuesta que debe tomarse en cuenta la realización del estudio de mercado? d. Suponga que se realiza el estudio de mercado. Encuentre las probabilidades a posteriori de los respectivos estados de las dos predicciones posibles del estudio de mercado. e. Encuentre la política óptima para determinar si se debe realizar el estudio y si se debe desarrollar y vender el nuevo producto. Pregunta 10: La Empresa ABC tiene 100 millones de dólares sobrantes de fondos para inversión. Ha recibido instrucciones de invertir la cantidad completa a un año en acciones o en bonos (pero no en ambos) y después reinvertir el fondo completo ya sea en acciones o bonos (pero no en ambos) un año más. El objetivo es maximizar el valor monetario esperado del fondo al final de segundo año. Las tasas de interés anual sobre estas inversiones dependen de la situación económica, como se muestra en la siguiente tabla: SEMESTRE 2021-2 INVESTIGACIÓN DE OPERACIONES II Las respectivas probabilidades de crecimiento, recesión y depresión del primer año son 0.7, 0.3 y 0. Si ocurre el crecimiento en el primer año, estas probabilidades son las mismas para el segundo año, pero, si ocurre una recesión el primer año, las probabilidades cambian a 0.2, 0.7 y 0.1 para el segundo. a. Construya a mano el árbol de decisión del problema. b. Analice el árbol para identificar la política óptima. Pregunta 11: La empresa SAM S.A produce lotes de aparatos con 0.8%, 1%, 1.2% y 1.4% de aparatos defectuosos de acuerdo con las probabilidades respectivas, 0.4, 0.3, 0.25 y 0.05. Tres clientes, A, B, y C están contratados para recibir lotes con no más de 0.8%, 1.2% y 1.4% de aparatos defectuosos, respectivamente. Si los aparatos defectuosos resultan ser más que los contratados, se penaliza a SAM S.A con $100 por cada 0.1% de incremento. Si SAM S.A surte lotes con mayor calidad que la requerida le cuesta $50 por cada 0.1% por debajo de las especificaciones. Suponga que no se inspeccionan los lotes antes de su envío. a. Desarrolle el árbol de decisiones asociado. b. ¿Cuál de los tres clientes debe tener la más alta prioridad para recibir su pedido? Pregunta 12: Great Apps of Ann Arbor, LLC by Robert M. Freund Great-Apps-of-Ann-Arbor, LLC (“Great-Apps”), formerly named Graphic Corporation, is an internet start-up in Ann Arbor, Michigan that develops smartphone apps for local businesses. Kate Harmon conceived of and then started the firm while in business school. She is now President and CEO of its new incarnation in a large light-industrial-use property the firm owns on the outskirts of Ann Arbor at 297 Huron River Drive. The 297 Huron building space is outfitted for the sales force, software teams, customer support, and ancillary general management. The decision to purchase the warehouse was not taken lightly: it is a significant capital investment in the future of the business. It is now May and the coming summer weather is likely to provide a routine seasonal drop in new business. But Kate’s concern is not with her sales but rather with the roof of 297 Huron Drive. Last winter’s record snowfall weakened the flat roofs of many warehouses in the area. According to the Detroit Free Press, ten years ago in a similarly heavy winter, 8% of all warehouses of similar size and design needed to have their roofs replaced. The problem is that one cannot know whether the roof needs replacing or not without opening up the roof, xraying the beam welds, and conducting beam stress tests, all of which is prohibitively expensive. SEMESTRE 2021-2 INVESTIGACIÓN DE OPERACIONES II As a result of last winter’s snowfall, many industrial property owners in the area have already contracted to replace their roofs this coming summer. (Summer is the ideal time to do roof replacement work for a variety of reasons including better weather and less disruption of ordinary business operations.) Kate Harmon had recently asked Steve Lauprete, who manages general operations at Great-Apps, to look into the roof replacement matter further. Steve determined that they should replace the roof within the next 16 months (essentially by the end of the next summer). However, he recommended waiting until the start of next summer (13 months from now) to do the replacement, since the very high demand for contractors this summer had pushed the bids up an average of $150,000 beyond the ordinary costs of roof replacement contracts. If they postpone the planned roof replacement until the next summer and the roof nevertheless needs replacement in the coming winter, it would probably show signs of imminent failure with the first large snowfall of the winter. In that case the extra cost (beyond the ordinary cost of summer roof replacement) of replacing the roof in the winter would then be $360,000, due to more extensive operations work-arounds and weather-related construction delays. Steve Lauprete also looked into the possibility of pre-testing the integrity of the roof. Nemirovski Analytics does non-invasive steel beam and weld testing using wave imaging methods. They charge $20,000 to conduct such tests. Because their tests are not invasive, the results are imperfect. The output of the test is a rating of “Positive,” “Negative,” or “Inconclusive.” If the roof needs to be replaced this summer, then the chance that it would test Negative is 75%, and the chance that it would test Inconclusive is 10%. (This implies that the chance that it would test Positive is 15% in this case.) If the roof replacement can wait until next summer, then the chance that it would test Positive is 70%, and the chance that it would test Inconclusive is 20%. (This implies that the chance that it would test Negative is 10% in this case.) Kate Harmon thought things over. She sure would rather think about developing apps for customers than replacing roofs. She knew several large firms were watching Great-Apps and one never knew when an offer might materialize to purchase Great-Apps. She wouldn’t want a winter roof replacement to appear to others as a sign of poor management. She thought that the potential distraction and embarrassment cost of replacing the roof in the winter would be on the order of $100,000. Assignment: If you were Kate Harmon, what decision strategy would you pursue? SEMESTRE 2021-2