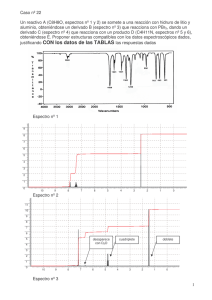
4 Espectroscopia de transmisión en películas delgadas A Una película delgada es de manera resumida, una lámina muy delgada (orden de magnitud 1 micra) de espesor muy homogéneo y de extensión algunos centímetros, usualmente los materiales involucrados son semiconductores, dieléctricos, polímeros, etc., básicamente materiales para dispositivos electrónicos Debido al hecho de ser delgados es complicado medir sus espesores mecánicamente, por lo que el método óptico resulta lo más apropiado, por ser muy preciso, rápido y no altera la muestra. OBJETIVO Estimar el espesor de una película delgada usando su espectro de transmisión INTRODUCCION Cuando la luz se refleja en una capa delgada de aceite que flota en agua o en una burbuja de jabón, es común ver bandas brillantes de colores (como se muestra en la Figura 1). . Figura 1: Pompa de Jabón con los reflejos multicolores típicos Los colores no son del material, así por ejemplo la burbuja esta formada básicamente por agua transparente. Los colores se producen por efecto de la configuración de la burbuja al reflejo de la luz Éstos son los resultados de la interferencia. Las ondas luminosas se reflejan en las superficies anterior y posterior de esas finas películas y se produce interferencia constructiva entre las dos ondas reflejadas (cada color corresponde a un espesor definido) que cumple en este caso con la condición de máxima reflexión. Fundamento Espectroscopia (Rango visible) La Espectroscopia es la rama de la rama de la ciencia que permite analizar e identificar las luces (o radiación en general) proveniente de cualquier fuente. El principio de funcionamiento de un espectrómetro (originalmente óptico) es la disposición de un elemento dispersor, por ejemplo un prisma. Desde tiempos remotos era conocido el efecto de un prisma en descomponer (dispersar) la luz blanca del sol en los colores típicos del arco iris (figura 2 ), Newton fue quien con su tratado de óptica le dio mayor difusión, no obstante para una explicación explicita del efecto se tuvo que esperar 100 años mas tarde con el advenimiento de las teorías ondulatorias. Figura 2: Efecto de dispersión de un prisma a la incidencia de un haz de luz blanca Figura 3 : Diagrama esquemático de la composición del espectrómetro básico: El monocromador En la figura 3 se muestra la configuración del espectrómetro mas elemental y común: El monocromador, el que esta constituido por: Una fuente de luz blanca, una rendija de entrada (Slit) una rendija de salida (Ss), un detector fotoeléctrico (D) y un sistema de rotación prismático, que escanea las longitudes de onda de salida. Figura 4: Se muestra de manera esquemática la configuración de un monocromador básico en base a una rejilla de difracción como elemento dispersivo. En la figura 4 se muestra otro modelo de monocromador más moderno, en el que en vez de un prisma se emplea una rejilla de difracción reflectiva, que de igual modo que el prisma permite dispersar la luz, mayormente con mucha mejor resolución. Espectros Básicos Esencialmente al realizar un análisis de las luces mas comunes con que tratamos ordinariamente, encontramos 2 tipos: Espectros continuos Generados esencialmente por calor, como por ejemplo las lámparas incandescentes o la misma radiación solar. En la figura 5 se presenta un espectro continuo clásico: de una lámpara incandescente (lámpara halógena) Figura 5 : Espectro continuo (por ejemplo, de una lámpara incandescente) Figura 6: Espectros discreto (p. e. lámparas de descarga): H, Na, Mg Espectros Discretos Generados esencialmente por descargas fluorescentes o las lámparas de neón). eléctricas (por ejemplo En la figura 6 se muestra algunas líneas espectrales oscuras montadas sobre un espectro continuo, esta descripción corresponde esencialmente a espectros de absorción selectiva de los elementos indicados, no obstante los espectros de líneas de emision (espectros discretos) provenientes de los distintos elementos son patrones luminosos exclusivos en un fondo oscuro, como se muestra en la figura 7 para algunos elementos comunes. Figura 7: Espectros de líneas que se presentan para algunos elementos. El gran potencial de la espectroscopia se dio cuando los astrónomos empezaron a analizar las luces de las estrellas, descubriendo que contienen los mismos materiales comunes que en la tierra. Antes de estos trabajos era inconcebible saber algo de los astros sin haber llegado a ellos. Mediciones de Transmitancia Las medidas de espectros de transmisión son esencialmente comparativas, en primer lugar se mide con el espectrómetro a disposición un espectro continuo básico y en segundo lugar, sin cambiar las condiciones de seteo (p.e. ancho de las rendijas, intensidad de la lámpara, distancias) se vuelve a tomar otro espectro, pero con la muestra insertada en el camino óptico (de modo transversal) (ver figura 8). Luego se realiza la comparación espectral del resultado obtenido con la muestra a la obtenida sin la muestra y se obtiene así el espectro de transmisión. En nuestro caso las mediciones de espectros de transmitancia en esta práctica se efectúan mediante un espectrómetro (Photonic Multi Chanel Analyser) HAMAMATSU C7473, por el cual se obtiene directamente en el ordenador el espectro de emisión respectivo y el operador debe trabajar con los datos medidos para obtener el espectro de transmisión resultante Figura 8: Diagrama esquemático que describe el procedimiento de medición de la señal de transmisión de una muestra en forma de película delgada. Fundamento Teórico: El Espectro de Transmisión Al incidir un haz de luz monocromático λ de manera normal sobre una película de espesor d y de índice de refracción n, la fracción de radiación transmitida T, está dada por la relación T = t122 t212 / (1+ r214 – 2 r212 cos 2kd) Dónde: t12 = (2n / 1 + n) t21 = (2 / 1 + n) r12 = (1 – n / 1 + n) r21 = (n - 1 / 1+ n) k = 2πn/λ Por tanto, si la radiación monocromática que incide sobre la muestra varia en cierto rango espectral, el coeficiente de transmisión T, asumirá valores máximos o mínimos de acuerdo a que se cumplan las siguientes condiciones: Máximos: 2kd = 2 N π O correspondientemente 2nd = N λ Mínimos: 2kd = 2 (N + ½) π O correspondientemente 2nd = (N + ½) λ Por tanto el espectro resultante será de tipo acanalado (con máximos y mínimos sucesivos), bastando encontrar un solo valor N (orden de la interferencia) para poder deducir el espesor d de la muestra y de igual modo, si fuera el caso se puede establecer la dependencia espectral del índice de refracción n del material. Caso Introductorio: El etalon Fabry Perot Figura 9: Configuración esquemática de un etalon Fabry Perot: 2 vidrios sumamente planos con recubrimientos metálicos altamente reflejantes se montan uno frente al otro, tal que se forma una zona plano paralela de espesor d. El etalon Fabry Perot es un dispositivo óptico interferometrico que se emplea entre otros fines a filtrar rayos de luz. Se construye en base a 2 láminas de vidrio muy planas, las que han sido recubiertas con una pequeña capita de algún material reflejante (por ejemplo aluminio). Las 2 superficies reflejante se montan una frente a la otra, como se muestra en la figura 9, El rayo incidente I, por reflexiones multiples entre los 2 semiespejos va a producir tanto en reflexión como en transmisión un gran numero de reflexiones y transmisiones parciales (en el grafico solo se muestran 3: t1,t2,t3), todas las cuales contribuyen a realizar un coeficiente total T, cuya ecuación particular para incidencia normal al etalon se indicó previamente. Si se hace pasar por el etalon un pulso infrarojo (cerca de 1.54 μm de longitud de onda) de ancho espectral aproximado de 40 nm, el pulso transmitido va a presentar los máximos y mínimos típicos de las reflexiones múltiples (figura 10). Para analizar este resultado, basta escoger 2 máximos relativos (sucesivos); del espectro resultante hemos escogido 2 (ver figura 10): λ1 = 1547.7 nm y λ2 = 1543.7 nm Al máximo correspondiente a λ1 le asignamos el orden N y al máximo siguiente le corresponde el orden N + 1. Ya que entre los 2 espejos plano paralelos solo hay aire, entonces el índice de refracción n = 1. Figura 10: Espectro resultante del paso de un pulso infrarojo por un etalon Fabry Perot. A partir de estos datos encuentre Ud. el espesor de la interface de aire que forma el Fabry Perot y el orden N correspondiente al máximo en λ1. (ojo: ¡N debe ser un numero entero!)