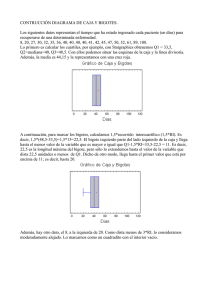
UNIVERSIDAD JUÁREZ AUTÓNOMA DE TABASCO MAESTRÍA EN CIENCIAS AGROALIMENTARIAS Métodos estadísticos Tema: Medidas de dispersión 1.- Con los datos siguientes construya el gráfico de caja y bigotes. En ambos ejemplos interprete los que significan los siguientes valores: mediana, rango del bigotesuperior, y rango interquartil. 1)Peso en kilogramos de 12 alumnos de la asignatura de genética: 45, 60, 65, 52, 50, 54, 71, 64, 58, 66, 47, 74 5 X 45 47 50 52 54 58 60 64 65 66 71 74 Fi 1 1 1 1 1 1 1 1 1 1 1 1 10 15 Fa 1 2 3 4 5 6 7 8 9 10 11 12 20 25 Q1 = Kn/4 Q1= 1*12= 12/4 Q1= 3 Limite interior= Q1-1.5*RIQ 50-1.5*15=50-22.5=27.5, Quiere decir que los valores que están por debajo de 27.5 son Atípicos. Q2= 2*12= 24/4 Q2= 6 Límite superior= Q3+1.5*RIQ 65+1.5*15= 65+22.5= 87.5, Los valores que están por encima de 87.5 son atípicos. Q3= 3*12=36/4 Q3= 9 Rango Intercuartílico RIQ RIQ= Q3-Q1 RIQ= 50-65= 15, Este valor representa lo ancho que tendrá la caja. 30 35 40 45 50 LI 55 60 65 70 75 Q2 Q1 DM- 80 85 90 LS Q3 Rango Intercuartil DM El límite inferior es 27.5, esto indica que los valores menores son atípicos, en este grafico el dato menor es 45, por lo que no hay valores atípicos en este sector. La caja inicia en el Q1 que es 50, Q2 es la mediana y Q3 equivale al 75%. La caja es el rango intercuartílico que corresponde a Q1-Q3 y el bigote 1 que se forma inicia del limite inferior 27.5 al Q1, el segundo bigote comienza en el Q3 hasta el límite superior que es 87, siendo el dato menor 74, lo que nos indica que en este sector no hay valores atípicos, por lo que se puede deducir que los alumnos de la asignatura de genética se encuentran dentro de su peso adecuado. 2) Horas promedio de internet que consumen 20 hogares 4, 7, 8, 9, 7, 6, 5, 10, 11, 12, 5, 3, 8, 12, 13, 10, 6, 4, 7, 9 X Fi 3 4 5 6 7 8 9 10 11 12 13 1 Fa 1 2 2 2 3 2 2 2 1 2 1 2 1 3 5 7 10 12 14 16 17 19 20 N= 20 3 4 5 Q1 DM Q1 = Kn/4 Q1= 1*20= 20/4 Q1= 5 Limite interior= Q1-1.5*RIQ 5-1.5*5=5-7.5=2.5, Quiere decir que los valores que están por debajo de 2.5 son Atípicos. Q2= 2*20= 40/4 Q2= 10 Límite superior= Q3+1.5*RIQ 10+1.5*5= 10+7.5= 17.5, Los valores que están por encima de 17.5 son atípicos. Q3= 3*20=60/4 Q3= 15 Rango Intercuartílico RIQ RIQ= Q3-Q1 RIQ= 10-5= 5, Este valor representa lo ancho que tendrá la caja. 6 7 Q2 8 9 10 11 12 13 14 15 16 17 18 19 Q3 DM La caja inicia en el Q1 que corresponde a 5, Q2 es la mediana que es 7, y Q3 equivale a 10, que corresponden a 25, 50 y 75% respectivamente. La caja es el rango intercuartílico que abarca el Q1-Q3 y el primer bigote inicia del límite inferior 3 al Q1, el segundo bigote comienza en el Q3 hasta el límite superior que es 13, siendo el dato menor. 2.- A partir de los siguientes conjuntos de datos determine el coeficiente de asimetría y de curtosis 1) Número de trabajadores con licencia media durante 10 días 10, 12, 9, 7, 12, 15, 14, 16, 11, 13 X 7 9 10 11 12 12 13 14 15 16 N=10 119 x 11.9 11.9 11.9 11.9 11.9 11.9 11.9 11.9 11.9 11.9 (X-x) -4.9 -2.9 -1.9 -0.9 0.1 0.1 1.1 2.1 3.1 4.1 (X-x)2 24.01 8.41 3.61 0.81 0.01 0.01 1.21 4.41 9.61 16.81 68.9 (Xi-µ)^4 576.5 70.73 13.03 0.66 0.0001 0.0001 1.47 19.45 92.35 282.58 1,056.7702 Ϭ= √ 68.9 = √6.89= 2.625 10 Me= 12 Cap= 3 (11.9-12) = 0. 1143 2.625 µ= 11.9 Ϭ= 2.625 g2 = 1,056.7702/10*(2.625)^4 = 22.26 2) Datos de la tasa de incrementos de precios al consumo (%), en 2010, para 24 países seleccionados de la OCDE: 2.2, 7.6, 2.9, 4.6, 4.1, 3.9, 7.4, 3.2, 5.1, 5.3, 20.1, 2.3, 5.5, 32.7, 9.1, 1.7, 3.2, 5.8, 16.3, 15.9, 5.9, 6.7, 3.4, 40.5 X 1.7 2.2 2.3 2.9 3.2 3.2 3.4 3.9 4.1 4.6 5.1 5.3 5.5 5.8 5.9 6.7 7.4 7.6 9.1 15.9 16.3 20.1 32.7 40.5 N=24 215.4 x 8.975 8.975 8.975 8.975 8.975 8.975 8.975 8.975 8.975 8.975 8.975 8.975 8.975 8.975 8.975 8.975 8.975 8.975 8.975 8.975 8.975 8.975 8.975 8.975 (X-x) (X-x)2 (Xi-µ)^4 -7.275 52.925625 2801.12178 -6.775 45.900625 2106.86738 -6.675 44.555625 1985.20372 -6.075 36.905625 1362.02516 -5.775 33.350625 1112.26419 -5.775 33.350625 1112.26419 -5.575 31.080625 966.00525 -5.075 25.755625 663.352219 -4.875 23.765625 564.804932 -4.375 19.140625 366.363525 -3.875 15.015625 225.468994 -3.675 13.505625 182.401907 -3.475 12.075625 145.820719 -3.175 10.080625 101.619 -3.075 9.455625 89.4088441 -2.275 5.175625 26.7870941 -1.575 2.480625 6.15350039 -1.375 1.890625 3.57446289 0.125 0.015625 0.00024414 6.925 47.955625 2299.74197 7.325 53.655625 2878.92609 11.125 123.765625 15317.9299 23.725 562.875625 316828.969 31.525 993.825625 987689.373 0 2198.505 1338836.45 Ϭ= √ 2198.505 = √91.6044 = 9.6 24 Me= 5.4 Cap= 3 (8.975-24) = 4.7 9.6 µ= 8.975 Ϭ= 9.6 g2 = 1338836.45/24*(9.6)^4 = 157.7 3.- En la siguiente tabla se presenta la frecuencia de vuelos retrasados y el intervalo de tiempo del retraso en un aeropuerto. Para los datos calcule las medidas de dispersión. Duración del retraso (centésimas de hora) 0-10 10-20 20-30 30-50 50-100 Marca de clase Xi 5 15 25 40 75 Media 32 Número de vuelos 2000 3000 2500 2000 500 Frecuencia fi 2000 3000 2500 2000 500 N= 10,000 X por F Xi2 *f (Xi) (Xi-µ)^4 10,000 45,000 62,500 80,000 37,500 235,000 50000 675000 1562500 3200000 2812500 8,300.000 531441 83521 2401 4096 3418801 Desv. media 20.4 Cap= 3 (32-10,000) = 1,465.9 20.4 g2 = 10,000(4,040,260/5*(20.4)^4 = 23,342.11 4,040,260