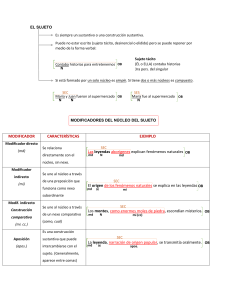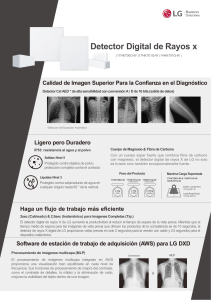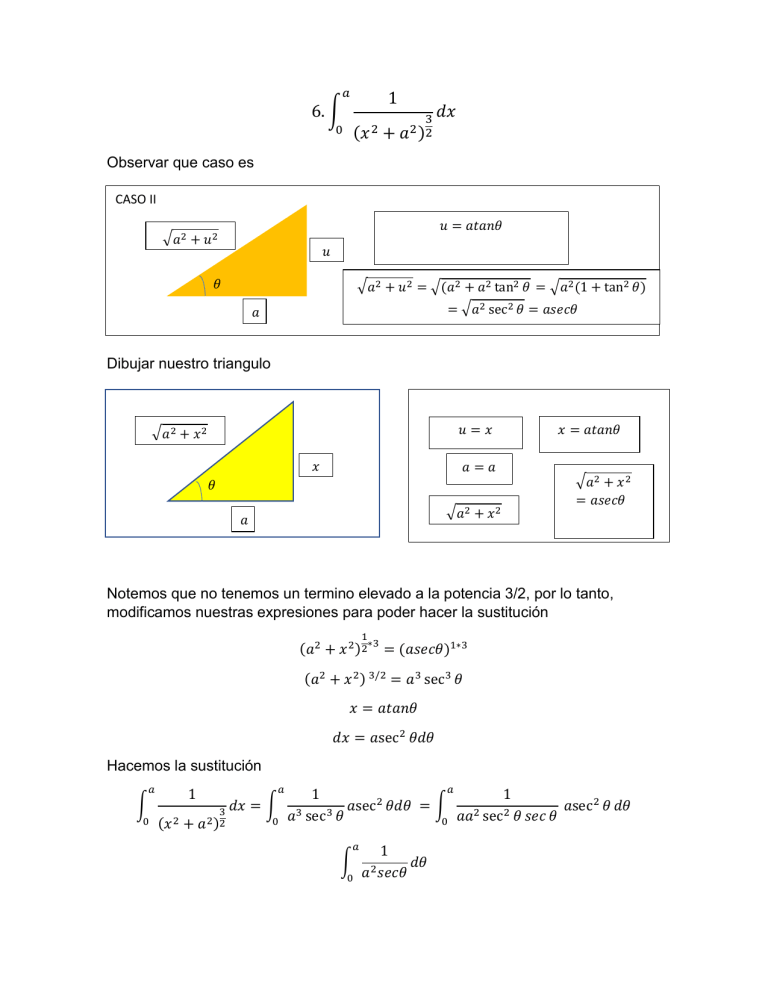
𝑎 1 6. ∫ (𝑥 2 0 + 3 𝑑𝑥 2 𝑎 )2 Observar que caso es CASO II 𝑢 = 𝑎𝑡𝑎𝑛𝜃 √𝑎2 + 𝑢2 𝑢 𝜃 √𝑎2 + 𝑢2 = √(𝑎2 + 𝑎2 tan2 𝜃 = √𝑎2 (1 + tan2 𝜃) = √𝑎2 sec 2 𝜃 = 𝑎𝑠𝑒𝑐𝜃 𝑎 Dibujar nuestro triangulo 𝑢=𝑥 √𝑎2 + 𝑥 2 𝑥 𝑥 = 𝑎𝑡𝑎𝑛𝜃 𝑎=𝑎 𝜃 √𝑎2 + 𝑥 2 𝑎 √𝑎2 + 𝑥 2 = 𝑎𝑠𝑒𝑐𝜃 Notemos que no tenemos un termino elevado a la potencia 3/2, por lo tanto, modificamos nuestras expresiones para poder hacer la sustitución 1 (𝑎2 + 𝑥 2 )2∗3 = (𝑎𝑠𝑒𝑐𝜃)1∗3 (𝑎2 + 𝑥 2 ) 3/2 = 𝑎3 sec 3 𝜃 𝑥 = 𝑎𝑡𝑎𝑛𝜃 𝑑𝑥 = 𝑎sec 2 𝜃𝑑𝜃 Hacemos la sustitución 𝑎 ∫ 0 1 𝑎 3 𝑑𝑥 = ∫ (𝑥 2 + 𝑎2 )2 0 𝑎 1 1 2 𝑎sec 𝜃𝑑𝜃 = ∫ 𝑎sec 2 𝜃 𝑑𝜃 3 3 2 2 𝜃 𝑠𝑒𝑐 𝜃 𝑎 sec 𝜃 𝑎𝑎 sec 0 𝑎 ∫ 0 1 𝑎2 𝑠𝑒𝑐𝜃 𝑑𝜃 Sacamos la constante 1 𝑎 1 ∫ 𝑑𝜃 𝑎2 0 𝑠𝑒𝑐𝜃 Usamos una expresión trigonométrica que relaciona a la secante y al coseno 1 𝑎 ∫ 𝑐𝑜𝑠𝜃𝑑𝜃 𝑎2 0 Resolvemos la integral 1 𝑎 𝑠𝑒𝑛𝜃 | 2 𝑎 0 Sustituimos el ángulo usando nuestro triangulo 1 𝑥 𝑎 | 𝑎2 √𝑎2 + 𝑥 2 0 Evaluamos en los límites de integración, todo donde este una x pondremos una a 1 𝑎 2 𝑎 √𝑎2 + 𝑎2 Reducimos 1 𝑎√2𝑎2 1 𝑎√2𝑎 1 √2𝑎2