interes simple y compuesto

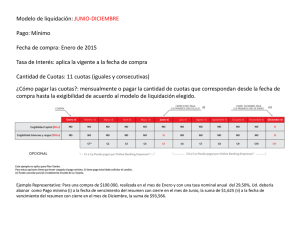
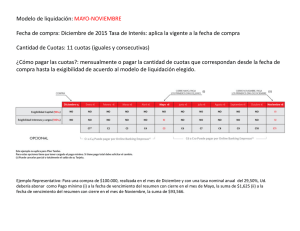
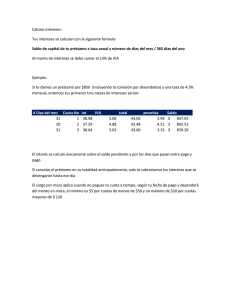
GUIA DE APRENDIZAJE Nº2 PORCENTAJE
INTERÉS SIMPLE Y COMPUESTO
¿Qué es el interés?
Antes de entrar en detalle veamos qué es el interés. Es un índice por medio del cual se mide
la rentabilidad de los ahorros y las inversiones. También sirve para medir el costo de un crédito
bancario. Este costo se representa como un porcentaje referido con el total de la inversión o el
crédito. En este sentido cabe destacar que al momento de contratar un producto bancario que
genere rentabilidad buscamos que la tasa de interés sea la más alta ya que es un interés que
nos pagará el banco, mientras que cuando solicitamos un crédito buscamos que la tasa de
interés sea baja ya que es un interés que pagaremos al banco.
Interés Simple: ¿Qué es?
Se considera que la tasa de interés es
simple cuando el interés que se obtiene al
vencimiento no se suma al capital para
poder generar nuevos intereses. Este tipo de
interés se calcula siempre sobre nuestro
capital inicial. Por esta razón, los intereses
que vamos obteniendo no se reinvierten en
el siguiente período, debido a esto el interés
obtenido en cada período es el mismo.
Interés Simple: Fórmula
Podemos obtener el interés simple que produce
un capital con la siguiente fórmula:
Is = Ci * i * n
Ejemplo: Si queremos calcular el interés simple
que produce un capital de 1.000.000 pesos
invertido durante 5 años a una tasa del 8%
anual. El interés simple se calculará de la
siguiente forma:
Interés Simple: Características
Is = $ 1.000.000 * 0,08 * 5
Is = $ 400.000
Las
principales
características
del
Interés Simple son:
A)
El capital inicial se mantiene igual Si queremos calcular el mismo interés durante un
periodo menor a un año (60 días), se calculará
durante toda la operación.
de la siguiente forma:
B)
El interés es el mismo para cada uno Período: 60 días = 60/360 = 0,16
de los períodos de la operación.
C)
La tasa de interés se aplica sobre el
capital invertido o capital inicial.
Calculando el interés simple
Determinemos el interés simple, si se
deposita $100 a una tasa de interés de 14%
durante tres años.
Is = $ 1.000.000 * 0,08 * 60/360 Is
= $ 13.333
Is = Ci * i * n
Is = $100 x 0,14 x 3
Is = $ 42
El interés acumulado es $42. El total en la cuenta
será $142.
Interés Compuesto: ¿Qué es?
En este tipo de interés, los intereses que se
consiguen en cada periodo se van sumando
al capital inicial, con lo que se generan
nuevos intereses. En este tipo de interés a
diferencia del interés simple, los intereses
no se pagan a su vencimiento, porque se
van acumulando al capital. Por esta razón,
el capital crece al final de cada uno de los
periodos y el interés calculado sobre un
capital mayor también crece. Es lo que se
conoce como "interés sobre interés", y
así como puede ser muy atractivo en los
productos
que
generan
rentabilidad,
también es muy perjudicial en los créditos
ya
que
la
deuda
aumenta
exponencialmente.
Interés Compuesto: Fórmula
Podemos obtener el interés compuesto que
produce un capital con la siguiente fórmula:
Cf = Ci * (1 + i)
n
Ejemplo sencillo de interés compuesto:
Grace quiere ahorrar una cantidad inicial de
$1.000.000 a un interés compuesto mensual de
5% por 3 meses. ¿Cuánto recibirá Grace al final
de los tres meses? Lo primero que haremos será
identificar los datos:
Ci = $ 1.000.000
i = 5% (0,05) n
=3
Interés Compuesto: Características Las
principales características del Interés
Cf = Ci * (1 + i) n
Compuesto son:
Cf = $ 1.000.000 * (1 + 0,05)3
A)
El capital inicial aumenta en cada
Cf = $ 1.157.625
periodo debido a que los intereses se van
sumando.
IC = Cf – Ci
Por lo tanto el interés compuesto del período fue
B)
La tasa de interés se aplica sobre un
de $ 157.625
capital que va variando.
C)
Los intereses son cada vez mayores.
Calculando el interés compuesto
Si se comienza con un depósito de $500 y
una tasa de interés compuesto del 6%
anual. ¿Cuánto dinero se tendría después de
5 años?
Cf
= Ci (1 + i)
Cf
= 500 * (1 + 0,06)5
Cf
= 500 * (1,06)5
n
Cf = $ 669,11.
IC = Cf – Ci
Por lo tanto el interés compuesto del período fue
de $ 169,11
Comparación entre interés simple y compuesto.
Supongamos que vamos a colocar durante 5 años un capital de $1.000 en dos bancos, el primero
en interés simple y el segundo en interés compuesto, del 10% anual en ambos casos.
En el primer banco, cada año, el capital inicial produciría un interés de 1.000 · 10% = 100. Así,
al acabar el primer año tendríamos $1.100. Al final del segundo año (al no acumularse el interés)
tendríamos $1.200 y al final del tercero $1.300, del cuarto $1.400 y del quinto $1.500.
En el segundo banco el primer año obtendríamos un interés de 1.000 · 10%=100 y al acabar el
primer año tendríamos $1.100. Para calcular el interés en el segundo año (al acumularse los
intereses) tendríamos 1.100 · 10% = 110, y al final del segundo año tendríamos $1.210. Al final
del tercer año tendríamos $1.331, al final del cuarto $1.464,10 y al final del quinto $1.610,51
Como puede observarse en el ejemplo, el interés compuesto produce un mayor capital final que
el interés simple para un mismo capital durante el mismo tiempo. A un año los capitales finales
que producen son iguales. Por este motivo suele utilizarse el interés compuesto en operaciones
de duración superior a un año y el interés simple en operaciones de duración inferior al año.
EJEMPLOS
1. Si solicito $500.000 a un prestamista con en 24 cuotas mensuales con un interés simple de
1 % mensual, ¿Cuánto terminare pagando por el préstamo?
Solución: La ganancia para el prestamista será igual a
G = Is = C i * i * n
donde
n = 24 porque son 24 períodos de 1 mes en donde se aplicará el interés,
i = 1 % = 1 /100 y
Ci = $500.000
G = 24 · 1/ 100 · 500.000 = $120.000
El prestamista gana $120.000, por lo tanto terminare pagando las ganancias G del
prestamista más el dinero prestado C, esto es:
C + G = $500.000 + $120.000 = $620.000
2. Si ahorro $1.000 en una cuenta de ahorro con interés simple de un 12 % anual, ¿cuánto
tendré en la cuenta 24 meses después?
Solución:
Para este caso el capital es Ci =$1.000,
El interés i = 12 % = 12/ 100 = 3/ 25 anual. Los 24 meses los transformamos a 2 años
para que n y el interés i estén con la misma temporalidad.
Transcurridos los 2 años tendré en mi cuenta el capital inicial C más las ganancias G por
interés.
Ahorro = C + G = $1.000 + C*i*n
= $1.000 + $2 · 3 /25 · 1.000
= $1.000 + $240 = $1.240
3. ¿Cuál es el ahorro obtenido al depositar $1.000.000 en una cuenta con una tasa de interés
del 10 % anual durante 48 meses?
Solución: En este caso Ci = $1.000.000, i = 10 % = 0, 1 anual y n = 48 meses.
Como i y n deben estar en la misma temporalidad, reescribimos n = 48 / 12 = 4 años.
Sabemos que: Cf = Ci(1 + i)
n
Nos preguntan por Cf, entonces:
Cf = Ci (1 + i) 4
= 1.000.000(1 + 0, 1)4
= 1.000.000(1, 1)4 = $1.464.100
4.- El precio en efectivo de un notebook es de $750.000. Si al comprarlo en 6 cuotas se le
aplica un interés compuesto mensual de 6 %, ¿cuál es la diferencia monetaria entre
pagarlo en 6 cuotas y en efectivo?
Solución: El costo final en 6 cuotas lo podemos hallar con la expresión: C6 = Ci(1 + i)
donde i = 6 % = 0, 06
Ci =$750.000,
6
entonces el precio final a pagar por el notebook es:
Cf = Ci(1 + i) 6
=750.000 (1 + 0, 06)6
= 750.000(1, 06)6 = $1.063.890
La diferencia entre el precio en cuotas y en efectivo es:
$1.063.890 − $750.000 = $313.890
Si calculamos qué porcentaje es $313.890 de $750.000 obtenemos un 41,85 %, eso quiere
decir que al comprarlo en 6 cuotas estamos pagando un %41,85 extra del precio en
efectivo.
EJERCICIOS DE INTERÉS SIMPLE, COMPUESTO Y PORCENTAJE
1.- María le quiere comprar un teléfono a su amiga Marta. El precio al contado es
de 96.000 pesos. María ha pagado una cuota inicial de 12.000 , y el saldo lo pagará después
de 6 meses. Su amiga le acepta este pago tardío, pero con una tasa de
interés de 18% anual. ¿Cuánto pagará María al final por la compra del teléfono?
2.- Tiana pide un préstamo de 2. 400.000 pesos a una tasa de interés simple de 10% anual
para pagarlo en 3 años. ¿Cuál es el monto total que pagará Tiana al término de los 3 años?
3.- Alexander pide un préstamo de 1.000.000 a su amigo Pedro, quien accede a prestar el
dinero con la condición de que al término de 6 meses Alexander devuelva el monto final
considerando una tasa de interés simple. Si al término de este plazo, Alexander pagó 1.
135.000 pesos, ¿cuál es la tasa de interés simple que le aplicó Pedro al préstamo?
4.- Si un capital prestado al 2.5% mensual durante año y medio ha producido un interés
de 32.400 dólares, ¿cuál es el valor de dicho capital?
5.- Un capital de 100 000 $ se coloca al 6,5 % anual durante 6 meses, 1 año o 5 años.
Calcula el capital final producido en los diferentes periodos de tiempo tanto a interés
simple o compuesto y determina cuál de ellos es beneficioso según el tiempo.
6.- Ingreso 1.500.000 $ en un banco y se comprometen a pagarme un 3,7 % anual,
abonando los intereses semestralmente. ¿Cuánto dinero tengo al cabo de 4 años?
7.- Un banco que opera por internet ofrece su cuenta azul a un 5,5 % anual de interés
que se paga mensualmente. Si abro una cuenta con 4.000.000 $ y acumulo en esa cuenta
los intereses mensuales que me pagan, ¿cuánto dinero tendré al cabo de 3 años?
Respuestas:
1.- 103.560
2.- 3.120.000
3.- 27%
4.- 72.000
5.- 6 meses: 1.032.500 1.031.900
1 año: 1.065.000
5 años: 1.325.000 1.370.100
6.- 1.736.850
7.-4.715.600