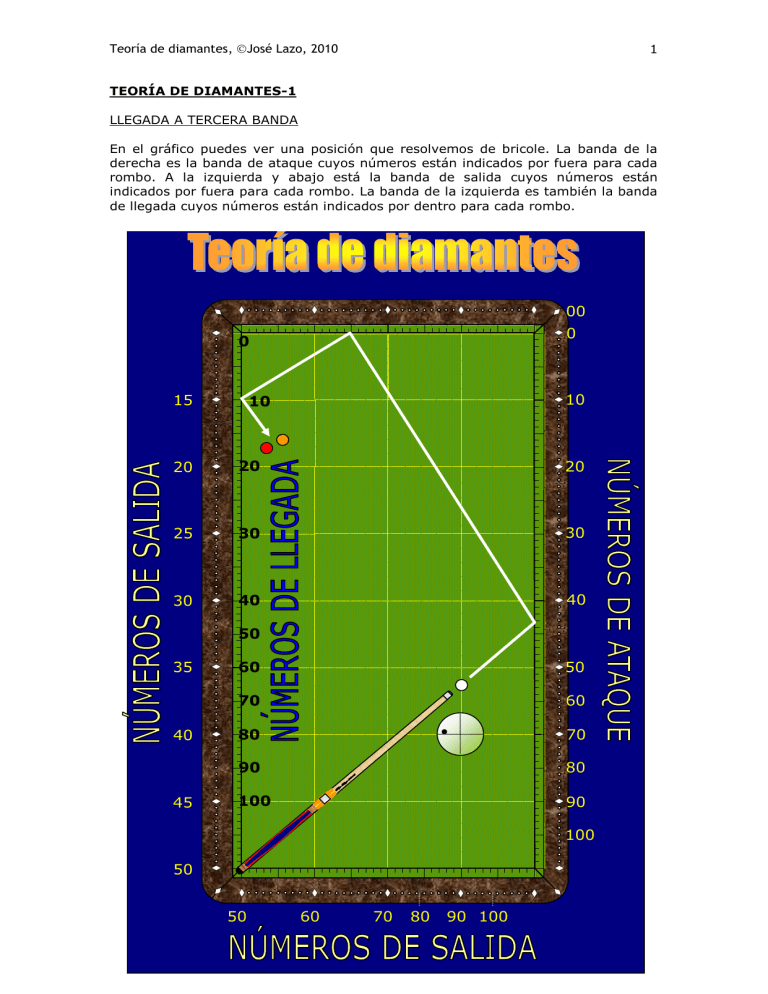
Teoría de diamantes, José Lazo, 2010 1 TEORÍA DE DIAMANTES-1 LLEGADA A TERCERA BANDA En el gráfico puedes ver una posición que resolvemos de bricole. La banda de la derecha es la banda de ataque cuyos números están indicados por fuera para cada rombo. A la izquierda y abajo está la banda de salida cuyos números están indicados por fuera para cada rombo. La banda de la izquierda es también la banda de llegada cuyos números están indicados por dentro para cada rombo. 00 0 0 15 10 10 20 20 20 25 30 30 30 40 40 50 35 40 45 60 50 70 60 80 70 90 80 100 90 100 50 50 60 70 80 90 100 Teoría de diamantes, José Lazo, 2010 2 La fórmula para deducir el punto de ataque es: SALIDA – LLEGADA = ATAQUE Y al respecto hago tres observaciones: 1ª) Para determinadas posiciones hay que realizar alguna corrección que ya veremos más adelante. 2ª) Personalmente el sistema de direcciones que aplico es el siguiente: PUNTO DE ATAQUE: hacia el rombo 00 0 0 15 10 10 20 20 20 25 30 30 PUNTO DE ATAQUE 30 40 40 50 35 40 45 60 50 70 60 80 70 90 80 100 90 100 50 50 60 70 80 90 100 Teoría de diamantes, José Lazo, 2010 3 PUNTO DE LLEGADA: en el vértice de la banda. 00 0 0 PUNTO DE LLEGADA 15 10 10 20 20 20 25 30 30 30 40 40 50 35 40 45 60 50 70 60 80 70 90 80 100 90 100 50 50 60 70 80 90 100 Teoría de diamantes, José Lazo, 2010 4 PUNTO DE SALIDA: en el vértice de la banda 00 0 0 15 10 10 20 20 20 25 30 30 30 40 40 50 35 40 45 60 50 70 60 80 70 90 80 100 90 100 50 50 60 70 80 90 100 PUNTO DE SALIDA Muchos jugadores toman como punto de salida el lugar por donde asa el taco a la altura del rombo y no por el vértice de la banda. En el caso concreto que he puesto ellos no considerarían ese lugar de salida como 50 sino más o menos 47,5, aunque personalmente me resulta algo extraño pues lo hacen al considerar que según los números de salida de la banda corta inferior es aproximadamente ese valor, pero si tenemos en cuenta los números de salida de la banda larga izquierda será 52,5. Es difícil de entender como estando la bola en un sitio pudiera tener dos números Teoría de diamantes, José Lazo, 2010 5 posibles de salida según se tome como criterio la banda corta o la banda larga. Pongo otro ejemplo para que se vea más claro: 00 0 0 15 10 10 20 20 20 25 30 30 30 40 40 50 35 40 Según mi método la salida es 60 al pasar mi taco por ese valor en el vértice 45 60 50 70 60 80 70 90 80 100 90 100 50 50 60 70 80 Otros utilizan como valor 60 de salida por donde pasa el taco a la altura del rombo 90 100 Teoría de diamantes, José Lazo, 2010 6 Sin embargo a todos nos funciona más o menos el sistema. Esto es debido a la diferencia de golpeo de un jugador a otro. Un pequeño matiz en el efecto, la penetración o incluso la velocidad alteran los resultados. Por tanto cada uno con su golpe puede buscar la fórmula que le aporte los resultados esperados. Esto será siempre una constante en el juego del billar. 3ª) Un error que si creo que puede ser frecuente es la forma de realizar los cálculos. Muchos jugadores comienzan a pensar así: "como salgo de la salida 63 y quiero alcanzar la llegada 25, me da el punto de ataque 63-25 = 38" y, sin embargo, cuando se colocan se dan cuenta de que no están realmente en la salida 63. Esto es especialmente frecuente cuando la bola jugadora no está cerca de la banda de salida. Observa el gráfico. 20 30 30 40 60 63 38 Teoría de diamantes, José Lazo, 2010 7 Si mantiene el ataque a ese lugar presumiblemente va a fallar la posición. También tiene la alternativa de realizar algún pequeño ajuste hasta dar con la diferencia adecuada. Yo recomiendo más bien el siguiente sistema: 1º) Deducir la llegada: en este caso es 25 2º) Buscar líneas SALIDA-ATAQUE que den ese valor. En el ejemplo que he puesto anteriormente y de una manera intuitiva consideramos que la bola jugadora está en la zona de salida aproximadamente 60 o 65. Las diferencias de estos valores con la llegada son respectivamente 35 (60-25) y 40 (65-25), pues bien, con el taco extendido visualizamos ambas líneas. 20 30 30 35 40 60 65 Teoría de diamantes, José Lazo, 2010 8 Observamos que la bola jugadora está prácticamente en la línea 65-40 (ligeramente desplazada hacia la izquierda), así que una paralela muy próxima nos indica que deberíamos atacar a muy poco menos del rombo 40. "A la oreja izquierda del rombo" como solía decir mi maestro Alejandro Muñoz. Veamos otro ejemplo: 5 10 40 45 50 Teoría de diamantes, José Lazo, 2010 9 La llegada es 40. La bola jugadora está en la zona de salida entre 50 y 45, las diferencias con la llegada son respectivamente 10 y 5. La bola jugadora está aproximadamente en el centro de esas dos líneas, así que trazamos una paralela a ambas y nos aporta el punto de ataque. Una última consideración básica es cuando la bola jugadora está cerca de la banda de ataque, hay que tener cuidado pues al golpear y llegar rápidamente a la banda de ataque es normal que se produzca un cuadraje y se cierren los ángulos. La forma de corregirlo es o bien atacamos ligeramente más adelante (lo que se antoja como algo más bien intuitivo y muy delicado) o no imprimir demasiada velocidad (golpe más moderado) para evitar la deformación excesiva de la banda. PROLONGACIÓN HACIA CUARTA, QUINTA Y SEXTA BANDA Una proporción importantísima de soluciones de tres bandas son de cuatro, cinco o más bandas. La teoría de diamantes es tan amplia que nos permite definir unas líneas maestras de llegada desde la tercera banda hasta la cuarta, desde la cuarta hasta la quinta, desde la quinta hasta la sexta, etc. Esto viene a significar que muchas soluciones de carambolas dan el mismo resultado en el cálculo siempre y cuando la llega sea la misma e independientemente del número de bandas con la que se quiere lograr. Resulta evidente que no es lo mismo tres bandas que seis o siete especialmente en lo que se refiere a velocidad de la bola jugadora. Si además pretendemos entrenar técnicas de preparación donde ponemos como condición llegar a la bola 3 y separarla unos 15-30 cm, deducimos que la velocidad para tres bandas es menor que para cinco o seis por ejemplo. Las consecuencias de la velocidad ya se han indicado en algún artículo anterior, no obstante, es importante recordarlas. Una velocidad moderada supone una disminución rápida de la misma por rozamiento no solo en su desplazamiento sino en el giro de la bola jugadora como consecuencia de haber dado efecto. Es decir, la calidad del efecto se perderá antes. Si en cambio imprimimos una velocidad alta, las consecuencias del rozamiento tanto en la velocidad como en el giro por el efecto de la bola jugadora aparecerán más tarde, en otras palabras, se mantendrá la calidad más tiempo. Lo anterior nos lleva a la conclusión de que no debemos imprimir la misma velocidad si queremos resolver una posición solo a tres bandas o a seis bandas por ejemplo aunque las líneas maestras indiquen que las llegadas sean las mismas. Insisto que es importante llegar a la zona de caramboleo con la bola 3 y separarla unos 15-30 cm, por tanto es un ejercicio que se debería practicar con cierta frecuencia. Colocar posiciones, por ejemplo de bricole y procurar llegar a la zona de caramboleo con esas condición anterior. Hay métodos de corrección según los cuales si pretendemos por ejemplo una solución a cinco o seis bandas se ataca un poco más adelante para compensar posibles cuadrajes y siempre imprimiendo más o menos la misma velocidad a la jugadora. Estos métodos están incluso tabulados pero requieren tener bastante retentiva memorística. La educación en cambio de las distintas velocidades no requiere prácticamente ningún ajuste en la fórmula y, por tanto, ninguna desviación en el punto de ataque. Teoría de diamantes, José Lazo, 2010 10 Las prolongaciones de tercera banda a cuarta son las siguientes: 00 0 0 10 15 10 20 20 20 30 25 30 40 30 40 35 40 45 50 50 60 60 70 70 80 80 90 90 100 100 50 50 60 70 80 90 100 Observa como las líneas de llegada se van acercando a partir especialmente de 40 a 100. Esto va a tener una influencia importante en la decisión de por donde resolver una determinada posición (marcha de juego). Teoría de diamantes, José Lazo, 2010 11 Las prolongaciones de cuarta a quinta y de quinta a sexta son las siguientes: 00 0 0 10 15 10 20 20 20 30 25 30 40 30 40 35 40 45 50 50 60 60 70 70 80 80 90 90 100 100 50 50 60 70 80 90 100 Como puedes ver prácticamente ya es todo una continuidad de líneas paralelas con llegadas desde 50 a 100 muy próximas y llegadas desde 0 hasta 50 más separadas. De hecho las llegadas 10, 20 o 30 son relativamente delicadas, mientras que llegadas superiores a 50 hacen "más gorda" la solución. ¿Te has fijado que una bola a cinco o seis bandas suele ser más fácil que una de tres o cuatro?. Pues algo tiene que ver esta proximidad de líneas. Teoría de diamantes, José Lazo, 2010 12 Y ya para acabar este primer capítulo entenderás que todas estas posiciones se resuelven con el mismo punto de ataque: 30 30 60