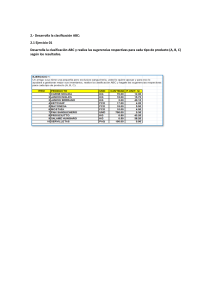
87 CAPITULO III INDUCCIÓN - DEDUCCIÓN En relación con el estudio de la matemática en nuestra sociedad, encontramos aún algunos prejuicios: unos dicen, por ejemplo, sólo personas de gran talento, pueden dedicarse a la matemática, mientras que otros afirman que para ello es preciso tener una "memoria matemática" capaz de permitir recordar fórmulas y saber cómo y cuándo aplicarlas. Las expresiones: "soy incapaz para la matemática", "no he nacido para los números", "me falta memoria para aprender todas las fórmulas", etc., etc., son un producto amargo del tipo de enseñanza memorística y mecanizada que hemos recibido desde nuestra infancia, debido a la falta de un sistema educativo adecuado, objetivo y verdaderamente científico capaz de satisfacer las expectativas de la gran mayoría de estudiantes y no sólo de un sector, cuyo beneficio obedece claramente a intereses egoístas. En consecuencia, nos corresponde revertir esta situación, poniendo en práctica nuestra capacidad de raciocinio y análisis objetivo. Contribuiremos a ello, en esta parte del curso, desarrollando la parte inductivadeductiva de nuestro razonamiento para lograr, de esta manera, un mayor grado de abstracción. Quizá en algunas ocasiones, durante la búsqueda de la solución de alguna interrogante relacionada con nuestra vida diaria o al intentar resolver problemas netamente matemáticos, nos hayamos encontrado un tanto desorientados sobre cómo afrontarlos, entonces nos asaltó la duda y surgieron las eternas preguntas: ¿Por dónde empezar? ¿Qué estrategia plantear y seguir? Parte de culpa de estar en dicha situación la tiene el hecho de no tener en claro los conceptos de razonamiento, pensamiento creativo, lógica deductiva, lógica inductiva, etc. El objetivo entonces del presente capítulo será estudiar los diversos conceptos y aplicarlos manejando criterios adecuados, desarrollando, además, ejemplos necesarios para un mejor desenvolvimiento dentro del curso de razonamiento y actividades en general. Nunca olvides que el primer paso es comprender el problema, una vez logrado esto debes dar el siguiente paso: idear cómo afrontarlo; cada problema debe ser un reto, para ello debes leer atentamente la parte teórica y rescatar las mayores observaciones de cada ejemplo. Después de haber resuelto un problema, debes valorar más el proceso inductivo-deductivo y no tanto la respuesta, ello te permitirá salir airoso en cada problema siguiente. 88 ¿Qué es estrategia? Analiza atentamente las siguientes situaciones: ? Alejandro Carlos Calcular la suma de las cifras de A A = (33 .... 33)² 100 cifras En la primera de ellas una pelota ha caído por un estrecho orificio, no tan profundo, pero no al alcance de los brazos de Alejandro; él no dispone de palos ni varas para extraerla; Juan, que estaba sacando agua, observa la escena y se pregunta: ¿qué hará él para poder sacar la pelota? En el siguiente caso Carlos está frente a un problema que se ve muy laborioso: ¿cómo resolverlo? En ambos casos será necesario pensar detenidamente sobre la situación y elaborar un plan que les permita conseguir sus objetivos; dicho plan recibe el nombre de estrategia. La palabra estrategia proviene del griego "strategia" (generalato, aptitudes de general), que en el contexto de nuestro interés se entiende como el plan o técnica para dirigir un asunto o para conseguir un objetivo. En la primera situación, una posibilidad sería buscar ayuda, traer herramientas y "ampliar el hueco lo cual no está mal, pero sería muy trabajoso y mostraría que no pensamos mucho sobre el asunto y estamos procediendo de manera mecánica. Otra posibilidad podría ser echar abundante agua por el orificio, la pelota flotará y podremos sacarla, lo cual sería una solución más razonada, ¿no crees? Para resolver la segunda situación, deberemos aplicar la inducción y para ello hay que tener una idea de lo que es razonamiento inductivo-deductivo, nociones que estudiaremos más adelante. ¿Qué es inducción? La palabra inducción proviene del latín "Inductio", ("in" : en y ducere : conducir); que es la acción y efecto de inducir. Es definido como un modo de razonar que consiste en sacar de los hechos particulares una conclusión general; así, la inducción desempeña una gran papel en las ciencias experimentales. Más adelante podremos apreciar la forma de aplicar este modo de razonar en la resolución de problemas matemáticos. ¿Qué es deducción? La deducción es la acción de deducir, también es la conclusión que se obtiene de un proceso deductivo. La palabra deducir, proviene del latín "deducere" que significa sacar consecuencias. En el presente estudio veremos cómo partir de casos generales llegamos a establecer cuestiones particulares que nos interesan para la resolución de problemas. 89 Podemos decir, figurativamente, que la inducción y la deducción son como las dos caras de una misma moneda, estableciéndose como herramientas poderosas que han permitido el avance de la ciencia en general. ¿Cómo hizo Arquímedes para determinar, según él, el valor aproximado del número p y el cálculo de áreas de regiones sumamente complicados para su época? ¿Cómo llegó Kepler a establecer sus tres famosas leyes? 1 ¿De qué manera Galileo procedió para establecer la relación: e = gt²? 2 ¿Sospechas, cómo llegó Newton a dar la ley de la gravitación universal a partir de hechos comunes contemplados por todos nosotros, pero que él supo observar atentamente para enunciar tan importante teoría? y ¿Lobatcheysky, para crear su geometría no euclideana? y ¿Einstein, con su Teoría de la relatividad?... En fin, gran parte de lo establecido hasta ahora por la ciencia se ha hecho en base a la experimentación, a la aplicación de la inducción, y deducción, y al proceso de ensayo-error con el estudio y el análisis de todas las consecuencias que se derivan de ellos, los cuales ha permitido el avance de la ciencia en todos los campos. ¿Cuántos palitos de fósforo conforman el siguiente castillo? ¿Cómo resuelvo este problema? 1 2 29 30 Al igual que Daniela, muchos estudiantes al empezar la resolución de un problema siempre se preguntan: "¿Cómo resuelvo este problema?, ¿por dónde empiezo la resolución del problema?, ¿será este el camino adecuado para su resolución?; indudablemente que para el ejemplo anterior, el contar uno por uno los palitos de fósforos del castillo no sería una resolución adecuada, ya que sería muy tedioso y agotador realizar dicha operación. Siempre que se busca la solución a un problema, debemos buscar los caminos más cortos para llegar a ella, debemos analizar nuestros datos e incógnitas y al relacionarlos debemos encontrar una "estrategia" de cómo afrontar el problema, "ser creativos y analistas" para buscar esa relación de datos con incógnitas. Justamente, a partir de estas ideas ("tener estrategia", "ser creativo y analista"), surgen dos herramientas importantes que nos permiten afrontar un problema: la lógica inductiva y la lógica deductiva. Las lógicas inductiva y deductiva representan la base del razonamiento matemático, pilares sobre los cuales se construye esta hermosa disciplina, en base a la observación y el análisis. 90 Es un modo de razonar, en el que a partir de la observación de casos particulares, nos conducen al descubrimiento de leyes generales, con la particularidad de que la validez de las últimas se deduce de la validez de las primeras. Así: Casos Particulares Razonamiento Inductivo El método del razonamiento inductivo es un método especial de demostración matemática que permite, en base a observaciones particulares, juzgar las regularidades generales correspondientes. Ejemplo: (15)² = 225 (35)² = 1225 (85)² = 7225 Casos particulares (125)² = 15625 Razonamiento Inductivo "Podemos concluir que todo número que termina en 5, al elevarlo al cuadrado, su resultado termina en 25" (....5)² = ......25 Conclusión general Ejemplo 1 Calcular el número total de palitos de fósforo que conforman la torre de la derecha. 1 2 .... .... . Como se observa, contar los palitos uno por uno va a resultar una tarea bastante tediosa. Nos damos cuenta que la distribución de palitos en la torre obedece a una cierta formación (va aumentando uniformemente por pisos), entonces aplicamos inducción, analizando los 3 casos más simples que se puedan encontrar. ...... .......... . .... Resolución: 3................28 29 30 91 Nº de palitos Caso Caso : 2 3 1 2 8 : -1 -1 1 2 Caso 2 15 : -1 ........ ........ En el problema : ........ ........ 1 2 3 .... .... . ...... . .... 2 .......... 1 2 3................28 29 \ Nº de palitos = 899 Ejemplo 2 Calcular el valor de "E" y dar como respuesta la suma de sus cifras. E = (333...334)² 101 cifras - 1 = 899 92 Resolución: Elevar el número al cuadrado resulta muy operativo y tedioso, pero nos damos cuenta también que la base tiene cierta formación (la cifra 3 se repite constantemente); entonces recurrimos a la inducción, analizando los casos simples, análogos al de la expresión "E". (34)² = 1156 Suma de cifras = 13 Þ 6(2) + 1 = 111556 Suma de cifras = 19 Þ 6(3) + 1 = 11115556 Suma de cifras = 25 Þ 6(4) + 1 2 cifras (334)² 3 cifras (3334)² 4 cifras . . . . . . . . . E = (333 … 3334)² = 111 … 1155 … 556 101 cifras 101 cifras Suma de cifras . . . = 6(101) + 1 = 607 101 cifras \ Suma de cifras = 607 Ejemplo 3 Calcular el valor de E= 97 • 98 • 99 • 100 + 1 Resolución: Multiplicar, sumar y extraer la raíz cuadrada va a ser demasiado operativo. Observando detenidamente el problema nos damos cuenta que tiene una particularidad (producto de cuatro números consecutivos); entonces aplicamos inducción, analizando los casos más simples sin que se pierda la forma original del problema. 93 Ejemplo 4 ¿Cuántos apretones de manos se producirán al saludarse las 40 personas asistentes a una reunión? Resolución: Dado que la cantidad de apretones depende del número de personas, vamos a realizar un análisis inductivo de casos particulares, así: # Personas 2 3 4 5 .. . n # de Apretones 1 x 2 2 x 3= 2 6= 3 x 2 4 x 10 = 2. .. .. . 1= 2 3 4 5 2 6 12 20 . .. .. =1x2 =2x3 =3x4 = 4 x. 5 (n - 1)n 2 Caso general para "n" personas \ para 40 personas Þ Respuesta: 39 x 40 2 = 780 apretones. Ejemplo 5 Calcular: E = (1111 … 111 + 222 … 222 + 333 … 333)² 50 cifras Resolución: Por inducción: (1 + 2 + 3)² = 6² = 36 (11 + 22 + 33)² = 66² = 4356 (111 + 222 + 333)² = 666² = 443556 E = 444 … 4443555 … 5556 49 cifras 49 cifras 50 cifras 50 cifras .. .. 94 CURIOSIDADES SOBRE INDUCCIÓN 1² = 1 11² = 121 111² = 12321 1111² = 1234321 11111² = 123454321 111111² = 12345654321 1111111² = 1234567654321 11111111² = 123456787654321 111111111² = 12345678987654321 Observando el resultado en el desarrollo de cada potencia vemos que, iniciando en la cifra1, se ordenan de manera ascendente los números naturales consecutivos, hasta llegar a una cifra que coincida con la cantidad de cifras 1 de la expresión exponencial, para luego descender. 95 LÓGICA DEDUCTIVA (deducción) Es un modo de razonar mediante el cual, a partir de informaciones, casos o criterios generales, se obtiene una conclusión particular. Así : CASO 1 C A S O G E N E R A L CASO 2 CASO 3 Casos Particulares CASO 4 .. .. .. Razonamiento Deductivo Ejemplo: - Todos los hijos de la señora Ana son valientes - Pedro es hijo de la señora Ana Por lo tanto: Pedro es valiente Información general Razonamiento deductivo Conclusión particular Ejemplo 1 La suma de los "n" primeros números impares es 900, por lo tanto, ¿cuál es el valor de "n"? Resolución: Para resolver este problema, primero hay que conocer a qué es igual la suma de los "n" primeros números impares (caso general), para luego verificar el valor de "n" cuando la suma sea 900 (caso particular). 96 1 + 3 = 4 = (2)² 2 términos # de términos 1 + 3 + 5 = 9 = (3)² 3 términos # de términos 1 + 3 + 5 + 7 = 16 = (4)² # de términos 4 términos . . . . Conclusión general : Caso particular : n² = 900 ................ (Dato) \ n = 30 Ejemplo 2 Completar las cifras que faltan en la siguiente multiplicación, sabiendo que cada (asterisco (*) representa un dígito. Resolución: * 3 * 3 * 2 * 2 * 5 1 * 8 * 1 * * 2 3 * * 3 0 Tengamos presente los criterios generales en la multiplicación para aplicarlo en este caso en particular. 4 x 3 = 12 _ 3 _ 3_2 1 2_5 1_ 8_ 1 _ _ 2 3 0 0 3 0 4 3 _ 3_2 1 2_5 1_ 8_ 1 5 _ 2 3 0 0 5 x 3 = ..5 3 0 Finalmente, resolviendo las operaciones: 4 3 8 332 1 245 15 85 1 5 x 8 2 3 0 0 3 0 4 3 _ 33 _2 1 2_5 1_ 8_ 1 5 8 _ 2 3 0 0 3 0 415 x 8 3320 (x) 97 Ejemplo 3 Calcular m, n y p; sabiendo que: m ¹ n ¹ p y además: mmm + nnn + ppp = 2664 Resolución: Ordenando los números en columna: Llevamos de la 1ª columna Llevamos de la 2ª columna 1ra. Columna : m + n + p = ........ 4 3ra. Columna : m + n + p + 2 = 26 De la 1ra. y la 3ra. Columna, se deduce que: m + n + p = 2 4 2 2 mmm + n n n p p p 2664 Buscando tres dígitos diferentes cuya suma sea igual a 24, encontramos: m = 7 ; n = 8 ; p = 9 \ Respuesta : 7 x 8 x 9 = 504 Ejemplo 4 Hallar : E = abcd + mnpp + xyzw, sabiendo que: bd + np + yw = 160 ac + mp + xz = 127 ab + mn + xy = 124 Resolución: Considerando los criterios generales de la adición, ordenamos cada uno de los datos, así: i) bd + np yw 160 De i) y iii) se deduce: ii) 1ro. iii) ac + mp xz 127 ab + mn xy 124 d + p + w = 20 2do. b + n + y = 14 En iii): como : b + n + y = 14, entonces : a + m + x = 11 En ii): como : a + m + x = 11, entonces : c + p + z = 17 Luego, hallando E: E = abcd + mnpp + xyzw \ E = 12590 112 . abcd + mnpp x yzw 12590 98 EJERCICIO 1 Si a la siguiente figura le trazamos 50 rectas paralelas a MN, ¿cuántos triángulos se contarán en total? M N Resolución: Sería muy laborioso el conteo si trazamos las 50 rectas de golpe, entonces aplicando lógica inductiva, iremos trazando dichas rectas uno por uno y analizando cada caso: 1 M N Nº de triángulos = 6 = 3(2) Nº de rectas trazadas + 1 2 1 M N Nº de = triángulos = 9 3(3) Nº de rectas trazadas + 1 3 2 1 M N . . . . . . .. 12 = 3(4) .. .. .. 50 2 1 M = Nº de rectas trazadas + 1 Luego : .. .. Nº de triángulos N Nº total de triángulos = 3(51) = 153 \ Respuesta : 153 triángulos Nº de rectas trazadas + 1 99 EJERCICIO 2 Calcular la cantidad total de esferas que hay en el siguiente arreglo triangular. 1 2 3 98 99 100 Resolución: Debido a que la distribución de las esferas responden a una formación triangular, entonces analizaremos, recurriendo a la inducción, los casos iniciales a dicha formación: Números triangulares # de esferas Nº esferas en la base 1 = 1 = 1x2 2 = 2x3 2 Nº esferas en la base 1 + 2 3 = Nº esferas en la base 1 + 2 + 3 6 = = 3x4 2 = 4x5 2 Nº esferas en la base 1 + 2 + 3 + 4 = 10 . . . Luego 1 + 2 + 3 + .... + 100 = 100 x 101 2 1 2 99 100 = 5050 100 101 EJERCICIO 3 EJERCICIO 4 Hallar la suma de todos los elementos de la siguiente matriz: Calcular "n" y dar como respuesta la suma de sus cifras: 1 2 3 4 … 9 10 2 3 4 5 … 10 11 3 4 5 6 … 11 12 4 5 6 7 … 12 13 9 10 11 12 17 18 10 11 12 13 18 19 S=1+3+5+7+9+… "n" términos Resolución: Aplicando inducción tendremos: S = 1 = 1 = 1² = 4 = 2² = 9 = 3² S = 1+3+5+7 = 16 = 1 término Resolución: Sumar los 100 elementos que conforman la matriz va a ser demasiado operativo, aplicando inducción tendremos: S = 1+3 2 términos [ 1 ] ó suma = 1 = (1)³ S = 1+3+5 # filas 3 términos 1 2 2 3 ó suma = 8 = (2)³ # filas 4² 4 términos 1 2 3 2 3 4 3 4 5 .. . .. . ó suma = 27 = (3)³ .. . .. . # filas S = 1 + 3 + 5 + 7 + ... = .. . n² n términos 1 2 … 10 2 3 … 11 3 4 … 12 .. . .. . … .. . 10 11 … \ La respuesta es n² \ suma = (10)³ = 1000 19 # filas EJERCICIO 5 Calcular "E" y dar como respuesta la suma de sus cifras. E = (333 … 333)² \ suma = 1000 200 cifras 102 Resolución: Número de puntos de contacto Por inducción tendremos: 3² = 9 1 2 Scifras = 9 = 9(1) 3 = 3(1) = 3 ( 1 x 2 2 ( 9 = 3(3) = 3 ( 2 x 3 2 ( 18 = 3(6) = 3 ( 3 x 4 2 ( # cifras 1 cifra (33)² = 1089 Scifras = 18 = 9(2) # cifras 2 cifras (333)² = 110889 1 2 3 Scifras = 27 = 9(3) # cifras 3 cifras .. .. . 1 2 3 4 E = (333...333)² = 11...110 88...889 200 cifras .. . .. . .. . .. . 199 cifras 199 cifras Luego : \ Scifras = 9(200) = 1800 # cifras EJERCICIO 6 ¿Cuántos puntos de contacto hay en la siguiente gráfica de circunferencias? 1 2 3 28 29 30 # Total de puntos = 3 \ de contacto ( 29 x 30 2 ( = 1305 EJERCICIO 7 1 2 3 28 29 30 Hallar la suma de cifras del producto siguiente: P = 777 … 777 50 cifras x 999 … 999 50 cifras Resolución: Vamos a proceder a contar, aplicando el método inductivo, es decir, analizando casos simples, cuidando que la formación (distribución de las esferas) se mantenga uniformemente, así: Resolución: Viendo la formación que presenta cada factor, entonces analizaremos la multiplicación para casos más simples, así: 103 Suma de cifras 7 x 9 = 63 ® = 9 = 9(1) EJERCICIO 9 Calcular la suma de cifras del resultado de A 1 cifra 1 cifra 77 x 99 = 7623 ® = 18 = 9(2) A = (777 … 777 + 222 … 2225)² 2 cifras 2 cifras 777 x 999 = 776223 ® = 27 = 9(3) 3 cifras "n" cifras "n - 1" cifras 3 cifras Resolución: Luego: P = 77...776 22...223 ® = 9(50) = 450 49 cifras 49 cifras EJERCICIO 8 El valor de "n" puede ser un valor grande como también un valor pequeño. Para hacerlo más sencillo, vamos a analizar este problema para valores pequeños de "n" (2, 3 y 4); y, al final, después de observar lo que sucede sacaremos una conclusión general. A una hoja cuadrada y cuadriculada con 100 cuadraditos por lado, se le traza una diagonal principal ¿Cuántos triángulos como máximo podrán contarse en total? (77 + 5)² = (82)² = 6724 Resolución: Þ Scifras = 6 + 7 + 2 + 4 = 19 Si tratamos de contar los triángulos uno por uno en el cuadrado de 100 cuadraditos por lado, va a resultar muy agotador. Lo más recomendable sería, en este caso, analizar ejemplos en los cuales el número de cuadraditos sea mucho menor. Aplicando inducción tendremos: (777 + 25)² = (802)² = 643204 Þ Scifras = 6 + 4 + 3 + 2 + 4 = 19 1 1 # total de Ds = 2 = 1 x 2 # de cuadraditos por lados (7777 + 225)² = (8002)² = 64032004 1 2 1 2 # total de Ds = 6 = 2 x 3 # de cuadraditos por lados 1 2 3 1 2 3 1 2 3.. .. .. .. 100 Þ Scifras = 6 + 4 + 3 + 2 + 4 = 19 .. . # total de Ds = 12 = 3 x 4 .. . 1 2 3...... 100 .. . # de cuadraditos por lados A = (77…77 + 22...225)² = 6400...003200...004 "n" cifras \ # total de Ds = 100 x 101 = 10100 "n - 1" cifras "n - 3" cifras "n - 2" cifras cero cero \ Scifras = 19 104 EJERCICIO 10 Calcular la suma de cifras del resultado de: M = (a + 3)(a + 3) … (a + 3)(a + 3)(a + 3) - (a - 3)(a - 3) … (a - 3)(a - 3)(a - 5) 101 cifras 2 101 cifras Resolución: Primero realicemos la diferencia que está dentro del corchete: (a + 3)(a + 3) … (a + 3)(a + 3)(a + 3) — Þ Þ (a - 3)(a - 3) … (a - 3)(a - 3)(a - 5) 6 6 … 6 6 8 101 cifras Entonces: M = (666 … 6668)² 101 cifras Aplicando inducción, tendremos: (68)² = 4624 Scifras = 16 = 6(2) + 4 2 cifras (668)² Nº cifras del número base = 446224 Scifras = 22 = 6(3) + 4 3 cifras (6668)² Nº cifras del número base = 44462224 Scifras = 28 = 6(4) + 4 4 cifras .. .. Nº cifras del número base M = (66 … 668)² = 44 … 44622 … 224 101 cifras 100 cifras 100 cifras \ Scifras = 6(101) + 4 = 610 105 EJERCICIO 11 En la figura, calcular el número total de "hojitas" de la forma indicada: 1 2 3 49 50 51 Resolución: Contar una por una las "hojitas" que conforman la gráfica, sería demasiado cansado y perderíamos mucho tiempo. Si aplicamos inducción, tendremos: Nº "hojitas" = 2 = 1 x 2 Nº circunferencias en la base 1 1 Nº "hojitas" = 6 = 2 x 3 Nº circunferencias en la base 2 Nº "hojitas" = 12 = 3 x 4 Nº circunferencias en la base 1 2 3 Nº total de = 51 x 52 = 2652 "hojitas" 1 2 3 49 50 51 106 EJERCICIO 12 Calcular la suma de los términos de las veinte primeras filas en el triángulo numérico siguiente: F1 1 F2 4 F3 F4 9 4 9 9 saludo 16 16 1 16 Nº de personas 16 2x3 Suma = 9 = 3² = 2 4 4 ( F1 1 F2 4 4 F3 9 9 9 1x2 Nº saludos = 1 = 2 2 ( F2 Nº de personas saludo Resolución: Como nos piden sumar hasta la fila 20, pareciera que la única solución sería aplicar algunas fórmulas del capítulo de series; pero si observamos bien el triángulo numérico, vemos que presenta una ley de formación, la cual la podemos aprovechar aplicando inducción. Nº de filas 2 1x2 Suma = 1 = 1² = F1 1 2 F1 Resolución: Resolviendo el problema aplicando inducción tendremos: 3x4 Suma= 36 = 6² = 2 ( ( 2 Nº saludos = 3 = 2x3 2 2 Nº saludos = 6 = 3x4 2 3 saludo Nº de personas 3 .. 1 2 3 4 4 n-1 n ...... Nº de personas (n-1)n Nº saludos = 2 Nº de filas Por dato del problema tendremos: Nº de filas Nº saludos = 1275 = (n-1)n 2 2 ( 2 ( n(n - 1) = 2550 = 51 x 50 \ Nº de personas: n = 51 F1 1 F2 4 4 9 9 9 F3 Nº de filas 2 Suma= ( 20 2x 21( = 44100 F20 EJERCICIO 14 Dado el esquema: S1: S2: S3: S4: \ Suma de términos : 44100 EJERCICIO 13 A una reunión asistieron cierto número de personas, si cada una fue cortés con los demás y en total se contaron 1275 estrechadas de manos (saludos), averiguar, ¿cuántas personas asistieron? ¿Cuántas bolitas habrá en S12? ...... 107 Resolución: Si contamos las bolitas en los 4 casos particulares dados, tendremos: contarlas una por una, ya que sería un trabajo muy laborioso y correríamos el riesgo de obviar algunas, y dar una respuesta equivocada. Por lo tanto, aplicaremos el método inductivo. Nº de bolitas 1 S1 1 = 2-1 S 2 3 = 2-1 S 3 7 = 2-1 S • Digamos que la palabra a leer sea "IN" 2 letras IN 3 I 4 15 = 2 - 1 4 N -1 2 = 21 formas N 12 \S 2 - 1 = 4096 - 1 = 4095 bolitas 12 EJERCICIO 15 Según el esquema mostrado, ¿de cuántas maneras diferentes se puede leer la palabra "INDUCCION"? I N N D D D U U U U C C C C C C C C C C C I I I I I I I O O O O O O O O N N N N N N N N N • Ahora que la palabra sea "IND": letras IND I N D • D formas D Ahora que la palabra sea "INDU": letras INDU Resolución: I I N N D D D U U U U C C C C C C C C C C C I I I I I I I O O O O O O O O N N N N N N N N N N D U 8 = 2³ N D U U -1 formas D U En el problema : INDUCCION Totalmaneras = 2 Como se puede apreciar, la palabra "Inducción" puede ser leída (siguiendo las líneas punteadas) de diferentes maneras, demasiadas como para -1 4 = 2² N -1 letras = 28 = 256 \ Se puede leer de 256 maneras diferentes 108 EJERCICIO 16 ¿De cuántas maneras distintas se puede leer la palabra "ROMA" en el siguiente arreglo triangular? Como finalmente puedes apreciar, la palabra "ROMA" se lee en dicho arreglo de 15 maneras distintas. Observa bien el conteo en cada caso y contesta las siguientes preguntas: 1. ¿Los números 1; 3; 7 y 15 obtenidos en cada caso, se han escrito en su forma equivalente como potencias de dos menos una constante ¿Por qué o para qué se ha hecho esto? R R O R R O M O R R O M A M O R Resolución: ¿Has visto cómo se ha procedido en el ejercicio anterior? Podemos proceder, ahora, de modo análogo; es decir: Nº Formas 1er. Caso Se lee: "R" ( letra) R 1 = 2 - 1 2do. Caso Se lee: "RO" ( letra) ¯ R¬ ROR ® 3 = 2 - 1 2. ¿Tiene alguna relación el número de letras que se lee en cada uno y el exponente que presenta la respectiva potencia 2? 3. Deduce la expresión matemática que nos brinda el número de formas de leer palabras dispuestas, en arreglos análogos al mostrado, responde la siguiente pregunta: ¿De cuántas maneras distintas se puede leer la palabra "CREATIVO", en el siguiente arreglo? C C R C R 3er. Caso R O R Se lee: "ROM" R O M O R ( letra) C R E R C 7 = 2 - 1 C R E A E R C C R E A T A E R C C R E A T I T A E R C 4to. Caso Se lee: "ROMA" ( letra) C R E A T I V I T A E R C C R E A T I V O V I T A E R C \ Se puede leer de 255 maneras R R O R 15 = 2 - 1 EJERCICIO 17 R O M O R R O M A M O R Lado 1 7 maneras Lado 2 7 maneras Centro 1 Sabiendo que: A1 = 1 x 100 + 50 A2 = 2 x 99 + 49 Se calcula, análogamente igual al lado 1 A3 = 3 x 98 + 48 . . . . . . . . . Calcular: A20 109 Resolución: EJERCICIO 19 Analizando los casos dados como datos, tendremos: Hallar: 4 E= F180 + S137 si: suma 101 = A x 100 + 50 -50 suma 101 = A x 99 + 49 S1 = 1 F1 = 2 S2 = 1 + 1 F2 = 2 + 2 S3 = 1 + 2 + 1 F3 = 2 + 4 + 2 S4 = 1 + 3 + 3 + 1 .. . F4 = 2 + 6 + 6 + 2 .. . -50 suma 101 = A Resolución: x 98 + 48 Analicemos los casos dados: -50 .. . suma 101 A x = + S1 = 1 = 2º F1 = 2 = 2¹ S2 = 2 = 2¹ F2 = 4 = 2² S3 = 4 = 2² F3 = 8 = 2³ S4 = 8 = 2³ .. . F4 = 16 = 24 .. . -50 Þ S137 = 2136 Þ F180 = 2180 suma 101 \ A = 4 x 81 + 31 = 1651 \E= -50 F180 S137 4 = 2180 2 136 4 = 244 = 211 = 2048 EJERCICIO 18 Si: EJERCICIO 20 An = (-1)n + 1 Si: AA + DD + UU = ADU Sn = A1 + A2 + A3 + … + An calcular: E = A² + D² + U² Hallar : S21 - S20 Resolución: Resolución: Deduzcamos los valores de A, D y U a partir de criterios generales: Calculando primero S21 y S20 obtenemos: S21 = A1 + A2 + A3 + … + A19 + A20 + A21 S20 = A1 + A2 + A3 + … + A19 + A20 Þ S21 - S20 = A21 = (-1)21 + 1 = - 1 + 1 \ S21 - S20 = 0 1 — . AA + DD UU ADU 110 I. El máximo valor que puede asumir la suma de 3 números de 2 cifras es: 3(99) = 297 Entonces en el resultado ADU, la cifra "A" puede ser 2 ó en todo caso 1. II. Sumando las cifras de las unidades, tendremos: A + D + U = ...U ...0 Þ A + D = 10, entonces llevaré 1 a las decenas Resolución: Para mayor comodidad, numeremos las filas de esta operación: I II III IV V VI * * * * - 2 * 0 9 - * * * * * * - 5 * 325 1** * * 5 * * * - - Nos damos cuenta que como esta división no tiene residuo, bastaría con sólo conocer las cifras del cociente para resolver este problema. Entonces: III. Sumando en la columna de las decenas: 1 + A + D + U = AD A+U=9 10 10 + D = AD 1D = AD I. Para que el residuo sea cero, la segunda cifra de la fila VI debe ser 5, y para que resulte 5, la tercera cifra del cociente debe ser 2, pues es la única manera que: (2 x 325 = 650). 5 2 6 5 0 325 162 3 2 5 2 0 1 5 A=1 1 9 5 0 - - 6 5 0 Pero: A + D = 10 A + U = 9 Þ A = 1, D = 9, U = 8 \ A² + D² - U² = 1² + 9² - 8² = 18 EJERCICIO 21 Reconstruir la siguiente operación de división e indicar la suma de cifras del dividendo, si cada * representa un dígito cualquiera. * * * * - 2 * 0 9 - * * * * * * - 5 * * * 5 * * * - - 6 5 0 D = 9 U = 8 325 1** - - - II. Para que la segunda cifra de la fila IV sea 9, la segunda cifra del cociente debe ser 6: ya que 325 x 6 = 1950, conociendo ya las cifras del cociente, la operación reconstruida sería: \ Suma de cifras del dividendo = 5 + 2 + 6 + 5 + 0 = 18 EJERCICIO 22 Si : abc + cba = .......8 abc - cba = .......8 Calcular el máximo valor de : a + b + c 111 Resolución: Entonces: Como tenemos la suma y diferencia de los mismos números, entonces: N3 + N6 + N9 + ........ + N90 = ...abc 30 sumandos (...376) + (...376) + (...376)+…+(...376) = ...abc 30 sumandos abc + cba = ...8 abc - cba = ...8 30 x (...376) = ...abc 2(cba) = …0 …1280 = ...abc a = 2; b = 8; c = 0 \ a + b + c = 2 + 8 + 0 = 10 a=0 ó a=5 como a ¹ 0, entonces: a = 5 EJERCICIO 24 Luego: Si: n + nn + nnn + nnnn + … + nnn … nnn = ......xy9 abc + cba = ...8 17 sumandos como a = 5, entonces: c = 3 Calcular: E = (n - y)(x-y) Como nos piden el máximo valor de: a+b+c, entonces b tomará su máximo valor, es decir: b=9 \ a + b + c = 5 + 9 + 3 = 17 Resolución: Si colocamos a los 17 sumandos, uno debajo del otro, tendremos: I. EJERCICIO 23 3 6 9 90 (17 x 7 = 119) "dejamos 9 y llevamos 11" = ...........abc II. Resolución: Para hallar: a, b y c, habrá que hallar las potencias de N³, entonces: N3 = .....376 (dato) 6 3 3 9 3 6 N = N x N = (...376) x (...376) = ...376 11 nn...nnnnn Al sumar las 16 cifras de las ............xy9 decenas, más 11 que "llevamos" de la operación anterior, obtenemos: 16 x n + 11 que es 16(7) + 11 = 123; y = 3 "Dejamos 3 y llevamos 12" III. Al sumar las 15 cifras de las centenas, más 12 que "llevamos" de la operación anterior, obtenemos: N = N x N = (...376) x (...376) = ...376 12 3 9 N = N x N = (...376) x (...376) = ...376 .. .. N 90 = .....376 n + nn nnn nnnn 12 17 x n = ...9 Þ n = 7 Si: N³ = ...376, calcular: a + b + c donde: N + N + N + ....... + N Al sumar las 17 cifras de las unidades obtendremos: 15 x n + 12 = ...x Þ x = 7 (15 x 7 + 12 = 117) "Dejamos 7 y llevamos 11" \ E = (n-y)(x-y) = (7 - 3)(7-3) = 44 = 256 112 Entonces: EJERCICIO 25 d Si: E= abcd = d, calcular: abc x 512 a.b+d c abc x 2 productos abc x 1 parciales abc x 5 Resolución: De la última expresión, nos damos cuenta que un d número elevado a él mismo (d ) debe dar como resultado un número de cuatro cifras (abcd) y, como "d" es una cifra, su valor oscila de 0 a9, entonces: Por dato, tenemos: abc x 2 + abc x 1 + abc x 5 = 3496 8(abc) = 3496 - abc = 437 Reemplazando, luego, en el producto original: abc x 512 obtenemos : 1 2 3 4 5 1 = 1; 2 = 4; 3 = 27; 4 = 256; 5 = 3215; 66 = 46656 Viendo los resultados, el único valor que cumple con la condición anterior es d = 5, entonces: abc x 512 = 437 x 512 = 223744 \ Scifras = 2 + 2 + 3 + 7 + 4 + 4 = 22 EJERCICIO 27 Si: abc x a = 428 abc x b = 214 a=3 c=2 5 5 = 3125 \ E= axb+d c = b=1 d=5 3x1+5 8 = = 4 2 2 abc x c = 856 Calcular: E = (a x b x c)² Resolución: Si acomodamos, correctamente, cada producto obtendremos: EJERCICIO 26 Hallar la suma de cifras del resultado de multiplicar "abc x 512", sabiendo que la suma de los productos parciales de esta multiplicación resulta 3496. abc x a = 428 = 214 x 2 abc x b = 214 = 214 x 1 a = 2 b = 1 c = 4 abc x c = 856 = 214 x 4 Resolución: Antes de entrar al problema en sí, hagamos un ejemplo previo: 237 x 94 948 2133 22278 \ E = (a x b x c)² = (2 x 1 x 4)² = 64 EJERCICIO 28 237 x 4 productos 237 x 9 parciales Producto Final Si: abcde + edcba = 876... y además: a < b < c < d < e Calcular: E = a² + b² + c² + d² + e² 113 Resolución: 5(2x² + 30) + 10(15 + x²) = 420 Disponiendo la operación verticalmente: abcde edcba 876-- 10(x² + 15) + 10(x² + 15) = 400 + 20 + 10(x² + 15) + 10(x² + 15) = 400 + 400 I. La suma de dos números iguales siempre da un valor par, y como la cifra de las centenas del resultado es 6, concluimos que c = 3 ó c = 8. Este último valor no puede ser porque si c = 8, según la desigualdad, "e", como mínimo, tendría que ser 10 y eso sería absurdo, entonces: c = 3 II. Por la desigualdad, concluimos: 2 Þ 10(x² + 15) = 400 ® x² + 15 = 40 Þ x² = 25 Þ x = 5 Reemplazando : \ 2x + 5 = 2(5) + 5 = 15 EJERCICIO 30 a<b<c<d<e 1 (Por comparación) ¿Cuál es el número de 5 cifras que, multiplicado por 22, nos da un producto cuyas cifras son todas 8? 3 III. Si reemplazamos estos valores en la operación, tendremos: Resolución: Supongamos que el número de 5 cifras sea abcde; entonces, por condición del problema, tendremos: abcde x 22 = 88...88 (la cantidad de cifras del producto es desconocida), despejando se tiene: 1 2 3 d e + e d 3 d 1 8 7 6 - d = 5 e = 7 abcde = \ E = a² + b² + c² + d² + e² 88...88 22 = 1² + 2² + 3² + 5² + 7² = 98 EJERCICIO 29 + Calcular el valor de "2x + 5", si xÎZ y además 5(2x² + 30) + 888888 22 88 40404 - - 88 abcde 88 - - 88 88 -- \ abcde = 40404 10(15 + x²) = 420 EJERCICIO 31 + Resolución: Si comenzamos a operar la expresión anterior, nos vamos a complicar demasiado. Mejor podríamos comenzar a deducir a partir de que "x" es un entero positivo y obtendremos: Si: a, b y c Î Z y se cumple que: a + b + c = 11 a² + b² + c² = 49 Calcular: E = (a + b)² + (b + c)² + (c + a)² 114 Resolución: 2(a x b) = da Si procedemos a operar, el ejercicio resulta tedioso; pero si comenzamos a deducir a partir de que a, b, c Î Z+ obtendremos: a² + b² + c² = 49 (la suma de tres cuadrados perfectos resulta 49) 2 8 32 Þ b = 8 ; d = 3 III. b² = ec 8² = 64 Þ e=6 ; c=4 \ a0b + cdaec = 208 + 43264 = 43472 1², 2², 3², 4², 5², 6², 7²,... EJERCICIO 33 ¿Cuántos triángulos hay en total en f(20)? suma = 49 Entonces : Verificando: a² + b² + c² = 49 a + b + c = 11 2² + 3² + 6² = 49 2 + 3 + 6 = 11 \ E = (a + b)² + (b + c)² + (c + a)² = 5² + 9² + 8² = 170 EJERCICIO 32 Hallar: a0b + cdaec, si (a0b)² = cdaec , , f(1) , f(2) f(3) Resolución: Según lo que se observa nos podemos formar una idea de cómo será el gráfico que corresponde a f(20); pero dibujar el gráfico y contar los triángulos que hay en él sería un trabajo demasiado tedioso; por lo tanto, aplicamos el método inductivo. Además: 0 = cero y las letras diferentes tienen valores diferentes. Resolución: Número de triángulos (a0b)² = a0b x a0b = cdaec Entonces: a0b x a0b axa mec f(1) f(2) f(3) 1 2 3 4+1 4+4+1 4 + 4 + 4 +1 Los Los El pequeños pequeños grande Los El medianos grande 20 bxb \ f(20) 4 + 4 + 4 ...... 4 + 1 = 81 0m cdaec Donde: I. b² = ec ; m = a x b ; a² = c Þ b = 4, 5, 6, 7, 8, 9 Þ a = 1, 2, 3 EJERCICIO 34 Hallar el valor de "S": 1 1 1 1 1 S= + + + +…+ 1x2 2x3 3x4 4x5 99 x 100 par II. m + m = da Þ 2m = da par Þ a=2 Resolución: Son muchos los números que debemos sumar por lo cual, hacerlo de manera directa, nos demandaría demasiado tiempo, es por eso que aplicaremos el método inductivo. 115 S= 1 1 = 1x2 2 11 + 22 x a = … a a = 9 11 + 22 x 9 = 20 9 S= 1 1 2 + = 1x2 2x3 3 S= 1 1 1 3 + + = 1x2 2x3 3x4 4 .. . 1 1 \S = 1 x 2 + 2 x 3 Nos piden: M= 1 1 99 +…+ = 3x4 99 x 100 100 + Como se puede observar, el resultado de sumar este tipo de números está en función a los factores que aparecen en el denominador de la última fracción. ab - ba 95 - 59 = M= 36 = 6 EJERCICIO 36 Halle la cantidad total de "palitos", en la siguiente figura: EJERCICIO 35 Si: b + ab + bab + abab + babab +...+ baba...bab = ...ab 23 cifras Calcular: M= ab - ba Resolución: 2 1 3 4 99 100 Colocamos los números en forma vertical. Resolución: 11 b Si contamos, uno por uno la cantidad de "palitos" que conforma la figura, sería demasiado extenso. Si analizamos casos "pequeños", tendremos: + ab bab 23 sumandos abab ... Þ Nº de "palitos" = 3 = x3 1 1 aba...bab .........ab 2 Producto de los últimos dos números entre 2 En el orden de las unidades: 23 x b = … b 23 x 5 = 11 5 b = 5; Þ Nº de "palitos" = 9 = 3x3 "Llevamos" 11 siguiente orden 1 En el orden de las decenas: 2 3 Producto de los últimos dos números entre 2 116 I. Al sumar las cifras de las unidades obtendremos: Þ Nº de "palitos" = 18 = 3 x 6 1 2 3 4 s + q + p + r = ......c Producto de los últimos dos números entre 2 28 = ......c "De aquí c = 8 y llevamos 2" II. Al sumar las cifras de las decenas, más 2 que llevamos en la operación anterior obtendremos: s + q + r + q + 2 = ........b 1 2 3 4 98 99 100 30 99 x 100 = 4950 2 Luego: = ........b "De aquí b = 0 y llevamos 3" 3(99 x 100) Þ Nº de palitos = 3 x 4950 2 \ Nº de palitos = 14850 III. Al sumar las cifras de las centenas más 3 que llevamos en la operación anterior obtendremos: q + r + p + s + 3 = ........d EJERCICIO 37 Si: p + q = 12 y r + s = 16 31 = ........d además: "De aquí d = 1 y llevamos 3" qqss + mpq + pprp + ssqr = addbc calcular : (a + b + c - d)² Resolución: Colocamos los números en forma vertical IV. Al sumar las cifras de los millares ocurre lo mismo que las cifras de las centenas, llevando 3 a la cifra de unidad de millar, de aquí a = 3. \ (a + b + c - d)² = (3 + 0 + 8 - 1)² qqss + mpq pprp ssqr addbc = 100 EJERCICIO 38 Si : como : p + q = 12 r + s = 16 Þ m.n = p, halle: p; además: p + q + r + s = 28 si : m² - p² + n² = 1296 1 1 1 + m² n² p² 117 Resolución: Al operar la siguiente expresión se tiene que: (m² - p² + n²) m² n² p² = 1296 n² p² + p² m² - m² n² 2 x n x n - 2 n x + n x 2 = 0 2 x n n n = 0 4 Además : mn = p, entonces: m² n² = p Al extraer la raíz cuadrada obtenemos: x n = 0 Þ x = n n x Reemplazando se tiene que: 6 (m² - p² + n²) . p = 1296 n² p² + p² m² - p4 \ A= x n = n n Factorizando: 3 -3 n x n x 2 + 2 + n n n x 3 + 3 + n n +3 6 (m² - p² + n²) . p = 1296 = 6 6 (n² + m² + n²) . p 4 4 3 n -3 n +3 4 p =6 = 3 \ p=6 EJERCICIO 40 EJERCICIO 39 x n Si : 2 n x + Si: 8n - 8n-1 = 14, entonces (3n)3n es igual a: 2 = 2 Resolución: calcule : A= x n 3 - 3 n x n x + 2 + n x n n-1 8 -8 3 +3 n 8 - = 14 8n = 14 (Multiplicando todo por 8) 8 8 Resolución: n+1 n - 8 = 8 . 14 Recordar: n 8 = 16 Dándole forma al dato: 3n 2 =2 (Expresando como potencia de 2) 4 3n = 4 x n 2 + n x 2 = 2 x n n x , despejando \ (3n)3n = 44 = 256 118 PRACTICANDO 01 1. Calcular el valor M y dar como respuesta la suma de sus cifras: M = (666666666666)² A) 102 D) 110 B) 140 C) 108 E) 111 6. En el siguiente gráfico, ¿cuántos triángulos equiláteros se formarán, en total, al unirse los centros de tres circunferencias vecinas inmediatas? Obs.: De la forma indicada 2. Calcular la suma de cifras del resultado: A = 555...555 x 999...999 100 cifras A) 1 D) 90 B) 10 3. Si: A = (333...333)² y 100 cifras C) 100 E) 900 61 cifras 31 cifras Calcular la diferencia entre la suma de cifras del resultado de A y la suma de cifras del resultado de B. A) 279 D) 828 B) 549 3 1 2 19 20 21 B = (666...666)² C) 270 E) 720 A) 20 D) 441 4 B) 21 C) 400 E) 360 7. ¿Cuántos triángulos se pueden contar, como máximo, en la siguiente figura? 4. Calcular la suma de cifras del resultado de: A= 111 … 111 - 222 … 222 "2n" cifras A) n D) n² B) 3n "n" cifras C) 6n E) 2n 5. ¿Cuántas "cerillas" conforman la torre mostrada? 1 2 3 A) 5500 D) 5253 4 48 49 50 51 B) 5000 C) 5050 E) 5250 8. Calcular la suma de los términos de la fila 50. Fila Fila Fila Fila 1 2 3 4 A) 20 D) 200 1 2 3 4 1 3 5 7 9 11 13 15 17 19 19 20 21 B) 21 C) 210 E) 420 A) 9750 D) 75200 B) 12500 C) 25000 E) 125000 119 9. Si: a + b + c = 0 Calcular la suma de cifras de A : A = (xxx … xxx)² 100 cifras sabiendo, además que: a² b² c² x= + + bc ac ab A) 90 D) 900 B) 989 C) 99 E) 199 10. Calcular la suma de cifras del resultado de "A". A = (999 … 9995)² 101 cifras B) 925 A) 900 D) 90 A) 2500 D) 2000 B) 1900 C) 625 E) 907 34 36 36 38 A) 441 D) 400 2 3 18 19 20 B) 225 B) 64 C) 81 E) 72 14. Si: a5 x a6 x a7 x a8 + 1 = 2161 Calcular: M = a + aa + aaa + aaaa + .... A) 4936 D) 4938 B) 4856 C) 4836 E) 4746 15. ¿Cuántos "palitos" se trazaron para construir el siguiente arreglo? 1 2 3 4 5 48 49 50 C) 1650 E) 3600 12. Calcular el número total de triángulos de la forma D y Ñ en la siguiente figura: 1 A) 49 D) 100 "a" sumandos 11. Hallar la suma de los elementos de la siguiente matriz de 10 x 10 2 4 6 18 20 4 6 8 20 22 6 8 10 22 24 18 20 22 20 22 24 13. Calcular la suma de cifras del resultado de efectuar: E = 81(12345679)² C) 324 E) 300 A) 3600 D) 3725 B) 3675 C) 2550 E) 3625 16. ¿Con cuántos "palitos" se formó la siguiente figura? 1 2 3 4 5 A) 11000 D) 10100 96 97 98 99 100 101 B) 10010 C) 10200 E) 10101 120 17. Para construir el siguiente castillo se utilizaron "cerillas", ¿cuántas se emplearon en total? 1 2 3 A) 10000 D) 20400 99 100 101 B) 16000 C) 25000 E) 20300 18. Hallar la suma de cifras del resultado de la siguiente operación: 999 … 99 - 1999 998 2(n - 1) cifras A) 3n D) 9n B) 6n n cifras 20. En el siguiente triángulo, ¿cuántas bolitas sombreadas hay? 98 99 100 1 2 3 A) 2550 D) 5100 B) 2500 C) 2250 E) 2555 21. Determinar: "P + U + C", si PUC + CUP = 888 Además: P - C = 4 A) 10 D) 13 B) 14 C) 11 E) 18 C) 6(n + 1) E) 9(n - 1) 22. Al multiplicar un número de 7 cifras consecutivos por 13, el resultado termina en 7. ¿Cuál será la diferencia entre la suma de cifras del resultado, con la suma de cifras del número de 7 cifras? 18. Si: M(1) = 4 x 1 + 1 M(2) = 8 x 4 + 8 A) 0 D) 14 M(3) = 12 x 9 + 27 Calcular el valor de x, si M(x) = 4 x 104 B) 1 C) 35 E) 13 23. Si. ANITA x 8 = PEPITO , 0 = CERO Hallar: M = A + N + I + T + E + P A) 15 D) 20 B) 18 C) 23 E) 21 A) 20 D) 27 B) 24 C) 35 E) 28 121 24. Reconstruir la siguiente operación e indicar la suma de cifras del resultado. Cada asterisco representa un dígito cualquiera. B) 22 E= A) 10 D) 6 **** x *6* *84* 1**** **** **5129 A) 21 D) 24 28. Calcular la suma de cifras del resultado de: 10305050301 + 2040604020 B) 9 C) 12 E) 8 29. Un número de 4 cifras de la forma abc6, elevado al cuadrado, termina en abc6, Calcular: a + b + c C) 23 E) 25 25. Calcular la suma de cifras del cociente, en la siguiente división: A) 17 D) 20 B) 18 C) 19 E) 21 30. Calcular: (A - M - N)1997 si se sabe que: 1A + 2A + 3A + … + 9A = MN1 * * * * * * * * * * * 8 * * * * * - - - * * - * * * * * * - - 1 A) 0 D) 3 B) 1 C) 2 E) 4 31. En la siguiente división, hallar la suma de las cifras del dividendo: A) 20 D) 30 B) 21 C) 26 E) 32 2 * * * * * * * * * * 3 * - - * * * 5 - * * 5 * - - 26. Hallar la última cifra del resultado de: E = 367131 + (82519 + 1)(26² - 1) A) 1 D) 4 B) 1 C) 3 E) 5 27. Si: SIETE + TRES = 100000 hallar SEIS, además: I = E y T = R A) 21 D) 18 B) 37 32. Si: A + U = D y U + D = 17 hallar la suma de las cifras del resultado de: E = AU x (AA...AA)² - (DD...DD)² + (UU...UU)² 8 cifras A) 8128 D) 9339 B) 8118 C) 9229 E) 9119 C) 25 E) 15 A) 49 D) 72 B) 54 8 cifras C) 64 E) 80 8 cifras 122 33. En un examen, las respuestas a las cinco primeras preguntas son: a, b, c, d, e; para las siguientes 10 son: a, a, b, b, c, c, d, d, e, e; para las siguientes 15 son: a, a, a, b, b, b, c, c, c, d, d, d, e, e, e; y así sucesivamente. Entonces, la respuesta a la pregunta 90, es: A) a D) d 34. Si: B) b A2 C) c E) e 37. Se tiene un número de 3 cifras que comienza en 5 y acaba en 2; dichas cifras son cambiadas por 1 y 8, respectivamente. ¿En cuánto ha disminuido dicho número? A) 388 D) 280 B) 432 C) 406 E) 394 38. Si: (a + b + c)² = a25 Calcular: M = ab3 + c2b + 4ac + bca =3 A) 1475 D) 1575 1A Calcular: E = 2(A + 3) + 7 A) 4 D) 21 B) 7 B) 370 A) 1 D) 2 C) 535 E) 337 B) 27 111 términos 7 + 77 + 777 + 7777 + … + 777..77 = .....mnpq = 36 sumandos B) 5 C) 36 E) 3 40. Calcular: a + b + c + d, si: a y c < 6 ; b yd < 8 Además: 131² + 133² + 135² + 231² + 233² + 235² + … = 36. Efectuar la siguiente suma y hallar: m+n+p+q A) 7 D) 12 C) 2088 E) 1988 39. Poseo cinco dígitos, pero si me restaras la unidad, ya no tendría cinco, sino solamente cuatro, ¿quién soy? (Dar como respuesta la suma de cifras del número) C) 14 E) 20 35. Si: ababa x 6 = 212118, hallar: aab + ab A) 335 D) 730 B) 1685 C) 5 E) 14 ...ab + ...cd A) 2 D) 7 B) 3 C) 5 E) 9 CLAVES 1 C 11 D 21 E 31 E 2 E 12 C 22 A 32 C 3 C 13 C 23 C 33 C 4 B 14 A 24 E 34 D 5 E 15 B 25 C 35 B 6 C 16 D 26 A 36 E 7 C 17 E 27 E 37 E 8 E 18 E 28 D 38 C 9 D 19 D 29 C 39 A 10 E 20 A 30 B 40 D 123 PRACTICANDO 02 1. En el siguiente arreglo, ¿de cuántas formas se puede leer la palabra Roma? A A A A A) 27 M M M B) 20 A O O A C) 28 M R M D) 21 A O O A E) 19 M M M A A A A 6. En el siguiente arreglo, 4 8 halle las sumas de 8 12 todos los números. 12 16 16 20 A) 4000 B) 4200 40 44 C) 4700 D) 5200 E) 47211 2. Halle la suma de cifras del producto 7. Halle el valor de la suma 40 44 48 52 48 52 76 ABCD + EFGH + IJKL + MNOP *4* 2** 1*** ***4* 6*4** 9**50 A) 18 B) 24 C) 25 D) 12 E) 30 12 16 16 20 20 24 24 28 si se cumple que: AB + EF + IJ + MN = 347 CD + GH + KL + OP = 305 3. En la siguiente figura, halle la cantidad de palitos. A) 36405 D) 43215 B) 46225 C) 64555 E) 35005 8. Si MIA x 999 = .......1648 1 A) 702 D) 901 2 3 . . . .18 B) 709 calcule 19 MAMA x 99 20 A) 319968 D) 47211 C) 800 E) 699 B) 53222 C) 432412 E) 66647 9. En la figura, halle la cantidad de palitos 4. ¿De cuántas maneras diferentes se puede leer TROTAMUNDOS? N OT M UNDO R T O A U D S R T M N O O U D N A) 130 B) 128 C) 135 D) 166 E) 120 5. En la figura al unir los centros de las circunferencias, halle el número de triángulos simples que se forman A) 3600 B) 4200 C) 3500 D) 4100 E) 2460 1 2 3 A) 7000 B) 7198 C) 7411 D) 6852 E) 6421 2 3 4 57 58 59 60 10. En el siguiente arreglo, halle E = (A + B) - (C + D). Si se tiene 77 sumandos A) 14 B) 9 C) 5 D) 6 E) 4 60 61 1 7777 ....... 7777 + 777 7777 ........................ ........................ 777 77 7 ...........DCBA 124 11. Si 17. Si 1 x 2 x 3 x 4 x 5 x 6... x 50 = N x 10 x a-b=b-c= -y 10 donde N no es múltiplo de 5, halle B) 64334 6 Calcule M = [(a - c)6 + (b - c)6 + (a - b)6] + 6 XYOX + XOYY + YXXX + Y47Y A) 25814 D) 11424 6 C) 48624 E) 74284 A) 72 D) 3 B) 66 C) 60 E) 18 12. Halle el valor de R si 2 4 8 1024 R = 2(3+1)(3 +1)(3 +1)(3 +1)...(3 1024 2048 A) 3 246 D) 3 13. Si: B) 3 +1)+1 512 C) 3 1152 E) 3 abcd x 4 = … 792 18. Sabiendo que (a + 2 ab + b)(a - 2 ab + b) = 0 halle el valor de abcd x 5 = … 370 halle las tres últimas cifras del siguiente producto A) 315 D) 716 B) 308 C) 158 E) 324 A= a² + 2b² a² + b² + A) 17 D) 32 a² + 4b² a² + b² + a³ + 8b³ a³ + b³ B) 16 a4 + 16b4 + 4 4 a +b C) 25 E) 8 14. Calcule el valor de R= (409) x (391) + 81 (115) x (85) + 225 A) 3 D) 4 B) 6 19. Calcule la suma del resultado de C) 5 E) 2 2 A = (4444...448)² - (4444...447)² + 1111...1110 100 cifras 15. Halle la suma de cifras de la siguiente 40 40 expresión: A = (10 + 1)(10 - 1) A) 700 D) 720 B) 640 C) 599 E) 761 16. Si cada asterisco es una cifra A) 9 D) 10 100 cifras B) 8 100 cifras C) 6 E) 12 20. Si B = 1 x 1! + 2 x 2! + 3 x 3! + … + 100 x 100! abc - cba = 3** halle el valor de B. abc - cba = *35* halle 2a + b + c A) 18 D) 30 B) 20 C) 27 E) 33 A) 102! - 1 D) 122! - 3 B) 100! - 1 C) 101! - 1 E) 99! + 2 125 PRACTICANDO 03 PROBLEMA 01 PROBLEMA 04 En la siguiente sucesión determinar el número de círculos sin pintar en la colección de círculos que ocupe el décimo lugar. Calcular : 22002 1 + (3 x 5 x 17 x .....) 2002 factores A) 1 D) 2002 A) 201 D) 181 B) 131 C) 151 E) 231 B) 2 C) 32 E) 2003 PROBLEMA 05 Calcular el número total de hexágonos que se pueden contar, considerando el tamaño que se indica en la figura PROBLEMA 02 Hallar el número total de palitos A) 1250 B) 1225 C) 1500 D) 1600 E) 1275 1 2 A) 250 D) 5050 3 1 2 3 51 52 53 4 5 . . . . . . . . 46 47 48 49 50 B) 2450 C) 1324 E) 1275 PROBLEMA 06 En la siguiente gráfica ¿Cuántas bolitas sombreadas hay? PROBLEMA 03 Calcular la suma de cifras del resultado de la siguiente expresión: (999 ...... 999)³ 2002 Cifras Indicar la última cifra de dicha suma A) 6 D) 0 B) 8 C) 4 E) 1 1 2 3 A) 1500 D) 1000 98 99 100 B) 1550 C) 2501 E) 5050 126 PROBLEMA 07 PROBLEMA 07 Cuántas cajitas de la forma se han utilizado en la construcción de la siguiente torre En la siguiente gráfica ¿Cuántos cuadritos sombreados hay? 1 2 3 A) 280 B) 390 C) 410 D) 401 E) 400 8 1 2 3 7 6 5 4 3 2 1 37 38 39 C 49 50 PROBLEMA 08 ¿Cuántos triángulos se pueden contar en la siguiente figura? B) 400 A A) 600 D) 625 C) 441 E) 675 PROBLEMA 11 A) 3775 B) 2105 C) 5050 D) 2500 E) 1275 Halle el número total de palabras "SAN MARCOS" en: 1 2 3 S A N M A R C O S 48 49 50 PROBLEMA 09 ¿Cuántos cerillas se utilizan para formar desde la figura (I) hasta la figura (20)? A) 256 D) 225 F(I) A N M A R C O S O N M A R C O S O C M A R C O S O C R B) 512 A R C O S O C R A R C O S O C R A M C O S O C R A M N O S O C R A M N A S O C R A M N A S C) 511 E) 1023 F(II) F(III) PROBLEMA 12 A) 6160 D) 6170 B) 6140 C) 6110 E) 6180 Hallar la cantidad total de palabras "INGENIO" que se puede leer en la siguiente figura (uniendo letras vecinas consecutivamente) 127 0 0 0 0 A) 192 B) 189 C) 63 D) 255 E) 8 0 0 0 I I N 0 I N E I I N E G N 0 I N E G N E I I N E G N I G N 0 PROBLEMA 15 0 I N E G N E I 0 I N E G N 0 0 I N E I 0 I N 0 0 I 0 ¿De cuántas maneras diferentes se puede leer la palabra "RAZONANDO", uniendo círculos consecutivos? R A A A) 25 Z Z Z B) 21 OOOO C) 75 N N N N N D) 70 A A A A E) 81 N N N D D O PROBLEMA 13 ¿De cuántas formas consecutivas diferentes se puede formar la palabra "RAZONA", uniendo las letras en forma consecutiva? R RAR RAZAR RAZOZAR RAZONOZAR RAZONANOZAR A) 64 B) 63 C) 127 D) 31 E) 128 CLAVES 01) B 02) C 03) A 04) B 05) E 06) C 07) E 08) A 06) A 10) D 11) B 12) B 13) B 14) D 15) D PROBLEMA RECREATIVO: PROBLEMA 14 Calcular el número de rombos con un cuadrado pequeño interior que se forman al unir los centros de todos los cuadrados de la figura. Mover dos palitos de fósforos, de tal manera que el recogedor quede de la misma forma pero con el papel fuera de él: PROBLEMA RECREATIVO: Moviendo tres palitos de fósforo, formar 1 2 2001 2002 2003 3 cuatro triángulos equiláteros: A) 20030 D) 100404 B) 40060 C) 100404 E) 100020 128 PRACTICANDO 04 1. Si se cumple que M(1) = 2 + 1 - 1 M(2) = 4 + 4 ÷ 3 M(3) = 6 X 9 - 5 M(4) = 8 + 16 ÷ 7 5. Halle la suma de todos los elementos de la fila 20 en el siguiente arreglo triangular 1 Fila 1 2 3 Fila 2 3 4 5 Fila 3 Fila 4 4 5 6 7 5 6 7 8 9 Fila 5 halle M(19) A) 348 D) 286 B) 362 C) 452 E) 456 A) 590 D) 480 B) 610 C) 720 E) 350 6. ¿Cuántos palitos conforman la siguiente torre? 2. Halle el valor de E 1 + 3 + 5 + 7 + … + 2001 E= 2 + 4 + 6 + 8 + … + 2002 A) 1001 1002 D) 2000 2001 B) 2001 2002 C) 1001 2000 E) 1000 1001 1 2 3 4 A) 1600 D) 2500 B) 1800 3 4 5 20 21 22 20 21 22 39 A) 441 D) 4000 2 3 4 B) 8000 C) 2100 E) 1900 7. ¿De cuántas formas distintas se puede leer SAN MARCOS en el siguiente arreglo? S 3. Halle la sua de todos los elementos de la siguiente matriz 1 2 3 47 48 49 50 A N M A R C S C) 2000 E) 4441 M A R A R C N M M A R C A R C R C O O O O O O O O S S S S S S S A) 256 D) 128 C A N C B) 1024 S C) 64 E) 512 8. ¿Cuántos triángulos hay en total en f(20)? 4. Halle el valor de la siguiente expresión n sumandos f(1) (1 x 3 - 3 x 5 - 5 x 7 - ...) - n 1² - 2² - 3² - … A) 81 D) 68 n sumandos A) 1 D) 4 B) 2 C) 3 E) n n² - 1 f(2) B) 84 f(3) , .... , .... C) 80 E) 76 9. ¿Cuántos paralelogramos de la forma y tamaño de los que aparecen sombreados hay en total en la siguiente figura? 129 15. Si: 1 2 N x 23 = ....927 3 4 N x 25 = ....225 5 halle las 3 últimas cifras de N x 42 y dé como respuesta la suma de dichas cifras. 50 51 A) 3125 D) 2550 B) 625 A) 12 D) 13 C) 1225 E) 2415 B) 9 16. ¿Cuál es la suma de cifras del producto 15 10. Halle SEIS si SIETE + TRES = 100000 y T=R I=E A) 8118 D) 1881 B) 9119 C) 9339 E) 3333 11. Si abc - mn4 = cba, además a + b + c = 20 c halle a-b A) 1 B) 2 C) 3 D) 4 E) 5 12. Si ADCV(99999999) = ....3518 halle A + D + C + V A) 20 D) 18 B) 24 C) 12 E) 25 13. Halle la suma de las cifras del resultado del C) 10 E) 15 (10 - 1)(10 15 A) 300 D) 450 + 1)? B) 270 17. Si se cumple que f(x + 1) = f(x) + 2 x + 1 y halle f(50) A) 525 D) 1600 C) 150 E) 420 f(1) = 1 B) 2500 C) 1875 E) 1500 18. Halle la suma de cifras del resultado de la siguiente operación S = 555 … 555 + 777 … 777 + 999 … 999 300 cifras 299 cifras 298 cifras multiplicar abc x 512 sabiendo que la suma de los productos parciales sumados convencionalmente nos da 4096. A) 32 D) 48 B) 19 C) 25 E) 12 A) 705 D) 684 B) 816 C) 902 E) 848 19. Efectúe y dé como respuesta la suma de cifras 14. Al dividir abcd entre 4, el cociente es A = (111 … 112)² - (111 … 110)² dcba y el resto es cero. Halle E = a + b + c + d A) 15 D) 17 B) 14 100 cifras C) 16 E) 18 A) 100 D) 400 100 cifras B) 200 C) 300 E) 500