UNIVERSIDAD DE GUAYAQUIL
VICERRECTORADO DE FORMACIÓN
ACADÉMICA Y PROFESIONAL
DIRECCIÓN DE ADMISIÓN Y NIVELACIÓN
Cdla. Universitaria Salvador Allende
www.ug.edu.ec
www.admisionynivelacion.ug.edu.ec
Guayaquil - Ecuador
FACULTAD DE INGENIERÍA INDUSTRIAL
ASIGNATURA: MATEMÁTICAS
FECHA:
TEMA: EXPRESIONES ALGEBRAICAS
DOCENTE: FIS. MAGNO SOLÓRZANO
UNIDAD: 3
PARALELO:
NOMBRE (S) ESTUDIANTE(S):
TRABAJO AUTÓNOMO # 4
INDICACIONES GENERALES:
➢
Estimados estudiantes el trabajo autónomo tiene una duración de 10 horas y
tiene un valor de 10 puntos.
DESARROLLO DE TEMAS:
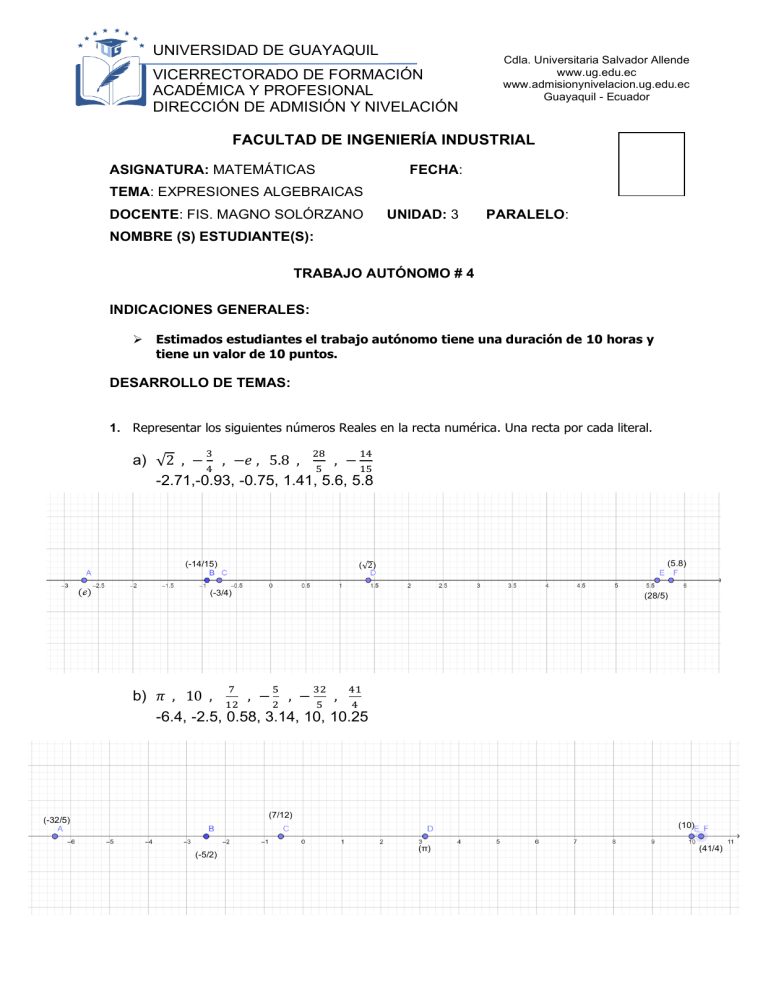
1. Representar los siguientes números Reales en la recta numérica. Una recta por cada literal.
3
28
14
a) √2 , − 4 , −𝑒 , 5.8 , 5 , − 15
-2.71,-0.93, -0.75, 1.41, 5.6, 5.8
(-14/15)
(ℯ)
(5.8)
(√2)
(-3/4)
7
(28/5)
5
32
41
b) 𝜋 , 10 , 12 , − 2 , − 5 , 4
-6.4, -2.5, 0.58, 3.14, 10, 10.25
(7/12)
(-32/5)
(10)
(-5/2)
(π)
(41/4)
UNIVERSIDAD DE GUAYAQUIL
Cdla. Universitaria Salvador Allende
www.ug.edu.ec
www.admisionynivelacion.ug.edu.ec
Guayaquil - Ecuador
VICERRECTORADO DE FORMACIÓN
ACADÉMICA Y PROFESIONAL
DIRECCIÓN DE ADMISIÓN Y NIVELACIÓN
2. Determinar la relación de orden entre los siguientes números Reales:
-24 _<__ 2
2
5
_=_
8
20
-π _<__ -3
36
5
_>_
−
37
19
6
4
_=_ 4
3
4
-35 _>_ -40
3. Un carpintero quiere cortar una plancha de madera de 256 cm de largo y 96 cm de ancho en
cuadrados lo más grandes posibles.
a) ¿Cuál debe ser la longitud del lado de cada cuadrado?
Descomponiendo en sus factores primos:
256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 2⁸
96 = 2 × 2 × 2 × 2 × 2 × 3 = 2⁵ × 3
𝒎𝒄𝒅 (𝟐𝟓𝟔, 𝟗𝟔) = 𝟐⁵ = 𝟑𝟐 𝒄𝒎 será la longitud del lado del cuadrado.
b) ¿Cuántos cuadrados se obtienen de la plancha de madera?
𝟐𝟓𝟔 ÷ 𝟑𝟐 = 𝟖 𝒄𝒖𝒂𝒅𝒓𝒂𝒅𝒐𝒔 𝒆𝒏𝒕𝒓𝒂𝒓á𝒏 𝒆𝒏 𝒆𝒍 𝒍𝒂𝒓𝒈𝒐 𝒅𝒆𝒍 𝒕𝒂𝒃𝒍ó𝒏
𝟗𝟔 ÷ 𝟑𝟐 = 𝟑 𝒄𝒖𝒂𝒅𝒓𝒂𝒅𝒐𝒔 𝒆𝒏𝒕𝒓𝒂𝒓á𝒏 𝒆𝒏 𝒆𝒍 𝒂𝒏𝒄𝒉𝒐 𝒅𝒆𝒍 𝒕𝒂𝒃𝒍ó𝒏.
𝟖𝒙𝟑 = 𝟐𝟒 𝒔𝒆 𝒐𝒃𝒕𝒆𝒏𝒅𝒓á𝒏 𝟐𝟒 𝒄𝒖𝒂𝒅𝒓𝒂𝒅𝒐𝒔
4. Teresa tiene un reloj que da una señal cada 60 minutos, otro reloj que da una señal cada
150 minutos y un tercero que da una señal cada 360 minutos. A las 10 de la mañana los tres
relojes han coincidido en dar la señal. ¿A qué hora volverán a dar la señal otra vez juntos?
60 150 360 | 2
30 75 180 | 2
15 75 90 | 2
15 75 45 | 3
5 25 15 | 3
5 25
5 |5
1 5
1 |5
1 1
1
𝑚. 𝑐. 𝑚. (60,150,360) = 2𝑥2𝑥2𝑥3𝑥3𝑥5𝑥5 = 1800
1800/60 = 30 ℎ𝑜𝑟𝑎𝑠
Respuesta: Si coincidieron a las 10 de la mañana y deben pasar 30 horas para que lo hagan
nuevamente eso significa que debe pasar un día y 6 horas más para que coincidan, es decir que
darán la señal juntos a las 4 de la tarde del día siguiente.
5. Cristina tiene cubos verdes de 15 cm de lado y cubos naranjas de 25 cm de lado. Apilando
los cubos en dos columnas, una de cubos verdes y otra de cubos naranjas, quiere conseguir
que las dos columnas sean iguales. Determine el número de cubos, como mínimo, que
necesita de cada color.
15 25 | 3
5 25 | 5
1 5 |5
1 |
𝑚. 𝑐. 𝑚. (15, 25) = 3𝑥5𝑥5 = 75𝑐𝑚
Respuesta: Para que las dos columnas sean iguales de cada color se necesitan:
5 𝑐𝑢𝑏𝑜𝑠 𝑑𝑒 15 𝑐𝑚
3 𝑐𝑢𝑏𝑜𝑠 𝑑𝑒 25 𝑐𝑚
UNIVERSIDAD DE GUAYAQUIL
VICERRECTORADO DE FORMACIÓN
ACADÉMICA Y PROFESIONAL
DIRECCIÓN DE ADMISIÓN Y NIVELACIÓN
Cdla. Universitaria Salvador Allende
www.ug.edu.ec
www.admisionynivelacion.ug.edu.ec
Guayaquil - Ecuador
6. Roberto tiene una pista de carreras con dos autos. El primer auto le da una vuelta completa
a la pista en 33 segundos y el segundo auto en 17 segundos. Julio también tiene una pista
con dos autos: el primero da la vuelta completa en 36 segundos y el segundo lo hace en 42
segundos. Ambos llegan a un acuerdo donde el ganador será aquel que tenga en su pista los
dos autos situados en la meta al mismo tiempo. ¿Quién ganará?
Roberto
33 | 3
11 | 11
1 |
33=3x11
17=17
mcm(33,17)= 3x11x17=561
Julio
36 | 2
42 | 2
18 | 2
21 | 3
9 |3
7 |7
3 |3
1 |
1 |
36=2x2x3x3
42=2x3x7
mcm(36,42)= 2x2x3x3x7 252
Respuesta: El ganador será Julio puesto que sus autos se encontrarán en menor
tiempo que los autos de Roberto
7. Miguel quiere pintar su casa, y según sus cálculos necesitará 12 litros de pintura blanca, 24
litros de pintura celeste y 16 litros de pintura café. Pero quiere comprar los tarros de pintura
de modo que tengan la misma cantidad de litros y que el número de tarros sea el menor
posible. Determine de cuántos litros debe ser cada tarro y cuántos va a necesitar de cada
color.
El M.C.D (12, 24, 16)= 22 = 4.
La cantidad de litros de cada tarro de pintura será de 4 litros.
Pintura blanca: 12/4= 3 tarros.
Pintura celeste: 24/4= 6 tarros
Pintura café: 16/4= 4 tarros
8. Los estudiantes de un paralelo de nivelación pueden formar grupos para los talleres de 3, 5
y 6 estudiantes, sin que sobre o falte ninguno. ¿Cuántos estudiantes habrá en ese paralelo,
si su número está comprendido entre 45 y 65?
5=5
6= 2x3
MCD(3,5,6)= 2x3x5=30
Numero = 30 * 2 = 60 estudiantes
6|2
3|3
1|
9. Resolver las siguientes operaciones matemáticas:
−2 + 5 − {27 − 2[−4 − 24 − 5] + 14 − 8(3)} + 10
−2 + 5 − {27 + 8 + 48 + 10 + 14 − 24} + 10
UNIVERSIDAD DE GUAYAQUIL
VICERRECTORADO DE FORMACIÓN
ACADÉMICA Y PROFESIONAL
DIRECCIÓN DE ADMISIÓN Y NIVELACIÓN
Cdla. Universitaria Salvador Allende
www.ug.edu.ec
www.admisionynivelacion.ug.edu.ec
Guayaquil - Ecuador
−2 + 5 − 27 − 8 − 48 − 10 − 14 − 24 + 10
−109 + 39 = −70
3
4
− {4−2 − 5 + 8 − [2 + 𝑥32 + (−5)] + 16 + 24}
5
5
3
4
− {4−2 − 5 + 8 − [2 + 𝑥9 − 5] + 16 + 24}
5
5
3
36
− {4−2 − 5 + 8 − [2 +
− 5] + 16 + 24}
5
5
3
36
− {4−2 − 5 + 8 − [−3 + ] + 16 + 24}
5
5
3
21
− {4−2 − 5 + 8 −
+ 16 + 24}
5
5
3
21
− {4−2 + 43 − }
5
5
3
1 194
}
−{ +
5
16
5
3 3109 −3061
−
=
5
80
80
3 1
27 − √8 + 4
2−
3
2𝑥
2
10 −
5
1
27 − 2 + 4
2−
3
2𝑥 48
5
1
31 − 2
2−
5
2𝑥 16
61
2− 2
5
8
244
234
2−
=−
5
5
UNIVERSIDAD DE GUAYAQUIL
VICERRECTORADO DE FORMACIÓN
ACADÉMICA Y PROFESIONAL
DIRECCIÓN DE ADMISIÓN Y NIVELACIÓN
10.
0.65 ÷ 6.5 + 9.9
6 1
21
24
(5 × 36 + 4.8 − 16) × 169
0.1 + 9.9
1 1 24 21
24
(5 × 6 + 5 − 16) × 169
10
1 24 21
24
(30 + 5 − 16) × 169
10
169 24
48 × 169
10
= 20
1
2
4
4
50
3 (6 − ) + 6 ( ) − ( )
3
3
3
18 − 4
24 50
3(
)+
−
3
3
3
14
24 50
3( )+
−
3
3
3
42 24 50
+
−
3
3
3
42 + 24 − 50 16
=
3
3
54 5
+
−
+ 3 3
2
3
8
1+ 1 1+ 1
9+3
2
2
54 5
+
3
2
−
+ 3 3
1
1
8
1+4 1+6 9+3
3
2
Cdla. Universitaria Salvador Allende
www.ug.edu.ec
www.admisionynivelacion.ug.edu.ec
Guayaquil - Ecuador
UNIVERSIDAD DE GUAYAQUIL
VICERRECTORADO DE FORMACIÓN
ACADÉMICA Y PROFESIONAL
DIRECCIÓN DE ADMISIÓN Y NIVELACIÓN
Cdla. Universitaria Salvador Allende
www.ug.edu.ec
www.admisionynivelacion.ug.edu.ec
Guayaquil - Ecuador
59
3
2
3
−
+
4+1 6+1
27 + 8
9+ 3
4
6
59
3 2
− + 3
5 7
35
4 6 9+ 3
59
5
7
3
−
+
12 12 27 + 35
3
59
5
7
−
+ 3
12 12 62
3
5
7 59 155 − 217 + 354 292 146 73
−
+
=
=
=
=
12 12 62
372
372 186 62
11. Simplifique las siguientes expresiones algebraicas de modo que no queden signos de
agrupación:
1
3
3
2
3
1
3
𝑥 + 𝑦 {5𝑥 − 𝑦 + 6 [− 𝑥 + 𝑥𝑦 − 6𝑦 + 𝑥𝑦 + 𝑥 + 7𝑥𝑦] − 6𝑥}
2
4
2
9
4
2
4
1
3
3
19
33
𝑥 + 𝑦 {5𝑥 − 𝑦 + 6 [ 𝑥 + 𝑥𝑦 − 6𝑦] − 6𝑥}
2
4
2
36
4
1
3
3
19
99
𝑥 + 𝑦 {5𝑥 − 𝑦 + 𝑥 +
𝑥𝑦 − 36𝑦 − 6𝑥}
2
4
2
6
2
1
3 13
75 99
𝑥 + 𝑦{ 𝑥 −
+ 𝑥𝑦}
2
4
6
2
2
1
13
225 2 75 297 2
𝑥 + 𝑥𝑦 −
𝑦 +
+
𝑥𝑦
2
8
8
2
8
4𝑐 − {𝑐 2 − 4[2𝑐𝑑 + 𝑐𝑑 2 − 4𝑑 2 + 𝑐 2 𝑑 + 4𝑐 2 + 6] + 2𝑑[3𝑐 + 4𝑑 − 1 − 6] + 𝑑 }
4𝑐 − {𝑐 2 − 8𝑐𝑑 − 4𝑐𝑑 2 + 16𝑑 2 − 4𝑐 2 𝑑 − 16𝑐 2 − 24 + 2𝑑[3𝑐 + 4𝑑 − 7] + 𝑑 }
4𝑐 − {𝑐 2 − 8𝑐𝑑 − 4𝑐𝑑 2 + 16𝑑 2 − 4𝑐 2 𝑑 − 16𝑐 2 − 24 + 6𝑐𝑑 + 8𝑑 2 − 14𝑑 + 𝑑 }
4𝑐 − {−15𝑐 − 2𝑐𝑑 − 4𝑐𝑑 2 + 24𝑑 2 − 4𝑐 2 𝑑 + 24𝑑 2 − 4𝑐 2 𝑑 − 24 − 13𝑑 }
4𝑐 + 15𝑐 2 + 2𝑐𝑑 + 4𝑐 2 𝑑 + 24𝑑 2 + 4𝑐 2 𝑑 + 24 + 13𝑑
12. Realizar las siguientes operaciones entre polinomios:
5𝑚4 − 3𝑚𝑛 − 7𝑚2 + 6𝑚2 − 7𝑚4 − 5 − (11𝑚2 + 12𝑚𝑛 − 9)
5𝑚4 − 3𝑚𝑛 − 7𝑚2 + 6𝑚2 − 7𝑚4 − 5 − 11𝑚2 − 12𝑚𝑛 + 9)
−2𝑚4 − 15𝑚𝑛 − 12𝑚2 + 4
UNIVERSIDAD DE GUAYAQUIL
VICERRECTORADO DE FORMACIÓN
ACADÉMICA Y PROFESIONAL
DIRECCIÓN DE ADMISIÓN Y NIVELACIÓN
Cdla. Universitaria Salvador Allende
www.ug.edu.ec
www.admisionynivelacion.ug.edu.ec
Guayaquil - Ecuador
(
6𝑝3 − 28𝑝𝑟 4 − 1𝑟 2
15𝑝2 𝑟 2 − 36𝑝𝑟 4 + 32
12 − 3𝑟 2 + 60𝑝3
)−(
)+(
)
8
48
10
(
180𝑝3 − 840𝑝𝑟 4 − 30𝑟 2 − 75𝑝2 𝑟 2 + 180𝑝𝑟 4 − 160 + 288 − 72𝑟 2 + 1440𝑝3
)
240
(
−660𝑝𝑟 4 + 1620𝑝3 − 102𝑟 2 − 75𝑝2 𝑟 2 + 128
)
240