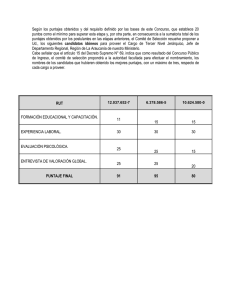
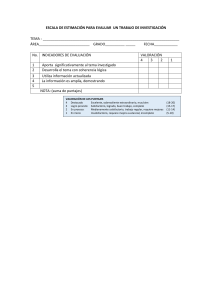
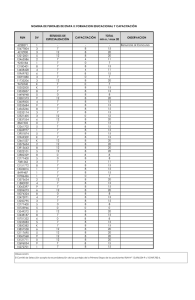
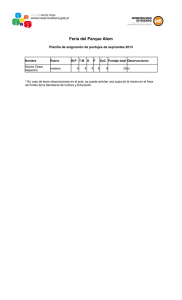
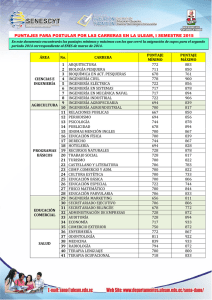
ESTADÍSTICA INFERENCIAL EN PSICOLOGÍA Tarea 4: Ejercicios de puntajes z y curva normal Nombre: __________________ Fecha: __________ Núm. de lista: ______ 1. ¿Para qué tipo de variables es posible obtener puntajes z? 2. ¿Cuál es el propósito primordial de los puntajes estandarizados? ¿Por qué podríamos preferir trabajar con puntajes z en lugar de puntajes brutos? 3. ¿Qué proporción de una distribución normal cae debajo de…? z = -1.32? ___________________ z = 0.35? ___________________ 4. Para todos los ejercicios siguientes, dibuja la curva normal y señala la ubicación de los puntajes brutos y de los puntajes z. 5. En una distribución normal que incluye a 100 personas, con = 15 y s = 3, ¿cuántas personas caen debajo de los siguientes puntajes? X = 19: _____________________ X = 13: _____________________ 6. ¿Qué puntajes z corta el 50% central de la curva normal? ¿A qué percentiles corresponden? 7. Si se aplica un examen a 200 niños y se obtiene una = 12 y una s = 4, ¿cuál es el rango probable para este grupo? ¿Qué porcentaje del grupo se espera que este incluido dentro de este rango? 8. Si una distribución normal tiene una = 10 y una s = 2, ¿cuál es el puntaje que una persona debe obtener para estar incluida en el 40% inferior? (Usar el valor de z más cercano). ¿Cuál sería su percentil? 9. Si sólo se puede elegir a 200 de 400 solicitantes para un curso especial de entrenamiento, y la distribución tiene una = 70 y una s = 5, ¿cuál es el puntaje a partir del cual se decidiría qué solicitantes serían aceptados? 10. Se aplicó un examen de Certificación de Psicología a 150 psicólogos. La prueba presentó una distribución normal, con una media de 100 y una desviación estándar de 20. a) Miriam obtuvo una puntuación de 110. ¿Cuál fue su puntaje z y en qué percentil se ubicó? b) Rodrigo sacó 90 puntos. ¿Cuántas personas quedaron por debajo de él? c) Por encima de Elisa hubo 50 personas de las 150 examinadas. ¿Cuántos puntos obtuvo en el examen? 11. Obtén los puntajes z de dos de las personas cuyos datos recolectaste en la tarea anterior (incluye la sustitución en la fórmula de z) e indica qué porcentaje de participantes se encuentran por debajo de ambos puntajes. 12. Plantea un ejercicio de percentiles y resuélvelo.