CINEMÁTICA

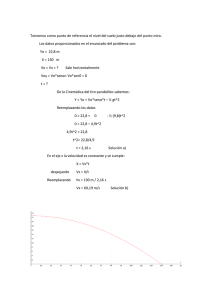
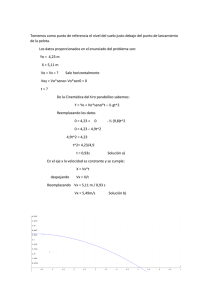
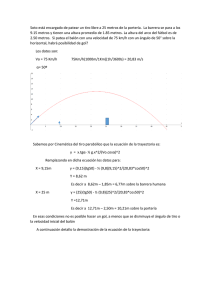
CINEMÁTICA
1.- Cae una piedra desde lo alto de la pared Norte del Eiger. Observamos que en atravesar
un escalón vertical de 6m, en el cual nos encontramos, tarda una décima de segundo. ¿Qué
distancia nos queda para llegar a la cima desde lo alto del escalón? Sol: 183.4m
En la segunda parte la piedra recorre 6m en 0,1s, con una velocidad
inicial v0 que es la que tiene al llegar al escalón:
6 = v0t + ½ gt2,, v0t= 6 - ½ gt2,, v0 = 6 - ½ gt2 / t
v0 = 6 – 4,9·0,12 / 0,1 = 59,51 m/s
La primera parte es un movimiento de caída libre con v0 = 0
por tanto la velocidad con que llega al escalón es: v = gt,, t = v / g
t = 59,51m/s / 9,8 m/s2 = 6,072s
La altura recorrida en ese tiempo será: h = v0t + ½ gt2 = ½ gt2
h = 4,9 · 6,0722 = 180,67m
Nota: la solución que dan es incorrecta, para obtenerla han tenido que considerar que en la
segunda parte el movimiento es uniforme y v = 6 / 0,1 = 60m/s
2. Dos aviones se cruzan (a distinta altura) perpendicularmente con velocidades de 800
km/h ¿Cuál es la velocidad de uno respecto al otro antes y después de cruzarse?
La velocidad relativa del avión a con respecto al
avión b es la suma vectorial de
y
:
ab =
y su módulo será:
=
=
= 1131,37 Km/h
3. Un aeroplano vuela sobre el mar, horizontalmente, a una altura de 1000m y con una
velocidad de 200 km/h. Su misión es abastecer de provisiones a un barco que se desplaza
en la misma dirección a 20 km/h. (a) Demuestra que el avión debe dejar caer las provisiones cuando se encuentre a 715m del barco (distancia horizontal). (b) Resuelve el mismo
problema en el caso en el cual el barco se está moviendo en la dirección opuesta. Sol.(b)
837,2 m
Colocamos el origen de coordenadas al nivel del mar, justo bajo el avión en el momento de
dejar caer las provisiones. Las ecuaciones de movimiento serían
Para el avión:
xp = v · t = (200·1000/3600) · t = 55,555 m/s ·t
yp = h - ½ g·t2 = 1000 - ½ 9,8·t2
Para el barco:
xB = x0 + v·t = d + (20·1000/3600)·t = d + 5,555m/s ·t
yB = 0
(1)
(3)
Igualando las ecuaciones (1) y (2):
55,555m/s ·t = d + 5,555m/s ·t
Igualando las ecuaciones (3) y (4):
1000 - ½ 9,8·t2 = 0
(2)
(4)
(5)
De esta última, despejamos t:
y sustituimos en (5):
d = (55,555m/s – 5,555m/s)·14,3s = 715m
Si el barco se mueve en dirección contraria:
Para el avión queda igual: xP = 55,555m/s ·t
Para el barco: xB = d – 5,555m/s ·t
Igualando estas dos: d = (55,555m/s + 5,555m/s)·14,3s = 873,8m
4. La gravedad de la Luna es 6 veces menor que en la Tierra. Discute cómo influye esta
diferencia es la altura y el alcance de un tiro parabólico. Sol: 6 veces más en la Luna.
Las ecuaciones de un tiro parabólico son:
x = v0 cosα · t
vx = v0 cosα
2
y = v0 senα · t - ½ g’ t
vy = v0 senα – g’·t ,, donde g’ es la gravedad en la Luna
Cuando el proyectil llega a la máxima altura: vy = 0,, 0 = v0 senα – g’·t,, t = v0 senα /g’
y sustituyendo en la ecuación de y:
Si la gravedad en la luna (g’) es 6 veces menor que la de la tierra (g):
g’ = g / 6 y sustituimos en las ecuación anterior:
Lo mismo haríamos para el alcance. El alcance se consigue cuando el proyectil cae a
tierra, es decir y = 0.
0 = v0 senα · t - ½ g’t2,, t (v0 senα - ½ g’t) = 0
hay dos soluciones: t = 0 (antes del disparo) y
Como g’ = g / 6, sustituimos:
5. Carlos i son his mountain bike, approaching a creek that is 7m wide. A ramp with an
incline of 10º has been built for daring people who try to jump the creek. Carlos is
traveling at his bike’s maximum speed, 40 km/h. (a) Should Carlos attempt to jump or
emphatically hit the brakes?. (b) What is the minimum speed a bike must have to make this
jump?. Sol; (a) Apply brakes! (b) 51 km/h.
El movimiento que realiza la bicicleta es
análogo a un tiro parabólico y por tanto se
puede descomponer en:
- Un movimiento horizontal uniforme: x = v0 cosα · t
- Un movimiento vertical uniformemente acelerado: y = v0 senα · t - ½ g t2
v0 = 40 km/h = 40 x 1000 / 3600 = 11,111 m/s
Cuando llegue al suelo al otro lado: y = 0, sustituyendo:
0 = v0 senα · t - ½ g t2 ,, aquí despejamos t: 0 = t (v0 senα - ½ g t),,
hay dos soluciones: t = 0
v0 senα - ½ g t = 0,, despejamos t en ésta:
y el alcance será: x = v0·t·cosα = 11,111· 0,394 · cos10º = 4,31m
No llegaría al otro lado, luego tiene que frenar con todas sus fuerzas.
Vamos a calcular ahora la velocidad mínima para lograr el salto:
Tomamos la ecuación del tiempo calculada un poco más arriba:
y la sustituimos en la ecuación del alcance:
v0= 14,162m/s = 14,162x 3600 / 1000 = 51 km/h
6. Un satélite se mueve con velocidad de módulo constante en una órbita circular muy
próxima a la superficie de la Tierra, siendo su aceleración 9,8 m/s2. Calcula: (a) el
módulo de su velocidad y (b) el tiempo que tarda en dar una revolución completa.
Se trata de un movimiento circular uniforme, luego:
Si consideramos como radio de la órbita el radio de la Tierra: R = 6,37x106m
El tiempo que tarda el satélite en dar una vuelta, es lo que se denomina período:
7. Un automóvil que marcha a 96,6 km/h tiene ruedas de 0,762m de diámetro. ¿Cuál es la
velocidad angular de las ruedas alrededor del eje? Si la rueda se detiene uniformemente
en 30 vueltas, ¿Cuál es la aceleración angular?, ¿Qué distancia recorre el automóvil
durante el periodo de frenado?
Se trata de un movimiento circular uniforme, donde v = 96,6 km/h = 26,83 m/s
para una vuelta completa: θ = 2π y además t = T (periodo), sustituyendo:
Si tarda 30 vueltas en parar de manera uniforme, el tiempo empleado en frenar será:
t = 30·T = 30· 0,0892 = 2,676 s
Desde que empieza a frenar, el movimiento es uniformemente retardado.
La velocidad angular durante el frenado es: ω = ω0 – α·t
pero cuando para totalmente: ω = 0,, luego ω0 = α · t
Si despejamos α (aceleración angular):
La aceleración tangencial será: a = R·α = 0,381 · 26,319 = 10,028 m/s2
y la distancia recorrida durante la frenada:
x = v0 t - ½ a t2 = 26,833·2,676 - ½ · 10,028 · 2,6762 = 35,9 m
8. Encuentra en función de la latitud, la velocidad y la aceleración (debidas a la rotación)
de un punto sobre la superficie terrestre. Si en Granada la latitud es λ = 37º, ¿cuál es el
valor de la velocidad y de la aceleración?. Radio de la Tierra = 6370 km, Sol: 1332 km/h
y 2,8x10-2 m/s2.
Todos los puntos sobre la superficie de la Tierra se mueven con movimiento circular
uniforme.
La latitud en Granada es el ángulo que forma el radio de la Tierra en Granada con el radio
de la Tierra en el Ecuador.
Si R es el radio del paralelo que pasa por Granada: R = r · cosλ, donde r es el radio de la
Tierra, r = 6,370x106m
Y la velocidad en Granada es tangente al paralelo y paralela al Ecuador:
v = ω · R = ω · r · cosλ
Por otra parte la velocidad angular será:
ω = 2π / T = 2π / 24 horas = 2π / 8640 s = 72,722x10-6 rad/s
Sustituyendo en la ecuación de la velocidad:
v = ω · r · cosλ = 72,722x10-6 rad/s· 6,370x106 m· cos37º = 369,96 m/s = 1332 km/h
La aceleración será:
a = ω2·R = ω2· r · cosλ = (72,722x10-6)2 · 6,370x106· cos37º = 0,0269 m/s2 =
= 2,7x10-2 m/s2