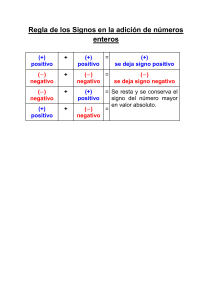
COLEGIO CAMPRESTE DE MELGAR Formando seres integrales, autónomos y felices. NOMBRE: ASIGNATURA: MATEMÁTICAS DOCENTE: INGRID LIZETH GUASCA GARNICA ÁREA: MATEMÁTICAS PERIODO: I GRADO: SEPTIMO FECHA: TALLER N° 1 FECHA ENTREGA: NÚMEROS ENTEROS Desde la era primitiva el hombre siempre buscó respuestas a sus inquietudes. La inquietud permitió la aparición de conceptos abstractos en la mente del hombre primitivo ya evolucionado. Cuando el hombre desarrolla la capacidad de darle sentido racional a las cosas, nace el concepto de cantidad. Los números negativos Los números negativos antiguamente conocidos como “números deudos” o “números absurdos”, datan de una época donde el interés central era la de convivir con los problemas cotidianos a la naturaleza. Los números negativos, además complementan o extienden el conjunto de los números naturales, generado por un defecto de los números naturales: la generalidad para la operación de resta y división. Por ejemplo 5 – 9 resulta –4, que no es natural, no se cumple entonces la propiedad de clausura o cerradura en los naturales. El hombre, visto en la imposibilidad de realizar, en general, la operación de resta crea otro conjunto, que viene hacer el conjunto de los números negativos. Los números naturales junto con los negativos formarán luego el conjunto de los números enteros; es decir los números naturales complementados con los negativos. Observemos el siguiente gráfico: Las primeras manifestaciones de su uso se remontan al siglo V, en oriente, y no llega hasta occidente hasta el siglo XVI. En oriente se manipulaban números positivos y negativos, estrictamente se utilizaba los ábacos, usando tablillas o bolas de diferentes colores. Sin embargo, los chinos no aceptaron la idea de que un número negativo pudiera ser solución de una ecuación. Corresponde a los Indios la diferenciación entre números positivos y negativos, que interpretaban como créditos y débitos, respectivamente, distinguiéndolos simbólicamente. La notación muy difundida para los números positivos y negativos fue gracias a Michael Stifel. La difusión de los símbolos germánicos (+) y (-), se popularizó con el matemático alemán Stifel (1487 – 1567) en el siglo XV, antes de ello se utilizaba la abreviatura de p para los positivos y m para los negativos. RECTA NUMÉRICA En la recta numérica podemos representar los números enteros, los negativos se ubican a la izquierda y los positivos a la derecha. Recordemos que los numeros enteros se clasifican en: Enteros positivos o Números naturales: 1,2,3,4,5,6,7,8,9,10,11… Enteros negativos: -1, -2, -3, -4, -5… Cero PLANO CARTESIANO Hasta fines del siglo XVIII los números negativos no eran aceptados universalmente. Gerolamo Cardano, en el siglo XVI, llamaba a los números negativos “falsos”, pero en su Ars Magna (1545) los estudió exhaustivamente. John Wallis (1616 - 1703), en su Aritmética Infinito (1655), “demuestra” la imposibilidad de su existencia diciendo que “esos entes tendrían que ser a la vez mayores que el infinito y menores que cero”. Leonardo Euler es el primero en darles estatuto legal, en su Anteitung Zur Algebra (1770) trata de “demostrar” que (1).(-1) = +1; argumentaba que el producto tiene que ser +1 ó -1 y que, sabiendo que se cumple (1).(-1)=-1, tendrá que ser: (-1).(-1) = +1. El plano cartesiano está formado por dos rectas numéricas perpendiculares, una horizontal y otra vertical que se cortan en un punto. La recta horizontal es llamada eje de las abscisas o de las equis (x), y la vertical, eje de las ordenadas o de las yes, (y); el punto donde se cortan recibe el nombre de origen. El plano cartesiano tiene como finalidad describir la posición de puntos, los cuales se representan por sus coordenadas o pares ordenados. Las coordenadas se forman asociando un valor del eje de las equis a uno de las yes, respectivamente, esto indica que un punto (P) se puede ubicar en el plano cartesiano tomando como base sus coordenadas, lo cual se representa como: P (x, y) COLEGIO CAMPRESTE DE MELGAR Formando seres integrales, autónomos y felices. Para localizar puntos en el plano cartesiano se debe llevar a cabo el siguiente procedimiento: 1. Para localizar la abscisa o valor de x, se cuentan las unidades correspondientes hacia la derecha si son positivas o hacia la izquierda si son negativas, a partir del punto de origen, en este caso el cero. 2. Desde donde se localiza el valor de x, se cuentan las unidades correspondientes (en el eje de las ordenadas) hacia arriba si son positivas o hacia abajo, si son negativas y de esta forma se localiza cualquier punto dadas ambas coordenadas. DOCENTE: INGRID LIZETH GUASCA GARNICA ÁREA: MATEMÁTICAS PERIODO: I GRADO: SEPTIMO Opuesto aditivo o inverso aditivo: (+6) + (-6) = 0 (+104) + (-104) = 0 Todo número entero adicionado con su opuesto aditivo da como resultado cero. PROPIEDADES DE LA RESTA DE NÚMEROS ENTEROS Clausurativa o Interna: a − b Pertenece enteros 10 − (−5) Pertenece enteros No es Conmutativa: a-b≠ b-a 5−2≠2−5 MULTIPLICACIÓN DE NÚMEROS ENTEROS La multiplicación de varios números enteros es otro número entero, que tiene como valor absoluto el producto de los valores absolutos y, como signo, el que se obtiene de la aplicación de la regla de los signos. Regla de los signos PROPIEDADES DE LA MULTIPLICACIÓN DE NÚMEROS ENTEROS Clausurativa o Interna: VALOR ABSOLUTO DE UN NÚMERO ENTERO El valor absoluto de un número entero es el número natural que resulta al suprimir su signo. |−a| = a |a| = a Ejm: |-5| = 5 |13| = 13 PROPIEDADES DE LA SUMA DE NÚMEROS ENTEROS Clausurativa o interna: (-8) + (-19) = -27 (+47) + (-18) = +29 La suma obtenida al adicionar números enteros es un número entero. Conmutativa: a+b=b+a (-67) + (+89) = +22 (+89) + (-67) = +22 En toda adición el orden de los sumandos no altera la suma. Asociativa: (-14) + (+24) + (-5) (-14 + 24) -5 = -14 + (+24 -5) (+10) -5 = -14 + (+19) +5 = +5 Al asociar dos o más sumandos de una adición, en distinto orden, la suma no se altera. Modulativa o de elemento neutro: 0 + (-41) = (-41) (+27) + 0 = (+27) La adición de un número entero con cero da como resultado el mismo número entero. a·b 2 · (−5) Asociativa: (a · b) · c = a · (b · c) (2 · 3) · (−5) = 2· [(3 · (−5)] 6 · (−5) = 2 · (−15) -30 = -30 Conmutativa: a·b=b·a 2 · (−5) = (−5) · 2 -10 = -10 Elemento neutro: todo número entero multiplicado por 1 da el mismo número entero a ·1 = a (−5)· 1 = (−5) Distributiva: a · (b + c) = a · b + a · c (−2)· (3 + 5) = (−2) · 3 + (−2) · 5 (−2)· 8 =- 6 - 10 -16 = -16 Sacar factor común: a · b + a · c = a · (b + c) (−2) · 3 + (−2) · 5 = (−2) · (3 + 5) DIVISIÓN DE NÚMEROS ENTEROS La división de dos números enteros es igual al valor absoluto del cociente de los valores absolutos entre el dividendo y el divisor, y tiene de signo, el que se obtiene de la aplicación de la regla de los signos. COLEGIO CAMPRESTE DE MELGAR Formando seres integrales, autónomos y felices. DOCENTE: INGRID LIZETH GUASCA GARNICA ÁREA: MATEMÁTICAS PERIODO: I GRADO: SEPTIMO PROPIEDADES DE LA DIVISIÓN DE NÚMEROS ENTEROS 9. No es una operación interna: 10. En la cuenta corriente del banco tenemos $1250. Se paga el recibo de la luz, que vale $83; el recibo del teléfono, que vale $37, y dos cheques de gasolina de $40 cada uno. ¿Cuánto dinero queda en la cuenta corriente? (−2) : 6 No es Conmutativa: a/b ≠ b/a 6 / (−2) ≠ (−2)/6 1. EJERCICIOS Realiza un resumen de la historia por medio de una historieta. 2. Realiza un mapa conceptual de las propiedades de números enteros. 3. Dibuja una recta numérica y representa los siguientes números enteros usando colores, luego ordénalos de mayor a menor: +8, −9, +5, 0, −1, +6, −7, +11, −6. 4. En una ciudad en un día de otoño el termómetro varió entre las siguientes temperaturas: Máxima: +3 °C. Mínima: −4 °C. a) Representa ambos valores en una recta numérica. b) Indica sí pudieron marcarse estas temperaturas ese día en la ciudad, si alguna no se pudo presentar indica cual es: −2 °C, +4 °C, −5 °C, +1 °C, 0 °C, +2 °C. c) Representa las temperaturas indicadas anteriormente en una recta numérica. 5. 6. Pitágoras nació el año 585 a.C y murió el año 495 a.C ¿Cuántos años vivió Pitágoras? 11. Compramos un refrigerador. Cuando lo enchufamos a la red eléctrica está a la temperatura ambiente, que es de 25 °C. Si cada hora baja la temperatura 5 °C, ¿a qué temperatura estará al cabo de 6 horas? 12. Un día de invierno amaneció a 3 grados bajo cero. A las doce del mediodía la temperatura había subido 8 grados, y hasta las cuatro de la tarde subió 2 grados más. Desde las cuatro hasta las doce de la noche bajó 4 grados, y desde las doce a las 6 de la mañana bajó 5 grados más. ¿Qué temperatura hacía a esa hora? 13. Ubica en el plano cartesiano los siguientes puntos: P(-4,6) Q(-8,-6) R(0,-3) S(-5,0) T(0,7) U(5,6) V(4,-5) 14. Coloca V o F a cada una de las siguientes frases. Justifica en caso de que la respuesta sea falsa: Realiza las siguientes operaciones con números enteros: -5 + 3 + 5 – 13 = (-4) + 5 –(3) – 10 = 5-6-15+8-9 = (3-8) - (10-15) = 23 – 18 +30 –(2-4) = 3(4-3) + 6 = 5(-3+5-6+9-10) – 3(3-10) = (-12+21) - (4-10) = Como representarías las siguientes situaciones con números enteros: Juan le debe 56 pesos a María. Un submarino desciende 100 metros en el océano Felipe asciende 100m por encima del mar La temperatura en Rusia baja 15 grados por debajo de 0°. Pitágoras nació en el año 585 años a.C. 7. En una estación de esquí la temperatura más alta ha sido de -2°C, y la más baja, de -23°C. ¿Cuál ha sido la diferencia de temperatura? 8. Un avión vuela a 11000 m y un submarino está a -850 m. ¿Cuál es la diferencia de altura entre ambos? Al eje de las x se le conoce como eje de las ordenas ( ) Al eje y se se conoce como origen Si sumamos dos números negativos el resultado será negativo ( ) Si multiplicamos dos números positivos el resultado será positivo ( ) La división cumple con la propiedad conmutativa ( ) Al dividir dos números enteros el resultado siempre será un numero entero ( ) La resta es conmutativa ya que a-b es igual a b-a ( ) Los números negativos fueron aceptamos desde un inicio por las personas ( ) Antes de usar el signo menos (-) se usaba la letra m para representar los números negativos ( ) “Ars magna” fue una obra de Jhon Wallis ( )