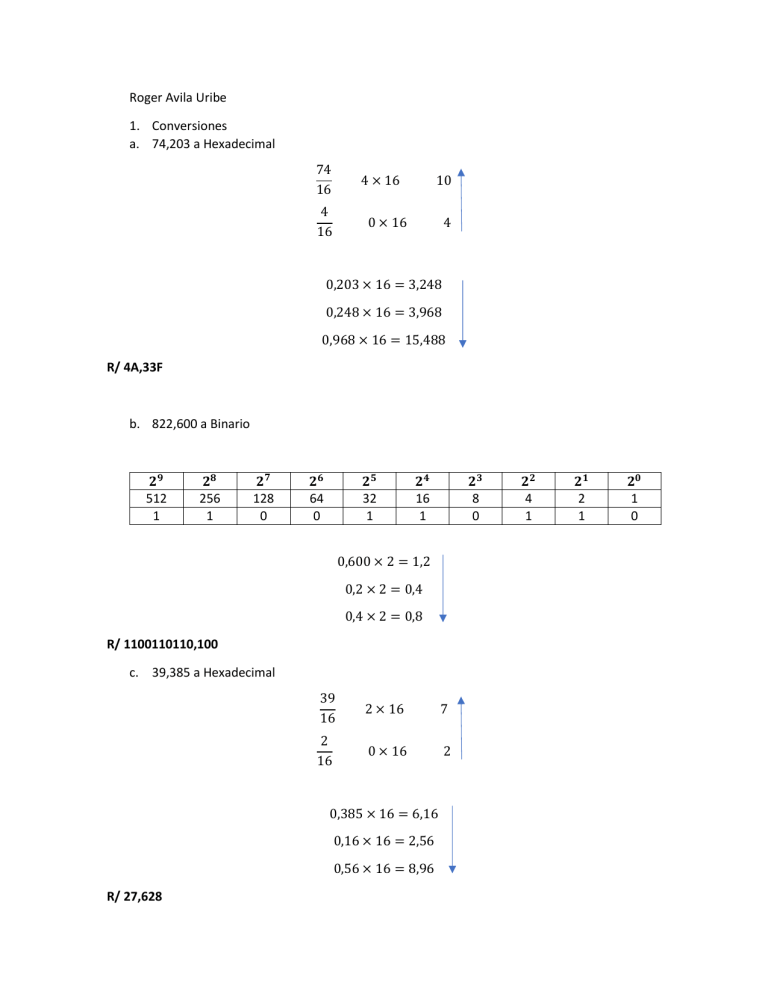
Roger Avila Uribe 1. Conversiones a. 74,203 a Hexadecimal 74 16 4 × 16 4 16 10 0 × 16 4 0,203 × 16 = 3,248 0,248 × 16 = 3,968 0,968 × 16 = 15,488 R/ 4A,33F b. 822,600 a Binario 𝟐𝟗 512 1 𝟐𝟖 256 1 𝟐𝟕 128 0 𝟐𝟔 64 0 𝟐𝟓 32 1 𝟐𝟒 16 1 𝟐𝟑 8 0 0,600 × 2 = 1,2 0,2 × 2 = 0,4 0,4 × 2 = 0,8 R/ 1100110110,100 c. 39,385 a Hexadecimal 39 16 2 × 16 7 2 16 0 × 16 2 0,385 × 16 = 6,16 0,16 × 16 = 2,56 0,56 × 16 = 8,96 R/ 27,628 𝟐𝟐 4 1 𝟐𝟏 2 1 𝟐𝟎 1 0 d. 128,111 a Binario 𝟐𝟕 128 1 𝟐𝟔 64 0 𝟐𝟓 32 0 𝟐𝟒 16 0 𝟐𝟑 8 0 𝟐𝟐 4 0 𝟐𝟏 2 0 𝟐𝟎 1 0 0,111 × 2 = 0,222 0,222 × 2 = 0,444 0,444 × 2 = 0,888 R/ 10000000,000 2. Convierta los siguientes números a complemento a 2 con el número bits indicados a. -12 con 6 bits 𝟐𝟓 32 0 𝟐𝟒 16 0 𝟐𝟑 8 1 𝟐𝟐 4 1 𝟐𝟏 2 0 𝟐𝟎 1 0 𝟐𝟏 2 1 𝟐𝟎 1 0 𝟐𝟐 4 0 𝟐𝟏 2 1 110100 R/ 𝑪𝟐 (−𝟏𝟐𝟏𝟎 ) = 𝟏𝟏𝟎𝟏𝟎𝟎𝟐 b. -30 con 6 bits 𝟐𝟓 32 0 𝟐𝟒 16 1 𝟐𝟑 8 1 𝟐𝟐 4 1 100010 R/ 𝑪𝟐 (−𝟑𝟎𝟏𝟎 ) = 𝟏𝟎𝟎𝟎𝟏𝟎𝟐 c. -98 con 8 bits 𝟐𝟕 128 0 𝟐𝟔 64 1 𝟐𝟓 32 1 𝟐𝟒 16 0 𝟐𝟑 8 0 10011110 R/ 𝑪𝟐 (−𝟗𝟖𝟏𝟎 ) = 𝟏𝟎𝟎𝟏𝟏𝟏𝟏𝟎𝟐 𝟐𝟎 1 0 d. -27 con 6 bits 𝟐𝟓 32 0 𝟐𝟒 16 1 𝟐𝟑 8 1 𝟐𝟐 4 0 𝟐𝟏 2 1 𝟐𝟎 1 1 100101 R/ 𝑪𝟐 (−𝟐𝟕𝟏𝟎 ) = 𝟏𝟎𝟎𝟏𝟎𝟏𝟐 3. Sea la siguiente función Boolea (Secciones 2.3 y 2.4 del libro de Muñoz): a. Utilizando mapas de Karnaught encuentre la mínima expresión Suma de Productos. b. Utilizando mapas de Karnaught encuentre la mínima expresión Producto de Sumas. c. Implemente en VHDL ambas expresiones usando el software EDAPLAYGROUND. En el informe debe incluir una impresión de pantalla de la descripción en VHDL y la simulación. d. Construir el esquemático de la función simplificada para la suma de productos. ̅ + 𝐴𝐶𝐷 + 𝐴𝐵̅𝐶 𝐹 = 𝐴𝐵𝐶̅ + 𝐵̅𝐶̅ 𝐷











