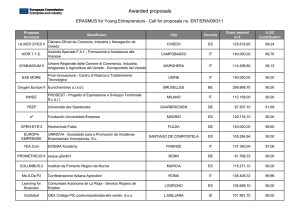
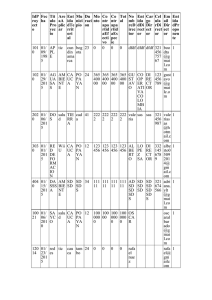
1 BO15-003.xmcd ABB AB Rapport Report R BO15-003 Från - From Reg Datum - Date Sida - Page 1/26 Författare - Author PPHB/BOD Ulf Åkesson Godkännare - Approv ed by Ordernr - Ref.No. 2015-02-09 X Utredning, teoretisk undersökning -Analysis, theoretical investigation X Slutrapport Final report Tom my Borg Antal textsidor - No of text pages LTB145D1 Load combinations 24 Antal bilagor - No of supplements 2 Breaker type: LTB72,5D1 3-pole FSA Dim ension print: 1HSBDG00001-329 Zone: 0.5 g according to IEEE 693 2005 ________________________________________________________________________________ Sammanfattning - Summary Load com binations calculation is carried out according to IEC 62155 and IEEE 693 2005. TThe circuit breaker is equipped with porcelain insulators and ηsupport fram e. LC1: Design pressure 100%, Mass 100%, Normal wind 30%, Static term inal load 100% and Impact at operation 100%. Extrem e load cases: LC2: Design Pressure 100%, Mass 100%, Ice load 100%, Norm al wind 110%, Static terminal load 100% and Impact at operation 100%. LC3: Design Pressure 100%, Mass 100%, High wind 100%, Static terminal load 100% and Impact at operation 100%. LC4: Design Pressure 100%, Mass 100%, Short circuit load 100%, Normal wind 100%, Static term inal load 100% and Im pact at operation 100%. LC5: Design Pressure 100%, Mass 100%, Earthquake load 100%, Norm al wind 10%, Static terminal load 100 % and Impact at operation 100 %. Basic loads: Horizontal earthquake acceleration 0.5 g Static term inal loads according to IEC Short circuit current Ice 40 kA 20 mm Norm al wind High wind 34 m/s 46 m/s Maximum bending moment on the post insulator occurs under short circuit condition and maximum bending moment on the support frame occurs under earthquake condition: Calculated Minim um Safety factor Allowed IEEE 693 2005 bending moment failing load Calculated For com bined loads Nm Nm M 1 3 3 Breaking chamber M5x = 3.8 ´ 10 M = 11.0 ´ 10 = 2.9 SE = 2.0 1 1 1 M5x 2732 2118-BL 1 M 2 3 3 = 2 Post insulator M4y = 10.0 ´ 10 M = 20.0 ´ 10 SS = 2.0 M4y 2 2 2 2 1HSB422732-G M 3 3 3 Support fram e M5x = 39.2 ´ 10 M = 100.0 ´ 10 = 2.6 SE = 1.5 3 3 3 M5x 1HSB425422-VP 3 Maximum foundation load occurs under earthquake condition: Bending mom ent Nm Foundation Transversal forces Direction x N 3 M5x = 39.2 ´ 10 3 3 T5x = 12.8 ´ 10 3 Vertical f orce N Direction y N 3 T5y = 12.1 ´ 10 Result: The breaker is well suited to withstand above specified combined loads. 3 3 T5z = 21.3 ´ 10 3 2 BO15-003.xmcd Content: 1 Introduction 2 Specification of equipment 3 Individual mechanical loads 3.1 Dead weight 3.2 Dead weight from ice load on conductor 3.3 Dead weight from ice load on breaker 3.4 Design pressure according to IEC 62155 3.5 Normal wind load on equipm ent 3.6 High wind load on equipm ent 3.7 Normal wind load on conductor without ice 3.8 Normal wind load on ice loaded conductor 3.9 High wind load on conductor 3.10 Static terminal load 3.11 Im pact load due to operation 3.12 Short circuit load transversal to conductor 3.13 Earthquake load 4 Load combinations 5 Summary of calculated loads 6 Calculation of safety factors for insulators and support frame 7 Foundation load 8 Foundation bolts Appendix 1 - Dimension print 1HSBDG00001-329 Appendix 2 - General dimensions used in calculation 3 BO15-003.xmcd 1 Introduction Load com binations calculation is carried out according to: IEC 62155 and IEEE 693 2005. The different m echanical loads on the circuit-breaker are individually calculated and after that combined into actual load combinations. The following load combinations are considered. Norm al load case: LC1: Design pressure 100%, Mass 100%, Normal wind 30%, Static term inal load 100% and Impact at operation 100%. Extrem e load cases: LC2: Design Pressure 100%, Mass 100%, Ice load 100%, Norm al wind 110%, Static terminal load 100% and Impact at operation 100%. LC3: Design Pressure 100%, Mass 100%, High wind 100%, Static terminal load 100% and Impact at operation 100%. LC4: Design Pressure 100%, Mass 100%, Short circuit load 100%, Normal wind 100%, Static term inal load 50% and Im pact at operation 100%. LC5: Design Pressure 100%, Mass 100%, Earthquake load 100%, Norm al wind 10%, Static terminal load 70% and im pact at operation 100%. Specified mechanical loads: v = 34 m /s Norm al wind vh = 46 m /s High wind t = 20 mm Ice thickness Fthy = 750 N Static horizontal terminal load transversal to line Fthx = 1250 N Static horizontal terminal load along line Ftz = 1000 N Static vertical terminal load Fyimp = 1000 N Horizontal load at operation Fzimp = 12000 N Vertical load at operation Isc = 40 kA Short circuit current ahr = 16.00 m /s2 Horizontal earthquake acceleration Based on 0.5 g horizontal acceleration and damping of critical dam ping ζ=0.02. 2 Specification of equipment. Circuit-breaker of type: Dim ension print: LTB72,5D1 3-pole operated with FSA mechanism 1HSBDG00001-329 See appendix 1 and 2. 4 BO15-003.xmcd 3 Individual mechanical loads 3.1 Dead weight m = 138 kgs 1 Breaking unit m = 112 kgs 1 Post insulator m = 177 kgs Link gear m = 170 kgs Operating mechanism m = 160 kgs 1 Support frame 1 2 3 4 5 Total dead weight affecting one support frame 2 mtot := å i=1 æ mi × 3 ö ç ÷+ è 2 ø 2 mtot = 7.1 ´ 10 4 m å i i=3 kgs +m 5 2 Total dead weight Centre of gravities according to appendix 2. h = 4.499 m Height to centre of gravity of breaking unit h = 3.117 m Height to centre of gravity of post isolator h = 2.298 m Height to centre of gravity of link gear h = 1.702 m Height to centre of gravity of operating mechanism h = 1.103 m Height to centre of gravity of support fram e 1 2 3 4 5 3.2 Dead weight from ice load on conductor according to IEC 62271-1 Lc = 1.3 m Length of conductor bound to equipment Dc = 100 mm Diameter of conductor t = 20 mm Thickness of ice N/m Ice load Qicez := QI× Lc× 2 N Ice load on terminals Qicez = 646.9 N Vertical load from ice on term inal of one breaker pole QI := π× éë( Dc + t) - Dc ùû × 10 2 2 -6 × 900× t 5 BO15-003.xmcd 3.3 Dead weight from ice load on breaker according to IEC 62271-1 Extra weight in kgs due to ice: mice = i = i 1 23.2 Ice on one breaking unit 2 24.1 Ice on one post insulator 3 33.4 Ice on pole beam 4 50.5 5 67.7 Ice on operating m echanism Ice on one support fram e 3.4 Design Pressure according to IEC 62155 5 Pdes = 7 ´ 10 Pa Design pressure p = 1 2 Breaking cham ber insulator Post insulator Ds = p m Sealing diam eter m Outer diam eter m Inner diameter 0.200 0.160 Do = p 0.225 0.190 Di = p 0.175 0.130 Mdes := Pdes × p π 32 ( p) × Ds (× Dop)2 + (Dip)2 2 Do p Mdes = 993 Nm Equivalent bending moment on breaking chamber insulator due to design pressure Mdes = 491 Nm Equivalent bending moment on post insulator due to design pressure 1 2 6 BO15-003.xmcd 3.5 Normal wind load on equipment v = 34 m /s cc := 0.9 Drag factor, cyli ndrical surface cp := 1.3 Drag factor, flat surf ace A = 0.40 m2 Frontal area of breaking unit A = 0.33 m2 Frontal area of post insulator A = 0.77 m2 Frontal area of link gear A = 0.58 m2 Frontal area of operating mechanism A = 0.37 m2 Frontal area of support fram e B = 0.41 m2 Side area of breaking unit B = 0.33 m2 Side area of post insulator B = 0.10 m2 Side area of link gear B = 0.48 m2 Side area of operating mechanism B = 0.49 m2 Side area of support fram e 1 2 3 4 5 1 2 3 4 5 Norm al wind speed Load due to normal wind [X direction]: 2 Qwx := 0.625× v × A × cc 1 1 2 Qwx := 0.625× v × A × cc 2 2 2 Qwx := 0.625× v × A × cp 3 3 2 Qwx := 0.625× v × A × cp 4 4 2 Qwx := 0.625× v × A × cp 5 5 Qwx = 262 N Load in X direction on one breaking unit due to normal wind Qwx = 217 N Load in X direction on one post insulator due to normal wind Qwx = 723 N Load in X direction on link gear due to normal wind Qwx = 545 N Load in X direction on operating mechanism due to normal wind Qwx = 348 N Load in X direction on one support fram e due to normal wind 1 2 3 4 5 7 BO15-003.xmcd Load due to normal wind [Y direction]: 2 Qwy := 0.625× v × B × cc 1 1 2 Qwy := 0.625× v × B × cc 2 2 2 Qwy := 0.625× v × B × cp 3 3 2 Qwy := 0.625× v × B × cp 4 4 2 Qwy := 0.625× v × B × cp 5 5 Qwy = 267 N Load in Y direction on one breaking unit due to normal wind Qwy = 217 N Load in Y direction on one post insulator due to normal wind Qwy = 94 N Load in Y direction on link gear due to norm al wind Qwy = 451 N Load in Y direction on operating mechanism due to normal wind Qwy = 460 N Load in Y direction on one support fram e due to norm al wind 1 2 3 4 5 Heights to locations where loads on the equipm ent will be calculated L = 5.204 m Height to upper terminal L = 3.837 m Height to bottom of breaking unit L = 2.417 m Height to bottom of post insulator 0 1 2 8 BO15-003.xmcd Bending mom ent due to normal wind [X direction]: ( 1 1) Mwx := Qwx × (h - L ) + Qwx × ( h - L ) 2 1 1 2 2 2 2 Mwx := Qwx × h - L 1 1 2 Mwx := 3 å i=1 æ Qwx × h × 3 ö + ç i i 2÷ è ø 4 å i=3 æ Qwxi × hi ö ç ÷ + Qwx5× h5 è 2 ø Mwx = 173 Nm Bending mom ent in X direction on one breaking unit due to normal wind Mwx = 697 Nm Bending mom ent in X direction on one post insulator due to normal wind Mwx = 4460 Nm Bending mom ent in X direction on one support fram e due to normal wind 1 2 3 Bending mom ent due to normal wind [Y direction]: ( 1 1) Mwy := Qwy × (h - L ) + Qwy × ( h - L ) 2 1 1 2 2 2 2 Mwy := Qwy × h - L 1 1 2 Mwy := 3 å i=1 æ Qwy × h × 3 ö + ç i i 2÷ è ø 4 å i=3 æ Qwyi × hi ö ç ÷ + Qwy5× h5 è 2 ø Mwy = 177 Nm Bending mom ent in Y direction on one breaking unit due to normal wind Mwy = 707 Nm Bending mom ent in Y direction on one post insulator due to normal wind Mwy = 3813 Nm Bending mom ent in Y direction on one support f ram e due to normal wind 1 2 3 9 BO15-003.xmcd 3.6 High wind load on equipment Load due to high wind [X direction]: 2 Qwhx := 0.625× vh × A × cc 1 1 2 Qwhx := 0.625× vh × A × cc 2 2 2 Qwhx := 0.625× vh × A × cp 3 3 2 Qwhx := 0.625× vh × A × cp 4 4 2 Qwhx := 0.625× vh × A × cp 5 5 Qwhx = 479 N Load in X direction on one breaking unit due to high wind Qwhx = 397 N Load in X direction on one post insulator due to high wind Qwhx = 1324 N Load in X direction on link gear due to high wind Qwhx = 997 N Load in X direction on operating mechanism due to high wind Qwhx = 636 N Load in X direction on one support fram e due to high wind 1 2 3 4 5 Load due to high wind [Y direction]: 2 Qwhy := 0.625× vh × B × cc 1 1 2 Qwhy := 0.625× vh × B × cc 2 2 2 Qwhy := 0.625× vh × B × cc 3 3 2 Qwhy := 0.625× vh × B × cp 4 4 2 Qwhy := 0.625× vh × B × cp 5 5 Qwhy = 488 N Load in Y direction on one breaking unit due to high wind Qwhy = 397 N Load in Y direction on one post insulator due to high wind Qwhy = 119 N Load in Y direction on link gear due to high wind Qwhy = 825 N Load in Y direction on operating mechanism due to high wind Qwhy = 842 N Load in Y direction on one support fram e due to high wind 1 2 3 4 5 10 BO15-003.xmcd Heights to locations where loads on the equipm ent will be calculated L = 5.204 m Height to upper terminal L = 3.837 m Height to bottom of breaking unit L = 2.417 m Height to bottom of post insulator 0 1 2 Bending mom ent due to high wind [X direction]: ( 1 1) Mwhx := Qwhx × ( h - L ) + Qwhx × ( h - L ) 2 1 1 2 2 2 2 Mwhx := Qwhx × h - L 1 1 2 Mwhx := 3 å i=1 æ Qwhx × h × 3 ö + ç 1 i 2÷ è ø 4 å i=3 æ Qwhxi × hi ö ç ÷ + Qwhx5× h5 è 2 ø Mwhx = 317 Nm Bending mom ent in X direction on one breaking unit due to high wind Mwhx = 1276 Nm Bending mom ent in X direction on one post insulator due to high wind Mwhx = 8547 Nm Bending mom ent in X direction on one support fram e due to high wind 1 2 3 Bending mom ent due to high wind [Y direction]: ( 1 1) Mwhy := Qwhy × ( h - L ) + Qwhy × (h - L ) 2 1 1 2 2 2 2 Mwhy := Qwhy × h - L 1 1 2 Mwhy := 3 å i=1 æ Qwhy × h × 3 ö + ç i i 2÷ è ø 4 å i=3 æ Qwhyi × hi ö ç ÷ + Qwhy5× h5 è 2 ø Mwhy = 323.1 Nm Bending mom ent in Y direction on one breaking unit due to high wind Mwhy = 1294 Nm Bending mom ent in Y direction on one post insulator due to high wind Mwhy = 6920 Nm Bending mom ent in Y direction on one support f ram e due to high wind 1 2 3 11 BO15-003.xmcd 3.7 Normal wind load on conductor without ice v = 34 m /s cc = 0.9 Drag factor, cyli ndrical surface Norm al wind Ac := Lc× Dc× 0.001× 2 Ac = 0.3 m2 Frontal area of conductor Transversal load due to normal wind on c onductor: 2 Qwno := .625× v × cc × Ac Qwno = 169.1 N Norm al wind load on conductor per term inal Bending mom ent due to normal wind from on conductor: ( 1 1) 2 Mwno := Qwno× (h - L ) 2 1 2 Mwno := Qwno× h - L × 1 1 Mwno := Qwno× h × 3 3 1 2 Mwno = 56 Nm Bending mom ent in Y direction on one breaking unit due to normal wind on conductor Mwno = 352 Nm Bending mom ent in Y direction on one post insulator due to normal wind on conductor Mwno = 1141 Nm Bending mom ent in Y direction on one support f ram e due to normal wind on conductor 1 2 3 12 BO15-003.xmcd 3.8 Normal wind load on ice loaded conductor v = 34 m /s cc = 0.9 Drag factor, cyli ndrical surface Norm al wind Ac := Lc× ( Dc× 0.001 + t× 0.001) × 2 Ac = 0.3 m2 Frontal area of conductor Transversal load due to normal wind on iced conductor: 2 Qwice := .625× v × cc× Ac N Norm al wind load on iced conductor Qwice = 202.9 Bending mom ent due to normal wind from iced conductor: ( 1 1) 2 Mwice := Qwice× ( h - L ) 2 1 2 Mwice := Qwice× h - L × 1 1 Mwice := Qwice× h × 3 3 1 2 Mwice = 67.2 Nm Bending mom ent in Y direction on one breaking unit due to normal wind on conductor with ice Mwice = 422 Nm Bending mom ent in Y direction on one post insulator due to normal wind on conductor with ice Mwice = 1369 Nm Bending mom ent in Y direction on one support f ram e due to normal wind on conductor with ice 1 2 3 13 BO15-003.xmcd 3.9 High wind load on conductor At high wind it is considered that no ice loading exists. vh = 46 m /s cc = 0.9 Drag factor, cyli ndrical surface High wind Ach := Lc× Dc× 0.001× 2 Ach = 0.3 m2 Frontal area of conductor Transversal load due to high wind on c onductor: 2 Qwhno := .625× vh × cc × Ach N High wind load on conductor Qwhno = 309.5 Bending mom ent due to high wind on conductor: ( 1 1) 2 Mwhno := Qwhno× ( h - L ) 2 1 2 Mwhno := Qwhno× h - L × 1 1 Mwhno := Qwhno× h × 3 3 1 2 Mwhno = 102 Nm Bending mom ent in Y direction on one breaking unit due to high wind on conductor Mwhno = 644 Nm Bending mom ent in Y direction on one post insulator due to high wind on conductor Mwhno = 2088 Nm Bending mom ent in Y direction on one support fram e due to high wind on conductor 1 2 3 14 BO15-003.xmcd 3.10 Static terminal load according to IEC 62271-100 The static terminal load due to weight and type of connection will be added to all load cases. Static term inal load due to wind and ice are separately calculated in other paragraphs. Fthy = 750 N Horizontal load transversal to line Fthx = 1250 N Horizontal load along line Ftz = 1000 N Vertical load Lb = 0.255 m Distance from centre line to end of terminal flange Bending mom ent along line due to static term inal load: ( 0 1) + Ftz× Lb MFthx := Fthx× (L - L ) + Ftz× Lb 2 0 2 3 MFthx := ( Fthx× L + Ftz× Lb) × 3 0 2 MFthx := Fthx× L - L 1 MFthx = 1964 Nm Bending mom ent in X direction on one breaking unit due to static terminal load MFthx = 3739 Nm Bending mom ent in X direction on one post insulator due to static terminal load Nm Bending mom ent in X direction on one support fram e due to static terminal load 1 2 3 MFthx = 10.140 ´ 10 3 Bending mom ent transversal to line due to static terminal load: ( 0 1) MFthy := Fthy× ( L - L ) 2 0 2 MFthy := Fthy× L - L 1 MFthy := Fthy× L × 3 3 0 2 MFthy = 1025 Nm Bending mom ent in Y direction on one breaking unit due to static terminal load MFthy = 2090 Nm Bending mom ent in Y direction on one post insulator due to static terminal load MFthy = 5855 Nm Bending mom ent in Y direction on one support fram e due to static terminal load 1 2 3 15 BO15-003.xmcd 3.11 Im pact load due to operation The bending mom ent at the support frame and bottom of post insulator due to operational impact is added to all load com binations. Fyimp = 1000 N Horizontal force at operation Fzimp = 12000 N Vertical f orce at operat ion Mimp = 1500 Nm Bending mom ent on structure at operation 3.12 Short circuit load transversal to conductor The electromagnetic force between interrupters is calculated by the following formula: K := 2.95 Engineering factor Isc = 40 kArms Max. three phase fault current Lph = 1.500 m Spacing between phases a := 1 Support factor ( Lsc := L - L 0 1 ) + Lb×2 + Lc×2 m Interrupter length and part of conductor length 2 Fscy := 0.2 × K× Isc Lph × a× Lsc N Electromagnetic force on equipm ent Fscy = 2818 Bending mom ent due to short circuit: hsc = 4.5 m Height to centre of conductor under short circuit ( 1) Mscy := Fscy× (hsc - L ) 2 2 Mscy := Fscy× hsc - L 1 Mscy = 1865 Nm Bending mom ent in X direction on one breaking unit due to short circuit load Mscy = 5866 Nm Bending mom ent in X direction on one post insulator due to short circuit load 1 2 16 BO15-003.xmcd 3.13 Earthquake load fnatural = 2.8 Hz Fundamental m ode ζ = 0.02 Damping of critical dam ping ah = 5.0 m /s2 Horizontal acceleration av = 2.5 m /s2 Vertical acceleration ahr = 16.00 m /s2 Horizontal acceleration response avr = 8.00 m /s2 Vertical acceleration response Load on each mass due to horizontal earthquake acceleration: Feh := ahr × m i i Load on each mass due to vertical earthquake acceleration: Fev := avr × m i i Bending mom ent due to earthquake acceleration: (1 1 (1 2 Meh := Feh × h - L 1 1 ) Meh := Feh × h - L ) + Feh2×(h2 - L2) 2 4 2 Meh := 3 1 å i=1 æ Feh × h × 3 ö + ç i i 2÷ è ø å i=3 æ Fehi × hi ö ç ÷ + Feh5× h5 è 2 ø Meh = 1462 Nm Bending mom ent on one breaking unit due to horizontal earthquake acceleration Meh = 5851 Nm Bending mom ent in on one post insulator due to horizontal earthquake acceleration Nm Bending mom ent in on one support fram e due to horizontal earthquake acceleration 1 2 3 Meh = 31.672 ´ 10 3 17 BO15-003.xmcd 4 Load combinations LC1 (see definition clause1): Horizontal loads [X direction]: T1x := Qwx × 0.3 + Fthx 1 1 T1x := T1x + Qwx × 0.3 2 1 2 Qwx + Qwx ö 3 æ 3 4 T1x := T1x × + ç + Qwx ÷ × 0.3 3 2 2 5 2 è ø Horizontal loads [Y direction]: ( ) T1y := Qwy + Qwno × 0.3 + Fthy 1 1 T1y := T1y + Qwy × 0.3 2 1 T1y := T1y × 3 2 3 2 2 + æ Qwy + Qwy 3 ç è 4 ö + Qwy ÷ × 0.3 + Fyimp ø 5 2 Bending moment [X direction]: M1x := Mdes + Mwx × 0.3 + MFthx 1 1 1 1 M1x := Mdes + Mwx × 0.3 + MFthx 2 2 2 2 M1x := Mwx × 0.3 + MFthx 3 3 3 Bending moment [Y direction]: ( 1 ( 2 ) 1 ) 2 M1y := Mdes + Mwy + Mwno × 0.3 + MFthy 1 1 1 M1y := Mdes + Mwy + Mwno × 0.3 + MFthy + Mimp 2 2 ( 2 ) M1y := Mwy + Mwno × 0.3 + MFthy + Mimp 3 3 3 3 Vertical loads [Z direction]: T1z := m × 9.81 + Ftz 1 1 T1z := T1z + m × 9.81 2 1 T1z := T1z × 3 2 3 2 2 4 + å i=3 æ mi × 9.81 ö ç ÷ + m5× 9.81 + Fzimp è 2 ø 18 BO15-003.xmcd LC2 (see definition clause1): Horizontal loads [X direction]: T2x := Qwx × 1.1 + Fthx 1 1 T2x := T2x + Qwx × 1.1 2 1 2 T2x := T2x × 3 3 + 2 2 æ Qwx + Qwx 3 ç è ö 4 + Qwx ÷ × 1.1 ø 5 2 Horizontal loads [Y direction]: ( ) T2y := Qwy + Qwice × 1.1 + Fthy 1 1 T2y := T2y + Qwy × 1.1 2 1 2 Qwy + Qwy ö 3 æ 3 4 T2y := T2y × + ç + Qwy ÷ × 1.1 + Fyimp 3 2 2 5 2 è ø Bending moment [X direction]: M2x := Mdes + Mwx × 1.1 + MFthx 1 1 1 1 M2x := Mdes + Mwx × 1.1 + MFthx 2 2 2 2 M2x := Mwx × 1.1 + MFthx 3 3 3 Bending moment [Y direction]: ( 1 ( 2 ) 1 ) 2 M2y := Mdes + Mwy + Mwice × 1.1 + MFthy 1 1 1 M2y := Mdes + Mwy + Mwice × 1.1 + MFthy + Mimp 2 2 ( 2 ) M2y := Mwy + Mwice × 1.1 + MFthy + Mimp 3 3 3 3 Vertical loads [Z direction]: ( ) T2z := m + mice × 9.81 + Qicez + Ftz 1 1 1 ( ) T2z := T2z + m + mice × 9.81 2 1 T2z := T2z × 3 3 2 2 2 2 4 + å i=3 é ( mi + micei ) × 9.81ù ê ú + ( m5 + mice5) × 9.81 + Fzimp 2 ë û 19 BO15-003.xmcd LC3 (see definition clause1): Horizontal loads [X direction]: T3x := Qwhx + Fthx 1 1 T3x := T3x + Qwhx 2 1 T3x := T3x × 3 3 2 2 2 Qwhx + Qwhx 3 + 4 + Qwhx 2 5 Horizontal loads [Y direction]: T3y := Qwhy + Qwhno + Fthy 1 1 T3y := T3y + Qwhy 2 1 T3y := T3y × 3 2 Qwhy + Qwhy 3 3 + 2 2 4 + Qwhy + Fyimp 5 2 Bending moment [X direction]: M3x := Mdes + Mwhx + MFthx 1 1 1 M3x := Mdes + Mwhx + MFthx 2 2 2 1 2 M3x := Mwhx + MFthx 3 3 3 Bending moment [Y direction]: M3y := Mdes + Mwhy + Mwhno + MFthy 1 1 1 1 1 M3y := Mdes + Mwhy + Mwhno + MFthy + Mimp 2 2 2 2 2 M3y := Mwhy + Mwhno + MFthy + Mimp 3 3 3 3 Vertical loads [Z direction]: T3z := m × 9.81 + Ftz 1 1 T3z := T3z + m × 9.81 2 1 T3z := T3z × 3 2 3 2 2 4 + å i=3 æ mi × 9.81 ö ç ÷ + m5× 9.81 + Fzimp è 2 ø 20 BO15-003.xmcd LC4 (see definition clause1): Horizontal loads [X direction]: T4x := Qwx + Fthx× 0.5 1 1 T4x := T4x + Qwx 2 1 2 T4x := T4x × 3 3 2 2 Qwx + Qwx 3 + 4 + Qwx 5 2 Horizontal loads [Y direction]: T4y := Qwy + Qwno + Fthy× 0.5 + Fscy 1 1 T4y := T4y + Qwy 2 1 T4y := T4y × 3 2 3 2 2 Qwy + Qwy 3 + 4 2 + Qwy + Fyimp 5 Bending moment [X direction]: M4x := Mdes + Mwx + MFthx × 0.5 1 1 1 1 M4x := Mdes + Mwx + MFthx × 0.5 2 2 2 2 M4x := Mwx + MFthx × 0.5 3 3 3 Bending moment [Y direction]: M4y := Mdes + Mwy + Mwno + MFthy × 0.5 + Mscy 1 1 1 1 1 1 M4y := Mdes + Mwy + Mwno + MFthy × 0.5 + Mscy + Mimp 2 2 2 2 2 M4y := Mwy + Mwno + MFthy × 0.5 + Mimp 3 3 3 3 Vertical loads [Z direction]: T4z := m × 9.81 + Ftz× 0.5 1 1 T4z := T4z + m × 9.81 2 1 T4z := T4z × 3 2 3 2 2 4 + å i=3 æ mi × 9.81 ö ç ÷ + m5× 9.81 + Fzimp è 2 ø 2 21 BO15-003.xmcd LC5 (see definition clause1): Horizontal loads [X direction]: T5x := Qwx × 0.1 + Fthx× 0.7 + Feh 1 1 1 T5x := T5x + Qwx × 0.1 + Feh 2 1 2 T5x := T5x × 3 3 2 2 2 æ Qwxi × 0.1 ö ç ÷ + Qwx5× 0.1 + è 2 ø 4 å + i=3 4 å i=3 Feh i + Feh 5 2 Horizontal loads [Y direction]: ( ) T5y := Qwy + Qwno × 0.1 + Fthy× 0.7 + Feh 1 1 1 T5y := T5y + Qwy × 0.1 + Feh 2 1 2 2 4 Qwy é 2 æ Qwyi × 3 ö ù i ê ç ÷ T5y := + + Qwy + Qwnoú × 0.1 + Fthy× 0.7 ... 3 5 2 ê ú è 2 ø i=3 ëi = 1 û å å é 2 + ê ê ëi = 1 å æ Fehi × 3 ö ç ÷+ è 2 ø 2 ù 2 + Feh ú + Fyimp 5ú 2 û 4 Feh å i i= 3 Bending moment [X direction]: M5x := Mdes + Mwx × 0.1 + MFthx × 0.7 + Meh 1 1 1 1 M5x := Mdes + Mwx × 0.1 + MFthx × 0.7 + Meh 2 2 2 2 M5x := Mwx × 0.1 + MFthx × 0.7 + Meh 3 3 3 1 2 3 Bending moment [Y direction]: ( 1 ( 2 ) 1 ) 2 M5y := Mdes + Mwy + Mwno × 0.1 + MFthy × 0.7 + Meh 1 1 1 M5y := Mdes + Mwy + Mwno × 0.1 + MFthy × 0.7 + 2 2 ( 2 ) M5y := Mwy + Mwno × 0.1 + MFthy × 0.7 + 3 3 3 3 1 (Meh2)2 + Mimp2 (Meh3)2 + Mimp2 Vertical loads [Z direction]: T5z := m × 9.81 + Ftz× 0.7 + Fev 1 1 1 T5z := T5z + m × 9.81 + Fev 2 T5z := 3 1 é 2 ê ê ëi = 1 å 2 æ mi × 3 ö ç ÷+ è 2 ø 2 4 å i=3 ù æ mi ö ç ÷ + m5ú × 9.81 + Ftz× 3 × 0.7 ... 2 ú è2 ø û 2 4 Fev é 2 æ Fevi × 3 ö ù i 2 ê ç ÷ + + + Fev ú + Fzimp 5 2 ê ú è 2 ø i=3 ëi = 1 û å å 22 BO15-003.xmcd 5 Summary of calculated loads Horizontal loads [N]: X Norm al wind T1x = k= k k := 1 , 2 .. 3 Ice T2x = k High wind Short circuit Earthquake T3x = T4x = T5x = k k k 1 1.3·103 1.5·103 1.7·103 886.9 3.1·103 2 1.4·103 1.8·103 2.1·103 1.1·103 4.9·103 3 2.4·103 3.7·103 5.0·103 2.6·103 12.8·103 Ice High wind Short circuit Earthquake T3y = T4y = T5y = Y Norm al wind T1y = k= k T2y = k k k k 1 880.7 1.3·103 1.5·103 3.6·103 2.8·103 2 945.8 1.5·103 1.9·103 3.8·103 4.6·103 3 2.6·103 4.1·103 5.2·103 7.5·103 12.1·103 Ice High wind Short circuit Earthquake M3x = M4x = M5x = Bending moment [Nm]: X Norm al wind M1x = k= k M2x = k k k k 1 3.0·103 3.1·103 3.3·103 2.1·103 3.8·103 2 4.4·103 5.0·103 5.5·103 3.1·103 9.0·103 3 11.5·103 15.0·103 18.7·103 9.5·103 39.2·103 Ice High wind Short circuit Earthquake M3y = M4y = M5y = Y Norm al wind M1y = k= k M2y = k k k k 1 2.1·103 2.3·103 2.4·103 3.6·103 3.2·103 2 4.4·103 5.3·103 6.0·103 10.0·103 8.1·103 3 8.8·103 13.1·103 16.4·103 9.4·103 36.3·103 Ice High wind Short circuit Earthquake T3z = T4z = T5z = Vertical loads [N]: Z Norm al wind T1z = k= k T2z = k k k k 1 2.4·103 3.2·103 2.4·103 1.9·103 3.2·103 2 3.5·103 4.6·103 3.5·103 3.0·103 5.2·103 3 20.5·103 23.2·103 20.5·103 19.7·103 21.3·103 23 BO15-003.xmcd 6 Calculation of safety factors for insulators and support frame Minim um failing loads for insulators and support fram e: 3 M = 11.0 ´ 10 1 3 M = 20.0 ´ 10 2 3 M = 100.0 ´ 10 3 Nm Minim um value of breaking cham ber insulator and top of post insulator Nm Post insulator 1HSB422732-G Nm Support fram e 1HSB425422-VP Allowed safety factors according to IEC 62155 IEEE 693 2005 Safety factors direction x: Norm al wind M M k M1x k= Ice = k High wind M k M2x = k Shortcircuit M k M3x = k Earthquake M k M4x = k k M5x = 3.7 3.5 3.4 5.1 2.9 2 4.5 4.0 3.6 6.5 2.2 3 8.7 6.6 5.4 10.5 2.6 Ice SN := 2.1 2.1 1.5 k k 1 Norm al wind Safety factors direction y: High wind Short circuit Earth quake SI := SH := SS := SE := 1.2 1.2 1.2 1.2 1.2 1.2 2.0 2.0 1.5 2.0 2.0 1.5 k k k k Allowed safety factors according to IEC 62155 IEEE 693 2005 Norm al wind M M k M1y k= k 1 Ice = High wind M k M2y k = Shortcircuit M k M3y k 5.3 4.8 4.5 2 4.5 3.8 3 11.3 7.7 = Earthquake M k M4y k = k M5y k 3.1 3.4 3.3 2.0 2.5 6.1 10.7 2.8 = Norm al wind Ice SN := 2.1 2.1 1.5 k High wind Shortcircuit Earth quake SI := SH := SS := SE := 1.2 1.2 1.2 1.2 1.2 1.2 2.0 2.0 1.5 2.0 2.0 1.5 k k k k 24 BO15-003.xmcd 7 Support frame foundation loads Vertical Horizontal direction z [N] direction x [N] 3 3 LC1 T1z = 20.5 ´ 10 T1x = 2.4 ´ 10 3 3 3 3 3 3 3 3 3 3 M3y = 16.4 ´ 10 3 3 3 M4x = 9.5 ´ 10 M4y = 9.4 ´ 10 3 3 3 3 T5y = 12.1 ´ 10 3 3 3 3 T5x = 12.8 ´ 10 3 3 M2y = 13.1 ´ 10 M3x = 18.7 ´ 10 T4y = 7.5 ´ 10 3 LC5 T5z = 21.3 ´ 10 3 3 3 3 3 3 T4x = 2.6 ´ 10 3 3 M1y = 8.8 ´ 10 M2x = 15.0 ´ 10 T3y = 5.2 ´ 10 3 LC4 T4z = 19.7 ´ 10 3 3 3 Horizontal direction y [Nm] 3 3 T3x = 5.0 ´ 10 3 M1x = 11.5 ´ 10 T2y = 4.1 ´ 10 3 LC3 T3z = 20.5 ´ 10 3 3 T2x = 3.7 ´ 10 3 Horizontal direction x [Nm] T1y = 2.6 ´ 10 3 LC2 T2z = 23.2 ´ 10 Horizontal direction y [N] 3 M5x = 39.2 ´ 10 3 M5y = 36.3 ´ 10 3 3 8 Foundation bolts. Maximum load on support frame foundation bolts: Tz := Tx := Ty := Mx := My := T1z T1x T1y M1x M1y T2z T2x T2y M2x T3z T3x T3y M3x T4z T4x T4y M4x T5z T5x T5y M5x i i 3 i 3 3 3 3 3 3 3 3 3 3 3 i 3 3 3 3 i 3 M2y 3 3 M3y 3 3 M4y 3 3 M5y 3 3 Axial load and stress for M24 bolts; Load case 1 to 4: Axial stress [N/m m 2] Axial loads [N] Tz Faz := i i 4 ( max Mx , My + i 2× db i ) Faz σz := i i 352.490 Shear stress X [N/mm 2] Tx τx := i σz = i Ty i π 4 Faz = Shear stress Y [N/m m 2] × 21.185 τy := τx = i i 2 4 i 55.2 69.8 6.8 10.6 7.5 11.5 28.5·103 16.8·103 80.8 14.1 14.8 47.8 7.5 N 154.2 N/m m 2 36.4 21.3 N/m m 2 Equivalent stress: σe := i × 21.185 τy = i 19.5·103 24.6·103 54.3·103 i π (σzi)2 + 3×éë(τxi)2 + (τyi )2ùû match( max( σe) , σe) = ( 5 ) Load case that yields the highest load on foundation bolts max( σe) = 176.8 N/m m 2 For size M24 foundation bolts a material with yield point larger than se shall be used. 34.2 N/m m 2 2 25 BO15-003.xmcd 26 BO15-003.xmcd