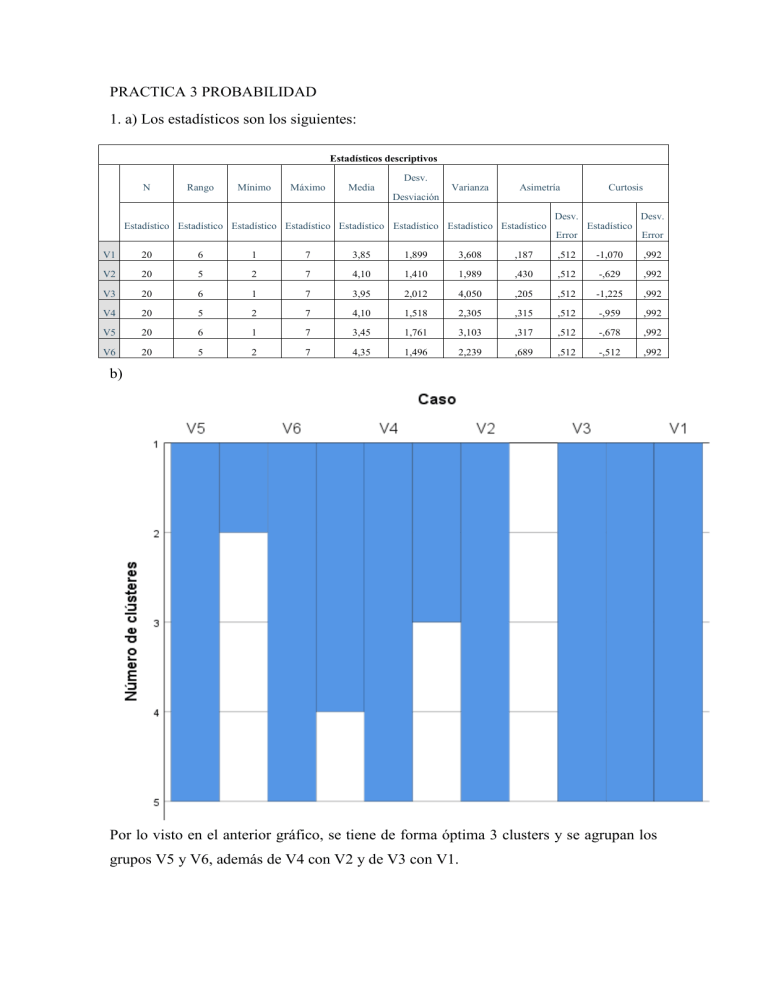
PRACTICA 3 PROBABILIDAD 1. a) Los estadísticos son los siguientes: Estadísticos descriptivos N Rango Mínimo Máximo Desv. Media Desviación Varianza Asimetría Estadístico Estadístico Estadístico Estadístico Estadístico Estadístico Estadístico Estadístico Desv. Curtosis Estadístico Error Desv. Error V1 20 6 1 7 3,85 1,899 3,608 ,187 ,512 -1,070 ,992 V2 20 5 2 7 4,10 1,410 1,989 ,430 ,512 -,629 ,992 V3 20 6 1 7 3,95 2,012 4,050 ,205 ,512 -1,225 ,992 V4 20 5 2 7 4,10 1,518 2,305 ,315 ,512 -,959 ,992 V5 20 6 1 7 3,45 1,761 3,103 ,317 ,512 -,678 ,992 V6 20 5 2 7 4,35 1,496 2,239 ,689 ,512 -,512 ,992 b) Por lo visto en el anterior gráfico, se tiene de forma óptima 3 clusters y se agrupan los grupos V5 y V6, además de V4 con V2 y de V3 con V1. c) Se incluye el dendograma a continuacion: Se observa la formación de 3 clusters o grupos para explicar las variables en este estudio. d) Por lo visto anteriormente se observa que existen 3 clusters y las agrupaciones más homogéneas ya fueron presentadas por el análisis realizado. 2. Se observa el análisis de conglomerados de la siguiente forma. Matriz de proximidades Entrada de archivo matricial Caso A B C D E F A ,000 B 58,000 C 10,000 20,000 D 40,000 2,000 10,000 ,000 5,000 E 41,000 5,000 13,000 5,000 ,000 F 50,000 52,000 40,000 50,000 25,000 ,000 G 40,000 34,000 26,000 32,000 13,000 H 34,000 20,000 16,000 18,000 I 20,000 10,000 2,000 J 34,000 8,000 G H I J 58,000 10,000 40,000 41,000 50,000 40,000 34,000 20,000 34,000 ,000 4,000 20,000 ,000 2,000 5,000 52,000 34,000 20,000 10,000 10,000 13,000 40,000 26,000 16,000 4,000 2,000 8,000 50,000 32,000 18,000 4,000 2,000 25,000 13,000 5,000 5,000 1,000 2,000 8,000 34,000 32,000 2,000 ,000 2,000 20,000 18,000 5,000 8,000 2,000 ,000 10,000 8,000 4,000 5,000 34,000 20,000 10,000 ,000 2,000 2,000 1,000 32,000 18,000 2,000 ,000 8,000 Se observa en el gráfico de casos que se tienen 8 clusters como máximo pero lo óptimo es tener 5 clusters con las variables. Como se menciona en lo anterior, en el dendograma se muestran 5 clusters donde se agrupan las variables. 3. Se realiza el análisis de conglomerados para el archivo de jóvenes de acuerdo a las instrucciones dadas, obteniendo lo siguiente. Matriz de proximidades Distancia euclídea al cuadrado Caso 1: L 2: M 3: K 4: E 5: B 6: H 7: C 8: N 9: 1: L 2: M 36,706 3: K 44,507 17,307 4: E 53,740 33,093 36,761 5: B 76,106 39,695 41,613 25,613 6: H 73,044 35,029 40,957 18,678 26,687 7: C 44,832 46,709 61,755 57,131 32,178 52,605 8: N 28,719 17,302 23,348 40,242 49,858 45,150 41,802 9: J 52,984 52,523 52,701 56,854 72,095 70,533 61,690 28,955 10: J 10: ,000 36,706 44,507 53,740 76,106 73,044 44,832 28,719 52,984 ,000 17,307 33,093 39,695 35,029 46,709 17,302 52,523 ,000 36,761 41,613 40,957 61,755 23,348 52,701 ,000 25,613 18,678 57,131 40,242 56,854 ,000 26,687 32,178 49,858 72,095 ,000 52,605 45,150 70,533 ,000 41,802 61,690 ,000 28,955 G 47,193 51,759 58,350 47,384 47,858 39,467 30,231 31,248 ,000 37,004 G 47,193 51,759 58,350 47,384 47,858 39,467 30,231 31,248 37,004 ,000 Esto es una matriz de disimilaridad. Historial de conglomeración Primera aparición del clúster de Clúster combinado Etapa Clúster 1 etapa Clúster 2 Coeficientes Clúster 1 Clúster 2 Etapa siguiente 1 2 8 17,302 0 0 3 2 4 6 18,678 0 0 4 3 2 3 23,348 1 0 6 4 4 5 26,687 2 0 8 5 7 10 30,231 0 0 8 6 1 2 44,507 0 3 7 7 1 9 52,984 6 0 9 8 4 7 57,131 4 5 9 9 1 4 76,106 7 8 0 Como se observa en el anterior análisis con las primeras instrucciones, se tiene 6 clusters, observando que es lo más lógico que se iba a formar en las agrupaciones de las variables. Con el método de Ward se tiene lo siguiente: Con el método de Ward igual se forman 6 clusters, observando que era lo más lógico que iba a pasar con las variables. 4. El análisis de clusters se realiza de la siguiente forma: Con el análisis anterior se observa que se forman 7 clusters en el análisis de la esperanza de vida de los países. Se agrupan mediante el desarrollo que tienen cada uno, estando en los clusters de más abajo los de alto desarrollo mientras que los de menor desarrollo están en los clusters de más arriba. 5. El análisis de conglomerados de estos compuestos es el siguiente: En el análisis de clusters se observa que se forman 11 clusters para que se puedan analizar los compuestos mostrados. Esto se obtiene pues hay muchas formas de hacer reaccionar los compuestos para ver que resulta. 6. El análisis es el siguiente: En ambos gráficos se observa que se forman 13 clusters para poder analizar el comportamiento de los niños, observando a la asociación esperada entre las variables que se tienen en la encuesta. 7. El análisis de vehículos es el siguiente: De acuerdo al análisis realizado se observan la conformación de 10 clusters para poder explicar las ventas de vehículos que tengan más de 100, viendo que las variables usadas se pueden agrupar de 10 formas distintas de forma óptima para ver las relaciones existentes. 8. Cuando las variables no están en la misma escala, lo que se hace es estandarizar las variables de tal forma que no tengan unidades y se pueda aplicar el análisis de conglomerados. 9. Este análisis se usa cuando se conoce o no la cantidad de clusters a usar y además sirve para muestras grandes o no y para variables cualitativas y cuantitativas. 10. La diferencia entre distancia y similaridad es que en el segundo no se tiene el axioma de la desigualdad triangular, más bien solo se tiene acotamiento o que la función aplicada sea menor o mayor que el numero arbitrario tomado. 11. Distancia euclidea, norma al cuadrado, distancia del máximo, distancia de Minkowski y la distancia de Mahalanobis. 12. Verdadero