DERIVADA PARAMÉTRICA .

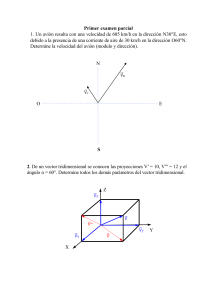
UPN, PASIÓN POR
TRANSFORMAR VIDAS
• Cálculo 1
• 2022 - 0
jiuliana.more@upn.edu.pe
SEMANA 2 – VC 01
UPN.EDU.PE
TEMARIO
Derivada Paramétrica
Tasas de cambio relacionadas
Ejemplo
Aplicaciones
Conclusiones
ONDAS DE LAGO
Se deja caer una piedra en un lago
en calma, lo que provoca ondas y
círculos. El radio r del círculo
exterior está creciendo a un ritmo
constante de 1 pies/s. Cuando el
radio es 4 pies, ¿a qué ritmo está
cambiando el área A de la región
circular perturbada?
Saberes previos
1. Derivadas
2. Regla de la cadena
Logro de Aprendizaje:
Al finalizar la sesión de aprendizaje, el
estudiante
resuelve
ejercicios
y
situaciones problemáticas usando la
derivación paramétrica y las tasas de
cambio relacionadas, siguiendo un
proceso lógico y la exactitud de su
resultado.
• DERIVADA DE UNA FUNCIÓN PARAMÉTRICA
TEOREMA:
Dadas las funciones 𝑓 y 𝑔 dos funciones derivables en un intervalo 𝐼, donde
𝑥 = 𝑓(𝑡)
ቊ
𝑦 = 𝑔(𝑡)
Además como 𝑥 e 𝑦 son funciones paramétricas, tenemos:
𝑑𝑥
= 𝑓′(𝑡)
𝑑𝑡
𝑑𝑦
= 𝑔′(𝑡)
𝑑𝑡
′
Si 𝑓 𝑡 ≠ 0,
𝑑𝑦
luego
𝑑𝑥
, estaría dada por:
𝑑𝑦 𝑔′(𝑡)
=
𝑑𝑥 𝑓′(𝑡)
Sean x e y dos funciones derivables relacionadas por la ecuación:
𝑑𝑥
Calcular dy/dt para x=1, sabiendo que 𝑑𝑡 = 2 en x=1.
Solución:
Derivamos ambos lados con respecto a t, utilizando la regla de la cadena
Cuando x= 1 y
𝑑𝑥
𝑑𝑡
= 2 , se tiene:
y = x2 + 3
• EJEMPLO:
Dada la función paramétrica, determinar
ቊ
Solución:
𝑑𝑦
𝑑𝑥
para 𝑡 = −3:
𝑥 = 3 + 𝑡3
𝑦 = 2𝑡 4 − 2𝑡 + 5
• EJEMPLO:
𝑑𝑦
Calcular la derivada 𝑑𝑥 de las funciones dadas en forma paramétrica:
a)
1
𝑥=
𝑡+1
𝑡 2
𝑦=
𝑡+1
Solución:
• b) ቊ
𝑥 = 𝑎(𝑡 − 𝑠𝑒𝑛𝑡)
𝑦 = 𝑎(1 − 𝑐𝑜𝑠𝑡)
Solución:
para 𝑡 =
𝜋
2
• EJEMPLO:
Encontrar las ecuaciones de la tangente y normal de la curva 𝑥 = 𝑡 2 + 1; 𝑦 = 𝑡 3 + 2𝑡
en el punto donde: 𝑡 = −2
Solución:
TASAS DE CAMBIO RELACIONADAS
Estrategia para resolver problemas de tasas de cambio relacionadas.
1) Identificar las magnitudes dadas y las magnitudes a determinar. Asignar símbolos a
esas cantidades.
2) Escribir una ecuación que contenga a las variables cuyos ritmos de cambio son
dados o han de ser determinados.
3) Usando la regla de la cadena, derivar implícitamente ambos lados de la ecuación
con respecto al tiempo t.
4) Después de completar el paso 3, sustituir en la ecuación resultante todos los valores
conocidos de las variables y de los ritmos de cambio. A continuación despejar el
ritmo de cambio que se desea calcular.
• EJEMPLOS
Ejemplo: Inflando un globo
Se bombea aire en el interior de un globo a razón de 4,5 pulgadas cúbicas por minuto. Calcular la razón de cambio del
radio del globo cuando el radio es 2 pulgadas.
Solución:
Ejemplo: La velocidad de un avión detectado por un radar
Un avión vuela por una trayectoria que le llevará a la vertical de una estación de radar. Si s está decreciendo a razón de 400
millas/h cuando s=10 millas, ¿cuál es la velocidad del avión ?
Solución:
𝑥: Trayectoria del avión
𝑠: distancia entre el radar y el avión
𝑑𝑠
𝑚𝑖𝑙𝑙
= −400
;
𝑑𝑡
ℎ𝑜𝑟𝑎
𝑠 = 10
Usamos el teorema de Pitágoras:
𝑠 2 𝑡 = 62 + 𝑥 2 (𝑡)
𝑠 2 𝑡 = 36 + 𝑥 2 𝑡
Si 𝑠 = 10, entonces 𝑥 =?
…..
(1)
Si 𝑠 = 10, entonces 𝑥 =?
102 = 36 + 𝑥 2 𝑡
𝑥 2 = 64
𝑥=8
Derivando (1) respecto a "𝑡“ :
𝑠 2 𝑡 = 36 + 𝑥 2 𝑡
2𝑠
𝑑𝑠
𝑑𝑥
= 2𝑥
𝑑𝑡
𝑑𝑡
2(10)(−400) = 2(8)
𝑑𝑥
𝑑𝑡
𝑑𝑥
= −500
𝑑𝑡
La velocidad del avión es -500 millas / hora.
…..
(1)
ONDAS DE LAGO
• Se deja caer una piedra en un lago en calma, lo que
provoca ondas y círculos. El radio r del círculo exterior está
creciendo a un ritmo constante de 1 pies/s. Cuando el radio
es 4 pies, ¿a qué ritmo está cambiando el área A de la
región circular perturbada?
• Solución:
𝑑𝑟
𝑝𝑖𝑒𝑠
=1
;
𝑑𝑡
𝑠𝑒𝑔
𝐴 𝑡 = 𝜋𝑟 2 𝑡
𝑑𝐴
𝑑𝑟
= 𝜋2𝑟
𝑑𝑡
𝑑𝑡
𝑑𝐴
= 𝜋2(4)(1)
𝑑𝑡
𝑟=4
Á𝑟𝑒𝑎 𝑑𝑒𝑙 𝑐í𝑟𝑐𝑢𝑙𝑜
A: área del círculo
r: radio
CONCLUSIONES
Referencias bibliográficas
• Stewart, J. (2012). Cálculo de una variable: Trascendentes tempranas. (7.a ed). Cengage Learning Editores, S.
A. de C. V.
• Larson, R., Edwards, B. (2011). Cálculo I de una variable. McGRAW-HILL.
• Purcell, E., Varberg D. & Rigdon, S. (2007) Cálculo Diferencial e Integral. México: Pearson Educación.
• Leithold, L. (1998). El Cálculo (7.a ed.). Oxford University Press – Harla México S. A. de C. V.
GRACIAS