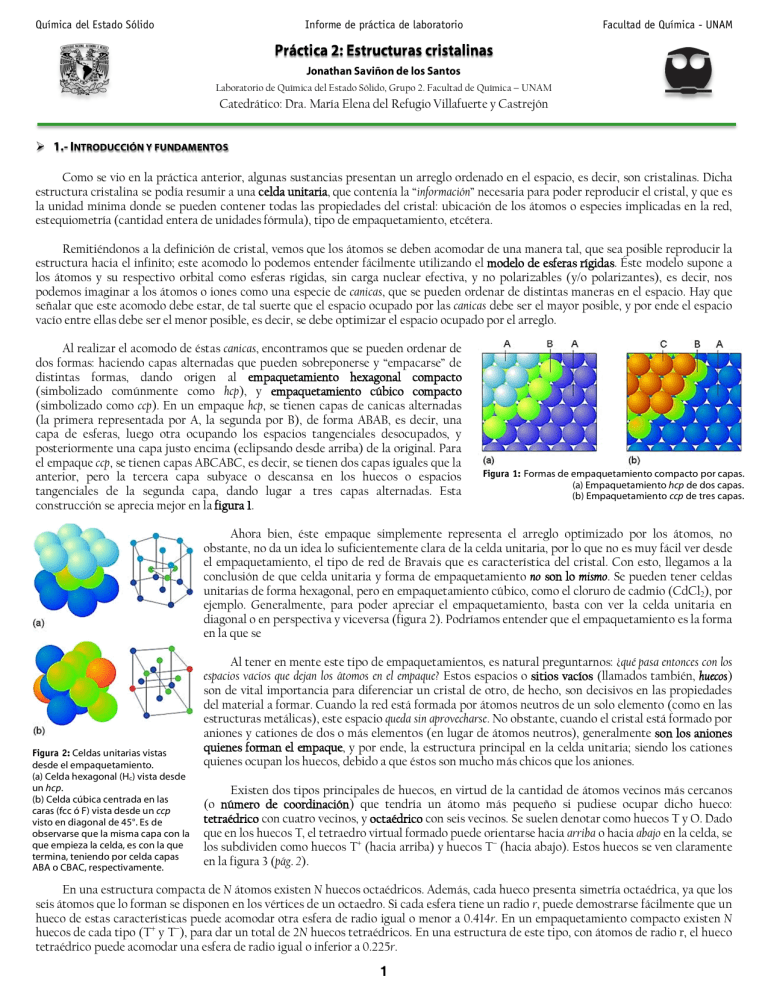
Química del Estado Sólido Informe de práctica de laboratorio Facultad de Química - UNAM Jonathan Saviñon de los Santos Laboratorio de Química del Estado Sólido, Grupo 2. Facultad de Química - UNAM Catedrático: Dra. María Elena del Refugio Villafuerte y Castrejón 1.- INTRODUCCIÓN Y FUNDAMENTOS Como se vio en la práctica anterior, algunas sustancias presentan un arreglo ordenado en el espacio, es decir, son cristalinas. Dicha estructura cristalina se podía resumir a una celda unitaria, que contenía la “información” necesaria para poder reproducir el cristal, y que es la unidad mínima donde se pueden contener todas las propiedades del cristal: ubicación de los átomos o especies implicadas en la red, estequiometría (cantidad entera de unidades fórmula), tipo de empaquetamiento, etcétera. Remitiéndonos a la definición de cristal, vemos que los átomos se deben acomodar de una manera tal, que sea posible reproducir la estructura hacia el infinito; este acomodo lo podemos entender fácilmente utilizando el modelo de esferas rígidas. Éste modelo supone a los átomos y su respectivo orbital como esferas rígidas, sin carga nuclear efectiva, y no polarizables (y/o polarizantes), es decir, nos podemos imaginar a los átomos o iones como una especie de canicas, que se pueden ordenar de distintas maneras en el espacio. Hay que señalar que este acomodo debe estar, de tal suerte que el espacio ocupado por las canicas debe ser el mayor posible, y por ende el espacio vacío entre ellas debe ser el menor posible, es decir, se debe optimizar el espacio ocupado por el arreglo. Al realizar el acomodo de éstas canicas, encontramos que se pueden ordenar de dos formas: haciendo capas alternadas que pueden sobreponerse y “empacarse” de distintas formas, dando origen al empaquetamiento hexagonal compacto (simbolizado comúnmente como hcp), y empaquetamiento cúbico compacto (simbolizado como ccp). En un empaque hcp, se tienen capas de canicas alternadas (la primera representada por A, la segunda por B), de forma ABAB, es decir, una capa de esferas, luego otra ocupando los espacios tangenciales desocupados, y posteriormente una capa justo encima (eclipsando desde arriba) de la original. Para el empaque ccp, se tienen capas ABCABC, es decir, se tienen dos capas iguales que la anterior, pero la tercera capa subyace o descansa en los huecos o espacios tangenciales de la segunda capa, dando lugar a tres capas alternadas. Esta construcción se aprecia mejor en la figura 1. Figura 1: Formas de empaquetamiento compacto por capas. (a) Empaquetamiento hcp de dos capas. (b) Empaquetamiento ccp de tres capas. Ahora bien, éste empaque simplemente representa el arreglo optimizado por los átomos, no obstante, no da un idea lo suficientemente clara de la celda unitaria, por lo que no es muy fácil ver desde el empaquetamiento, el tipo de red de Bravais que es característica del cristal. Con esto, llegamos a la conclusión de que celda unitaria y forma de empaquetamiento no son lo mismo. Se pueden tener celdas unitarias de forma hexagonal, pero en empaquetamiento cúbico, como el cloruro de cadmio (CdCl2), por ejemplo. Generalmente, para poder apreciar el empaquetamiento, basta con ver la celda unitaria en diagonal o en perspectiva y viceversa (figura 2). Podríamos entender que el empaquetamiento es la forma en la que se Figura 2: Celdas unitarias vistas desde el empaquetamiento. (a) Celda hexagonal (Hc) vista desde un hcp. (b) Celda cúbica centrada en las caras (fcc ó F) vista desde un ccp visto en diagonal de 45°. Es de observarse que la misma capa con la que empieza la celda, es con la que termina, teniendo por celda capas ABA o CBAC, respectivamente. Al tener en mente este tipo de empaquetamientos, es natural preguntarnos: ¿qué pasa entonces con los espacios vacíos que dejan los átomos en el empaque? Estos espacios o sitios vacíos (llamados también, huecos) son de vital importancia para diferenciar un cristal de otro, de hecho, son decisivos en las propiedades del material a formar. Cuando la red está formada por átomos neutros de un solo elemento (como en las estructuras metálicas), este espacio queda sin aprovecharse. No obstante, cuando el cristal está formado por aniones y cationes de dos o más elementos (en lugar de átomos neutros), generalmente son los aniones quienes forman el empaque, y por ende, la estructura principal en la celda unitaria; siendo los cationes quienes ocupan los huecos, debido a que éstos son mucho más chicos que los aniones. Existen dos tipos principales de huecos, en virtud de la cantidad de átomos vecinos más cercanos (o número de coordinación) que tendría un átomo más pequeño si pudiese ocupar dicho hueco: tetraédrico con cuatro vecinos, y octaédrico con seis vecinos. Se suelen denotar como huecos T y O. Dado que en los huecos T, el tetraedro virtual formado puede orientarse hacia arriba o hacia abajo en la celda, se los subdividen como huecos T+ (hacia arriba) y huecos T- (hacia abajo). Estos huecos se ven claramente en la figura 3 (pág. 2). En una estructura compacta de N átomos existen N huecos octaédricos. Además, cada hueco presenta simetría octaédrica, ya que los seis átomos que lo forman se disponen en los vértices de un octaedro. Si cada esfera tiene un radio r, puede demostrarse fácilmente que un hueco de estas características puede acomodar otra esfera de radio igual o menor a 0.414r. En un empaquetamiento compacto existen N huecos de cada tipo (T+ y T-), para dar un total de 2N huecos tetraédricos. En una estructura de este tipo, con átomos de radio r, el hueco tetraédrico puede acomodar una esfera de radio igual o inferior a 0.225r. 1 Química del Estado Sólido Informe de práctica de laboratorio Facultad de Química - UNAM Conjuntando las características del empaque, tipo de celda unitaria (o red de Bravais) y los huecos (tanto ocupados como desocupados), se pueden llegar a una gran cantidad de estructuras diferentes. Muchas sustancias, presentan estructuras básicas o estructuras tipo, es decir, estructuras que presentan arreglos muy comunes y análogos en la naturaleza (o también al obtenerlos de forma sintética), con características ya bien caracterizadas de empaque, celda unitaria y huecos ocupados y desocupados. Para facilitar la clasificación de éstas estructuras tipo, los cristaloquímicos y demás estudiosos del tema, las han separado por su estequiometría básica (Ma Xb), ya que así se logra coincidir en tipo de celda unitaria, para analizar las diferencias en el empaque u huecos ocupados. Dichas estructuras, generalmente reciben el nombre del mineral principal o más representativo de dicha estructura. Figura 3: Tipos de huecos en empaquetamiento de esferas y celdas unitarias. Existen también por otra parte, compuestos con la misma composición (o fórmula), pero que presentan distintos arreglos en el espacio, estos son los llamados polimorfos. Un ejemplo bastante común es el sulfuro de zinc (ZnS), donde dos de sus estructuras (una llamada blenda o esfalerita, la otra llamada Wurtzita) presentan la misma cantidad de unidades fórmula en la celda unitaria, sin embargo, simplemente difieren sutilmente: en la orientación de los huecos T ocupados por el Zn, resultando a fin de cuentas, difieren solamente en el tipo de empaque. Generalmente, los polimorfos presentan ésta única diferencia, aunque pueden existir otras diferencias, dependiendo de las especies implicadas en el compuesto o sustancia. (a) En la siguiente tabla, se resumen las propiedades principales mencionadas de éstas estructuras tipo. (b) Tabla 1: Resumen de estructuras tipo con empaquetamiento compacto Coordinación Ejemplo Ejemplo Forma Celda tipo Huecos ocupados (Catión:Anión) empaque ccp empaque hcp 6:6 Todos O NaCl (fcc) NiAs (Hc) MX F (fcc)/Hc ZnS “blenda” (fcc) ZnS “wurtzita” (Hc) 4:4 ½T + + 8:4 (c) MX2 Figura 4: Distintas notaciones para el CdCl2. (a) Modelo de “palitos y bolitas”. (b) Modelo de poliedros. (c) Notación de planta o dibujo en plano (visto en corte con z = 1). 6:3 F (fcc) Hc/ts Hc MX3 6:2 F (fcc) M2X3 6:4 Hc P (sc), tc, fco * 3 ABO 12:6:6 [Huecos T ] [Huecos alternados: T , T-] CaF2 TiO2 “anatasa” (No puede existir) TiO2 “rutilo” (ts) CdCl2 CdI2 YCl3 BiI3 - Al2O3 /3 O - BaTiO3 (tc) /8 T, ½ O [A]T[B2]O O4** [B]T[A,B]O O4** MgAl2O4 “espinela” Mg2SiO4 “olivino” Todos T Todos O ½ O, capas alternadas (ocupado, vacío) 1 /3 O, capas alternadas (ocupado, 2/3 vacío) 2 /3 O 2 [A forma la red] 1 AB2O4* 4:6:6 F (fcc) * En estas estructuras, A representa un catión duro y divalente, B representa un catión blando y generalmente trivalente. ** La notación [A]T indica que la especie A está en huecos T (tetraédricos), [A]O indica que A está en huecos O (octaédricos). Para representar las estructuras, existen distintas notaciones utilizadas en virtud de la información que se desea destacar o analizar de la celda. Las más usuales son modelos de “palitos y bolitas” (o “barras y esferas”) y de poliedros; si se desea dibujarlas en dos dimensiones, se utiliza la notación de planta o dibujo en plano. La primera, se utiliza como un modelo tridimensional exclusivo para la celda unitaria, donde esferas o bolitas representan los átomos o iones, mientras que las barras o palitos representan enlaces y delimitan la celda. En el modelo de poliedros, se suelen representar los huecos ocupados en el empaque, es decir, sirve mejor para apreciar el tipo de empaquetamiento, de tal forma que en el centro del poliedro es el catión (o algunas veces anión) que está en el hueco, y en los vértices los aniones (algunas veces catión) que forman el empaque. Para que el empaque se pueda apreciar, es necesario hacer al menos dos o tres capas de poliedros unidos de tal forma que representen dicho empaque. Por otra parte, en la notación de planta o dibujo en plano, se observa la celda unitaria viéndola ya sea desde arriba, o bien usando planos cristalográficos ya definidos (en ellos se hace una especie de corte a la celda a una determinada altura de la celda y representando lo que se pueda ver hacia arriba y hacia abajo). Al ser dibujo en dos dimensiones, se tiene la necesidad de especificar la posición relativa de los átomos o iones en la tercera dimensión (generalmente la altura), o coordenadas en z, si se representa la celda usando sistema cartesiano (en el plano quedan implícitas las coordenadas x e y). En la figura 4 se presenta a modo de ejemplo, las tres notaciones para la estructura del cloruro de cadmio (CdCl2). En ésta práctica, se verán diez estructuras tipo como éstas, más a detalle. 2 Química del Estado Sólido Informe de práctica de laboratorio Facultad de Química - UNAM 2.- RESULTADOS En ésta práctica se expusieron 10 estructuras cristalinas, las cuales, se hace un resumen breve de sus características a continuación. Se anexa una tabla donde se resume la información esencial de la estructura. En todas se emplearon modelos de “palitos y bolitas” y de poliedros, exceptuando la estructura de la Espinela; en cada una se señalan las diferencias y sus respectivas ventajas y desventajas. 2.1.- Sal de roca o Halita (NaCl) Nombre químico y fórmula: NaCl, cloruro de sodio. Nombres comunes o tradicionales: Cloruro sódico, sal de roca, sal gema, halita, sal de mesa, sal de mar. Cálculo de densidad teórica: Para el NaCl, con celda cúbica, se tiene: a = 5.62279 × 10-8 cm. El volumen de la celda cúbica está dado por: Vcelda a3 . Tabla 2: Resumen de datos para NaCl (halita) Polimorfos No tiene Coordinación (Catión:Anión) 6:6 Unidades fórmula en celda (z) 4 ¿Eléctricamente neutra? Sí Densidad (valor aceptado) 2.165 g/cm3 Densidad (valor calculado) 2.184 g/cm3 Celda tipo/Empaque F (fcc)/ccp Por tanto, se tiene una densidad teórica de: dteórica (4 u.f. /celda)(58.44 g/ mol NaCl) (5.62279 108 cm)3 (6.02214 1023 u.f. / mol ) 2.184 g/cm 3 celda NaCl Dado que no hay polimorfos, no varía la densidad. ¿Cuál de los diferentes modelos cree que es el más representativo para éste compuesto? El de “palitos y bolitas”, ya que así se puede apreciar mucho mejor la simetría en la distribución de los átomos en la celda, además que fácilmente se puede apreciar el empaque, viéndola en diagonal, sin necesidad de poliedros. Modelos de “palitos y bolitas” y de poliedros: Notación de planta: Cl- formando el empaque. Además de su ya bastate conocido uso como aditivo alimenticio, se utiliza como persevante de alimentos (en salmuera), también se suele usar como fundente de nieve en lugares muy fríos y en la preparación de bebidas energizantes, así como electrolito en aplicaciones electroanalíticas. 2.2.- Fluorita (CaF2) Nombre químico y fórmula: CaF2, fluoruro de calcio. Nombres comunes o tradicionales: Fluoruro cálcico, fluorita. Cálculo de densidad teórica: Para el CaF2, con celda cúbica, se tiene: a = 5.363 × 10-8 cm. El volumen de la celda cúbica está dado por: Vcelda a3 . Tabla 3: Resumen de datos para CaF2 (fluorita) Polimorfos No tiene Coordinación (Catión:Anión) 8:4 Unidades fórmula en celda (z) 4 ¿Eléctricamente neutra? Sí Densidad (valor aceptado) 3.36 g/cm3 Densidad (valor calculado) 3.36 g/cm3 Celda tipo/Empaque F (fcc)/ccp Por tanto, se tiene una densidad teórica de: dteórica (4 u.f. /celda)(78.07 g/ mol CaF2 ) (5.363 108 cm)3 (6.02214 1023 u.f. / mol ) Dado que no hay polimorfos, no varía la densidad. 3 3.362 g/cm 3 celda CaF2 Química del Estado Sólido Informe de práctica de laboratorio Facultad de Química - UNAM ¿Cuál de los diferentes modelos cree que es el más representativo para éste compuesto? Si bien el de palitos y bolitas muestra claramente que los iones Ca2+ se encuentran de forma alternada, el modelo de poliedros hace más énfasis no sólo en la ocupación de estos huecos cúbicos, sino también del empaque. Por tanto, se concluye que para la fluorita, es mejor el modelo de poliedros. Modelos de “palitos y bolitas” y de poliedros: Notación de planta: F- formando el empaque. Es la principal fuente de producción del ácido fluorhídrico (empleado ampliamente en la industria del vidrio y el acero), además de que puede ser usado directamente en las pastas dentales para enriquecerlas con fluoruro (agente anticaries). 2.3.- Rutilo (TiO2) Nombre químico y fórmula: TiO2, óxido de titanio (IV). Nombres comunes o tradicionales: Rutilo, dióxido de titanio, óxido titánico. Cálculo de densidad teórica: Para el TiO2, con celda tetragonal simple (ts), se tiene: a = b = 4.593 × 10-8 cm, c = 2.959 × 10-8 cm. El volumen de la celda (ts) está dado por: Vcelda a2c . Por tanto, se tiene una densidad teórica de: dteórica Tabla 4: Resumen de datos para TiO2 (rutilo) 2: “anatasa” con ccp, Polimorfos “brookita” (os) Coordinación (Catión:Anión) 6:3 Unidades fórmula en celda (z) 2 ¿Eléctricamente neutra? Sí Densidad (valor aceptado) 4.250 g/cm3 Densidad (valor calculado) 4.118 g/cm3 Celda tipo/Empaque ts/hcp (4 u.f. /celda)(79.88 g/ mol TiO2 ) 8 (4.593 10 cm)2 (2.959 108 cm)(6.02214 1023 u.f. / mol ) 4.118 g/cm 3 celda TiO2 La densidad reportada de la anatasa es de 3.90 g/cm3 y la de la brookita es de 4.12 g/cm3, con lo que podemos ver que el polimorfo más denso es el rutilo, seguido por la brookita, y el menos denso es la anatasa. ¿Cuál de los diferentes modelos cree que es el más representativo para éste compuesto? Aquí se prefiere el de poliedros, ya que así se aprecia mucho mejor el arreglo de los octaedros desviados que forman el empaque. Modelos de “palitos y bolitas” y de poliedros: Notación de planta: Ti4+ formando la red. El dióxido de titanio tiene una amplia gama de aplicaciones y usos: pigmento blanco en pinturas, elaboración de cerámicos (generalmente de tipo Perovskitas), industria farmacéutica, aeronáutica, metalúrgica, papelera e incluso cosméticos. 4 Química del Estado Sólido Informe de práctica de laboratorio Facultad de Química - UNAM 2.4.- Blenda de zinc o Esfalerita (ZnS) Nombre químico y fórmula: ZnS, sulfuro de zinc. Nombres comunes o tradicionales: Blenda de zinc, esfalerita. Cálculo de densidad teórica: Para el ZnS, con celda cúbica, se tiene: a = 5.409 × 10-8 cm. El volumen de la celda cúbica está dado por: Vcelda a3 . Tabla 5: Resumen de datos para ZnS (blenda) Polimorfos 1: “wurtzita” con hcp Coordinación (Catión:Anión) 4:4 Unidades fórmula en celda (z) 4 ¿Eléctricamente neutra? Sí Densidad (valor aceptado) 4.09 g/cm3 Densidad (valor calculado) 4.080 g/cm3 Celda tipo/Empaque F (fcc)/ccp Por tanto, se tiene una densidad teórica de: dteórica (4 u.f. /celda)(97.46 g/ mol ZnS) (5.409 10 8 cm)3 (6.02214 1023 u.f. / mol ) 4.080 g/cm 3 celda ZnS La densidad reportada de la wurtzita es de 4.03 g/cm3, siendo el polimorfo más denso (para el ZnS) la blenda. ¿Cuál de los diferentes modelos cree que es el más representativo para éste compuesto? Aquí se prefiere el de poliedros, ya que así se aprecia mucho mejor el arreglo de los tetraedros (T+) formando el empaque ccp. Modelos de “palitos y bolitas” y de poliedros: Notación de planta: Zn2+ formando el empaque. La blenda de zinc es la forma principal de obtención del Zn elemental, aunque también se aprovecha ésta forma mineral sobre todo en aplicaciones de galvanotecnia y galvanoplastia. También suele ser usado como agente vulcanizante en llantas. 2.5.- Wurtzita (ZnS) Nombre químico y fórmula: ZnS, sulfuro de zinc. Nombres comunes o tradicionales: Wurtzita. La wurtzita se diferencia de la blenda simplemente por el tipo de empaquetamiento, esto dado en virtud de que en ésta estructura, se van alternando los huecos ocupados T+ con T-, dando como resultado capas ABAB, con hcp. Esta diferencia también ocasiona que el valor z de unidades fórmula contenidas en la celda cambie de 4 a 2. Tabla 6: Resumen de datos para ZnS (wurtzita) Polimorfos 1: “blenda” con ccp Coordinación (Catión:Anión) 4:4 Unidades fórmula en celda (z) 2 ¿Eléctricamente neutra? Sí Densidad (valor aceptado) 4.03 g/cm3 Densidad (valor calculado) 4.080 g/cm3 Celda tipo/Empaque Hc/hcp Cálculo de densidad teórica: Para el ZnS, con celda hexagonal, se tiene: a = 3.822 × 10-8 cm, c = 6.260 × 10-8 cm. El volumen de la celda hexagonal está dado por: Vcelda 23 a2 c . Por tanto, se tiene una densidad teórica de: dteórica (2 u.f. /celda)(97.46 g/ mol ZnS) ( 3 8 2 8 23 2 (3.822 10 cm) (6.260 10 cm))(6.02214 10 u.f. / mol ) 4.080 g/cm 3 celda ZnS Es de observarse que el valor teórico fue casualmente el mismo con 4 cifras significativas, no obstante, el valor experimental indica una diferencia sutil, como se vio para el valor de la blenda, comparado con el de la wurtzita. 5 Química del Estado Sólido Informe de práctica de laboratorio Facultad de Química - UNAM ¿Cuál de los diferentes modelos cree que es el más representativo para éste compuesto? Aquí se prefiere el de poliedros, ya que así se aprecia mucho mejor el arreglo de los tetraedros (T+ y T- alternados) formando el empaque hcp. Modelos de “palitos y bolitas” y de poliedros: Notación de planta: S2- formando el empaque. A pesar de ser ZnS, ésta forma tiene usos distintos al de la blenda; por ejemplo, se suele utilizar como pigmento en algunas pinturas, en la “cruz de malta” en los tubos de rayos catódicos (CRT), pantallas que funcionen a CRT. 2.7.- Cloruro de cadmio (CdCl2) Nombre químico y fórmula: CdCl2, cloruro de cadmio (II). Nombres comunes o tradicionales: dicloruro de cadmio, cloruro cadmioso. Cálculo de densidad teórica: Para el CdCl2, con celda hexagonal, se tiene: a = 3.846 × 10-8 cm, c = 17.479 × 10-8 cm. El volumen de la celda hexagonal está dado por: Vcelda 23 a2 c . Tabla 7: Resumen de datos para CdCl2 Polimorfos No tiene Coordinación (Catión:Anión) 6:3 Unidades fórmula en celda (z) 3 ¿Eléctricamente neutra? Sí Densidad (valor aceptado) 4.047 g/cm3 Densidad (valor calculado) 4.017 g/cm3 Celda tipo/Empaque Hc/ccp Por tanto, se tiene una densidad teórica de: dteórica (3 u.f. /celda)(183.32 g/ mol CdCl2 ) ( 3 8 2 8 23 2 (3.846 10 cm) (17.749 10 cm))(6.02214 10 u.f. / mol ) 4.0173 g/cm 3 celda CdCl2 Dado que no hay polimorfos, no varía la densidad. ¿Cuál de los diferentes modelos cree que es el más representativo para éste compuesto? El de poliedros, debido a que aquí se hace explícita la forma en la que se dejan los huecos octaédricos por capas, es decir, se aprecia mucho mejor el empaque y la coordinación del ión Cd2+. Modelos de “palitos y bolitas” y de poliedros: Notación de planta: Cd2+ en los vértices de celda. 6 Química del Estado Sólido Informe de práctica de laboratorio Facultad de Química - UNAM En el laboratorio, usualmente se utiliza como preparativo para compuestos organometálicos, así como fotocopiado (juntos con compuestos de selenio) y electroplatinado. Antiguamente se usaba como pigmento y colorante inorgánico, pero posteriormente se descubrió su alta toxicidad para los seres vivos, por lo que se ha restringido su uso. 2.7.- Niquelita (NiAs) Nombre químico y fórmula: NiAs, arseniuro de níquel (III). Nombres comunes o tradicionales: Niquelita. Cálculo de densidad teórica: Para el NiAs, con celda hexagonal, se tiene: a = 3.618 × 10-8 cm, c = 5.034 × 10-8 cm. El volumen de la celda hexagonal está dado por: Vcelda 23 a2 c . Tabla 8: Resumen de datos para NiAs (niquelita) Polimorfos No tiene Coordinación (Catión:Anión) 6:6 Unidades fórmula en celda (z) 2 ¿Eléctricamente neutra? Sí Densidad (valor aceptado) 7.78 g/cm3 Densidad (valor calculado) 7.772 g/cm3 Celda tipo/Empaque Hc/hcp Por tanto, se tiene una densidad teórica de: dteórica (2 u.f. /celda)(133.61 g/ mol NiAs) ( 23 (3.618 108 cm)2 (5.034 10 8 cm))(6.02214 1023 u.f. / mol ) 7.772 g/cm 3 celda NiAs Dado que no hay polimorfos, no varía la densidad. ¿Cuál de los diferentes modelos cree que es el más representativo para éste compuesto? En este caso resultó mejor el modelo de palitos y bolitas, ya que aquí se puede apreciar mejor la delimitación de la celda hexagonal, y como se vio en la introducción, facilita la visualización del empaque, no obstante, en el modelo de poliedros, se hace explícito el hueco octaédrico ocupado por el Ni3+. Modelos de “palitos y bolitas” y de poliedros: Notación de planta: Se muestran las 4 celdas para facilitar la visualización del Ni3+ con coordinación 6 en el plano. As3- forma la red. Debido a la presencia de arsénico en el compuesto, sus usos han quedado bastante restringidos, a únicamente una parte de la industria siderúrgica específica. 2.8.- Corindón (Al2O3) Nombre químico y fórmula: Al2O3, óxido de aluminio. Nombres comunes o tradicionales: Corindón, corundo, Ń-alúmina. Cálculo de densidad teórica: Para el Al2O3, con celda hexagonal, se tiene: a = 4.785 × 10-8 cm, c = 12.991 × 10-8 cm. El volumen de la celda hexagonal está dado por: Vcelda 23 a2 c . Tabla 9: Resumen de datos para Al2O3 (corindón) 2: β y ʼn alúmina Polimorfos Coordinación (Catión:Anión) 6:4 Unidades fórmula en celda (z) 6 ¿Eléctricamente neutra? Sí Densidad (valor aceptado) 4.05 g/cm3 Densidad (valor calculado) 3.937 g/cm3 Celda tipo/Empaque Hc/hcp Por tanto, se tiene una densidad teórica de: dteórica (6 u.f. /celda)(101.96 g/ mol Al2O3 ) ( 3 8 2 8 23 2 (4.785 10 cm) (12.991 10 cm))(6.02214 10 u.f. / mol ) 3.937 g/cm 3 celda Al2O3 Para los polimorfos β y ʼn que tienen densidad de 3.78 g/cm3, se observa que la forma Ń o de corindón es más densa. 7 Química del Estado Sólido Informe de práctica de laboratorio Facultad de Química - UNAM ¿Cuál de los diferentes modelos cree que es el más representativo para éste compuesto? Aquí se prefiere el de poliedros, ya que así se aprecia mucho mejor el arreglo de los octaedros, y se hace evidente que 2/3 de las capas de octaedros están vacíos. Modelos de “palitos y bolitas” y de poliedros: Notación de planta: O2- formando la red. Uno de los principales usos del corindón como mineral es como aislante térmico y soporte en catalizadores, además de pulidor en aceros duros. Si el mineral presenta trazas de Cr3+ y otros metales, entonces forma piedras preciosas, tales como el rubí o el zafiro. 2.9.- Perovskita de bario (BaTiO3) Tabla 10: Resumen de datos para BaTiO3 (perovskita) Polimorfos No tiene Coordinación (Catión:Anión) 12:6:6 Unidades fórmula en celda (z) 1 Para las estructuras tipo Perovskita, es variable el tipo de celda a formar; por ¿Eléctricamente neutra? Sí ejemplo: el CaTiO3 forma una celda ortorrómbica, el BaTiO3 una tetragonal, por su Densidad (valor aceptado) 6.021 g/cm3 parte, el SrTiO3 forma una celda cúbica perfecta. Esto es debido a la diferencia que Densidad (valor calculado) 6.020 g/cm3 existe entre el radio del catión alcalinotérreo (A2+) y el O2-, y que además, el Celda tipo/Empaque tc/hcp Nombre químico y fórmula: BaTiO3, trioxotitanato (IV) de bario. Nombres comunes o tradicionales: titanato de bario, Perovskita de bario. empaquetamiento formado puede cambiar con la temperatura. En todas se mantiene o se ajusta el octaedro formado por el catión central Ti4+ rodeado de 6 aniones O2-. Cálculo de densidad teórica: Para el BaTiO3, con celda tetragonal (tc), se tiene: a = b = 3.992 × 10-8 cm, y c = 4.036 × 10-8 cm. El volumen de la celda tetragonal está dado por: Vcelda a2c . Por tanto, se tiene una densidad teórica de: dteórica (1 u.f. /celda)(233.21 g/ mol BaTiO3 ) 8 ((3.992 10 cm)2 (4.036 10 8 cm))(6.02214 1023 u.f. / mol ) 6.020 g/cm 3 celda BaTiO3 Dado que no hay polimorfos, no varía la densidad. ¿Cuál de los diferentes modelos cree que es el más representativo para éste compuesto? Para estas estructuras, resulta mucho más visual el modelo de palitos y bolitas, ya que así se aprecia mucho mejor la coordinación de ambos cationes metálicos. No obstante, también el modelo de poliedros brinda una fácil visualización de los huecos desocupados, además que hace más visible el que los octaedros no están alineados perfectamente, sino que están inclinados; en ciencia de materiales, esta inclinación, es decisiva en las propiedades de la Perovskita. Modelos de “palitos y bolitas” y de poliedros: 8 Química del Estado Sólido Informe de práctica de laboratorio Facultad de Química - UNAM Notación de planta: Ba2+ formando la red F (fcc) Las Perovskitas, al ser cerámicos, pueden tener una gran cantidad de aplicaciones. Actualmente son objeto de investigación, ya que debido a la manipulación del catión central en la estructura, puede lograrse que no esté centrado (una coordenada distinta de (½, ½, ½) en la celda) y da lugar a distintas estructuras, con propiedades muy interesantes: superconductividad, ordenamiento o configuración multiferróica (presentar simultáneamente ferroelectricidad, ferromagnetismo, ferroelasticidad, o al menos dos de ellas), luminiscencia, y una larga lista de etcétera. 2.10.- Espinela (MgAl2O4) MgAl2O4, dialuminato de magnesio, tetraoxodialuminato de magnesio u óxido de aluminio y magnesio. Nombres comunes o tradicionales: Espinela. Nombre químico y fórmula: Tabla 11: Resumen de datos para MgAl2O3 (espinela) Polimorfos No Coordinación (Catión:Anión) 4:6:6 Unidades fórmula en celda (z) 8 ¿Eléctricamente neutra? Sí Densidad (valor aceptado) 3.580 g/cm3 Densidad (valor calculado) 3.583 g/cm3 Celda tipo/Empaque F (fcc)/ccp Esta estructura se puede entender como una principal de tipo F (fcc), con otras cuatro en su interior, que son dos cubos irregulares y dos tetraedros regulares, distribuidos alternadamente en el los cuadrantes del cubo F (fcc) principal. Estas cuatro estructuras secundarias en el interior, dan origen a que la estructura tenga una cantidad muy singular de huecos: la mitad de los huecos O, y tan sólo una octava parte de los huecos T (un T+, por un T-). El tipo de empaquetamiento que presenta éste compuesto en específico es ccp, pero también puede existir el hcp (Mg2SiO4, conocido como “olivino”). Para ésta estructura únicamente se construyó el modelo de palitos y bolitas. Cálculo de densidad teórica: Para el MgAl2O3, con celda cúbica, se tiene: a = 8.08 × 10-8 cm. El volumen de la celda cúbico está dado por: Vcelda a3 . Por tanto, se tiene una densidad teórica de: dteórica (8 u.f. /celda)(142.27 g/ mol MgAl2 O4 ) (8.08 108 cm)3 (6.02214 1023 u.f. / mol ) 3.583 g/cm 3 celda MgAl2 O4 Dado que no hay polimorfos, no varía la densidad. ¿Cuál de los diferentes modelos cree que es el más representativo para éste compuesto? Para estas estructuras, resulta mucho más visual el modelo de palitos y bolitas, ya que así se aprecia mucho mejor la coordinación de ambos cationes metálicos. El representar la espinela como una estructura principal y otras secundarias alternadas es una forma sencilla y didáctica de representar una estructura tan intrincada como esta, donde a pesar de que visualmente no resalte, si se logran apreciar los huecos, coordinaciones y forma de empaquetamiento con respecto a la estructura principal. Modelos de “palitos y bolitas” y de poliedros: 9 Química del Estado Sólido Informe de práctica de laboratorio Facultad de Química - UNAM Notación de planta en (1 0 0): Mg2+ formando la red F (fcc) principal. Las espinelas generalmente se encuentran en una zona relativamente profunda de la corteza terrestre, incluso hasta 6 km debajo. Dada la gran gama de colores que pueden presentar las estructuras tipo espinela, muchas vecen eran usadas como sustitutos más económicos de piedras preciosas o gemas, propiamente, sustituto del rubí o del zafiro. Aún se sigue utilizando en joyería como en sortijas, cadenas, dijes, collares, etcétera. Cuando alguna estructura de este tipo resulta ser muy dura para el trabajo artesanal de joyería, se remite a su uso en mecanismos de relojería fina, como abrasivo de minerales y aceros, así como de cerámicos superelásticos. 3.- OBSERVACIONES Y CONCLUSIONES En ésta práctica se observó cómo es el arreglo en distintas estructuras tipo muy comunes en la Química del Estado Sólido. Se vieron como los distintos tipos de modelos nos proporcionaban distinta información sobre la estructura; siendo el más apto para la mayoría de ellas, el modelo con poliedros: tiene la capacidad de mostrarnos no sólo los huecos ocupados, sino da una idea clara de cómo es el empaque, sobre todo para estructuras con capas vacías y alternadas. Aunque también fue necesario, algunas veces, recurrir mejor al modelo de “palitos y bolitas”, para tener siempre una idea de la celda unitaria, así como determinar el factor z de unidades fórmula en dicha celda unitaria. También se calcularon densidades teóricas a partir de datos duros de parámetros de red consultados en la literatura y ecuaciones sencillas, y se vio en general, una buena concordancia entre el valor calculado y el valor aceptado o reportado en la literatura. Algo particular que hay que destacar, que durante la realización de la práctica, muchos equipos no presentaron todos los putos que se pedían en el protocolo, siendo la falta más recurrente, la ausencia de la notación de planta en muchas estructuras (sobre todo para la espinela, donde no fue posible hallar información confiable), y los contantes errores en la exposición de la estructura de la sal de roca; esto se puede mejorar con una mejor preparación del material de estudio asignado. En conclusión, podemos decir que el modelo de empaquetamiento de esferas rígidas, a pesar de sus limitaciones como teoría de enlace, funciona muy bien para relaciones geométricas en las estructuras cristalinas, haciéndolo útil para el estudio de éstas. También es importante destacar la utilidad de las estructuras tipo: conociendo unas pocas estructuras, se pueden deducir y ver analogías con muchas otras, en función de su estequiometría, empaque o tipo de celda. 4.- CUESTIONARIO A continuación, se reporta el cuestionario completo y desarrollado para la estructura asignada: cloruro de cadmio (II), CdCl2. 1.- a) Anote la fórmula del compuesto y el nombre químico de la estructura construida. b) nombre trivial del compuesto. a) CdCl2, cloruro de cadmio (II) b) Dicloruro de cadmio, cloruro cadmioso 2.- El compuesto anterior presenta 0 (cero) polimorfos. Presenta un empaquetamiento cúbico compacto (ccp), a diferencia del yoduro de cadmio (CdI2), que presenta un empaquetamiento hexagonal compacto (hcp); no obstante, no puede ser considerado polimorfo, debido a que son dos sustancias diferentes. 3.- La estructura construida está representada por un modelo de: Un modelo de “palitos y bolitas” y otro de poliedros. 10 Química del Estado Sólido Informe de práctica de laboratorio Facultad de Química - UNAM 4.- Explique una ventaja y una desventaja de este modelo de representación. El modelo de “palitos y bolitas” en este caso nos permitía ver directamente la coordinación tanto para Cd2+ y Cl-, facilitando el conteo de unidades fórmula (z) en la celda; más en cambio, no era posible apreciar del todo la alternancia de sitios octaédricos vacíos en la celda, característico del empaque en el CdCl2. El modelo de poliedros nos permitió ver muy fácilmente las capas de octaedros ocupados y vacíos que se iban alternando, al margen de las aristas ecuatoriales de cada uno; no obstante, no describía por completo la coordinación del Cl- y no daba idea alguna de la forma de la celda unitaria. 5.- Anote el número de coordinación de las especies involucradas. Coordinación para Cd2+: 6 (sitios octaédricos), para Cl-: 3 (sitios piramidales triangulares). 6.- ¿La estructura está eléctricamente neutra? Sí, se tienen en total 6 cargas negativas (3[2(1-)]) y 6 cargas positivas (3[1(2+)]) en la celda unitaria. 7.- Determine el número de unidades formulares (z) del compuesto en la celda unitaria. Para el CdCl2, z = 3 unidades fórmula, es decir, en total hay 3 iones Cd2+ y 6 iones Cl-. 8.- a) Calcule la densidad teórica del compuesto y compárela con los datos de un manual. b) ¿Varía el valor de un polimorfo a otro? a) Se tiene que la densidad teórica se calcula de la siguiente manera: dteórica z M Vcelda NA Para el CdCl2, con celda hexagonal, se tienen: a = 3.846 × 10-8 cm, c = 17.479 × 10-8 cm, ʼn = 120° (Ń = β = 90°). El volumen de la celda hexagonal está dado por: 3 Vcelda a2c 2 Por tanto, se tiene una densidad teórica determinada por (u.f. = unidades fórmula): dteórica (3 u.f. /celda)(183.32 g/ mol CdCl2 ) ( 3 8 2 8 23 2 (3.846 10 cm) (17.749 10 cm))(6.02214 10 u.f. / mol ) 4.0173 g/cm 3 celda CdCl2 Éste valor, comparado con el aceptado en la literatura (de d = 4.047 g/cm3), se tiene un error de apenas 0.735 %, el cuál es bastante aceptable y despreciable. b) No varía, debido a que no hay polimorfos del CdCl2. 9.- ¿Cuál de los diferentes modelos cree usted que es el más representativo para su compuesto? El de poliedros, debido a que aquí se hace explícita la forma en la que se dejan los huecos octaédricos por capas, es decir, se aprecia mucho mejor el empaque y la coordinación del ión Cd2+. 10.- Dibuje la estructura asignada en: a) Modelo poliedral (Vista en perspectiva al empaque, en los vértices de los octaedros se encuentran los iones Cl-) 11 Química del Estado Sólido Informe de práctica de laboratorio Facultad de Química - UNAM b) Modelo de esferas y barras (Vista de pedestal, a 45° de la anterior, en vértices de celda unitaria: Cd2+) (Celda unitaria en perspectiva al empaque (inclinada)) 11.- Anote las coordenadas fraccionarias y/o posiciones atómicas de las especies involucradas en la estructura. Se muestra a continuación: 1, 0 Leyenda: /12, 11/12 1, 0 3 /12, 9/12 - Iones Cl 3 /12, 9/12 4 /12 Iones Cd2+ en vértices de celda (formando el empaque) Iones Cd2+ en el interior de celda, ocultos por Cl- 5 8 /12 3 /12, 9/12 Cd2+ en los vértices de celda. 3 /12, 9/12 1 /12, 7/12 1, 0 1, 0 12.- Mencione al menos dos aplicaciones del compuesto cuyo modelo construyó. En el laboratorio, usualmente se utiliza como preparativo para compuestos organometálicos, así como fotocopiado (juntos con compuestos de selenio) y electroplatinado. Antiguamente se usaba como pigmento y colorante inorgánico, pero posteriormente se descubrió su alta toxicidad para los seres vivos, por lo que se ha restringido su uso, o incluso erradicado. 5.- REFERENCIAS SMART, “Química del estado sólido”, Adisson-Wesley.1995. WEST. “Basic Solid State Chemistry”, John Wiley & Sons editores, 1a ed., 1988. CALLISTER, “Ciencia e ingeniería de materiales”, Reverté S.A. http://www.luc.edu/faculty/spavko1/minerals/tom.htm Sands, E. (1993). Introducción a la cristalografía. España: Reverté. http://roble.pntic.mec.es/~jfes0017/mineral.php?letra=w&orden=4012#4012 http://ocw.uniovi.es/file.php/39/1C_C11812_A/cristalografia/7/6_3.htm http://www.redoptronics.com/BaTio3-crystal.html http://webmineral.com/data/Corundum.shtml http://www.ehu.es/zorrilla/juanma/T8EIonico.pdf http://wwwchem.uwimona.edu.jm/courses/cdcl2J.html 12