7ºBásico
Los Números
Enteros
(Unidad 1)
OBJETIVO DE LA CLASE:
Caracterizar el conjunto de los números enteros.
CONTENIDOS:
•
•
•
•
Historia de los números enteros y los números
negativos
Orden en la recta numérica
Opuestos
Valor Absoluto
¿Cuánto es?
7 – 3=
¿Y ahora?
¿Cuánto es?
3 – 7=
Breve historia de los números enteros
ü
ü
Con la civilización hindú aparecen los
números enteros.
En el año 628 el matemático hindú
Brahamagupta publica su obra donde
destacan:
•
Las primeras reglas para sumar
números negativos.
•
La distinción entre ”los bienes”, “las
deudas” y la “la nada”, es decir,
números positivos, ngaetivos y cero.
Breve historia de los números enteros
ü
ü
ü
La aparición de los números negativos
tuvo cierta resistencia en un inicio en el
Siglo XVII, fueron denominados
números absurdos o ficticios.
Hasta el Siglo XVIII, los números
negativos son entendidos como los
opuestos de los positivos.
Pero recién el el Siglo XIX los números
enteros fueron aceptados como una
extensión del conjunto de los números
naturales.
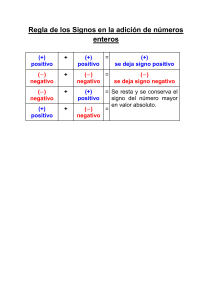
Definición de los enteros
Los números enteros se denotan con el símbolo ℤ.
Está formado por:
- Los números naturales o enteros positivos
- Los enteros negativos
- Y el cero o neutro.
ℤ={…, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, …}
La Z es por “Zahl” que significa “Número” en alemán.
Orden en la recta númerica
A la izquierda están ubicados los negativos, a la derecha los positivos y en
el centro el cero o neutro.
NEGATIVOS
●
●
NEUTRO
POSITIVOS
Los enteros negativos son siempre antecedidos por un signo negativo (-).
Mientras que los positivos pueden o no llevar el signo (+).
Siempre será menor el número que esté a la izquierda de otro.
Orden en los enteros
● Todo número entero que esté a la derecha de otro en la recta numérica,
es mayor que él.
● Todo número entero que esté a la izquierda de otro en la recta
numérica, es menor que él.
● Todo número negativo es menor que cero.
● Todo número positivo es mayor que cero.
● Todo número negativo es menor que cualquier número positivo.
Practiquemos lo
anterior…
Actividad 1: Utiliza los signo “Mayor que” (>) o “Menor que” (<)
para establecer el orden de los siguientes números enteros.
A) 5 _____ 6
B) -3 _____ -2
C) -1 _____ 0
D) 8 ______ 0
E) -2 _____ -6
F) 10 _____ -7
Mira la imagen
durante 15
segundos
Anota en tu cuaderno
una lista de los objetos
que contenía la
mochila
Tienes 1 minuto para recordar
Opuestos en los enteros
Los opuestos en los enteros se refiere a los mismos números, pero
con distinto signo.
Ejemplo:
-5 es el opuesto de 5 ó 5 es el opuesto de -5
6 es el opuesto de -6 ó -6 es el opuesto de 6
Si te fijas los números opuestos se encuentran a la misma distancia del cero.
Actividad 2: Escribe el opuesto de cada entero.
A) El opuesto de -5 es ____
B) El opuesto de 10 es ____
C) El opuesto de 1 es ____
D) El opuesto de -25 es ____
E) El opuesto de 0 es ____
F) El opuesto de 500 es ____
Valor absoluto | z |
El valor absoluto de un número entero se denota con dos líneas
verticales |z|. Es el valor que representa la distancia entre el número
y el cero, por lo que el valor absoluto siempre es positivo o cero.
Por ejemplo:
● La distancia de -3 al 0 son 3 unidades.
● La distancia de 3 al 0 son 3 unidades
● Por lo tanto, el valor absoluto de -3 y 3 son iguales, porque ambos
están a 3 unidades del cero.
Actividad 3: Escribe el valor absoluto de los siguientes números
enteros
A) | 5 | =
B) | -10 | =
C) | 0 | =
D) | 3000 | =
E) | -23 | =
F) | 1 | =
En resumen: Calcular el valor absoluto de un número es
dejarlo SIEMPRE positivo (sin signo)
REVISIÓN ACTIVIDAD “Haz Ahora”
WORDWALL
RESUMEN
●
VEAMOS UN BREVE VIDEO
EL SENSEI DE LAS MATES: https://www.youtube.com/watch?v=cmXRuR7X1bs
Conclusión
El conjunto de los números enteros (Z) surge como una necesidad de llenar
algunos vacíos que existían al trabajar con los números naturales.
Por ejemplo, en el caso de:
Resolver sustracciones donde el minuendo es menor que el sustraendo, como
3 – 7 = ¿?
• Expresar la pérdida de dinero en un negocio.
• Señalar temperaturas bajo cero, indicar las profundidades bajo el nivel del
mar, u otras situaciones.
•
•
El opuesto de un número entero es el mismo número pero con el signo
cambiado.
El valor absoluto de un número entero es dejar el número sin signo, o sea
siempre positivo.
Resuelve en tu
Cuaderno de
Actividades
desde la página 6
hasta la página 10
CUADERNO DE ACTIVIDADES
PÁGINA 6
CUADERNO DE ACTIVIDADES
PÁGINA 6
CUADERNO DE ACTIVIDADES
PÁGINA 6
CUADERNO DE ACTIVIDADES
PÁGINA 7
CUADERNO DE ACTIVIDADES
PÁGINA 7
CUADERNO DE ACTIVIDADES
PÁGINA 7
CUADERNO DE ACTIVIDADES
PÁGINA 8
CUADERNO DE ACTIVIDADES
PÁGINA 8
CUADERNO DE ACTIVIDADES
PÁGINA 8
CUADERNO DE ACTIVIDADES
PÁGINA 9
CUADERNO DE ACTIVIDADES
PÁGINA 9
CUADERNO DE ACTIVIDADES
PÁGINA 9
CUADERNO DE ACTIVIDADES
PÁGINA 9
CUADERNO DE ACTIVIDADES
PÁGINA 10
CUADERNO DE ACTIVIDADES
PÁGINA 10
CUADERNO DE ACTIVIDADES
PÁGINA 10
CUADERNO DE ACTIVIDADES
PÁGINA 10