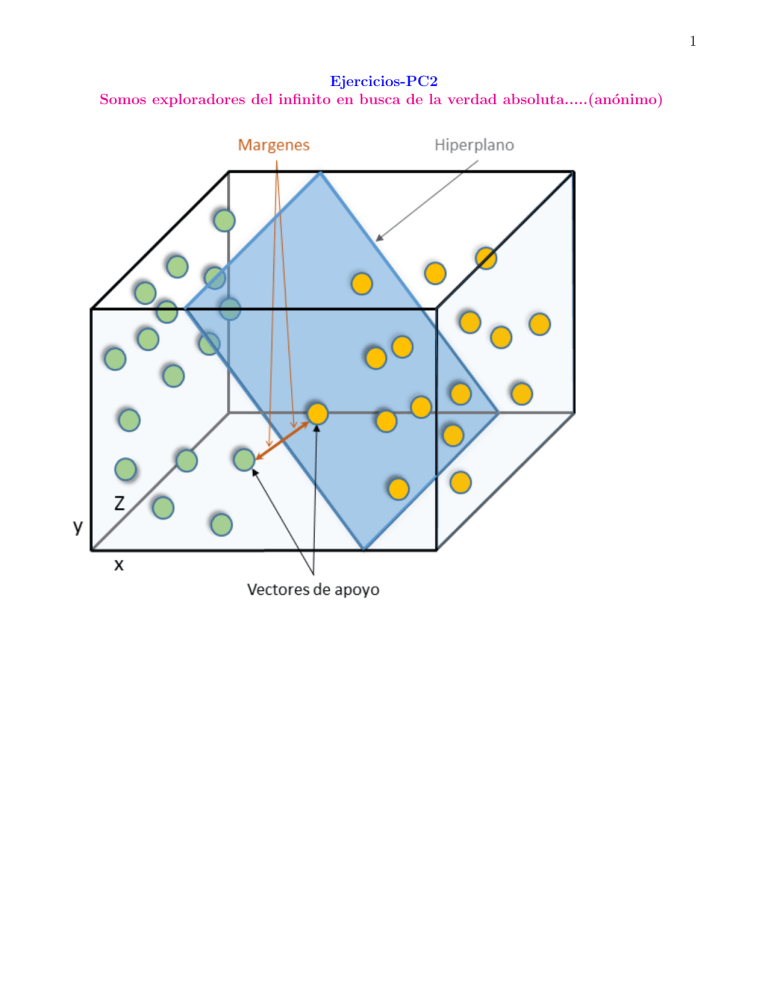
1 Ejercicios-PC2 Somos exploradores del infinito en busca de la verdad absoluta.....(anónimo) 2 0.1. Prueba de hipótesis - PC2 1. Prueba de hipótesis para la media - video de repaso link: https://www.youtube.com/watch? v=eNd8-yiS7z4 2. Prueba de hipótesis para la diferencias de medias- video de repaso link: https://www. youtube.com/watch?v=L7XkvBL7kI4 3. Prueba de hipótesis para la proporción - video de repaso link: https://www.youtube.com/ watch?v=n9jPOKjBmVE 4. Prueba de hipótesis para la diferencia de proporciones- video de repaso link: https://www. youtube.com/watch?v=Tudh7KUWFKw 5. Prueba de hipótesis para la varianza- video de repaso link: https://www.youtube.com/ watch?v=sGyfYYt1Kcs Ejercicios de S03; S04;S05;S06;S07 y S08 link : https://canvas.utp.edu.pe/courses/262461 1. Por estudios previos, se sabe que el nivel colesterol promedio de pacientes con problemas cardiacos es de 300. Un cientı́fico tiene la hipótesis de que el nivel es mayor. Por lo tanto utiliza la siguiente evidencia empı́rica. 310,202,303,311,331,200,300,301,290,300.Existirá suficiente evidencia estadı́stica que respalde la afirmación del cientı́fico con un nivel de significancia de 1 %. Solución 0.1. PRUEBA DE HIPÓTESIS - PC2 3 a) Inf ormación x̄ = 284,4 S = 45,44 n = 10 α = 0,01 =⇒ nivel de signif icancia b) P lanteamiento de hipótesis Hipotesis = H0 : µ = 300 H1 : µ > 300 c) El estadı́stico de prueba Tc = X̄ − µ √S n ⇒ Tc = 284,4 − 300 45,44 √ 10 = −1,08 Tc = −1,08 d) Región crı́tica para α = 0,01 dado T(1−α,n−1) = T(1−0,01,10−1) = 2,82 La tabla T en link https://canvas.utp.edu.pe/courses/262461/files/92194067?module_item_id=35839555 T(0,99;9) = 2,82 ⇒ La región de rechazo =⇒ h2,82; ∞i 4 Solución −1,08 6∈ h2,82; ∞i e) Conclusión: NO EXISTE SUFICIENTE EVIDENCIA ESTADISTICA PARA RESPALDAR LA AFIRMACION DEL CIENTIFICO CON UN NIVEL DE SIGNIFICANCIA DEL 1 %(completar la interpretación según el enunciado) 2. En dos plantas de una misma empresa se emplean técnicas diferentes para producir un compuesto quı́mico. Estamos interesados en la cantidad de impurezas que se generan por ambas técnicas, En la primera planta se toman 30 muestras con una media de 4.5 g/L de impurezas y una desviación tı́pica de 2. En la otra, con 30 muestras se obtiene un promedio de 3.8 y una desviación estimada de 1.3. Son equivalentes los procesos?, con un nivel de significancia de 1 %. Solución a) Inf ormación P rimera − P lanta = Segunda − P lanta = X̄1 = 4,5 S1 = 2 n1 = 30 X̄2 = 3,8 S2 = 1,3 n2 = 30 b) P lanteamiento de hipótesis Hipótesis = H0 : µ1 = µ2 H1 : µ1 6= µ2 c) El estadı́stico de prueba Zc = (4,5 − 3,8) − 0 0,7 X̄1 − X2 − (µ¯1 − µ2 ) q 2 = q = = 1,605 2 2 2 S1 S2 0,436 1,3 2 + + 30 30 n1 n2 0.1. PRUEBA DE HIPÓTESIS - PC2 5 Zc = 1,605 d) Region de aceptación para α = 0,01 dado ⇒ Z( α2 ) = Z( 0,01 ) = Z0,005 = −2,578 2 La tabla Z en link https://canvas.utp.edu.pe/courses/262461/files/92194063?module_item_id=35839557 ⇒ Z(1− α2 ) = Z(1− 0,01 ) = Z0,995 = 2,578 2 ⇒ La región de aceptación =⇒ [−2,578; 2,578] Solución 1,605 ∈ [−2,578; 2,578] e) Conclusión: NO EXISTE SUFICIENTE EVIDENCIA ESTADISTICA PARA AFIRMAR QUE LOS 2 PROCESOS DIFIEREN EN LA GENERACION DE IMPUREZAS CON UN NIVEL DE SIGNIFICANCIA DEL 1 % 3. De una muestra aleatoria de 900 ciudadanos entrevistados en Lima Metropolitana, 770 indicaron que hay problemas de seguridad ¿Indica esta evidencia que más del 85 % de los ciudadanos limeños perciben que hay problemas de seguridad?. Use el nivel de significación de 0.05 Solución a) Inf ormación X = 770 6 n = 900 p= X n = 770 900 = 0,86 ⇒ p = 0,86 α = 0,05 =⇒ nivel de signif icancia b) P lanteamiento de hipótesis Hipotesis = H0 : π ≤ 0,85 H1 : π > 0,85 c) El estadı́stico de prueba p−π Zc = q π(1−π) n 0,86 − 0,85 ⇒ Zc = q = 0,83 0,85(1−0,85) 900 Zc = 0,83 d) Región crı́tica para α = 0,05 dado Z(1−α) = Z(1−0,05) = 1,645 La tabla Z en link https://canvas.utp.edu.pe/courses/262461/files/92194063?module_item_id=35839557 Z(0,95) = 1,645 ⇒ La región de rechazo =⇒ h1,645; ∞i Solución 0,83 6∈ h1,645; ∞i 0.1. PRUEBA DE HIPÓTESIS - PC2 7 e) Conclusión: NO HAY SUFICIENTE EVIDENCIA ESTADISTICA PARA AFIRMAR QUE MAS DEL 85 % DE LOS CUIDADANOS PERCIBEN PROBLEMAS DE SEGURIDAD CON UN NIVEL DE SIGNIFICANCIA DEL 1 %(completar la interpretación según el enunciado) 4. Considere el caso de una compañı́a que fabrica productos medicinales y que está probando dos nuevos compuestos destinados a reducir los niveles de presión sanguı́nea. Los compuestos se administran a dos conjuntos de animales de laboratorio En el grupo uno, 270 de 400 animales respondieron a la droga 1 con niveles menores de presión arterial. En el grupo dos, 150 de 390 animales respondieron a la droga 2 con menores niveles de presión sanguı́nea. La compañı́a desea probar a un nivel de significancia de 0.05; si existe una diferencia en la eficacia de las dos medicinas. Solución a) Inf ormación Droga1 = Droga2 = X1 = 270 n1 = 400 p1 = Xn = 270 400 = 0,675 ⇒ p1 = 0,675 X2 = 150 n2 = 390 p2 = Xn = 150 390 = 0,385 ⇒ p2 = 0,385 p̄ = 270 + 150 = 0,53 400 + 390 ⇒ p̄ = 0,53 b) P lanteamiento de hipótesis Hipótesis = H0 : π1 = π2 H1 : π1 6= π2 8 c) El estadı́stico de prueba 0,675 − 0,385 − (0) p1 − p2 − (π1 − π2 ) =q = 233,87 = 233,87 Zc = q 1 1 p̄(1 − p̄)( n11 + n12 ) 0,53(1 − 0,53)( 400 + 390 ) Zc = 233,87 d) Region de rechazo para α = 0,05 dado bilateral (dos colitas) ⇒ Z( α2 ) = Z( 0,05 ) = Z0,025 = −1,96 2 ⇒ Z(1− α2 ) = Z(1− 0,05 ) = Z0,975 = 1,96 2 La tabla Z en link ⇒ https://canvas.utp.edu.pe/courses/262461/files/92194063?module_item_ id=35839557 ⇒ Z(1− α2 ) = Z(1− 0,01 ) = Z0,995 = 2,578 2 ⇒ La región de rechazo =⇒ h−∞; −1,96i ∪ h1,96; +∞i Solución 233,87 ∈ h−∞; −1,96i ∪ h1,96; +∞i e) Conclusión: A un nivel de significación del 5 %, existe suficiente evidencia estadı́stica para rechazar la hipótesis nula. Si existe una diferencia en la eficacia de las dos medicinas 0.1. PRUEBA DE HIPÓTESIS - PC2 9 5. La gerencia de una empresa avı́cola considera que la variabilidad que se presenta en el peso de los pollos de 3 meses es aceptable, puesto que cree que la desviación estándar de los pesos es de 250 gramos. Un grupo de socios de la empresa pone en duda lo manifestado por la gerencia y considera que la variabilidad es superior, por lo cual 6 meses después, la gerencia ordena tomar una muestra de 30 pollos de 3 meses seleccionados aleatoriamente y encuentra que la desviación estándar de la misma es de S= 225 gramos. Con un nivel de significación del 5 % compruebe quien tiene la razón Solución a) Inf ormación σ = 250g S = 225g n = 30 α = 0,05 b) P lanteamiento de hipótesis Hipotesis = H0 : σ 2 = 62500 H1 : σ 2 > 62500 c) El estadı́stico de prueba χ2c = (n − 1)S 2 (30 − 1)(225)2 = = 23,49 σ02 62500 χ2c = 23,49 d) Region crı́tica para α = 0,05 dado χ2(1−α,n−1) = χ2(1−0,05;30−1) = χ2(0,95,29) = 42,557 =⇒ χ2(1− α ,n−1) = 42,557 2 La tabla χ2 en link 10 https://canvas.utp.edu.pe/courses/262461/files/92194069?module_item_id=35839553 ⇒ La región de rechazo =⇒ h42,557; +∞i Solución 23,49 6∈ h42,557; +∞i e) Conclusión: A un nivel de significación del 5 %, no existe suficiente evidencia estadı́stica para rechazar la hipótesis nula. Por lo tanto no hay razón para dudar de la gerencia en relacion a la variabilidad que se presenta en el pesos de los pollos