Sesión de Aprendizaje: Patrones Aditivos en Matemáticas
Anuncio
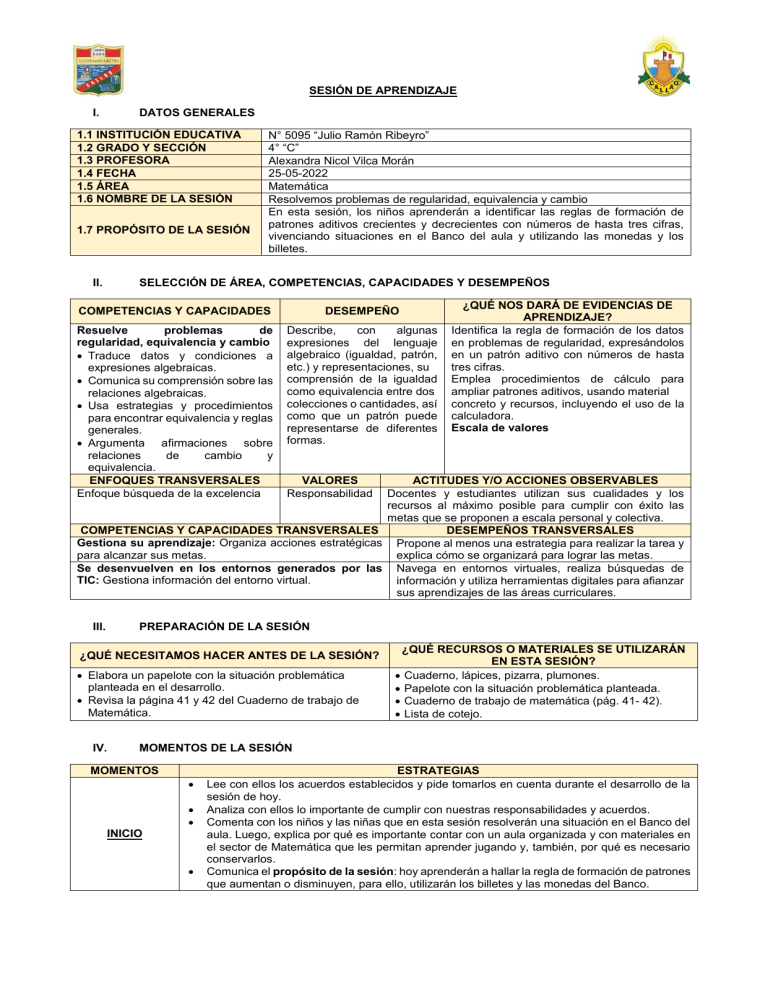
SESIÓN DE APRENDIZAJE I. DATOS GENERALES 1.1 INSTITUCIÓN EDUCATIVA 1.2 GRADO Y SECCIÓN 1.3 PROFESORA 1.4 FECHA 1.5 ÁREA 1.6 NOMBRE DE LA SESIÓN 1.7 PROPÓSITO DE LA SESIÓN II. N° 5095 “Julio Ramón Ribeyro” 4° “C” Alexandra Nicol Vilca Morán 25-05-2022 Matemática Resolvemos problemas de regularidad, equivalencia y cambio En esta sesión, los niños aprenderán a identificar las reglas de formación de patrones aditivos crecientes y decrecientes con números de hasta tres cifras, vivenciando situaciones en el Banco del aula y utilizando las monedas y los billetes. SELECCIÓN DE ÁREA, COMPETENCIAS, CAPACIDADES Y DESEMPEÑOS COMPETENCIAS Y CAPACIDADES DESEMPEÑO Resuelve problemas de regularidad, equivalencia y cambio Traduce datos y condiciones a expresiones algebraicas. Comunica su comprensión sobre las relaciones algebraicas. Usa estrategias y procedimientos para encontrar equivalencia y reglas generales. Argumenta afirmaciones sobre relaciones de cambio y equivalencia. ENFOQUES TRANSVERSALES Enfoque búsqueda de la excelencia Describe, con algunas expresiones del lenguaje algebraico (igualdad, patrón, etc.) y representaciones, su comprensión de la igualdad como equivalencia entre dos colecciones o cantidades, así como que un patrón puede representarse de diferentes formas. ¿QUÉ NOS DARÁ DE EVIDENCIAS DE APRENDIZAJE? Identifica la regla de formación de los datos en problemas de regularidad, expresándolos en un patrón aditivo con números de hasta tres cifras. Emplea procedimientos de cálculo para ampliar patrones aditivos, usando material concreto y recursos, incluyendo el uso de la calculadora. Escala de valores ACTITUDES Y/O ACCIONES OBSERVABLES Docentes y estudiantes utilizan sus cualidades y los recursos al máximo posible para cumplir con éxito las metas que se proponen a escala personal y colectiva. COMPETENCIAS Y CAPACIDADES TRANSVERSALES DESEMPEÑOS TRANSVERSALES Gestiona su aprendizaje: Organiza acciones estratégicas Propone al menos una estrategia para realizar la tarea y para alcanzar sus metas. explica cómo se organizará para lograr las metas. Se desenvuelven en los entornos generados por las Navega en entornos virtuales, realiza búsquedas de TIC: Gestiona información del entorno virtual. información y utiliza herramientas digitales para afianzar sus aprendizajes de las áreas curriculares. III. VALORES Responsabilidad PREPARACIÓN DE LA SESIÓN ¿QUÉ NECESITAMOS HACER ANTES DE LA SESIÓN? Elabora un papelote con la situación problemática planteada en el desarrollo. Revisa la página 41 y 42 del Cuaderno de trabajo de Matemática. IV. ¿QUÉ RECURSOS O MATERIALES SE UTILIZARÁN EN ESTA SESIÓN? Cuaderno, lápices, pizarra, plumones. Papelote con la situación problemática planteada. Cuaderno de trabajo de matemática (pág. 41- 42). Lista de cotejo. MOMENTOS DE LA SESIÓN MOMENTOS INICIO ESTRATEGIAS Lee con ellos los acuerdos establecidos y pide tomarlos en cuenta durante el desarrollo de la sesión de hoy. Analiza con ellos lo importante de cumplir con nuestras responsabilidades y acuerdos. Comenta con los niños y las niñas que en esta sesión resolverán una situación en el Banco del aula. Luego, explica por qué es importante contar con un aula organizada y con materiales en el sector de Matemática que les permitan aprender jugando y, también, por qué es necesario conservarlos. Comunica el propósito de la sesión: hoy aprenderán a hallar la regla de formación de patrones que aumentan o disminuyen, para ello, utilizarán los billetes y las monedas del Banco. Recoge los saberes previos sobre patrones aditivos a través de las siguientes preguntas: ¿cuándo un patrón crece o aumenta?, ¿qué ejemplo podrían mencionar?; ¿cuándo un patrón decrece o disminuye?, ¿qué ejemplo podrían mencionar? Pega en la pizarra el papelote que preparaste con la situación problemática y pide a los estudiantes que la lean atentamente: El día lunes, un comerciante retiró del banco S/.800 para pagarle a un empleado. Ese mismo día, después de pagarle, contó su dinero y le quedaron S/.775. El martes volvió a pagarle, y le quedaron S/.750. El miércoles hizo lo mismo, y le quedaron S/.725. ¿Cuánto dinero paga diariamente el comerciante a su empleado? Después de pagarle el día sábado, ¿cuánto dinero le quedará? Asegura la comprensión de la situación mediante algunas preguntas: ¿de qué trata?, ¿qué se nos pide?, etc. Solicita que algunos estudiantes expliquen a sus compañeros la situación a resolver. Ayúdalos a hallar relaciones entre los datos. Pregunta, por ejemplo: ¿cuánto dinero retiró del banco el comerciante?, ¿qué hizo con el dinero?; ¿qué pasa con el dinero a medida que transcurren los días?, ¿aumenta o disminuye?, ¿por qué? Una vez que todos hayan comprendido la situación problemática, plantea estas interrogantes: ¿alguna vez han resuelto una situación similar?, ¿cuál?, ¿cómo la resolvieron? Pregunta a los niños y a las niñas: ¿qué materiales nos pueden ser útiles para solucionar la situación?, ¿cómo los usarían? De ser necesario, oriéntalos para que elijan utilizar los materiales del Banco. Pide que se organicen en equipos a fin de vivenciar la situación y distribuirse los roles: uno será el cajero, otro el comerciante y los demás representarán al empleado. Indica que, si desean, pueden leer nuevamente el papelote. PROCESO Solicita que los equipos comuniquen sus respuestas. Luego, pregúntales si existe otra forma de encontrar la solución y comenta que no siempre podrán utilizar la vivenciación para resolver situaciones de este tipo. Rétalos a hacerlo de otra manera. Valora los aprendizajes de los estudiantes usando la lista de cotejo. Orienta a los estudiantes para que descubran la regla de formación. Utiliza la pizarra a fin de formalizar el aprendizaje de patrones aditivos. Puedes formular estas preguntas: ¿la secuencia aumenta o disminuye?, ¿en cuánto cada vez? Propón la siguiente situación problemática: Un comerciante tiene en el banco S/. 280 y ha decidido depositar cada mes la misma cantidad. En el mes de marzo, tendrá S/. 370; en abril, S/. 460; en mayo, S/. 550. ¿Cuánto tendrá ahorrado en noviembre? ¿Cuánto habrá depositado mensualmente? Invita a los niños y a las niñas a solucionar la situación aplicando la estrategia que ellos crean conveniente y con los recursos que les convenga. Cuando todos hayan terminado, pide que escriban las conclusiones en su cuaderno y, si lo consideras pertinente, plantea estas preguntas: ¿cómo es un patrón creciente?, ¿cómo es un patrón decreciente?, ¿qué es una regla de formación? Un patrón es aditivo cuando se suma o resta una misma cantidad. Un patrón aditivo es creciente cuando se suma, aumenta o crece. La regla de formación es el número que se suma o aumenta. *Registrar el logro de aprendizajes de los estudiantes en una lista de cotejo. PLANTEA OTRAS SITUACIONES: Resolvemos actividades sugeridas de las páginas 41 y 42 del cuaderno de trabajo de matemática 4° grado. CIERRE Reflexionamos lo aprendido. Realizar las siguientes interrogantes. ¿Les gustó lo que hicieron?, ¿por qué? ¿qué aprendieron hoy? ¿alguien me puede recordar qué es un patrón aditivo? ¿tuvieron dificultades?¿cuáles?, ¿cómo las superaron? ¿para qué les servirá lo aprendido? N° 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 Nombre y apellidos de los estudiantes Explica sus resultados y procedimientos al continuar un patrón aditivo de hasta tres cifras. Emplea procedimientos de cálculo para ampliar patrones aditivos, usando material concreto y recursos, incluyendo el uso de la calculadora. Identifica la regla de formación de los datos en problemas de regularidad, expresándolos en un patrón aditivo con números de hasta tres cifras. Anexo: Lista de cotejo