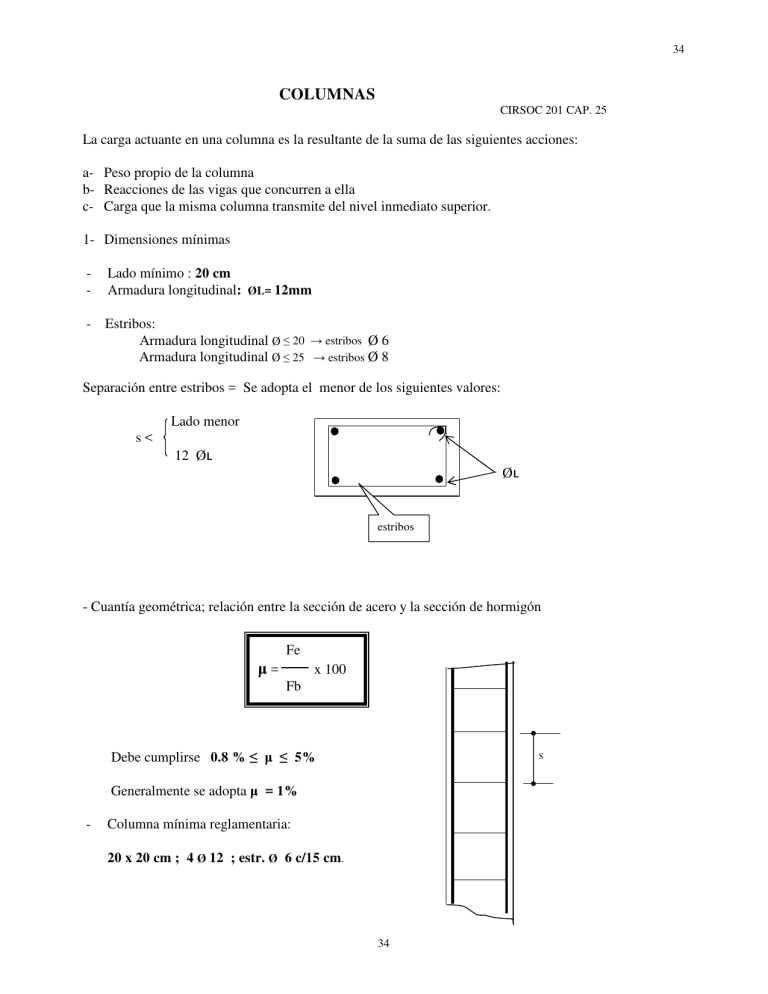
34 COLUMNAS CIRSOC 201 CAP. 25 La carga actuante en una columna es la resultante de la suma de las siguientes acciones: a- Peso propio de la columna b- Reacciones de las vigas que concurren a ella c- Carga que la misma columna transmite del nivel inmediato superior. 1- Dimensiones mínimas - Lado mínimo : 20 cm Armadura longitudinal: ØL= 12mm - Estribos: Armadura longitudinal Ø ≤ 20 → estribos Ø 6 Armadura longitudinal Ø ≤ 25 → estribos Ø 8 Separación entre estribos = Se adopta el menor de los siguientes valores: Lado menor s< 12 Øȯ Øȯ Øȯ estribos - Cuantía geométrica; relación entre la sección de acero y la sección de hormigón Fe µ= x 100 Fb s Debe cumplirse 0.8 % ≤ µ ≤ 5% Generalmente se adopta µ = 1% - Columna mínima reglamentaria: 20 x 20 cm ; 4 Ø 12 ; estr. Ø 6 c/15 cm. 34 35 2- ESBELTEZ Este concepto está asociado a la forma que tiene un objeto. No se duda en definir como esbelto aquello que es mucho más alto que ancho ( Ej. Una columna de alumbrado), inversamente decimos poco esbelta a la figura que es casi tan ancha como alta. ( ej. Barril, columna de P.B. de un edificio de 15 pisos ). . Podemos definir a la esbeltez como la relación entre la altura y la sección transversal del elemento analizado, estando representada la sección transversal por su radio de giro. Lp Lp: longitud de pandeo i: radio de giro: √J/A A; área de la sección J: momento de inercia λ= i Para secciones cuadradas o rectangulares Para secciones circulares i = 0.29b i =0.25d b: lado menor d: diámetro En el caso de las piezas comprimidas tiene fundamental importancia esta relación pues esta latente el peligro que las mismas se deformen lateralmente, fenómeno denominado PANDEO. La capacidad de soportar cargas disminuye a medida que aumenta la esbeltez. 3- LONGITUD DE PANDEO : Sk Para el caso de columnas la longitud de pandeo depende de las condiciones de vínculos de la misma. Se adopta como la distancia entre los puntos de inflexión de la pieza deformada: Sk = K .L Sk Sk Sk Sk K=1 K= 0.7 K= 0.5 K= 2 Para columnas de pórticos ver del Bibliografía Estructuras de Hormigón Armado Ing Leonhardt En general, para estructuras de edificios las normas aconsejan adoptar como longitud de pandeo la distancia entre piso y piso sin empotramientos. K=1 . 4- DIMENSIONADO . Metodo Formula de dimensionado: (1) N.ν. ω .ω = Fb . βr + fe . βs 35 N: carga actuante ν: coef. seguridad mínimo 2.1 ω: coef. de pandeo Fb: sección de hormigón fe: sección de acero βr / βs: Tensiones de cálculo de hormigón y acero. 36 El coeficiente de pandeo ω se obtiene en función de la esbeltez. Para columnas cuadradas y rectangulares: λ= Sk / b b= lado menor λ= Sk / i i = radio de giro Tabla n° 7 Para cualquier sección: En la formula (1) vemos que hay dos incógnitas: sección de hormigón y sección de acero, por lo tanto es necesario adoptar una y despejar la otra. En función de la cuantía la expresión queda: (2) N.ν. ω = Fb . ( βr + µ . βs) 5- PREDIMENSIONADO A efectos de obtener la sección de hormigón se utiliza una tensión de trabajo σ’b = El área necesaria será σ’bk /2 N (kg) Fb = σ’b (kg/cm²) Con este valor usamos (1) y obtenemos fe. 6- EJEMPLOS 6.1- Datos N = 39 tn. Hormigón H-17 Sk= 4,00 m Acero ADN 420. 39000 kg Predimensionado Fb = = 459 cm² → b= √Fb= 21 cm adoptamos 20x20cm 85 kg/cm² Esbeltez de (1) λ = 400/20 = 20 N.ν. ω tabla n°7 - Fb . βr fe = ω = 1.08 39000kg 2,1 1,02 – 20cm 20cm 140 kg/cm² = = 7,70 cm² 4200 kg/cm² βs adoptamos Estribos Ø 6 4 Ø 16 (8.04 cm²) separación 12 Ø = 12 x 1,6 cm = 19 cm . 36 estribos Ø 6 c/19 cm. 37 Verificación de cuantía: µ = 100 fe / fb = 100 8.04 cm²/ 400 cm²= 2.00 % verifica 6.2 - Datos: N= 45 tn. H-17 ; ADN 420 Sk= 3,50m Se adopta una cuantía del 1% y tomamos N.ν ω ω =1 45000kg . 2,1 . 1,00 de (2) Fb= = βr + µ . βs = 519 cm² ( 140 kg/cm² + 0,01 . 4200 kg/cm² ) b=√Fb=√519 ≅ 23cm. Adopto columna de 23 x 23 cm Sección necesaria de acero: fe= µ . fb = 0.01 . 23 . 23 = 5,29 cm² → 6 Ø 12 (6.78cm2) estribos: Ø 6 c/15 Verificación de esbeltez: ω = 1.00 λ= 350/23 = 15,20 igual al adoptado En caso de no verificar deberá redimensionarse con este nuevo valor de ω 6.3 - Calcular la carga máxima que admite la siguiente columna: Sección 30 x 30 cm - fe = 8 Ø 16 λ= 600/30 - Sk= 6,00m - H-21 - ADN-420 ω = 1,08 = 20 Fb . βr + fe . βs (1) N = ω .ν 30 cm x 30cm x 175 kg/cm² + 16,08 x 4200 kg/cm² = = 99.222 kg 1,08 2,1 37