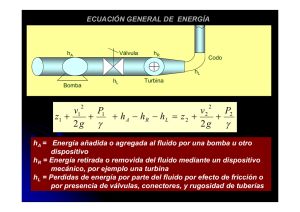
GUIA DE PRACTICA Nº 3 PERDIDAS DE CARGA EN TUBERIAS FLUJO INTERNO 1. OBJETIVOS: OBJETIVO GENERAL : Evaluar las perdidas secundarias en un fluido en flujo interno a través de un conjunto de tuberías y accesorios en función de la caída de presión. OBJETIVOS ESPECIFICOS : Determinar las perdidas locales o secundarias dentro de codos de 90º, contracciones , ensanchamientos e inglete dentro de un banco de tuberías. Calcular el margen de error entre la constante del accesorio calculado experimentalmente y el teórico. Conocer la simbología de redes de flujo interno. 2. FUNDAMENTO TEORICO : Los fluidos en movimiento o flujo interno forman parte básica para la producción de servicios dentro de las actividades industriales , residenciales y comerciales. Al Ingeniero en Energía le compete el tratamiento adecuado de la conducción de flujos bajo conceptos de optimización económica, técnica, ambiental y de estética. La aplicación de la Ecuación de Bernoulli para fluidos reales , entre 2 secciones de un mismo tramo de tubería es : Donde : Donde : hfp = es la sumatoria de perdidas primarias o longitudinales. hfs = Perdidas secundarias o, locales por accesorios. Al hablar de perdidas en tuberías, lleva a estudiar los flujos internos que sean completamente limitados por superficies sólidas con un grado de rugosidad según el material del cual están fabricadas. Este flujo es muy importante de analizar ya que permitirá diseñar las redes de tuberías y sus accesorios más óptimos. Las pérdidas de energía que sufre una corriente cuando circula a través de un circuito hidráulico se deben fundamentalmente a : Variaciones de energía potencial del fluido. Variaciones de energía cinética. Rozamiento o fricción. PERDIDAS PRIMARIAS : Llamadas perdidas longitudinales o pérdidas por fricción , son ocasionadas por la fricción del fluido sobre las paredes del ducto y se manifiestan con una caída de presión. Empíricamente se evalúa con la formula de DARCY - WEISBACH: Donde : L = longitud de la tubería. D = Diámetro de la tubería. V = velocidad media del flujo. f = factor de fricción de la tubería. De donde el factor de fricción de la tubería depende del Número de Reynolds ( Re ) y de la rugosidad relativa ( ε / D ) . Para esto se hace uso del Diagrama de Moody. Básicamente las Pérdidas primarias son directamente proporcionales a la longitud de la tubería. PERDIDAS SECUNDARIAS : También conocidas como perdidas locales o puntuales , las cuales son originadas por una infinidad de accesorios que se ubican dentro de un sistema de tuberías , como por ejemplo : Válvulas. Codos. Niples. Reducciones. Ensanchamientos. Uniones universales. Etc. La expresión para evaluar las perdidas secundarias ( en metros de columna del fluido) es la siguiente : Donde K es la constante para cada accesorio y depende del tipo de accesorio , material y diámetro. Luego la longitud equivalente será : La longitud equivalente se puede hallar en manuales y libros. En el equipo FME-05 de pérdidas de carga local estudia las pérdidas de energía cinética de un fluido que circula por una tubería. Estas se deben principalmente a variaciones bruscas de velocidad causadas por : Cambios bruscos de sección. Perturbación del flujo normal de la corriente , debido a cambios de dirección provocadas por la existencia de un codo , curva , etc. Rozamiento o fricción. Las pérdidas de carga que sufre un fluido al atravesar todos los elementos expresada en metros del fluido , puede calcularse con la siguiente expresión : Donde : K = coeficiente de pérdidas de carga. V= velocidad del fluido. ∆h = diferencia de altura manométrica. g= gravedad. ENSANCHAMIENTO SUBITO : Al fluir un fluido de un conducto de menor a uno mayor a través de una dilatación súbita, su velocidad disminuye abruptamente, ocasionando una turbulencia que genera una pérdida de energía. La cantidad de turbulencia, y por consiguiente, la cantidad de pérdida de energía, depende del cociente de los tamaños de los dos conductos. La perdida menor se calcula de la ecuación: Donde v1 es la velocidad de flujo promedio en el conducto menor que está delante de la dilatación. Al hacer ciertas suposiciones de simplificación respecto del carácter de la corriente de flujo al expandirse a través de una dilatación súbita, es posible predecir analíticamente el valor de k a partir de la siguiente ecuación: = FUENTE: Robert L.Mott.1996.Mecanica de Fluidos Aplicada. 4 ed. México: Prentice Hall ENSANCHAMIENTO GRADUAL : Si la transición de un conducto menor a uno mayor puede hacerse menos abrupta que la dilatación súbita de bordes cuadrados, la perdida de energía se reduce. Esto normalmente se hace colocando una sección cónica entre los dos conductos, como se muestra en la siguiente figura. Las paredes en pendiente del cono tienden a guiar el fluido la desaceleración y expansión de la corriente de flujo. FUENTE: Robert L.Mott.1996.Mecanica de Fluidos Aplicada. 4 ed. México: Prentice Hall La pérdida de energía para una dilatación gradual se calcula a partir de: Donde v1 es la velocidad del conducto menor que está delante de la dilatación. La magnitud de K depende tanto de la proporción de diámetro D2 / D1 como del ángulo de cono, θ y D2 / D1. Ver en el Texto : King, H.W y E.F. Brater, 1963 Handbook of Hydraulics, 5º ed. Nueva York: McGraw-Hill la TABLA DE COEFICIENTE DE RESISTENCIA CONTRACCION SUBITA : La pérdida de energía debido a una contracción súbita, como la esbozada en la figura se calcula a partir de: Donde v2 es la velocidad en la corriente hacia abajo del conducto menor a partir de la contracción. El coeficiente de resistencia K depende de la proporción de los tamaños de los dos conductos y de la velocidad de flujo, como se muestra en la figura. FUENTE: Robert L.Mott.1996.Mecanica de Fluidos Aplicada. 4 ed. México: Prentice Hall CONTRACCION GRADUAL : La pérdida de energía en una contracción puede disminuirse sustancialmente haciendo la contracción más gradual. La figura muestra una contracción de este tipo, formada mediante una sección cónica entre los dos diámetros con cambios abruptos en las junturas. El ángulo Ѳ se denomina ángulo de cono. FUENTE: Robert L.Mott.1996.Mecanica de Fluidos Aplicada. 4 ed. México: Prentice Hall COEFICIENTE DE RESISTENCIA PARA JUNTAS Y VALVULAS : Se dispone de muchos tipos diferentes de válvulas y juntura de varios fabricantes para especificaciones e instalación en sistemas de flujo de fluido. Las válvulas se utilizan para controlar la cantidad de flujo y pueden ser válvulas de globo, de ángulo, de mariposa, otros varios tipos de válvula de verificación y mucha más. El método para determinar el coeficiente de resistencia k es diferente. El valor de k se reporta en la forma: El valor de , llamado la proporción de longitud equivalente, se reporta en la siguiente tabla y se considera que es una constante para un tipo dado de válvula o juntura. El valor de mismo se denomina la longitud equivalente y es la longitud del conducto recto del mismo diámetro nominal como la válvula que tendría la misma resistencia que esta. El termino D es el diámetro interno real del conducto. El término es el factor de fricción en el conducto al cual está conectada la válvula o juntura, tomado en la zona de turbulencia completa. Tipo Válvula de globo – complemente abierta Válvula de ángulo – complemente abierta Válvula de compuerta – complemente abierta - ¾ abierta - ½ abierta - ¼ abierta Válvula de verificación – tipo giratorio Válvula de verificación – tipo bola Válvula de mariposa – completamente abierta Codo estándar 90º Codo de radio de largo de 90º Codo de calle de 90º Codo estándar de 45º Codo de calle de 45º Codo de devolución cerrada Te estándar – con flujo a través de un tramo Te estándar – con flujo a través de una rama Longitud equivalente En diámetros De conducto , Lc/D 340 150 8 35 160 900 100 150 45 30 20 50 16 26 50 20 60 Resistencia en Válvulas y junturas expresadas como longitud equivalente en diámetros de conducto, Lc/D Fuente: válvulas de sifón, Joliet, IL. Los valores de varían con el tamaño del conducto y de la válvula, ocasionando que el valor del coeficiente de resistencia K también varie.la siguiente tabla enumera los valores de para tamaños estándar de conductos de acero comercial, nuevo y limpio. Tamaño de conducto Nominal (pulg) ½ ¾ 1 1¼ 1½ 2 2 ½, 3 Factor de fricción, 0.027 0.025 0.023 0.022 0.021 0.019 0.018 Tamaño de conducto Nominal (pulg) 4 5 6 8-10 12-16 18-24 Factor de fricción, 0.017 0.016 0.015 0.014 0.013 0.012 Factor de Fricción en Zona de Turbulencia completa para conductos de acero comercial nuevo y limpio. FUENTE: Robert L.Mott.1996.Mecanica de Fluidos Aplicada. 4 ed. México: Prentice Hall 3. EQUIPOS Y MATERIALES: Banco Hidráulico. Equipo demostrativo para perdidas de carga FME-05. Cronometro digital. Extensión. 4. PROCEDIMIENTO EXPERIMENTAL : LLENADO DE TUBOS MANOMETRICOS : Cierre de las válvulas de suministro de agua del banco hidráulico y de descarga del equipo demostrativo. Encienda el motor de la bomba de agua del banco hidráulico y en forma progresiva abra las válvulas de suministro de agua del banco y la de descarga del equipo demostrativo para pérdidas secundarias , inundando todos los conductos del equipo , con la finalidad de eliminar las burbujas de aire. Luego de que el sistema se encuentra a presión de 0.5 Bar y libre de burbujas de aire , ir cerrando rápidamente las dos válvulas y apagar el motor de la bomba. Abrir la válvula de venteo y bombear aire hasta alcanzar los doce niveles de vidrio hasta una altura de 100 mm. De columna de agua . Ayudarse abriendo ligeramente la válvula de descarga. Cerrar hasta alcanzar una presión en el sistema de 0 Bar. PERDIDAS DE CARGA EN ACCESORIOS : Cerrar las válvulas ,dejando solo abiertas la válvula de entrada y la de salida del codo largo hacia las alturas piezometricas. Encender el motor de la bomba de agua , fijando un determinado flujo para regular el caudal , y procurando la existencia de una diferencia entre las 2 alturas piezometricas. Repetir el mismo paso con otro caudal ( 4 veces). Realizar lo mismo con cada uno de los accesorios. Secar y limpiar el Equipo de Pruebas. 5. DATOS A RECOLECTAR : Para cada accesorio : Codo Largo , codo medio , ensanchamiento, contracción, codo corto e inglete elaborar los siguientes cuadros : Volumen 5 litros 5 litros 5 litros 5 litros Tiempo (sg) hi (mmca) hs(mmca) 6. CUESTIONARIO : Para cada uno de los accesorios elaborar y llenar el siguiente cuadro : Q(m3/sg) V2(m/sg) ∆h K PROMEDIO Determinar el margen de error con el valor teórico. Graficar ∆h vs V2 Interpretar cada grafico. Investigar acerca que entidades se encargan de Normar los Sistemas Hidráulicas. Describir la Nomenclatura Técnica para distintos accesorios hidráulicos. Qué diferencia existe entre hidráulica y la óleo hidráulica.? . Se aplica las mismas ecuaciones teóricas en los diseños óleo hidráulicos. Partiendo de la ecuación de la energía y de Bernoulli , hallar la ecuación de pérdidas secundarias por una tubería horizontal.