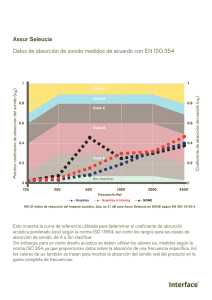
CARACTERIZACIÓN ACÚSTICA DE UN MATERIAL DE USO ALTERNATIVO A
PARTIR DE LA RESISTENCIA AL FLUJO Y EL COEFICIENTE DE ABSORCIÓN
PARA EVALUAR SU POSIBLE APLICACIÓN EN SOLUCIONES ACÚSTICAS.
ELOÍSA ARCILA FERNÁNDEZ
UNIVERSIDAD DE SAN BUENAVENTURA SECCIONAL MEDELLÍN
FACULTAD DE INGENIERÍAS
INGENIERÍA DE SONIDO
MEDELLÍN
2015
CARACTERIZACIÓN ACÚSTICA DE UN MATERIAL DE USO ALTERNATIVO A
PARTIR DE LA RESISTENCIA AL FLUJO Y EL COEFICIENTE DE ABSORCIÓN
PARA EVALUAR SU POSIBLE APLICACIÓN EN SOLUCIONES ACÚSTICAS.
ELOÍSA ARCILA FERNÁNDEZ
Proyecto presentado para optar al título de Ingeniera de sonido
Asesor
Ingeniera Diana María Garza.
UNIVERSIDAD DE SAN BUENAVENTURA SECCIONAL MEDELLÍN
FACULTAD DE INGENIERÍAS
INGENIERÍA DE SONIDO
MEDELLÍN
2015
2
DEDICATORIA
Este trabajo está dedicado a mis padres, que han sido un apoyo incondicional en
mi vida y me han brindado todo lo necesario para mi desarrollo intelectual,
espiritual y personal. Porque por ellos soy y por ellos vivo, y en cada momento
dentro de este proceso de aprendizaje fueron mi motivación para hacer las cosas
bien y obtener enseñanzas de las diferentes situaciones presentadas.
3
AGRADECIMIENTOS
Agradezco a mi padre por su contribución y compañía durante el desarrollo de
este proyecto de investigación; a mi asesora, la Ingeniera Diana María Garza por
su disposición y enseñanza, al profesor Msc. Héctor García Mayén por su
colaboración e interés, a mis compañeros incondicionales en momentos que
requerí de su ayuda, al semillero de investigación de Materiales por su
cooperación en las mediciones y a todos los profesores que accedieron a
ayudarme en las diferentes ocasiones.
4
CONTENIDO
CONTENIDO ........................................................................................................... 5
RESUMEN ............................................................................................................... 8
1. JUSTIFICACIÓN ................................................................................................. 9
2. PLANTEAMIENTO DEL PROBLEMA .............................................................. 10
3. OBJETIVO GENERAL ...................................................................................... 12
4. OBJETIVOS ESPECÍFICOS ............................................................................. 12
5. MARCO REFERENCIAL ................................................................................... 13
5.1 MARCO CONCEPTUAL ........................................................................................ 13
5.1.1 Interacción del sonido con una superficie ........................................................ 13
5.1.1.1 Absorción y coeficiente de absorción ...................................................................... 14
5.1.1.2 Impedancia Acústica ................................................................................................ 14
5.1.1.3 Reacción local y extendida ...................................................................................... 15
5.1.2 Propagación de ondas sonoras en un tubo ..................................................... 15
5.1.3 Materiales acústicos absorbentes de sonido ................................................... 16
5.1.3.1 Absorción en materiales porosos............................................................................. 16
5.1.3.1.a Absorción de una superficie plana de impedancia uniforme ............................ 17
5.1.3.1.b Modelos para materiales absorbentes de sonido. ............................................ 18
5.1.3.1.b.1 Modelo de Allard y Champoux .................................................................. 19
5.1.3.2 Características físicas de los materiales absorbentes............................................. 20
5.1.3.2.a Isotropía y homogeneidad ................................................................................ 21
5.1.3.2.b Porosidad .......................................................................................................... 21
5.1.3.2.c Tortuosidad ....................................................................................................... 21
5.1.3.2.d Resistencia al flujo de aire y resistividad al flujo. ............................................. 21
5.1.3.2.d.1 Aplicaciones del valor de resistencia al flujo en soluciones acústicas ..... 23
- Absortores de sonido usando capas delgadas .............................................................................. 23
Capas rígidas ................................................................................................................................................... 23
Capas flexibles .......................................................................................................................................... 26
- Ductos recubiertos .................................................................................................................................... 28
Diseño de silenciadores para ductos recubiertos..................................................................... 29
- Absortores Resonantes ........................................................................................................................... 31
5
Micro-perforaciones .............................................................................................................................. 31
- Otros absortores ......................................................................................................................................... 32
Mecanismo de Flujo de Energía ........................................................................................................ 32
5.1.4 Métodos de medición para la caracterización de materiales acústicos ............ 33
5.1.4.1 Tubo de Kundt o tubo de impedancia ...................................................................... 34
5.1.4.1.a ISO 10534-1 / ASTM C384 “Acústica – Determinación del coeficiente de
absorción e impedancia en tubos de impedancia. Parte 1: Método de la tasa de ondas
estacionarias” .................................................................................................................. 35
5.1.4.1.b ISO 10534-2 / ASTM E1050-12 “Acústica – Determinación del coeficiente de
absorción e impedancia en tubos de impedancia. Parte 2: Método de función de
transferencia” ................................................................................................................... 36
5.1.4.2 Método de Ingard y Dear para la medición de la resistencia específica al flujo de
aire ....................................................................................................................................... 37
5.2. ESTADO DEL ARTE ............................................................................................ 39
6. METODOLOGÍA ................................................................................................ 44
6.1 Materiales utilizados para la caracterización ..................................................... 44
Acustiplaca .............................................................................................................. 45
Frescasa .................................................................................................................. 46
Black Theater ........................................................................................................... 47
Acustifibra ................................................................................................................ 48
6.2 Medición del coeficiente de absorción por el método del tubo de onda
estacionaria ................................................................................................................ 51
6.3 Diseño y construcción del tubo de onda estacionaria para la medición de
resistencia al flujo...................................................................................................... 53
6.3.1 Pseudocódigo ................................................................................................. 58
6.4 Medición de resistencia al flujo por el método de Ingard y Dear. .................... 58
7. RESULTADOS .................................................................................................. 60
7.1 Coeficiente de absorción por el método del tubo de onda estacionaria ......... 60
7.2 Resistencia al flujo por el método de Ingard y Dear. ......................................... 62
8. ANÁLISIS DE RESULTADOS........................................................................... 64
Medición del coeficiente de absorción..................................................................... 64
Comparación del coeficiente de absorción calculado con el modelo de Allard y
6
Champoux contra los resultados de la medición del coeficiente de absorción por
el método del tubo de impedancias.......................................................................... 66
Influencia de la resistividad en el coeficiente de absorción. .................................. 70
8.1 Evaluación de la aplicación acústica del material alternativo. ......................... 71
9. CONCLUSIONES .............................................................................................. 74
10. LISTA DE TABLAS ......................................................................................... 75
11. LISTA DE FIGURAS ....................................................................................... 76
12. REFERENCIAS BIBLIOGRÁFICAS ............................................................... 78
Anexo A: Consideraciones previas a la medición del coeficiente de
absorción por el método del tubo de onda estacionaria. ................................. 81
A. 1. Medición del espectro en frecuencia dentro del tubo..................................... 81
A.2. Correcciones: Medición en terminación rígida ................................................ 82
Anexo B: Consideraciones a tener en cuenta en la medición de Resistencia
al flujo por el método de Ingard y Dear. ............................................................. 85
Anexo C: Algoritmos utilizados para el cálculo de las variables. ................... 86
C.1. Coeficiente de absorción ................................................................................... 86
C.2. Resistencia al flujo normalizada ....................................................................... 87
C.3. Impedancia característica y coeficiente de absorción a partir del valor de
Resistividad................................................................................................................ 88
Anexo D: Certificado de calibración del sonómetro 01 dB. ............................. 89
Anexo E: Ficha Técnica del material alternativo. Spacer. ................................ 91
7
RESUMEN
Los materiales utilizados en la construcción, son de gran importancia en las
soluciones acústicas, es necesario conocer su comportamiento a la hora del
diseño y la implementación, pues de ello depende la efectividad de los
acondicionamientos o las medidas de control. En este proyecto se pretende
caracterizar acústicamente materiales tradicionalmente usados en soluciones
acústicas y materiales alternativos en búsqueda de aplicaciones en dicho campo.
La caracterización se hace a partir de la resistencia al flujo y el coeficiente de
absorción. Para hacerlo, se seleccionaron los materiales a caracterizar y
posteriormente se realizó la medición del coeficiente de absorción por medio del
tubo de onda estacionaria siguiendo el estándar internacional ISO 10534. La
medición de resistencia al flujo se hizo por el método de Ingard y Dear, el cual
requería un montaje especializado que se desarrolló dentro de la investigación.
Seguidamente se evaluó la influencia de dicho valor en el coeficiente de absorción
de los materiales, y con base en esto, se comparó un material alternativo con los
materiales tradicionalmente usados y se evaluó su posible aplicación en la
realización de un panel acústico para ser implementado en ambientes
hospitalarios con el fin de disminuir el ruido generado por las voces humanas. Con
los resultados obtenidos se concluyó que el valor de resistividad o resistencia
específica al flujo por unidad de espesor, puede relacionarse con la absorción de
un material, sin embargo no describe totalmente su comportamiento; se reconoció
que el método de medición de Ingard y Dear es una alternativa de construcción
sencilla y costos reducidos para determinar la resistencia al flujo de un material; y
se determinó la importancia de este valor para una caracterización acústica de un
material.
Palabras
clave:
Caracterización,
Materiales,
Resistencia al flujo, Tubo de onda estacionaria.
8
Coeficiente
de
absorción,
1. JUSTIFICACIÓN
El crecimiento de la ciudad de Medellín ha aportado una mejor visibilidad de la
acústica y el control de ruido en los diferentes campos donde dichos temas son
relevantes, los materiales aplicables en estas disciplinas son de gran importancia
ya que en gran parte son los responsables de la efectividad de los
acondicionamientos o medidas de control.
Materiales tradicionales como la lana de roca y la fibra de vidrio son efectivos en
aplicaciones acústicas donde son utilizados como absorbentes de sonido, sin
embargo, se presentan restricciones en su aplicabilidad para ciertos lugares, como
por ejemplo los entornos hospitalarios, que requieren materiales lavables para
conservar un ambiente aséptico; es por esto que el desarrollo de nuevos
materiales puede generar un impacto positivo proporcionando nuevas alternativas
y posibilidades para su aplicación.
Dentro del desarrollo de materiales acústicos es necesario proporcionar la
información de ciertos parámetros que son importantes para su empleo, uno de
estos parámetros es el coeficiente de absorción, el cual depende de otras
variables del material como lo es la resistencia al flujo. Al tener la necesidad de
caracterizar los materiales tradicionales de una forma más completa y las pocas
opciones de materiales absorbentes disponibles que pueden ser aplicados, se
plantea entonces identificar la influencia de la resistencia al flujo en el coeficiente
de absorción y la relevancia de su valor para el cálculo de alguna medida de
control dentro alguna solución acústica para luego caracterizar un material
alternativo a partir de dichos valores y analizar su posible aplicación en soluciones
acústicas.
9
2. PLANTEAMIENTO DEL PROBLEMA
¿Es posible caracterizar un material de uso alternativo a partir de los valores de
resistencia al flujo y coeficiente de absorción para analizar su posible aplicación en
soluciones acústicas?
La caracterización acústica de los materiales proporciona facilidad al momento de
implementarlos
en
diferentes
aplicaciones,
una
caracterización
completa
suministra más posibilidades en su empleo, pues al tener más información, las
alternativas de su uso son mayores. Las empresas desarrolladoras de materiales
absorbentes proporcionan información de unos pocos parámetros, entre ellos el
coeficiente de absorción, el cual determina la cantidad de energía sonora que el
material puede absorber con respecto a la energía que incide, sin embargo hay
otros parámetros que son importantes para la caracterización, ya sea por su
influencia en el coeficiente de absorción o porque su valor puede ser relevante
para el cálculo de alguna medida de control dentro de la solución acústica, uno de
estos parámetros es la resistencia al flujo, que es una de las características que
posee un material absorbente, ésta, junto al coeficiente de absorción, pueden
obtenerse a partir de mediciones estandarizadas para incidencia normal como lo
es la ISO 10534-1 / ASTM C384 “Acústica – Determinación del coeficiente de
absorción e impedancia en tubos de impedancia. Parte 1 – 2 para el coeficiente de
absorción, y la UNE EN ISO 29053:1994 para la resistencia al flujo, ambas
cuentan con la necesidad equipos especializados, que para el caso de la UNE EN
ISO 29053:1994 no se disponen, sin embargo existen métodos alternativos como
el propuesto por Ingard y Dear para obtener el valor de resistencia al flujo de una
forma más simple.
Conociendo la necesidad de caracterizar de manera más completa los materiales
tradicionales y las pocas opciones de materiales absorbentes disponibles que
10
puedan ser aplicados en diferentes situaciones, se plantea entonces caracterizar
un material de uso alternativo a partir de los valores de resistencia al flujo y
coeficiente de absorción para analizar su posible aplicación en soluciones
acústicas, haciendo uso del método de Ingard y Dear para obtener valores de
resistencia al flujo, y la ISO 10534-1 / ASTM C384 para el coeficiente de absorción
a incidencia normal.
11
3. OBJETIVO GENERAL
Caracterizar un material de uso alternativo a partir de los valores de resistencia al
flujo de aire y coeficiente de absorción del sonido y analizar si representa una
opción diferente para las soluciones acústicas, comparando los resultados de las
mediciones del nuevo material contra los valores adquiridos de los materiales
absorbentes tradicionales del mercado.
4. OBJETIVOS ESPECÍFICOS
Seleccionar el material a caracterizar entre las opciones disponibles para
uso alternativo teniendo en cuenta las características físicas necesarias
para la absorción del sonido.
Realizar mediciones del coeficiente de absorción por el método del tubo de
onda estacionaria según la ISO 10534-1 / ASTM C384 “Acústica –
Determinación del coeficiente de absorción e impedancia en tubos de
impedancia - Parte 1.
Desarrollar el montaje y la medición de la resistencia al flujo de aire por el
método de Ingard y Dear.
Determinar la influencia que tiene la resistencia al flujo en el coeficiente de
absorción de un material por medio de la comparación de los resultados de
las mediciones realizadas.
Determinar posibles aplicaciones acústicas del material alternativo.
12
5. MARCO REFERENCIAL
5.1 MARCO CONCEPTUAL
5.1.1 Interacción del sonido con una superficie
Cuando una onda sonora interactúa con la superficie de un material, la energía
que contiene la onda incidente se refleja, se absorbe y se transmite a través del
material (Figura 1) [1].
(1)
Figura 1. Interacción de ondas sonoras con una superficie [1].
donde
es la energía que incide a las superficie,
la energía absorbida y
es la energía reflejada,
es
es la energía transmitida. En el análisis que involucra
solo la interacción de una onda sonora con el material, la diferencia entre
absorción, y transmisión, no es relevante [1], si se divide la ecuación 1 por la
energía incidente, se logran definir los términos de coeficiente de absorción y
coeficiente de reflexión.
(2)
donde
es la suma de la energía absorbida y transmitida a través del material.
.
13
5.1.1.1 Absorción y coeficiente de absorción
La absorción es la disipación de la energía sonora, se define también como la
propiedad que poseen los materiales de convertir dicha energía en calor [2]. Es
posible definir entonces el coeficiente de absorción como la razón de la energía
absorbida o transmitida con la energía incidente sobre una superficie (Ecuación 3)
[3]
(3)
y el coeficiente de reflexión como la relación entre la energía reflejada y la energía
incidente.
(4)
El coeficiente de reflexión también puede expresarse en términos del coeficiente
de reflexión complejo | | [1].
| |
(5)
Por lo que reemplazando las ecuaciones (3), (4) y (5) en la ecuación (1), el
coeficiente de absorción es
| |
(6)
Dicho coeficiente es usado para calificar la efectividad de un material al absorber
sonido, varía con el ángulo de incidencia, la frecuencia y las características físicas
del material [4].
5.1.1.2 Impedancia Acústica
La impedancia acústica (Ecuación (7)) sobre una superficie es la relación compleja
de la presión acústica promedio eficaz sobre la superficie y la velocidad de
volumen efectiva a través de ella [5].
̃
[
̃
]
(7)
La impedancia acústica específica, está definida como la relación de la presión
sonora y la velocidad de partícula efectivas en un punto del medio acústico [5] [6].
14
̃
̃
[
]
Se puede expresar como un parámetro complejo, donde la parte real es la
resistencia y la parte imaginaria es la reactancia (Ecuación (8)) [7].
[
]
(8)
La impedancia característica del medio Zc se da al reemplazar las expresiones de
presión y velocidad de partícula de una onda plana en la ecuación de impedancia
acústica específica [7].
[
donde
es la densidad del aire y
]
(9)
es la velocidad del sonido.
5.1.1.3 Reacción local y extendida
Generalmente, la velocidad normal en un punto
sobre una superficie depende
de la presión en todos los puntos . La reacción extendida se refiere a que las
ondas pueden viajar libremente a lo largo de una superficie, y la impedancia no
puede ser definida de forma única. Si se tiene una onda plana incidente, se podría
definir un valor de impedancia para cada ángulo de incidencia 𝜙 [8].
Sin embargo, en los casos de material absorbente, el movimiento de la onda
dentro del medio es fuertemente atenuado por la disipación viscosa, esto se
conoce como reacción local, así que la velocidad normal en un punto x depende
sólo de la presión en ese punto [8].
Para un sistema con reacción local, la relación entre la presión y la velocidad
normal es independiente de la forma del campo incidente. Entonces la impedancia
es efectivamente independiente del ángulo 𝜙 [8].
5.1.2 Propagación de ondas sonoras en un tubo
La propagación de las ondas sonoras dentro de un tubo toma forma de ondas
estacionarias con desplazamiento en dirección al eje . Dichas ondas se generan
a partir de las interferencias constructivas y destructivas producidas por la
15
superposición de la onda incidente y reflejada en el extremo rígido dentro del tubo,
formando así máximos y mínimos de presión que
varían de acuerdo con la
frecuencia de la onda que se está propagando. Dicho fenómeno se conoce como
modo de vibración. Para el caso de caracterización del coeficiente de absorción
por medio del tubo de impedancias, es necesario saber que la velocidad y presión
toman su valor mínimo respectivamente cuando [9]
|
(10)
|
(11)
donde,
n= 0, 1, 2, 3….
= Longitud de onda (m)
5.1.3 Materiales acústicos absorbentes de sonido
Para el desarrollo de este proyecto, sólo se caracterizarán materiales de tipo
poroso y fibroso, que dentro de los materiales absorbentes, son los que poseen
mejores propiedades para la absorción del sonido.
5.1.3.1 Absorción en materiales porosos
La propagación del sonido ocurre en una red de poros interconectados, y debido a
los efectos viscosos y térmicos del material, es causada la disipación de la energía
sonora [10]. Cuando el sonido se propaga por espacios pequeños como los poros
de un material poroso absorbente, la energía se pierde, esto es debido a los
efectos de la capa límite viscosa.
El aire es un fluido viscoso,
y
consecuentemente, el sonido es disipado por la fricción con las paredes de poros,
también hay una pérdida debido a los cambios en el flujo cuando el sonido se
mueve a través de los poros irregulares [10].
Así como las pérdidas viscosas, también habrá pérdidas debido a las condiciones
16
térmicas del aire al material absorbente; esto es más significativo a altas
frecuencias. Para que la absorción sea efectiva, debe existir canales
interconectados a través del material, por lo que es necesaria una estructura con
poros abiertos [10]. La absorción también depende del grosor del material,
generalmente es directamente proporcional a la absorción en bajas frecuencias
[10].
5.1.3.1.a Absorción de una superficie plana de impedancia uniforme
Con base en un modelo localmente reactivo, es posible calcular el coeficiente de
absorción en términos de la resistencia, la reactancia y el ángulo de incidencia de
una onda sobre una superficie infinita y con impedancia uniforme. De acuerdo con
la Figura 2, las presiones incidente y reflejada pueden ser expresadas como [8]:
Figura 2 Incidencia de una onda plana sobre una superficie infinita con impedancia uniforme [8]
(12)
(13)
donde
𝜙y
𝜙.
En la superficie del plano, x=0.
(14)
y la componente normal de la velocidad de partícula es
17
(15)
𝜙
Sabiendo que
𝜙, entonces
𝜙
(16)
y
(17)
𝜙
Organizando la proporción de amplitudes de la onda incidente y reflejada
𝜙
𝜙
donde
que
es
la
(18)
impedancia
acústica
específica
normal
adimensionada.
Las potencias Incidente y reflejadas están definidas como:
| |
𝜙
| |
(19)
(20)
𝜙
El coeficiente de absorción está definido como la proporción de la energía que
incide con respecto a la que se refleja, por lo que el coeficiente de absorción de
potencia acústica es [8]:
𝜙
| |
|
𝜙
𝜙
|
(21)
5.1.3.1.b Modelos para materiales absorbentes de sonido.
En general, el comportamiento acústico de los materiales porosos, considerados
como isótropos y homogéneos, queda definido por la impedancia característica y
por la constante de propagación, que pueden calcularse en función de la
resistencia al flujo del material, que se designa con la letra
[7]. Muchos autores
han diseñado modelos con el fin de describir el comportamiento de dichos
18
materiales, entre los más conocidos se encuentran Delany y Bazley, y
posteriormente Miki con sus modificaciones al modelo de los autores anteriores
[7]. La mayoría de los modelos son para materiales con alta porosidad, y permiten
obtener la impedancia característica y la constante de propagación a partir de las
propiedades físicas de los materiales [7]. En este trabajo investigativo se hará uso
del modelo de Allard y Champoux para la descripción de los materiales medidos a
partir el valor de resistencia al flujo obtenido.
5.1.3.1.b.1 Modelo de Allard y Champoux
Los autores desarrollaron un modelo a partir de una muestra de materiales de tipo
fibroso que sustituye al modelo de Delany y Bazley. Dicho modelo propone una
corrección a bajas frecuencias y establece la dependencia de otras propiedades
físicas como el diámetro de las fibras y la densidad, involucrando por primera vez
la geometría del material en un modelo matemático [7].
Las ecuaciones de impedancia característica y constante de propagación están
dadas por:
√
(22)
(23)
√
[kg/m3] Es la densidad dinámica.
[N/m2] Es el módulo de compresibilidad efectivo dinámico.
Dichas cantidades se pueden expresar con una temperatura ambiente y presión
atmosférica por las siguientes ecuaciones:
√
(
)
19
(
)
(24)
(25)
Con
en Hz y
√
(
)
(
)
√
(
)
(
)
en Rayls/m.
Las ecuaciones anteriores son válidas únicamente para incidencia normal y
asumiendo que los materiales disponen de valores de porosidad y tortuosidad
altos y cercanos a la unidad [7].
La constante de propagación
normal
y la impedancia característica a incidencia
están dadas por las ecuaciones (26) y (27).
[
]
[
(26)
]
Se define la impedancia superficial
(27)
para una capa de espesor con terminación
rígida.
(28)
Y el coeficiente de absorción
|
|
(29)
5.1.3.2 Características físicas de los materiales absorbentes
Los materiales absorbentes del sonido de tipo poroso se clasifican en absorbentes
de esqueleto rígido y absorbentes de esqueleto flexible .En los absorbentes
sonoros de esqueleto rígido el coeficiente de absorción aumenta con la frecuencia.
Por su parte, en los absorbentes sonoros de esqueleto flexible se producen
resonancias a frecuencias bajas y medias [7]. Dichos materiales cuentan con
ciertas características físicas que influyen en el comportamiento del mismo a la
hora de absorber sonido.
20
5.1.3.2.a Isotropía y homogeneidad
La homogeneidad infiere que las características del material son las mismas en
todos los puntos de la muestra. La cualidad de isotropía supone que las
características son iguales en un punto de la muestra independiente de la
dirección en que se evalúe [7].
5.1.3.2.b Porosidad
La porosidad está definida como la relación del volumen de agujeros de aire y el
volumen total del material, es una cantidad adimensional que es menor a la unidad
[8]. Los métodos de medición de esta cantidad involucra el uso de sustancias
líquidas para determinar el volumen de aire que no es ocupado por el material, sin
embargo, se han desarrollado métodos acústicos alternativos usando impulsos de
ultra sonido reflejados en la primera interfaz de un bloque de material poroso
saturado de aire, este método ha sido exitoso en espumas de plástico y
aglomerados de granos [11].
5.1.3.2.c Tortuosidad
Es el grado de irregularidad y variación de la dirección del canal, se puede evaluar
con ultrasonido [8]. A altas frecuencias es responsable de la diferencia entre la
velocidad del sonido en el aire y la velocidad del sonido a través del material. La
tortuosidad en un material fibroso común usado en control de ruido es un poco
mayor que 1, mientras que la porosidad es cercana (pero nunca mayor) que 1. En
un material rígido poroso, la tortuosidad es una de las propiedades que contribuye
al “factor de estructura” que está relacionado con la “masa adicionada” usada en la
teoría de la propagación del sonido en materiales porosos y elásticos [11].
5.1.3.2.d Resistencia al flujo de aire y resistividad al flujo.
El parámetro más importante para determinar el comportamiento acústico en
materiales porosos delgados, es la resistencia al flujo de aire. Representa la razón
del gradiente de presión aplicado y el flujo de volumen inducido, tiene unidades de
presión dividida por la velocidad [11], también está definida como la relación entre
21
la caída de presión y la velocidad del flujo a través de una muestra de material.
Los autores Ingard y Dear obtienen el valor de resistencia al flujo a partir de la
impedancia al flujo normalizada, siendo la parte real la resistencia y la parte
imaginaria la reactancia al flujo [7]. La resistividad al flujo, se define como la
medida de la resistencia al flujo por unidad de espesor, también es llamada como
resistencia específica al flujo por unidad de espesor [11], depende principalmente,
de la densidad del material y del tamaño de la fibra [7].
Si un material tiene alta resistividad al flujo, significa que es difícil que el aire fluya
a través de la superficie, la resistividad al flujo es proporcional al espesor [10] e
inversa a la permeabilidad, baja permeabilidad resulta de baja porosidad en la
superficie [11]. En materiales fibrosos, la resistencia al flujo depende de la
densidad aparente y del diámetro de la fibra, una disminución en el diámetro de la
fibra, es un aumento en la resistividad al flujo y en la absorción del sonido,
materiales efectivos son aquellos que poseen fibras muy finas [10].
La resistencia específica al flujo está medida como
[
]
(30)
Y la resistividad al flujo o resistencia específica al flujo por unidad de espesor se
obtiene cuando
[
dónde
]
(31)
es el diferencial de la presión estática a través de una capa homogénea
de espesor
,
es la velocidad de un flujo estable a través del material, V es el
volumen de aire pasando a través de la muestra durante un periodo de tiempo T y
S es el área de la cara de la muestra [11]. En general la dependencia de la
resistencia al flujo con la velocidad de partícula se vuelve importante cuando se
considera el comportamiento de los materiales porosos en altos niveles de presión
sonora [11].
22
Para casi todos los materiales granulados o fibrosos absorbentes de sonido, el
valor de la resistencia al flujo no puede predecirse analíticamente a partir de la
geometría del esqueleto, esta cantidad debe ser medida. Para algunos materiales
absorbentes ideales, como los hechos de esferas idénticas o fibras paralelas e
idénticas, es posible hacer una predicción [11].
A menudo la resistencia específica al flujo es caracterizada por medio de métodos
que no son acústicos, usando la expresión de Bies y Hansen [12].
(32)
dónde,
= Densidad del material
d = Diámetro medio de las fibras
Este método de caracterización, no es válido para materiales de tipo granular, a
los cuales no se les puede determinar el diámetro de la fibra [13]. Sin embargo,
existen protocolos acústicos de medición para caracterizar dicha cantidad como el
propuesto por los autores Ingard y Dear, el cual se profundizará posteriormente en
este trabajo.
5.1.3.2.d.1 Aplicaciones del valor de resistencia al flujo en soluciones
acústicas
- Absortores de sonido usando capas delgadas
Capas rígidas
Se le llama absortores de sonido a aquellas construcciones que han sido
diseñadas con el propósito de tener un alto rendimiento en la absorción de sonido
en una banda de frecuencia, ya sea estrecha o amplia. Existen ciertas
23
configuraciones de absortores que pueden describirse a partir de unos pocos
parámetros medibles [11].
Figura 3 Capa delgada de material absorbente al frente de un espacio de aire respaldado por una pared
rígida. A. Espacio de aire localmente reactivo (Pariticionado). B. Espacio de aire no particionado.
Una capa delgada resistiva al flujo en frente de una pared rígida con un espacio de
aire (Figura 3), puede ser completamente caracterizada por su resistencia al flujo o
por su impedancia normalizada
velocidad del fluido. [11].
particionado es
donde
es la densidad y
la
La impedancia normalizada de un espacio de aire
donde
es el número de onda,
es la
longitud de onda y t es la profundidad del espacio de aire.
La impedancia de aire normalizada del muro para incidencia normal
es
(33)
La impedancia del aire es cero cuando
que ocurre para frecuencias
donde la profundidad del espacio de aire es un múltiplo entero de un cuarto de
longitud de onda. El valor máximo del coeficiente de absorción para incidencia
normal es.
24
(34)
Ingard simuló la absorción de sonido de una capa resistiva al flujo rígida en frente
de un espacio de aire particionado (Reacción local) y un espacio de aire no
particionado (Reacción no local) respaldados por una pared rígida para incidencia
normal e incidencia aleatoria (Figura 4).
La figura muestra que para un espacio con reacción local, la absorción máxima
para incidencia normal se presenta para frecuencias donde la profundidad del
espacio del aire corresponde a un múltiplo entero de cuartos de longitud de onda
con
Esto ocurre porque la presión en el espacio de aire es
cero debido a que el sonido reflejado en la pared tiene un desfase de 180 grados,
esto genera que el gradiente de presión a través de la capa de material poroso
alcance su máximo valor, el cual es numéricamente igual a la presión en el lado
incidente del material
donde
es la amplitud de la presión que
incide y R es el factor de reflexión [11].
(35)
Este gradiente de presión produce una velocidad de partícula
a través
de la capa del material, y la potencia sonora disipada por unidad de superficie del
absortor
(36)
Para
,
, y
, indica que toda la energía sonora
incidente es disipada en la capa porosa. Para valores de
máximo pero sin llegar a 1. Mientras
difiera más de
absorción será más pequeño [11].
25
es aún un
el coeficiente de
Figura 4 Coeficiente de absorción de una capa delgada rígida resistiva al flujo respaldada por un muro
rígido en función de la frecuencia normalizada en forma de la razón del grosor del espacio de aire y la
longitud de onda, contra la resistencia al flujo normalizada. A. Incidencia normal. B. Incidencia
aleatoria para un espacio de aire con reacción localizada. C. Incidencia aleatoria para un espacio de
aire con reacción no localizada [11].
Para incidencia aleatoria, los valores máximos del coeficiente de absorción se
presentan en las mismas frecuencias que para incidencia normal, sin embargo no
existe un valor de resistencia al flujo para una máxima absorción [11].
Capas flexibles
Es de saber que el uso de capas flexibles y resistivas, pueden proporcionar una
alta absorción a frecuencias más bajas que con el uso de capas rígidas, sin
embargo se debe ser precavido al diseñar absortores para aplicaciones donde se
26
requieren altos niveles de presión sonora. La capa flexible debe ser capaz de
soportar las tensiones debidas a las grandes amplitudes del movimiento de la
onda incidente sin fatiga alguna [11]. Cuando se usan capas flexibles, la masa por
unidad de área de la capa y la rigidez por unidad de área del espacio de aire entre
la capa y la pared rígida, resultan en un sistema resonante, cerca de la frecuencia
de resonancia se presenta el máximo movimiento. Aproximadamente, la
frecuencia de resonancia está dada por
(
dónde
(37)
)
es el coeficiente de compresión adiabática, t es el grosor del
espacio de aire en metros, y m’’ es la masa por unidad de área del material flexible
en kilogramos por metro cuadrado. El coeficiente de absorción para este tipo de
absortores también fue simulado, la Figura 5 muestra dicho coeficiente para
incidencia normal en función de la frecuencia normalizada
resistencia al flujo normalizada de un material poroso
, con la
como parámetro
para varias relaciones de la masa del material y la masa de aire del espacio,
[11].
La figura expone que el primer valor máximo de coeficiente de absorción a
incidencia normal se presenta cerca de la frecuencia de resonancia. Mientras más
grande sea la relación de masa MR, a más baja frecuencia se presenta el pico de
máxima absorción. También es de notar que el pico del coeficiente de absorción
es la unidad cuando la relación de masa MR es igual a la resistencia al flujo
normalizada. Para obtener una absorción relativamente alta a bajas frecuencias en
una amplio rango, un valor de resistencia al flujo normalizado entre 2 y 3 parece
ser una buena opción.
27
Figura 5 Coeficiente de absorción a incidencia normal de una capa flexible y resistiva en frente de un
espacio de aire [11].
- Ductos recubiertos
Usualmente se hace uso de silenciadores disipativos para atenuar los ventiladores
en sistemas de aire acondicionado. La disipación de la energía sonora
generalmente se logra aplicando recubrimientos de materiales porosos en una o
más paredes dentro del ducto por donde viaja la onda, en ciertos casos, el
28
material poroso debe tener una cubierta protectora [10]. Cuando las dimensiones
del ducto recubierto son muy grandes comparados con la longitud de onda del
sonido propagado, se presentan modos de orden superior dentro del ducto [10].
Cuando se analiza la propagación del sonido dentro de un ducto recubierto de
material absorbente, se usa una de las dos suposiciones más comunes. La más
antigua, común y por lo tanto más investigada, es que el recubrimiento debe ser
tratado como localmente reactivo, en este caso, el recubrimiento es tratado con
impedancia local, que es independiente de lo que suceda en cualquier otro lado
del mismo y está implícito que la incidencia del sonido no es otra que normal a la
superficie [10]. Cuando la propagación del sonido en el recubrimiento es paralela
la superficie,
el análisis requiere una nueva suposición donde se dice que el
recubrimiento tiene reacción extendida, en este caso, la propagación en el
recubrimiento se tiene en cuenta [10].
Generalmente, los recubrimientos en los ductos son hechos de material poroso
absorbente, por lo que deben estar caracterizados con valores de impedancia
específica y resistividad al flujo. Para materiales homogéneos ambas cantidades
están relacionadas entre sí junto con el espesor. La resistividad al flujo de un
material poroso uniforme es una función de la densidad del material,
consecuentemente, un recubrimiento de este tipo de materiales debe disponer del
valor de la densidad específica [10].
Diseño de silenciadores para ductos recubiertos
Se presentan a continuación algunos diseños de silenciadores para ductos a partir
de módulos de predicción simplificados, vale aclarar que dichos diseños presentan
algunas limitaciones. Se consideran recubrimientos con reacción local y extendida,
donde se determina la tasa de atenuación del modo menos atenuado para algunos
casos, no son óptimos, pero no son muy sensibles a la precisión del valor de la
resistencia
al
flujo
del
recubrimiento,
dichos
diseños
son
simulados
computacionalmente variando ciertos parámetros con el fin de observar su
29
influencia en la tasa de absorción, sin embargo existen procedimientos disponibles
para lograr una óptima atenuación sonora, pero generalmente mientras más alta la
atenuación, más susceptible es la especificación de la resistencia al flujo y el
rango de frecuencias donde es efectivo el recubrimiento es más cerrado.
Figura 6 Atenuación en un ducto rectangular recubierto en los lados opuestos. Reacción Local [10].
En la Figura 6 se muestra la atenuación de un recubrimiento con reacción local
para varios valores de resistividad al flujo
y la relación del grosor del
recubrimiento con la mitad de la altura del ducto
, para una longitud de ducto
igual a la mitad de su ancho. En esta figura, la densidad es cero. Se asume que la
resistencia al flujo del recubrimiento es la misma en dirección normal al eje del
ducto como lo es en dirección paralela [10].
30
- Absortores Resonantes
Micro-perforaciones
Si un material micro-perforado es usado sin respaldo rígido, puede ser usado
como un absortor suspendido, atenuando el sonido incidente por ambos lados.
Figura 7 Coeficiente de absorción para diferentes dispositivos micro-perforados [14].
La Figura 7 compara la atenuación generada por dos materiales micro-perforados
con respaldo rígido contra la generada por una capa doble micro-perforada sin
respaldo y suspendida en el aire, la absorción es dada solamente por la disipación
en el dispositivo, el sonido transmitido no es considerado [14]. La doble capa
suspendida en el aire provee absorción en frecuencias bajas únicamente debido a
la resistencia al flujo, y es máxima cuando la resistencia al flujo de la estructura es
, la absorción adicional a bajas frecuencias, es debido a la atenuación en
frecuencias medias [14].
31
- Otros absortores
Mecanismo de Flujo de Energía
Considere una onda sonora incidiendo en un difusor de Schroeder. Por
simplicidad, considere solo 2 agujeros adyacentes, además considere que uno de
los hoyos se encuentra en resonancia con el sonido que está incidiendo mientras
el otro hoyo no. Como se muestra en la Figura 8, la energía en la boca del agujero
resonante, será mucho mayor que en el agujero que no resuena, esto significa que
habrá un flujo de energía
del agujero resonante al agujero no resonante,
consecuentemente, cerca a las entradas de los hoyos hay alta velocidad de
partícula, 14 veces mayor que la presente en la onda incidente. Como el sonido se
mueve cerca de los bordes, de un hoyo al otro, se presenta máxima absorción
[14].
s
Figura 8 Dos agujeros adyacentes de un difusor de Schroeder [14].
Sabiendo que la cara frontal del difusor es una región de alta velocidad de
partícula, tiene sentido ubicar material absorbente en la entrada de los hoyos si se
desea crear un absortor, esto convierte a los difusores en unos potentes
absorbentes. La Figura 9 muestra el coeficiente de absorción de una superficie
perfilada con y sin cubierta resistiva. Se exponen dos capas con diferentes valores
de resistencia al flujo, el efecto de la capa resistiva es ampliar los picos
resonantes, generando absorción en un ancho de banda mucho mayor [14].
También se incrementa la impedancia cerca a la impedancia característica del aire
por lo que se genera más absorción.
32
Figura 9 Variación del coeficiente de absorción a incidencia normal de un difusor según la cubierta
[14].
La resistencia de la cobertura debe ser tal que la resistencia total de los hoyos
esté cerca de la impedancia característica. Resistencia muy grande tiende a sobre
amortiguar el sistema y los picos de absorción estarían muy disminuidos. Poca
resistencia (Sin cubierta) genera un comportamiento dispar, mucha resistencia
(550 Rayls )tiene a sobre amortiguar, mientras que 65 Rayls proporciona los picos
máximos de absorción [14].
5.1.4 Métodos de medición para la caracterización de materiales acústicos
Existen diferentes métodos de medición para la caracterización de materiales
acústicos, sin embargo, uno de los métodos más aplicados durante el desarrollo
investigativo de los materiales para la acústica, es el tubo de Kundt o también
conocido como el tubo de impedancias, a continuación se presentan los
conocimientos más relevantes acerca dicho método para el desarrollo de esta
investigación.
33
5.1.4.1 Tubo de Kundt o tubo de impedancia
El tubo de impedancia (Figura 10) es un método muy útil ya que permite hacer las
mediciones en condiciones muy definidas y controladas sin requerir de muestras
muy grandes ni recintos especializados. Este método es utilizado especialmente
para medir materiales absorbentes de tipo poroso, ya que para otro tipo
de
materiales absorbentes, las muestras pequeñas no son representativas para el
comportamiento de la absorción en las muestras grandes.
El funcionamiento del tubo se basa en la teoría de ondas estacionarias, reflexión,
superposición e interferencia de las ondas [9].
Figura 10. Tubo de impedancia. Arriba: Montaje con sonda. Abajo: Montaje con dos micrófonos [15].
El campo de sonido dentro del tubo puede ser considerado como una suma de las
ondas planas y los modos superiores. El sonido es guiado internamente y forzado
a propagarse en la dirección axial del tubo [15].
A continuación se presenta un acercamiento al origen del método de medición y
las aplicaciones e investigaciones que se desarrollan en la actualidad, las cuales
están directamente ligadas con el desarrollo y caracterización de nuevos
materiales acústicos a partir de materiales alternativos.
34
La creación del tubo de Kundt como método de medición para la caracterización
de materiales acústicos se debe al físico alemán August Adolf Eduard Eberhard
Kundt (1839 – 1894) quién fue el sucesor de H. von Helmholtz y director del Berlin
Physical Institute. El físico se enfatizaba a estudiar acerca de las áreas de la luz y
el sonido, y es cuando desarrolló un método de medición de las ondas dentro de
tubos situando un material en forma de polvo y haciéndolo vibrar, de tal manera
que podía observar los diferentes modos de vibración que se presentaban al
interior del montaje [7].
A partir de dicho desarrollo, varios investigadores realizaron variantes al tubo para
ejecutar diferentes tipos de medición, y es cuando en el año 1945, Scott describió
un método para medir la constante de propagación directamente y luego obtener
la impedancia característica de un material poroso [7].
Por medio de modificaciones a través del tiempo es como se llegó a los modelos
hoy utilizados para la caracterización de materiales absorbentes.
Método tasa de ondas estacionarias.
Técnica de dos micrófonos.
Actualmente se cuenta con estándares internacionales de medición con el tubo de
impedancias, estos estándares son:
5.1.4.1.a ISO 10534-1 / ASTM C384 “Acústica – Determinación del coeficiente
de absorción e impedancia en tubos de impedancia. Parte 1: Método de la
tasa de ondas estacionarias”
El proceso que recomienda la norma consiste en ubicar una muestra del material
absorbente al final del tubo, por medio de un altavoz se genera un tono puro con
cierta frecuencia que se propaga en forma de onda plana hasta llegar al material,
causando que éste absorba y/o refleje el sonido de acuerdo con sus propiedades
físicas, creando una interferencia entre la onda incidente y la reflejada. Las
interferencias crean ondas estacionarias dentro del tubo, y mediante rastreo con el
35
micrófono, se ubican los valores máximos y mínimos de nivel de presión y sus
distancias.
Como primer paso para calcular el coeficiente de absorción para incidencia
normal, se calcula la razón de la onda estacionaria S1 con las presiones del primer
mínimo y del primer máximo [16].
|
|
|
|
(38)
Con dicho valor y la distancia del mínimo, se calcula el factor de reflexión
| |
donde
(
)
(39)
es la corrección de la atenuación por viscosidad,
del primer mínimo,
es la razón de onda estacionaria y
es la distancia
es la longitud de onda.
Y finalmente se obtiene el valor del coeficiente de absorción
| |
(40)
5.1.4.1.b ISO 10534-2 / ASTM E1050-12 “Acústica – Determinación del
coeficiente de absorción e impedancia en tubos de impedancia. Parte 2:
Método de función de transferencia”
Este método es similar al anterior, se dispone de un tubo y de una muestra al final
en el extremo rígido del mismo, en el extremo contrario se ubica el altavoz que es
la fuente sonora generadora de ondas planas las cuales se propagan hasta llegar
a la muestra, esto permite medir la presión en dos puntos del tubo cercanos al
material, donde se encuentran ubicados dos micrófonos. Se calculan los valores
36
del factor de reflexión complejo, el coeficiente de absorción y la relación de
impedancia del material a incidencia normal a partir de la función de transferencia
compleja de las señales de los dos micrófonos. El ancho de banda en el que
trabaja el tubo se determina por el ancho del mismo y la distancia entre las
posiciones de medida de la presión [17].
5.1.4.2 Método de Ingard y Dear para la medición de la resistencia específica
al flujo de aire
Como es posible notar, estos estándares se realizan sólo para medir el coeficiente
de absorción, el coeficiente de reflexión compleja y la impedancia acústica del
material, también existen otras cantidades que sirven para caracterizar
acústicamente un material, una de esas cantidades es la resistencia al flujo de
aire, siendo esta motivo de esta investigación. Durante el desarrollo del tubo de
Kundt, se realizaron investigaciones que utilizan el mismo montaje experimental
para la medición de dicha cantidad, descubriendo así una nueva aplicación para el
tubo y las ondas estacionarias.
Este método se basa en la medición con el tubo de impedancia, haciendo uso de
dos micrófonos ubicados en dos posiciones diferentes dentro del tubo, el primero
antes de la muestra del material y el segundo en el extremo contrario a la fuente
sonora justo en la terminación rígida (Figura 11).
Figura 11. Montaje Ingard & Dear [18].
La resistencia al flujo está definida como una relación entre la caída de presión y
la velocidad de volumen través de la muestra [19], se mide con dos micrófonos
37
ubicados en el tubo como se muestra en la Figura 11.
Supuestos del método de medición:
La caída de presión es suficientemente pequeña para que la velocidad se
considere igual en ambas caras de la muestra.
El espesor de la muestra es mucho menor de la longitud de onda, por lo
que la velocidad se considera constante a través del material.
Condiciones del método de medición:
La longitud de onda debe ser mayor que 1.7 veces el diámetro del tubo.
(41)
La longitud L debe ser múltiplo impar del cuarto de longitud de onda de la
frecuencia a medir.
(42)
Con la distancia entre la muestra y la terminación rígida denotada por L, es posible
expresar la relación entre la velocidad U1 en la muestra y la presión P2 en la
terminación rígida [19].
(43)
Siendo K el número de onda. Similarmente, la amplitud compleja de la presión en
la parte posterior de la muestra (P1’) es
(44)
La impedancia al flujo está definida como
(45)
Reemplazando las ecuaciones (43) y (44)
(46)
De acuerdo con los autores, si se escoge L=(2n-1)λ/4 para valores de n= 1,2,…la
impedancia al flujo normalizada se da
38
(47)
Siendo la resistencia al flujo la parte real y la reactancia la parte imaginaria [19],
por lo que
|
( )|
(48)
Definiendo la función de transferencia como
(49)
Entonces la resistencia al flujo se puede determinar como la impedancia
normalizada
|
(
)|
(50)
A bajas frecuencias la reactancia al flujo es pequeña en comparación con la
resistencia al flujo, por lo que se puede hacer la siguiente simplificación [19].
| |
|
|
(51)
La expresión también puede presentarse en términos de nivel de presión sonora
( )
(52)
Así que midiendo los valores de nivel de presión sonora en los puntos P1 y P2
(ubicación de micrófonos en el montaje, ver Figura 11) de las diferentes
frecuencias, el valor de la resistencia al flujo normalizada puede representarse por
la siguiente expresión
(
)
(53)
5.2. ESTADO DEL ARTE
Los primeros en obtener mediciones de la resistencia al flujo son Delany y Bazley,
pues utilizaron dicha cantidad para expresar los resultados de las medidas de
impedancia característica y la constante de propagación. En su trabajo, las
relaciones empíricas requieren sólo el conocimiento de la resistencia al flujo del
39
material, la cual fue obtenida directamente de medir la presión sonora a través la
muestra con una velocidad volumétrica de flujo conocida pasando a través de la
misma [7].
En el año 1979, los autores Bies y Hansen desarrollaron un trabajo en el que se
usó el parámetro de la resistencia al flujo para caracterizar completamente el
comportamiento acústico de un material poroso, demostraron que a partir de la
medición de la resistividad al flujo se puede describir la propagación del sonido
[7].
Luego en 1992 Ren y Jacobsen midieron la resistencia y la reactancia al flujo de
los materiales porosos. Utilizando un método de medición basado en el tubo de
impedancia acústica, midiendo la función de transferencia entre dos micrófonos
que se sitúan antes y después de la muestra [7]. El trabajo de estos autores es de
gran importancia en el desarrollo investigativo de la medición de dicha cantidad
debido a los avances expuestos en sus investigaciones.
Para las medidas de resistencia al flujo de aire también existen estándares
internacionales, como la UNE EN ISO 29053:1994 la cual propone dos métodos
de medición, el método con flujo de aire directo (A) y el método con flujo de aire
alterno (B) , el primero consiste en pasar un flujo de aire de una sola dirección y
controlado a través de una probeta y medir la pérdida de presión resultante entre
las dos caras libres de la probeta; el segundo consiste en pasar un flujo de aire
lento a través de la probeta y medir la componente alterna de la presión en el
volumen de ensayo ocupado por la probeta. Ambos métodos requieren de
montajes especializados [20].
El método más actual para la medida de la resistencia al flujo, lo desarrollaron los
autores R. Dragonetti, C. Ianniello y R. A. Romano como una alternativa diferente
40
a la norma mencionada, este requiere de dos cavidades de sección cuadrada, la
muestra se ubica en la parte posterior de la cavidad superior sobre una rejilla con
perforaciones y el altavoz se ubica en medio de las dos cavidades (la inferior tiene
dimensiones muy pequeñas comparadas con las dimensiones del altavoz), son
necesarios dos micrófonos de medición que son ubicados por separado en las
cavidades. Este método cumple con los requerimientos necesarios de la norma
UNE EN ISO 29053:1994, pero con materiales que son más asequibles [20].
Actualmente los estudios acerca la resistencia al flujo de aire se basan en la
comparación e incertidumbres de los métodos de medición mencionados y en
proponer modificaciones para el mejoramiento de las medidas. Este estado de
conocimiento se enfoca en el desarrollo investigativo en la obtención de la variable
mencionada, tomando como eje central el método de Ingard y Dear el cual es
objetivo de esta investigación.
España se ha especializado en dicho tema y todo lo que tiene que ver con
caracterización de materiales. En el 2006 se desarrolló un estudio de la
incertidumbre en el método de medición de resistencia al flujo de Ingard & Dear,
comprobando la precisión de la simplificación que los autores proponen para las
diferentes frecuencias [18], se construyó el tubo para el montaje y a partir de esto
se ha profundizado más en el tema realizando comparaciones entre métodos de
medición. En el 2013 se evaluó el método de Ingar y Dear contra el método de R.
Dragonetti y C. Ianniello y el de la norma UNE EN ISO 29053:1994 (B), para esto
se usaron diferentes tipos de materiales; para algunos de ellos, los métodos
alternativos arrojaban resultados similares entre sí, pero diferentes con respecto a
el método estandarizado; para otros sucedía lo contrario [21], sin embargo se llegó
a la conclusión de que estos métodos alternativos son una muy buena opción y no
requieren de materiales ni recintos especiales.
41
También existen avances en métodos que no son acústicos, como el desarrollado
por la ISO 29053:1994, dichos métodos no son de interés en el proyecto debido a
la desviación en el tema de investigación.
Con respecto a la elaboración de materiales acústicos a partir de materia prima
alternativa, se han desarrollado diferentes investigaciones y pruebas, todas con el
fin de desarrollar materiales acústicos eficientes y que no sean nocivos para la
salud humana. En el 2005 en Italia se desarrolló un modelo empírico de un
material acústico a base de fibras de polyester, esta investigación propone nuevos
modelos matemáticos para la resistencia al flujo y para la impedancia acústica
[22]. España también se ha especializado en este tema, el cual va muy ligado a
las investigaciones de los métodos de medición para la caracterización de los
materiales acústicos. En la Universidad de Alicante y la Universidad Pontificia de
Valencia
disponen
de
los
laboratorios
necesarios
para
este
tipo
de
investigaciones. En el 2008 se publicó una tesis doctoral muy completa que habla
de los diferentes métodos de medición para la caracterización de los materiales
acústicos [7], dicha tesis profundiza en cada método mencionado para la
absorción y resistencia al flujo; caracterizan varios tipos de materiales incluyendo
sándwiches de fibras textiles, combinaciones con materiales conocidos como la
fibra de vidrio y lana de roca, entre otros; y proponen nuevos modelos
matemáticos basados en los métodos de medición para la caracterización de
materiales. Posteriormente en el 2010 se realizó una investigación para el
desarrollo de un nuevo material basado en fibras de Kenaf y se propusieron
ecuaciones empíricas que modelan el comportamiento acústico del material en
términos de absorción y resistencia al flujo [23], dicho modelo se basa en modelos
anteriormente propuestos por otros autores.
Un año después (2011) los mismos autores desarrollaron el mismo trabajo
investigativo para un material acústico a base de restos de botellas de plástico,
42
usando el mismo proceso industrial que se utiliza para las fibras de polyéster,
también desarrollaron un modelo del comportamiento acústico para este material
[24].
El trabajo investigativo más reciente de los mismos autores es basado en el
desarrollo de un nuevo material a partir de fibras de coco (2014), caracterizando
dicho material y realizando un modelo matemático para su comportamiento
acústico, como lo hicieron con los materiales desarrollados en años anteriores
[25].
En el 2006 en Colombia se desarrolló una investigación de materiales acústicos
desarrollados a partir de desechos de poliéster de la industria textil y fibras
vegetales como la fibra de coco, este estudio se realizó en la Universidad de San
Buenaventura Bogotá por dos estudiantes del programa de Ingeniería de Sonido.
Este trabajo es investigativo-experimental ya que por medio de pruebas de
aglomeración de la materia prima previamente escogida en diferentes moldes y
con diferentes aglomerantes, se elaboró un panel para uso en acústica
arquitectónica y control de ruido, dicho panel sólo es caracterizado con valores de
coeficiente de absorción para diferentes frecuencias obtenidos del promedio de 18
mediciones por medio de tubo de resonancia Pasco WA-9612, los resultados de
estas mediciones arrojaron valores de coeficiente de absorción entre 0,7 y 0,9,
teniendo el valor máximo en la frecuencia de 500 Hz [26].
En este trabajo investigativo se pretende entonces analizar una posible aplicación
acústica de un material alternativo que tiene fines diferentes en la ciudad, además
de caracterizarlo con valores de coeficiente de absorción y resistencia al flujo de
aire obtenidos de las mediciones con el tubo de onda estacionaria y por el método
de Ingard & Dear respectivamente, ambos métodos se explican con detalle en el
marco conceptual de este proyecto. Se requiere entonces una comparación de los
43
valores obtenidos del material alternativo contra los valores de los materiales
acústicos tradicionales para evaluar las posibilidades de aplicación.
6. METODOLOGÍA
A continuación se presenta el proceso llevado a cabo en la búsqueda del
cumplimiento de los objetivos planteados; este proceso está basado en las
actividades planeadas para cada objetivo, consta de diferentes fases: Selección
de los materiales a caracterizar, medición del coeficiente de absorción de los
materiales, diseño y construcción del tubo para la medición de resistencia al flujo,
desarrollo de dicha medición, análisis de los resultados, evaluación de la
aplicación alternativa y conclusiones; cada fase explicará con detalle en secciones
posteriores.
Selección de los materiales a caracterizar.
Medición del coeficiente de absorción.
Diseño y construcción del tubo para resistencia al flujo.
Medición de resistencia al flujo.
Análisis de resultados
Evaluación de aplicación alternativa.
Conclusiones
Figura 12 Diagrama de flujo de la metodología.
6.1 Materiales utilizados para la caracterización
Como primer paso se requería la selección de los materiales a caracterizar, ésta
se dividió en 2 partes, la primera consistió en definir los materiales acústicos
tradicionales para la comparación, y la segunda, en la elección del material
44
alternativo a evaluar.
Se eligieron materiales acústicos desarrollados en la industria Colombiana a base
de lana mineral de roca y fibra de vidrio, los cuales fueron proporcionados por los
fabricantes con fines investigativos. Se calculó un valor de densidad aproximado
de las muestras de cada material a partir del volumen y la masa, ya que no todos
los fabricantes proporcionaban dicha información.
Acustiplaca
Figura 13 Acustiplaca [27]
Láminas de alta densidad (Figura 13), presentan gran rigidez por lo que conservan
su forma constantemente; desarrolladas de lana mineral de roca por la empresa
Calorcol. Dispone de características de incombustibilidad, es usada para
recubrimientos acústicos de paredes y techos, y como núcleo de aislamiento
acústico y control de ruido [27], en la Tabla 1 se exponen las especificaciones
brindadas por los fabricantes.
45
Tabla 1 Acustiplaca, Especificaciones técnicas del fabricante [27].
80, 100 y 144 kg/m3.
Densidad Fabricante
Coeficiente de reducción de ruido (NRC)
NRC 0.90 en 2 plg.
Aislamiento acústico
Normalizado (R): 6 lb/pies3
15dBA - 12 lb/pies3 : 20 dBA
Curva STC:20.
Conductividad térmica
0.25 BTU.plg./hr.pies2 ºF a 100 ºF.
Dimensiones
0.61 x 1.22 m.
Densidad calculada de la muestra
21.61 kg/m3.
Frescasa
Figura 14 Frescasa [28].
Fabricada a partir de fibra de vidrio por FiberGlass, es una manta de celda abierta
que permite la absorción de sonido (Figura 14); es incombustible, liviana,
inorgánica y posee dimensiones estables, es usado como aislante acústico,
térmico, y como barrera de vapor [28], las especificaciones técnicas pueden
observarse en la Tabla 2. La Frescasa utilizada para la investigación no disponía
de ningún tipo de recubrimiento.
46
Tabla 2 Frescasa, especificaciones técnicas del fabricante.
Coeficiente de reducción de ruido NRC).
0.85(2.5”)
Resistencia térmica (°F.ft2.h/BTU)
R= 8
Dimensiones
15,24m (600*) Largo
x 1.22m (48”) Ancho
x 3.5” y 2.5” Espesor
Densidad calculada de la muestra
2.98 kg/m3
Black Theater
Figura 15 Black Theater [28]
Está compuesto por un cuerpo de fibra en fibra de vidrio aglomerada con resina
termo-resistente y un acabado en refuerzo de fibra de vidrio (Figura 15). Tiene
propiedades de aislamiento acústico y térmico, es liviano, de color negro y con
textura uniforme. Es usado para instalarse como cielo raso y como sistemas de
cielo raso metálico de celda abierta [28], para el desarrollo de la investigación, se
usaron los dos espesores disponibles del material (1” y 2”), las especificaciones
técnicas están disponibles en la Tabla 3.
47
Tabla 3 Black Theater, especificaciones técnicas del fabricante [28].
Coeficiente de reducción de ruido
0.7 (1”)
(NRC).
1 (2”)
Conductividad térmica
0.23h ºF.ft 2/BTU
0.033 W/ºC.m2
96”x 48”x 1”
Dimensiones
96”x 48”x 2”
Densidad calculada de la muestra
13.72 kg/m3 (1”)
8.55 kg/m3 (2”)
Acustifibra
Figura 16 Acustifibra [28].
Utilizada para aislamiento y acondicionamiento acústico en forma de láminas
(Figura 16), diseñada especialmente para espacios internos. Tiene propiedades de
aislamiento acústico y resistencia térmica [28], las especificaciones del fabricante
se exponen en la Tabla 4.
Posteriormente se procedió a la elección del material de uso alternativo para la
caracterización y evaluación teniendo en cuenta las características físicas
necesarias para la absorción del sonido. Se buscaba un material fibroso o poroso;
en el caso de que fuera fibroso, con las fibras lo suficientemente juntas y delgadas
48
para que se produjera fricción; y en el caso de materiales porosos, con los poros lo
suficientemente abiertos y canales interconectados para que se originara
absorción de la energía sonora.
Tabla 4 Acustifibra, Especificaciones técnicas del fabricante [28].
Coeficiente de reducción de ruido (NRC).
0.7 (1”)
0.9 (1.5”)
Dimensiones
2.44mx 1.22m
Espesores de 1.5” y 1”
Densidad calculada de la muestra
32.43 kg/m3
Se contactaron diferentes semilleros de investigación de distintas instituciones que
tienen que ver con el desarrollo y tecnología de materiales en búsqueda de una
posible colaboración:
Centro de Investigación, Innovación y Desarrollo de Materiales (CIDEMAT)
- Universidad de Antioquia.
Ciencia y tecnología de los materiales – Universidad Nacional.
Instituto de capacitación e investigación del caucho y del plástico.
Grupo de investigación de Nuevos materiales (GINUMA) – Universidad
Pontificia Bolivariana.
Se trabajó en conjunto con el Grupo de Investigación de Nuevos Materiales de la
Universidad Pontificia Bolivariana, ya que disponía de un departamento encargado
del estudio y desarrollo de materiales textiles, en el cual se estaba desenvolviendo
una tesis basada en la búsqueda de un material que pudiera ser aplicable para el
desarrollo de un panel acústico que iba a ser ubicado en ambientes hospitalarios.
Debido al lugar de instalación, se presentaban varios requerimientos que limitaban
el uso de materiales acústicos tradicionales; por esa razón, para la evaluación y
caracterización, se eligieron los materiales textiles que se estaban estudiando en
dicho grupo de investigación(Tabla 5).
49
La segunda fase consistió en analizar los resultados de la medición del coeficiente
de absorción y seleccionar solamente un material que cumpliera con un
comportamiento similar al de los materiales acústicos absorbentes tradicionales.
Posteriormente se consideró la contribución frecuencial al nivel de la voz y la
inteligibilidad de la palabra (Figura 17) para tener una visión clara de los
requerimientos necesarios para la evaluación del material en la aplicación que se
estaba estudiando. A continuación se presentan las 4 propuestas de los materiales
textiles (Tabla 5), para dichos materiales también se calculó una densidad
aproximada de las muestras disponibles:
Tabla 5 Propuestas de materiales textiles para la caracterización.
Material
Figura
Estrobel
Densidad calculada de la
muestra: 33.82 kg/m
3
Spacer
Densidad calculada de la
muestra: 23.87 kg/m
3
Sándwich de D30 con
Estrobel en el centro
Densidad calculada de la
muestra: 14.72 kg/m
3
Sándwich de D30 con
Estrobel en los extremos.
Densidad calculada de la
muestra: 14.32 kg/m
3
50
Figura 17 Contribución frecuencial al nivel de la voz y la inteligibilidad de la palabra [29].
6.2 Medición del coeficiente de absorción por el método del tubo de onda
estacionaria
Posterior a la selección de los materiales a caracterizar, se realizó la medición del
coeficiente de absorción por el método de tubo de onda estacionaria basado en el
estándar internacional ISO 10534-1 / ASTM C384 “Acústica – Determinación del
coeficiente de absorción e impedancia en tubos de impedancia. Parte 1: Método
de la tasa de ondas estacionarias”.
La medición se realizó en el laboratorio de acústica de la Universidad de San
Buenaventura Medellín (Figura 18), como primer paso se determinó el nivel de
ruido continuo equivalente dentro del tubo (56 dB en ponderación Z) para
asegurarse que el nivel de presión de las medidas lo sobrepasaran 10 dB.
Posteriormente, se procedió a instalar la muestra en el equipo de medición; se
tomaron datos de nivel de presión sonora y distancia en un mínimo y un máximo
de presión en el tubo para diferentes frecuencias dentro del rango de trabajo,
51
consecutivamente dichos datos fueron utilizados para el cálculo del coeficiente de
absorción del material a medir usando las ecuaciones (38), (39) y (40).
Los resultados se presentan por bandas de tercios de octava, se obvian
mediciones en la frecuencia de 630 Hz debido a anti-resonancias presentadas en
el sistema, para más detalles ver el Anexo A.
Herramientas utilizadas en la medición:
Muestra del material a medir.
Tubo de impedancias.
Sonómetro 01 dB Solo Blue.
Amplificador de potencia Crown XLS-202.
Interfaz de audio M-audio Mobil Pro.
Flexómetro.
Generador de señales a partir del software Reaper.
Figura 18 Montaje de la medición, tubo de impedancia.
En la Figura 19 se expone el diagrama de bloques de la configuración de los
equipos usados para la medición.
52
Generador de
señal:
Computador
portátil con
sofware
Reaper
Interfaz de
Audio
Amplificador
de potencia
Tubo de
impedancias:
Excitación de
los altavoces.
Sonómetro:
NPS de los
mínimos y
máximos de
presión.
Figura 19 Diagrama de flujo - Medición del Coeficiente de absorción a incidencia normal.
6.3 Diseño y construcción del tubo de onda estacionaria para la medición de
resistencia al flujo
Para la medición de resistencia al flujo por el método de Ingard y Dear, es
necesario un montaje especial basado en el tubo de impedancias, por lo que se
decidió entonces diseñar y construir el montaje requerido. Los autores proponen
dos condiciones que delimitan las dimensiones del tubo de acuerdo al rango de
frecuencias de trabajo, teniendo en cuenta lo anterior, se calcularon la longitud y el
diámetro del tubo siguiendo las ecuaciones (41) y (42), obteniendo un tubo con las
siguientes dimensiones:
Longitud: 1.71 m
Diámetro: 5 cm.
Se calcularon para, obtener un tubo que midiera la Resistencia al flujo de 100 Hz y
sus múltiplos impares hasta 4000 Hz de acuerdo a su diámetro. Como material
para la construcción, se eligió PVC, pues cumplía con la rigidez y dimensiones
requeridas, además de ser favorable económicamente. El tubo se partió en dos
secciones, la primera de 0.85 m y la segunda de 0.86 m como se muestra en la
Figura 20.
53
Figura 20 Secciones del tubo.
Se requería un porta-muestras donde fuera posible variar el espesor del material
sin afectar la longitud L que tenía que ser constante para cumplir las condiciones
propuestas por los autores. Dicho porta-muestras se elaboró en acrílico y
constaba de un cilindro de 6 cm de diámetro y 15 cm de largo donde se ubicaba la
muestra y se insertaba la segunda sección del tubo a presión hasta el final de la
muestra (Figura 21). También disponía de una brida para unir las dos secciones
del tubo.
Figura 21 Porta-muestras
54
Para la fuente, se tenía que garantizar la emisión de ondas homogéneas y planas,
por lo que se planteó un diseño de una caja acústica con dos altavoces
enfrentados, un volumen en el centro y
un volumen para cada uno de ellos
(Figura 22). La caja se construyó a base de MDF de 15 mm de espesor, y los
altavoces fueron de 6 pulgadas y 6 Ohmnios.
Figura 22 Fuente
La ubicación de los micrófonos estaba definida; el micrófono 1 debía ir antes de la
muestra (al final de la primera sección del tubo), y el micrófono 2 justo antes de la
terminación rígida en la segunda sección del tubo. Para la terminación rígida se
usó un tapador para tubos de PVC a la medida (Figura 23), debido a la rigidez del
mismo, el agujero para la ubicación del segundo micrófono tuvo que hacerse
antes, quedando a una distancia considerable de la terminación rígida, por lo que
se propuso insertar una pieza circular de madera con un grosor de 5 cm para
lograr que la terminación rígida quedara justo después del micrófono 2, esto
generó que la longitud efectiva del tubo variara, quedando un poco más corto de lo
diseñado (Figura 23 y Figura 24).
55
Figura 23 Tapón terminación rígida.
Figura 24 Tubo Finalizado.
56
Se diseñó un código en el software MatLab para el procesamiento de las señales
obtenidas de los micrófonos y la obtención de los datos de resistencia al flujo de
los materiales seleccionados, ver Anexo C. En la Figura 25 se presenta un
diagrama de bloques del procesamiento desarrollado para la obtención de los
datos:
Figura 25 Diagrama de flujo del algoritmo utilizado para el procesamiento de la señal.
57
Al algoritmo entran 4 señales que corresponden a la captura de los dos micrófonos
en una posición inicial y la captura de los mismos micrófonos posterior a un
intercambio de posiciones. El código obtiene la función de transferencia entre los
dos micrófonos para cada posición y posteriormente determina la función de
transferencia a partir de las halladas previamente. Finalmente a partir de dicha
función, se obtiene el valor de resistencia al flujo normalizada para la muestra
medida. Se presenta a continuación el pseudocódigo del proceso.
6.3.1 Pseudocódigo
Inicio
Importar datos capturados del micrófono 1 en la posición 1
Importar datos capturados del micrófono 2 en la posición 1
Importar datos capturados del micrófono 1 en la posición 2
Importar datos capturados del micrófono 2 en la posición 2
Cálculo de función de transferencia H12_1 posición 1
Cálculo de función de transferencia H12_2 posición 2
Cálculo de H12K función de transferencia corregida
Establecer la frecuencia de muestreo
Normalización del eje en frecuencia
Cálculo de la impedancia al flujo normalizada
Cálculo de la resistencia al flujo
Gráfico de resistencia al flujo
6.4 Medición de resistencia al flujo por el método de Ingard y Dear.
Posterior a la construcción del tubo de onda estacionaria para la medición de
resistencia al flujo por el método de Ingard y Dear, se procedió a ejecutar la
medición de los materiales seleccionados y previamente cortados a la medida.
La medición se realizó en la sala de grabación del Estudio A de la Universidad de
San Buenaventura Medellín (Figura 26), se instaló la muestra del material y se
ubicaron los micrófonos en la primera posición, posteriormente se generó una
58
señal de ruido blanco, elegida debido a la equivalencia energética presente en
todas las frecuencias, y se procedió a realizar la captura de los dos canales con
una duración de 10 segundos. Seguidamente, se intercambió la posición de los
micrófonos y se realizó otra captura generando la misma señal en la fuente, que
junto con las dos primeras se procesaron en el código previamente desarrollado
para obtener el valor de resistencia al flujo para la muestra medida.
Figura 26 Medición Material: Acustiplaca.
Herramientas utilizadas en la medición:
Muestra del material a medir.
Tubo de onda estacionaria.
2 micrófonos dbx RTA.
Interfaz de audio M-box 3.
Amplificador de potencia Crown XLS-202.
Software de captura y generador de señal ProTools.
Computador portátil Mac Book Pro.
Software MatLab.
59
En la Figura 27 se presenta el diagrama de flujo de la configuración de los equipos
usados para la medición.
Figura 27 Diagrama de flujo - Medición resistencia al flujo.
7. RESULTADOS
7.1 Coeficiente de absorción por el método del tubo de onda estacionaria
En esta sección se presentan los resultados de la medición del coeficiente de
absorción a incidencia normal por el método del tubo de onda estacionaria. Los
resultados se exponen en gráficos de frecuencia contra coeficiente de absorción,
uno para los materiales tradicionales (Figura 28) y otro para los materiales textiles
propuestos (Figura 29).
60
Figura 28 Coeficiente de absorción a incidencia normal de los materiales tradicionales.
Figura 29 Coeficiente de absorción a incidencia normal de los materiales textiles propuestos.
61
7.2 Resistencia al flujo por el método de Ingard y Dear.
Posterior al procesamiento de las señales capturadas, se obtienen gráficos como
el que se muestra en la Figura 30, donde los valores de resistencia al flujo
normalizada están determinados por los picos presentes en las frecuencias que
cumplen con la condición establecida por los autores en la Ecuación (43).
Se seleccionaron valores hasta 1100 Hz para materiales de 1 pulgada de espesor
y hasta 900 Hz para materiales de 2 pulgadas de espesor ya que de acuerdo con
los autores, a frecuencias bajas los efectos de la reactancia son despreciables en
comparación a la resistencia, y la velocidad de partícula se considera constante a
través del material. Se pude observar que los efectos de la reactancia comienzan
a presentarse a partir de 1300 Hz para los materiales de 1 pulgada y en 1100 Hz
para los materiales de 2, esto se evidencia porque los valores picos de las gráficas
muestran un corrimiento, presentándose en valores de frecuencia que no cumplen
con la condición establecida por la Ecuación (43).
Seguidamente se calculó el valor de resistencia al flujo normalizada característico
de cada material haciendo un promedio de los datos obtenidos de todas las
frecuencias, y con dicho valor, se obtuvo la resistividad del material, esta última
necesaria para el cálculo de la impedancia característica y para el coeficiente de
absorción, los resultados son presentados en la Tabla 6.
62
Figura 30 Determinación de los valores de Resistencia al Flujo normalizada para las frecuencias que
cumplen la condición del cuarto de longitud de onda.
Tabla 6 Valores de Resistencia al flujo, Resistencia específica y Resistividad para cada uno de los
materiales.
Material
Resistencia al flujo
Resistividad
normalizada
(Rayls/m)
Acustiplaca
3.51
25905.08
Black Theater 1”
0.79
12625.07
Black Theater 2”
1,5
10497.93
Acustifibra
2.64
42190.11
Frescasa
0.68
5488.04
Spacer
0.8
12784.88
Spacer con cubierta
0.87
13903.56
63
8. ANÁLISIS DE RESULTADOS
Medición del coeficiente de absorción
Al observar los resultados de la medición del coeficiente de absorción a incidencia
normal de los materiales seleccionados (Figura 28 y Figura 29), se observa una
tendencia parecida para los materiales tradicionalmente usados en soluciones
acústicas, con poca absorción en frecuencias bajas pero que tiende a aumentar a
medida que lo hace la frecuencia. Para el caso de la Acustiplaca el
comportamiento difiere de lo común en 2500 Hz, donde el coeficiente de absorción
decrece en vez de aumentar o estabilizarse, y presenta mejor absorción en
frecuencias bajas en comparación con los otros materiales, lo que puede atribuirse
al proceso de fabricación y a la materia prima, la cual es diferente al de los demás
materiales que son desarrollados a partir de fibra de vidrio.
Se advierte la influencia del espesor en la absorción a bajas frecuencias, para las
muestras de mayor espesor (Acustiplaca, Frescasa y Black Teather 2”), la
absorción en este rango es más grande con respecto a las muestras de menor
espesor (Acustifibra y Black Teather 1”). Ahora haciendo una comparación entre el
Black Theater de 1 pulgada y el de 2 pulgadas, se nota una aumento en la
absorción a bajas frecuencias en el espesor de 2 pulgadas, en este caso no tan
considerable, sin embargo el aumento de espesor contribuye considerablemente
la absorción en frecuencias de 800 Hz a 2000 Hz, la cual crece hasta un 20%.
Observando las tendencias de los materiales textiles propuestos, en el caso del
los valores de coeficiente de absorción para las diferentes frecuencias no
sobrepasan de 0.6, siendo ésta la máxima absorción presentada solo para la
frecuencia de 1 kHz; sin embargo, la combinación de este material junto con la
espuma D30 en sus diferentes presentaciones, manifiestan valores de absorción
mayores y similares entre si, siendo mejores en el Sándwich con Estrobel en el
medio
para las frecuencias de 500 a 1600 Hz. Como observación, dicha
64
combinación responde efectivamente en frecuencias medias pero presenta una
deficiencia en frecuencias altas. La tendencia obtenida difiere considerablemente
de las presentadas en los materiales tradicionalmente utilizados.
Con respecto al Spacer, presenta un comportamiento comparable al
de un
material poroso absorbente (Figura 31), el cual no es tan efectivo absorbiendo
energía en frecuencias bajas, pero a medida que aumenta la frecuencia, su
desempeño es superior. Para este caso, desde 1250 Hz en adelante. Por esta
razón se elige este material para su utilización como material alternativo a los
materiales tradicionales desarrollados a partir de fibras minerales.
Figura 31 Comparación del coeficiente de absorción del Spacer con el Black Theater de 1 pulgada.
65
Comparación del coeficiente de absorción calculado con el modelo de Allard
y Champoux contra los resultados de la medición del coeficiente de
absorción por el método del tubo de impedancias.
Haciendo un análisis de los gráficos obtenidos después de calcular el coeficiente
de absorción a partir de la resistividad con el modelo de Allard y Champoux, se
estudia la similitud con la absorción obtenida en la medición. Comenzando con el
black theater (Figura 32), presenta una tendencia calculada próxima a la absorción
medida para la muestra de una pulgada de espesor, siendo coincidente en el valor
de absorción para 500 Hz. En el caso de la muestra de 2 pulgadas de espesor
(Figura 33), la tendencia obtenida es similar a la medida para frecuencias altas,
coincidiendo en 2500 Hz, sin embargo se observa sensibilidad al espesor en el
modelo utilizado, ya que la absorción calculada para el de 2 pulgadas está sobre
estimada en bajas frecuencias, lo cual no se le atribuye a la resistividad, pues es
de saber que ambas muestras del material tienen un valor similar (12784.88
rayls/m para el de 1” y 10497.93 rayls/m para el de 2”) y para el espesor de 1” no
existe tal comportamiento.
Figura 32 Coeficiente de absorción para el Black Theater 1.
66
Figura 33 Coeficiente de absorción para el Black Theater 2”.
Pasando a la Acustifibra (Figura 34), se advierte que los comportamientos son
coincidentes, teniendo valores casi iguales de absorción para las frecuencias de
500 y 1250 Hz, sin embargo para las frecuencias más altas, se observa un
incremento, el cual puede deberse al valor de resistividad (42190.11 rayls/m). En
frecuencias bajas se presenta una absorción deficiente con respecto a la medida
lo que puede estar relacionado al espesor que tiene la muestra y que afecta al
modelo de esa manera.
Para la Frescasa (Figura 35), se observa que el modelo presenta una absorción
superior en bajas frecuencias, lo cual sugiere que el comportamiento del modelo
en dicho rango está determinado por el espesor. En altas frecuencias, la tendencia
es afectada por el valor de la resistividad. en este caso, el modelo de la Frescasa
presenta una pequeña disminución en la absorción de las frecuencias altas con
respecto a lo medido, esto puede deberse a que presenta el valor más pequeño
de resistividad (5488.04 rayls/m).
67
Figura 34 Coeficiente de absorción para la Acustifibra.
Figura 35 Coeficiente de absorción para la Frescasa..
68
En la Acustiplaca (Figura 36), se observa que la absorción calculada tiene una
forma similar a la medida, sin embargo difiere en los valores, siendo superiores en
la tendencia calculada para todo el rango de frecuencia, lo cual se debe a su gran
espesor y
a su valor de resistividad, que es uno de los mas considerables
(25905.08 rayls/m).
Figura 36 Coeficiente de absorción para la Acustiplaca.
De acuerdo con lo mencionado, se observa que el modelo es afectado en gran
medida por el espesor del material y no tanto por el valor de la resistividad. En
bajas frecuencias el comportamiento está casi definido por el espesor del material,
pues se ve que a mayores espesores la absorción es mucho mayor con respecto a
los valores medidos. A altas frecuencias el valor de resistividad comienza a
influenciar la correspondencia de la predicción con la medición.
A valores altos de resistividad y espesores grandes, la absorción crece tendiendo
al valor de la unidad, mientras que a espesores grandes y resistividad pequeña, la
tendencia decrece poco y solo a altas frecuencias. A espesores pequeños y
69
resistividad intermedia, el comportamiento parece ser casi lineal. A espesores
pequeños y resistividad grande, la tendencia crece pero solo a altas frecuencias,
mientras que a bajas mantiene un comportamiento casi lineal.
Las demás variaciones entre las absorciones calculadas y las absorciones
medidas, pueden deberse a que los valores de porosidad y tortuosidad no sean
los mismos ni sean cercanos a la unidad para todos los materiales como lo asume
el modelo, además de que existe la posibilidad de que éstos materiales difieran
en sus características físicas con respecto a los incluidos en la muestra de
materiales utilizada para el desarrollo del modelo.
Influencia de la resistividad en el coeficiente de absorción.
Ahora con base en las tendencias de absorción obtenidas de la medición y los
valores de Resistividad medidos (Tabla 6), se analiza la influencia que tiene la
resistividad en el coeficiente de absorción. Para la Acustifibra y Acustiplaca que
tienen valores de absorción medidos inferiores a 0.8 en altas frecuencias, la
Resistividad puede jugar un papel importante en la justificación de dicho
comportamiento. Cabe anotar que ambos materiales son los que presentan
mayores valores de resistividad,
lo que puede estar relacionado con que la
absorción no sea tan superior como lo es para otros materiales debido a que la
oposición al paso de la onda es tan grande que comienza a presentarse un mayor
coeficiente de reflexión.
Valores intermedios de Resistividad como los presentados en el Black Theater de
1” y el Spacer, resultan convenientes para una buena absorción del material; es
posible notar que a altas frecuencias la absorción es mayor.
De acuerdo con la teoría, a valores pequeños de resistividad, se presenta poca
absorción, pero si se observa la tendencia de la Frescasa y su valor de
resistividad, es posible observar un comportamiento que no coincide con lo que se
70
establece en la teoría, pues presenta valores de absorción muy superiores para
tener el valor resistividad más pequeño de todos los materiales medidos.
8.1 Evaluación de la aplicación acústica del material alternativo.
Como se mencionó, este proyecto de investigación estaba trabajando en
colaboración con el Grupo de Investigación de Nuevos Materiales de la
Universidad Pontifica Bolivariana, donde se estaba realizando una tesis de
maestría que como objetivo general pretendía diseñar un panel acústico
absorbente para implementarlo en las salas de urgencia de los hospitales, esto
con el fin de mitigar el ruido generado por las voces de las personas que acuden a
dicho espacio y aumentar la privacidad. Al tratarse de un entorno hospitalario, se
presentan varias restricciones a la hora de la implementación, entre las cuales
está prohibido el uso de materiales como los tradicionalmente usados en
soluciones acústicas, pues se requieren materiales
y superficies que sean
lavables con el fin de conservar un ambiente aséptico. Después de la evaluación
de los materiales textiles propuestos y la elección del material con el
comportamiento más similar a los materiales tradicionalmente usados para
soluciones acústicas, se analizó entonces el uso de la cubierta tipo plástico
perforado en el material alternativo a implementar (Figura 37).
71
Figura 37 Efecto de la cubierta en la absorción del Spacer.
Como se puede observar, el uso de la cubierta favorece considerablemente la
absorción del Spacer en frecuencias medias altas, entre 1000 y 2000 Hz, pero
afectó la tendencia para 2500 Hz, cambiando el comportamiento que debería tener
un material poroso y pareciéndose un poco al de un resonador, lo cual puede
deberse al sistema que conforman los hoyos de la cubierta y el espacio de aire
que queda entre la misma y el material, que es similar al de un panel absorbente
tipo resonador con varios orificios. A frecuencias bajas la absorción sigue siendo
deficiente. El incremento de la absorción está relacionada con el aumento de la
resistividad (13903.56 rayls/m), lo que sugiere que el crecimiento de dicha
cantidad favorecerá la absorción hasta cierto punto, ya que después será tan
grande que habrá mucha oposición al paso y la energía sonora no se disipará sino
que se reflejará.
Ahora, teniendo en cuenta lo anterior y conociendo el rango de frecuencias de la
voz humana y las frecuencias que aportan nivel a la misma (Figura 17), se
72
observa que la mayor contribución energética se presenta para la frecuencia de
500 Hz, y conociendo la absorción del material alternativo y la cubierta, es posible
decir que tal configuración no absorbería en gran medida el nivel de la voz
generado. Sin embargo, sabiendo que el sistema se comporta como un absortor
tipo resonante y conociendo la ecuación del comportamiento de un panel
absorbente tipo resonador con varios orificios (Ecuación (54)), puede proponerse
una cubierta más gruesa, con un espacio de aire mayor entre el material y la
misma y con orificios un poco más grandes, para mover la frecuencia de
resonancia hasta un rango donde sea útil para la absorción de dicha banda. Es
importante resaltar que se trata de un material que tiene un buen desempeño
como absorbente en frecuencias específicas, pero esto no garantiza que al usarlo
en el panel, tenga un buen nivel de aislamiento entre dos espacios, ya que para
esto existen otros factores que afectan, como la masa del panel, la distancia entre
las fuentes, la instalación como tal del panel, las dimensiones de la sala, el tiempo
de reverberación, entre otros [30].
√
donde
(54)
es la suma de las secciones transversales de los orificios en cm 2,
espesor del panel en cm,
es el
3
es el volumen de la cavidad en cm [29].
Otra alternativa en la aplicación acústica del Spacer es el uso de paneles para el
aumento de la privacidad del mensaje, es posible ver en la Figura 17 que las
frecuencias altas son las más contribuyentes a la inteligibilidad de la palabra,
especialmente la banda de 2 kHz, para la cual el material presenta una absorción
de 0.9. Esto puede ser útil en acondicionamientos de oficinas abiertas, donde la
privacidad del mensaje juega un papel importante en la concentración y
productividad [30].
73
9. CONCLUSIONES
El valor de resistividad o resistencia específica al flujo por unidad de espesor, puede
relacionarse con la absorción de un material, sin embargo no describe totalmente su
comportamiento. Para una descripción completa de la absorción, son necesarios los
valores de las otras cantidades que la afectan directamente como la tortuosidad y la
porosidad. Esto se pudo observar al hacer uso del modelo para materiales acústicos
de Allard y Champoux, que determinaba la absorción de un material ingresando solo
los valores de espesor y resistividad del material; el modelo presentaba resultados
muy sensibles al espesor, y el valor de resistividad solo afectaba la tendencia a altas
frecuencias. Ahora, con referencia a los valores de resistividad y el coeficiente de
absorción medido, no es posible determinar qué tan bueno es un material absorbiendo
energía sonora únicamente a partir del valor de resistividad, pues dicho valor no
proporciona información detallada del comportamiento del material.
El método de medición de Ingard y Dear es una alternativa de construcción sencilla y
costos reducidos para determinar la resistencia al flujo de un material, sin embargo es
importante tener consideraciones para una adquisición de datos confiable que
favorezca el análisis, tales como un nivel apropiado de la fuente y la correcta
instalación del montaje en el momento de la medición.
El valor de resistividad de un material es útil para múltiples aplicaciones en soluciones
acústicas, lo que determina la importancia de su medida en la caracterización de un
material.
El material alternativo es comparable en términos de absorción acústica frente a los
materiales tradicionales en el mercado Colombiano y podría utilizarse sólo como uno
de los materiales constituyentes del sistema que se busca proponer para el control de
ruido en espacios abiertos.
74
10. LISTA DE TABLAS
Tabla 1 Acustiplaca, Especificaciones técnicas del fabricante. ............................ 46
Tabla 2 Frescasa, especificaciones técnicas del fabricante. ................................. 47
Tabla 3 Black Theater, especificaciones técnicas del fabricante [28]. ................... 48
Tabla 4 Acustifibra, Especificaciones técnicas del fabricante [28]. ........................ 49
Tabla 5 Propuestas de materiales textiles para la caracterización. ....................... 50
Tabla 6 Valores de Resistencia al flujo, Resistencia específica y Resistividad para
cada uno de los materiales. ............................................................................ 63
Tabla 7 Corrección del centro acústico. ................................................................. 83
Tabla 8 Velocidad del sonido dentro del tubo. ....................................................... 84
Tabla 9 Corrección atenuación por viscosidad. ..................................................... 84
75
11. LISTA DE FIGURAS
Figura 1. Interacción de ondas sonoras con una superficie [1]. .................................. 13
Figura 2 Incidencia de una onda plana sobre una superficie infinita con impedancia
uniforme [8] ......................................................................................................... 17
Figura 3 Capa delgada de material absorbente al frente de un espacio de aire
respaldado por una pared rígida. A. Espacio de aire localmente reactivo
(Pariticionado). B. Espacio de aire no particionado. ............................................ 24
Figura 4
Coeficiente de absorción de una capa delgada rígida resistiva al flujo
respaldada por un muro rígido en función de la frecuencia normalizada en forma
de la razón del grosor del espacio de aire y la longitud de onda, contra la
resistencia al flujo normalizada. A. Incidencia normal. B. Incidencia aleatoria para
un espacio de aire con reacción localizada. C. Incidencia aleatoria para un
espacio de aire con reacción no localizada [11]. ................................................. 26
Figura 5 Coeficiente de absorción a incidencia normal de una capa flexible y resistiva
en frente de un espacio de aire [11]. ................................................................... 28
Figura 6 Atenuación en un ducto rectangular recubierto en los lados opuestos.
Reacción Local [10]. ............................................................................................ 30
Figura 7 Coeficiente de absorción para diferentes dispositivos micro-perforados [14].
............................................................................................................................ 31
Figura 8 Dos agujeros adyacentes de un difusor de Schroeder [14]. .......................... 32
Figura 9 Variación del coeficiente de absorción a incidencia normal de un difusor
según la cubierta [14]. ......................................................................................... 33
Figura 10. Tubo de impedancia. Arriba: Montaje con sonda. Abajo: Montaje con dos
micrófonos [15]. ................................................................................................... 34
Figura 11. Montaje Ingard & Dear [18]. ....................................................................... 37
Figura 12 Diagrama de flujo de la metodología........................................................... 44
Figura 13 Acustiplaca [27] .......................................................................................... 45
Figura 14 Frescasa [28]. ............................................................................................. 46
Figura 15 Black Theater [28] ....................................................................................... 47
Figura 16 Acustifibra. .................................................................................................. 48
Figura 17 Montaje de la medición, tubo de impedancia. ............................................. 52
76
Figura 18 Diagrama de flujo - Medición del Coeficiente de absorción a incidencia
normal. ................................................................................................................ 53
Figura 19 Secciones del tubo...................................................................................... 54
Figura 20 Porta-muestras ........................................................................................... 54
Figura 21 Fuente ........................................................................................................ 55
Figura 22 Tapón terminación rígida. ........................................................................... 56
Figura 23 Tubo Finalizado. ......................................................................................... 56
Figura 24 Diagrama de flujo del algoritmo utilizado para el procesamiento de la señal.
............................................................................................................................ 57
Figura 25 Medición Material: Acustiplaca. ................................................................... 59
Figura 26 Diagrama de flujo - Medición resistencia al flujo. ........................................ 60
Figura 27 Coeficiente de absorción a incidencia normal de los materiales tradicionales.
............................................................................................................................ 61
Figura 28 Coeficiente de absorción a incidencia normal de los materiales textiles
propuestos........................................................................................................... 61
Figura 29 Determinación de los valores de Resistencia al Flujo para las frecuencias
que cumplen la condición del cuarto de longitud de onda. .................................. 63
Figura 30 Coeficiente de absorción para la Acustiplaca. ............................................ 69
Figura 31 Coeficiente de absorción para el Black Theater 1. ...................................... 66
Figura 32 Coeficiente de absorción para el Black Theater 2”. ..................................... 67
Figura 33 Coeficiente de absorción para la Acustifibra. .............................................. 68
Figura 34 Coeficiente de absorción para la Frescasa.. ............................................... 68
Figura 35 Comparación del coeficiente de absorción del Spacer con el Black Theater
de 1 pulgada. ....................................................................................................... 65
Figura 36 Efecto de la cubierta en la absorción del Spacer. ....................................... 72
Figura 37 Contribución frecuencial al nivel de la voz y la inteligibilidad de la palabra
[30]. ..................................................................................................................... 51
Figura 38 Nivel de presión sonora dentro del tubo de impedancia para 3 posiciones de
micrófono............................................................................................................. 82
77
12. REFERENCIAS BIBLIOGRÁFICAS
[1] M. Long, Architectural Acoustics.: Elsevier Academic Press, 2006.
[2] I López, "Acústica para la industria," Acústica Arquitectónica, 2003.
[3] J Sommerhoff, Acústica de Locales, Universidad Autral de Chile, Ed. Chile,
1989.
[4] F Everest and Pohlmann, Master handbook of acoustics, 5th ed. USA: Mcgraw
hill, 2009.
[5] L.Beranek and Mellow T, "Acoustics: Sound fields and transducers," Elsevier,
vol. 2, 2012.
[6] L. Beranek, Acoustics. Cambridge, USA: Acoustical Society of America, 1993.
[7] E. Juliá, "Modelización, simulación y caracterización acústica de materiales para
su uso en acústica arquitectónica," Mecánica de los medios continuos y teoría
de estructuras, Universidad Politécnica de Valencia, Alcoy, Tesis de doctorado
2008.
[8] Frank Fahy, Foundations of engineering acoustics. Oxford: Elsevier Academic
Press, 2001.
[9] G.M Montoya and J.C Salazar, "Caracterización Acústica de materiales de
construcción en la industria Colombiana," Fecultad de Ingenierías, Universidad
de San Buenaventura, Medellín, Tesis de grado 2013.
[10] David A. Bies and Colins H. Hansen, Engineering noise control: Theory and
Practice, 3rd ed. London and New York: Spon Press, 2003.
[11] Itsvan L Ver and Leo. Beranek, Noise and vibration contro engineering. New
Jersey, USA: John WIley and Sons, inc, 2006.
[12] D. A. Bies and C. H. Hansen, "Flow Resistance Information for Acoustical
Design," Applied Acoustics, 1980.
78
[13] M.A Picard, P J Solana, and F Urchueguia, "A method of measuring the
dynamic flow resistance and the acoustic measurement of the effective static
flow resistance in stratified rockwool samples," Journal of sound and vibrations,
vol. 3, no. 216, 1998.
[14] Trevor j Cox and Peter D'Antonio, Acoustics Absorbers and Diffusers , 2nd ed.
New York, USA: Taylor and Francis, 2009.
[15] M Möser and J.L Barros, Ingeniería acústica: Teoría y aplicaciones, 2nd ed.
New York, USA: Springer, 2009.
[16] International Standar, ISO 10534-1 / ASTM C384 “Acústica – Determinación del
coeficiente de absorción e impedancia en tubos de impedancia. Parte 1: Método
de la tasa de ondas estacionarias”, 1996.
[17] International
Standar,
ISO
10534
-2/
ASTM
E1050-12
“Acústica
–
Determinación del coeficiente de absorción e impedancia en tubos de
impedancia. Parte 2: Método de función de transferencia”, 1998.
[18] E Juliá, J Alba, R del Rey Tormos, and Ramis J, "Incertidumbre en la medida de
resistencia al flujo con el método de Ingard and Dear," Física aplicada ,
Mecánica de los Medios Continuos y Teoría de Estructuras, Universidad
Politécnica de Valencia, 2006.
[19] K.U Ingard and T.A Dear., "Measurement of acoustic flow resistance," Journal of
sound and vibration., vol. 103, no. 4, pp. 567 - 572, 1985.
[20] F Cózar, "Métodos de ensayo de la resistencia al flujo de materiales
absorbentes
acústicos,"
Universidad
Politécnica
de
Valencia,
Escuela
Politécnica superior de Gandía, Tesis de Máster 2009.
[21] Romina Del Rey, Jesús Alba, Jorge Arenas, and Jaime. Ramis, "Evaluation of
Two Alternative Procedures for Measuring Airflow Resistance of Sound
Absorbing Materials," PAN Archives of acoustics, vol. 38, no. 4, pp. 547–554,
May 2013.
79
[22] M Garai and F. Pompoli, "A simple empirical model of polyester fibre materials
for acoustical applications," Applied Acoustics, vol. 66, pp. 1383–1398, Apr.
2005.
[23] J Ramis, J Alba, R Del Rey, E Escuder, and V.J. Sanchis, "Nuevos materiales
absorbentes acústicos basados en fibra de kenaf," Materiales de construcción,
vol. 60, no. 299, pp. 133-143, Sep. 2010.
[24] J Ramis, J Alba, R Del Rey, E Escuder, and V.J. Sanchis, "Nuevos materiales
absorbentes acústicos obtenidos a partir de restos de botellas de plástico,"
Materiales de construcción, vol. 61, no. 304, pp. 547-558, Dec. 2011.
[25] J Ramis, J Alba, R Del Rey, L Godinho, and J Carbajo, "A model for acoustic
absorbent materials derived from coconut fiber," Materiales de construcción, vol.
64, no. 313, Jan. 2014.
[26] G Almanza and D Lascano, "Diseño, elaboración y medición de un panel
absorbente de sonido con materiales de desecho.," Ingenierías, Universidad de
San Buenaventura , Bogotá, Tesis de Grado.
[27] Calorcol.
http://www.calorcol.com.
[Online].
http://www.calorcol.com/Productos/Cat%C3%A1logodeProductos/tabid/56/Cate
goryID/13/List/1/Level/1/ProductID/27/Default.aspx?SortField=ProductName%2
cProductName
[28] www.fiberglasscolombia.com.
[Online].
http://www.fiberglasscolombia.com/confort-termico-sub-productodetalle.php?tabla=productodetalle1&id=9&pro=AISLAMIENTOS%20TERMO%2
0AC%DASTICOS&id2=15
[29] British Standart, ISO 3382 - Part 3: Acoustics - Measurement of room acoustic
parameters. Open plan offices., 2012.
[30] Antoni. Carrion, Diseño acústico de espacios arquitectónicos. Barcelona,
España: Ediciones UPC.
80
Anexo A: Consideraciones previas a la medición del coeficiente de
absorción por el método del tubo de onda estacionaria.
Debido a inconsistencias presentadas en las primeras mediciones con el tubo de
onda estacionaria disponible en la institución, se tomó la decisión de hacer un
estudio del comportamiento del sistema para posteriormente aplicar las
correcciones necesarias a los resultados obtenidos.
Como primer paso, se verificó el rango de frecuencias de trabajo según la
geometría del tubo [16]; el que está disponible en los laboratorios de la institución
es circular con un diámetro de 8 cm y longitud de 1.5 m, por lo que el rango de
frecuencia útil es:
donde
es la frecuencia superior y
es la frecuencia inferior.
Posteriormente, se realizó la medición con terminación rígida para calcular la
velocidad del sonido dentro del tubo, las correcciones de centro acústico y
atenuaciones por viscosidad como lo recomienda el estándar internacional ISO
10534; durante el desarrollo de dicha medición, se presentó una inconsistencia en
630 Hz, dicha frecuencia no lograba el nivel de presión sonora inicial que se
estaba configurando a pesar del alto nivel de ganancia aplicado a la fuente, debido
a esto, se decidió hacer una medición del espectro en frecuencia dentro del tubo y
de tal manera verificar lo que sucedía en el sistema.
A. 1. Medición del espectro en frecuencia dentro del tubo.
La medición se desarrolló en el laboratorio de acústica de la Universidad de San
Buenaventura Medellín, se generó una señal de ruido blanco con un nivel de 10
dB por encima del ruido de fondo; se hicieron 3 mediciones para posiciones
81
diferentes de micrófono, la primera en la terminación rígida del tubo, la segunda en
la mitad del tubo y la tercera en la caja acústica de la fuente. Los resultados
obtenidos se presentan por bandas de tercios de octava en la Figura 38.
Herramientas utilizadas para la medición:
Sonómetro 01 dB Blue.
Amplificador Crown XLS-202.
Tubo de impedancia.
Generador de señal a partir del software Reaper.
Interfaz de audio Focusrite 2i2
Figura 38 Nivel de presión sonora dentro del tubo de impedancia para 3 posiciones de micrófono.
Se observó una anti-resonancia en la frecuencia de 630 Hz, debido a que el tubo
es un sistema de varios cuerpos acoplados, cada uno con frecuencias de
resonancia presentes y una anti-resonancia entre ellos.
A.2. Correcciones: Medición en terminación rígida
La medición se realizó en el laboratorio de acústica de la Universidad de San
82
Buenaventura Medellín, como primer paso se determinó el nivel de ruido continuo
equivalente dentro del tubo (56 dB en ponderación Z) para asegurarse que el nivel
de presión de las medidas lo sobrepasaran 10 dB. Posteriormente se tomaron
datos de nivel de presión sonora y distancia en dos mínimos y un máximo de
presión en el tubo para diferentes frecuencias dentro del rango trabajo,
consecutivamente dichos datos fueron utilizados para el cálculo de la corrección
del centro acústico (Tabla 7), la velocidad del sonido dentro del tubo (Tabla 8) y la
corrección de atenuación por viscosidad (Tabla 9).
Herramientas utilizadas en la medición:
Tubo de impedancias
Sonómetro 01 dB Solo Blue
Amplificador de potencia Crown XLS-202
Interfaz de audio Focusrite 2i2
Flexómetro
Generador de señales a partir del software Reaper
Tabla 7 Corrección del centro acústico.
Frecuencia (Hz)
250
-0,0012
315
0
400
-0,0014
500
0,0010
800
-0,0018
1000
0,0016
1250
0,0016
1600
0,0011
2000
0,0017
2500
0,00097
83
Tabla 8 Velocidad del sonido dentro del tubo.
Frecuencia (Hz)
(m/s )
250
343
315
346,5
400
343,2
500
346
800
345,6
1000
324
1250
347,5
1600
342
2000
348
2500
345
Tabla 9 Corrección atenuación por viscosidad.
Frecuencia (Hz)
250
-0,0017
315
0
400
-0,003
500
0,002
800
-0,008
1000
0,010
1250
0,012
1600
0,010
2000
0,02
2500
0,014
84
Anexo B: Consideraciones a tener en cuenta en la medición de Resistencia
al flujo por el método de Ingard y Dear.
Después de realizar repetidas veces la medición de resistencia al flujo por el
método de Ingard y Dear, se establecieron varias consideraciones a tener en
cuenta para obtener resultados confiables que faciliten el análisis posterior.
1. Disponer del algoritmo para el procesamiento de la señal al momento de
realizar la medición, esto con el fin de revisar la tendencia obtenida en el
cálculo de la resistencia al flujo.
2. El tamaño de la muestra debe ser tal que al insertarse dentro del tubo no
queden espacios de aire.
3. Contar con equipos confiables: Generador de ruido, interfaz de audio,
software para la captura y micrófonos de medición ojalá de la misma
referencia.
4. En el caso de no disponer de dos micrófonos de medición de la misma
referencia, realizar una calibración ajustando las ganancias de tal manera
que la señal de entrada sea la misma para los dos.
5. No usar niveles altos en la fuente, ya que esto genera distorsión armónica
en las señales que se van procesar y se verá reflejado en el cálculo de la
resistencia al flujo.
6. Ajustar el nivel de la fuente para cada muestra a medir, verificando que las
gráficas de resultados de la medición y el cálculo de la resistencia al flujo
estén lo más limpias posibles.
La Figura 30 Determinación de los valores de Resistencia al Flujo normalizada
para las frecuencias que cumplen la condición del cuarto de longitud de onda.
presenta una señal limpia y apta para el análisis.
85
Anexo C: Algoritmos utilizados para el cálculo de las variables.
C.1. Coeficiente de absorción
%% Determinanción del centro Acústico
freq= [250;315;400;500;800;1000;1250;1600;2000;2500];
Ymin= [34.7 103.3;27.8 82.8; 22
64.9;17.4 52;...
10.9 32.5;9.9 26.1;7.1 21;5.6 16.3;...
4.4 13.1;3.6 10.5]./100;%Valores medidos en terminaciÛn Rigida
delta=(1/2).*(3.*Ymin(:,1) - Ymin(:,2));%Valores de CorrecciÛn
Xmin=[Ymin(:,1)-delta Ymin(:,2)-delta];%Corregido para valores en
terminacion rigida
Yminmat=[]./100;%DATOS DISTANCIAS MINIMOS. PARA EL MATERIAL
Xminmat=Yminmat-delta;
%% Longitud de ONDA Lanbda0
n=2;
m=1;
lambda0=(2./(n-m)).*(Xmin(:,n)-Xmin(:,m));%TERMINACIÓN RIGIDA
c0=lambda0.*freq;
%% Determinación de la Atenuación del tubo por Viscosidad
SPL=[70.8
104.2
70.3;...
70.9
104.1
70.9;...
70.8
104.2
70.2;...
69.5
104.8
70;...
73 104.1
72.4;...
69.8
104 70.5;...
71.3
104 71.9;...
69.6
103.9
70.1;...
70 103.7
70.7;...
69.7
103.4
70.1];%min1 max1 min2 TERMINACIÓN RIGIDA
pref=20*(10^-6);
Presion=pref.*(10.^(SPL./20));
DELTAn=(Presion(:,3)-Presion(:,1))./Presion(:,2);
k0pp=(4./lambda0).*asinh(DELTAn./2);
%% Calculo de la Absorción
SPLmat=[]; ];%min1 max1 MATERIAL
pref=20*(10^-6);
Presionmat=pref.*(10.^(SPLmat./20));
S1=Presionmat(:,2)./Presionmat(:,1);
%Factor de Refleción
r=(exp(2*k0pp.*Xminmat(:,1))).*((S1-exp(k0pp.*(lambda0./4)))./(S1+exp(k0pp.*(lambda0./4))));
Abs=1-r.^2;
figure1 = figure;
axes1 =
axes('Parent',figure1,'YMinorGrid','on','YGrid','on','XScale','log',...
'XMinorGrid','on',...
'XGrid','on');
box(axes1,'on');
86
hold(axes1,'all');
plot(freq,Abs,'Marker','*','LineWidth',2,'Color',[0 0 0]);
xlabel('Frecuencia');
xlim([250 2500])
ylabel('Coeficiente de Absorción');
title('Material');
C.2. Resistencia al flujo normalizada
%% Función de transferencia
x1=wavread('CH11.wav');
y1=wavread('CH12.wav');
x2=wavread('CH22.wav');
y2=wavread('CH21.wav');
H12_1=tfestimate(x1((44100*3):(44100*6)),y1((44100*3):(44100*6)));
H12_2=tfestimate(x2((44100*3):(44100*6)),y2((44100*3):(44100*6)));
H12k=(H12_1.*H12_2).^0.5;
Fs=44100;
f=Fs*(0:1/32768:1-1/32768);
fnorm=f*2*pi/Fs;
%% Resistencia al Flujo
ImpNorm=(1+0i)./H12k ; %Impedancia al Flujo Normalizada
ResFlujo=abs(imag(ImpNorm));% Resistencia al Flujo
ResFlujo=smooth(ResFlujo);
figure1 = figure;
axes1 =
axes('Parent',figure1,'Xscale','log','XMinorTick','on','XMinorGrid','on')
;
box(axes1,'on');
grid(axes1,'on');
hold(axes1,'all');
plot(f(1:length(ResFlujo)),ResFlujo,'LineWidth',2,'Color',[0 0 0]);
xlim([50 2500])
xlabel('Frecuencia (Hz)');
ylabel('Resistencia al flujo (Rayls)');
title(Material');
87
C.3. Impedancia característica y coeficiente de absorción a partir del valor de
Resistividad.
f=[250; 315; 400; 500; 800; 1000; 1250; 1600; 2000; 2500]; %Frecuencia
r= ; %Resistividad
l= ; %Espesor de la muestra
%% Modelo Allard y Champoux
a=(-0.0364).*((1.21.*f)./r).^(-2);
b=(0.1144j).*((1.21.*f)./r).^(-1);
p=1.2+(a-b).^(1/2);
c=29.64j+((2.82.*((1.21.*f)./r).^(-2))-(24.9j.*((1.21.*f)./r).^(1))).^(1/2);
d=21.17j+((2.82.*((1.21.*f)./r).^(-2))-(24.9j.*((1.21.*f)./r).^(1))).^(1/2);
k=101320.*(c./d);
T=(1j*2*pi.*f).*(p./k).^(1/2);
ZcAC=(p.*k).^(1/2);
ZsAC=ZcAC.*coth(T.*l);
%% Coeficiente de absorción
AbsAC=1-((abs((ZsAC-(1.21*343))./(ZsAC+(1.21*343)))).^2);
figure1 = figure;
axes1 =
axes('Parent',figure1,'YGrid','on','XScale','log','XMinorTick','on',...
'XMinorGrid','on',...
'XGrid','on');
box(axes1,'on');
hold(axes1,'all');
xlabel('Frecuencia (Hz)');
xlim([250 2500]);
ylabel('Coeficiente de absorciÛn');
title('Spacer con cubierta');
hold on
semilogx(f,AbsMaterial,'MarkerFaceColor',[0 0
0],'Marker','o','LineWidth',2,...
'Color',[0 0 0]);
hold on
semilogx(f,AbsAC,'MarkerFaceColor',[0 0 0],'Marker','o','LineWidth',2,...
'Color',[0.5 0.5 0.5]);
88
Anexo D: Certificado de calibración del sonómetro 01 dB.
89
90
Anexo E: Ficha Técnica del material alternativo. Spacer.
91