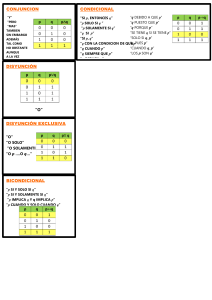
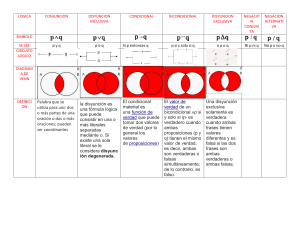
Conjunción (∧) es verdad cuando los 2 son verdad Disyunción fuerte (⊻) es falsa cuando los 2 valores son iguales Disyunción (∨) es falsa cuando las 2 son falsas F⊻F = FALSO V⊻V= FALSO Condicional (⇒) es falso cuando el antecedente es verdadero y el consecuente falso Doble condicional (⟺) es verdadero cuando las 2 preposiciones tienen el mismo valor de verdad V⇒F= FALSO F⟺ F= VERDADERO V⟺ V=VERDADERO Leyes lógicas IDEMPOTENCIA CONMUTATIVA ASOCIATIVA p∧pΞp p∨qΞq∨p p ∨ (q ∨ r) Ξ (p ∨ r) ∨ q P∨PΞP P∧qΞq∧p p ∧ (q ∧ r) Ξ (p ∧ q) ∧ r p⟺qΞq⟺P p ∧ (q ∧ r) Ξ (p ∧ r) ∧ q p⇒qΞq⇒P DISTRIBUTIVA MORGAN LEY CONDICIONAL p ∨ (q ∧ r) Ξ (p ∨ q) ∧ (p ∨ r) ¬ (p ∧ q) Ξ ¬p ∨ ¬q p ⇒ q Ξ ¬p ∨ q p ∧ (q ∨ r) Ξ (p ∧ q) ∨ (p ∧ r) ¬ (p ∨ q) Ξ ¬p ∧ ¬q p ⇒ q Ξ ¬p ⇒ ¬q BICONDICIONAL COMPLEMENTO p ⟺ q Ξ (p ⇒ q) ∧ (q ⇒ P) P ∨ ¬P Ξ V (verdad) p ⟺ q Ξ ¬ (p ⊻ q) P ∧ ¬P Ξ F (falso) IDENTIDAD ABSORCION p∨VΞV p ∧ (q ∨ p) Ξ p p∨FΞp q ∨ (p ∧ q) Ξ q p∧VΞp ¬p ∧ (p ∨ q) Ξ ¬p ∧ q p∧FΞF ¬q ∨ (¬p ∧ ¬q) Ξ ¬q ∨ ¬p ¬p ∧ (q ∨ ¬p) Ξ ¬p q ∨ (¬q ∧ p) Ξ q ∨ p p ∨ (¬q ∧ ¬p) Ξ p ∨ ¬q ¬q ∧ (¬q ∨ p) Ξ ¬q MODUS PONENDO PONENS SIMPLIFICACION a⇒b a∧b a a∨a a a SILOGISMO HIPOTETICO ADJUNCION a⇒b a b⇒c b a⇒c a∧b ADICION MODUS TOLLENDO PONENS a a∨b a⇒b b ¬b ¬b a∨b a ¬a (a ∨ c) (V c) DOBLE NEGACION CONMUTATIVA LEY DE MORGAN ¬(¬a) ≡ a a∧b≡b∨a ¬(a ∧ b) ≡ ¬a ∨ ¬b a ≡ ¬(¬a) a∨b≡b∧a ¬a ∧ ¬b ≡ ¬(a ∨ b) ¬(a ∨ b) ≡ ¬a ∧ ¬b ¬a ∨ ¬b ≡ ¬(a ∧ b) También se puede usar Condicional y su contrarrecíproca: a ⇒ b ≡ ¬b ⇒ ¬a Bicondicional: a ⇔ b ≡ [(a ⇒ b) ∧ (b ⇒ a)] Asociativas: a ∨ (b ∨ c) ≡ (a ∨ b) ∨ c Distributiva: a ∨ (b ∨ c) ≡ (a ∨ b) ∧ (a ∨ c) a ∧ (b ∧ c) ≡ (a ∧ b) ∧ c a ∧ (b ∧ c) ≡ (a ∧ b) ∨ (a ∧ c)