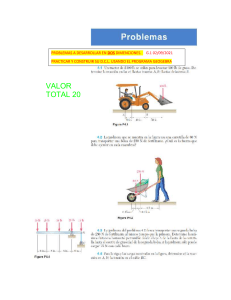
INDICE INDICE ......................................................................................................................... 1 1 INTRODUCCION ................................................................................................... 2 2 Objetivos................................................................................................................ 2 3 4 2.1 Objetivo general ............................................................................................. 2 2.2 Objetivos específicos: ..................................................................................... 2 MARCO TEORICO ................................................................................................ 2 3.1 Modelos Matemáticos ..................................................................................... 2 3.2 La Derivada .................................................................................................... 3 3.3 Razón de Cambio Relacionada ...................................................................... 3 3.4 GeoGebra ....................................................................................................... 3 DESARROLLO ...................................................................................................... 4 4.1 Presentación del Problema ............................................................................. 4 4.1.1 Gráfica del problema ............................................................................... 4 4.1.2 Planteamiento del problema .................................................................... 4 4.1.3 Resolución del problema ......................................................................... 4 4.2 Resolución y Simulación del problema con GeoGebra .................................. 5 4.2.1 Graficación del problema ......................................................................... 5 4.2.2 Planteamiento del problema en la hoja de cálculo de GeoGebra ............ 6 5 CONCLUCIÓN....................................................................................................... 7 6 REFERENCIAS ..................................................................................................... 8 6.1 Bibliografía ..................................................................................................... 8 CIENCIAS EXACTAS MECATRONICA SEDE CUENCA 1 INTRODUCCION El trabajo que se va a desarrolla a continuación tiene como objetivo explicar y comprender el planteamiento y resolución de un problema planteado con anterioridad, el mismo que fue dispuesto por el docente encargado. Donde se expresan y desarrollan temas didácticos y aplicables que se han ido aprendiendo dentro de este tiempo pedagógico impartido por el profesor, como las derivadas y razones de cambio, ocupando datos de variables y funciones. Es así como para dejar en claro cuál es el proceso de funcionamiento de una derivada que se aplica en función de una variable para determinar un dato exacto en cierta situación dispuesta que se podría suscitar en cualquier caso de la vida cotidiana. Es así como el ejercicio número 1 de los proyectos integradores establecidos, siendo este el de la posición de un objeto en razón de cambio a la distancia de otro, es aplicar los procedimientos necesarios para las operaciones pertinentes sin dejar que una falla arruine el proceso. El fin que se desea obtener es el de demostrar cómo la función de derivadas pueden explicar el movimiento de un objeto ante otro de manera exacta y lógica, también se deberá implementar el problema sobre un software para simularlo y resolverlo así también se podrá ingresar diferentes valores en una determinada variable para poder obtener diferentes valores en el resultado y así poder comprobar y evaluar de forma más didáctica y grafica el ejercicio. 2 Objetivos 2.1 Objetivo general Diseñar un a Modelo matemático y con la ejecución de la derivada comprobar resultados reales. 2.2 Objetivos específicos: 3 Identificar fórmulas de distancias y áreas de la figura geométrica resultante de la representación gráfica del problema para relacionarlas entre si y formar el modelo matemático. Aplicar la derivada. Realizar iteraciones modificando la variable de la función encontrada para interpretar la respuesta válida. Realizar conclusiones reales del proceso y solución con la ayuda del programa GeoGebra MARCO TEORICO 3.1 Modelos Matemáticos En ciencias aplicadas y en tecnología, un modelo matemático es uno de los tipos de modelos científicos que emplea algún tipo de formulación matemático para expresar relaciones, proposiciones sustantivas de hechos, variables, parámetros, entidades y 2 CIENCIAS EXACTAS MECATRONICA SEDE CUENCA relaciones entre variables de las operaciones, para estudiar comportamientos de sistemas complejos ante situaciones difíciles de observar en la realidad. El término modelización matemática es utilizado también en diseño gráfico cuando se habla de modelos geométricos de los objetos en dos (2D) o tres dimensiones (3D). El significado de modelo matemático en filosofía de la matemática y fundamentos de la matemática es, sin embargo, algo diferente. En concreto en esas áreas se trabajan con "modelos formales". Un modelo formal para una cierta teoría matemática es un conjunto sobre el que se han definido un conjunto de relaciones unarias, binarias y ternarias, que satisface las proposiciones derivadas del conjunto de axiomas de la teoría. La rama de la matemática que se encarga de estudiar sistemáticamente las propiedades de los modelos es la teoría de modelos. 3.2 La Derivada La derivada es uno de los principales elementos en cálculo; la usamos para resolver una amplia variedad de problemas que incluyen tangentes y tasas de cambio. La derivada de una función mide la rapidez con la que cambia el valor de una función matemática, según cambie el valor de su variable independiente. La derivada de una función es un concepto local, es decir, se calcula como el límite de la rapidez de cambio media de la función en cierto intervalo, cuando el intervalo considerado para la variable independiente se torna cada vez más pequeño. Por ello se habla del valor de la derivada de una función en un punto dado. 3.3 Razón de Cambio Relacionada Una razón de cambio relacionada es una operación matemática donde los datos de una variable en función de “x”, por poner un ejemplo, depende o influye en otras variables, como una variable en función de “y”. se trata de la magnitud que compara dos variables a partir de sus unidades de cambio. en caso de que las variables no están relacionadas tendrán una razón de cambio igual a cero. 3.4 GeoGebra GeoGebra es un software de matemáticas dinámicas para todos los niveles educativos que reúne geometría, álgebra, hoja de cálculo, gráficos, estadística y cálculo en un solo programa fácil de usar. GeoGebra es también una comunidad en rápida expansión, con millones de usuarios en casi todos los países. GeoGebra se ha convertido en el proveedor líder de software de matemática dinámica, apoyando la educación en ciencias, tecnología, ingeniería y matemáticas (STEM: Science Technology Engineering & Mathematics) y la innovación en la enseñanza y el aprendizaje en todo el mundo. 3 CIENCIAS EXACTAS MECATRONICA SEDE CUENCA 4 DESARROLLO 4.1 Presentación del Problema Un hombre está parado en un muelle y jala una lancha por medio de una cuerda. Sus manos están a 3 m por encima del amarre de la lancha. Cuando la lancha está a 4 m del muelle el hombre está jalando la cuerda a una velocidad de 80 cm/s. ¿A qué velocidad se aproxima la lancha al muelle? 4.1.1 Gráfica del problema 4.1.2 Planteamiento del problema ¿Qué se pide en el problema? Se pide calcular la rapidez (velocidad) a la que está disminuyendo la distancia que hay entre la lancha y el muelle, cuando dicha distancia es de 4 m y la longitud de la cuerda esta “disminuyendo” a razón de 0.8 m/s. Es decir, si consideramos que (en cierto instante t) la lancha se encuentra a una distancia x(t) del muelle y z(t) es la longitud de la cuerda, entonces lo que se desea es calcular la rapidez con que cambia (razón de cambio de) la distancia x(t), cuando el valor de x(t) es de 4 m y la razón de cambio de la longitud z(t) de la cuerda es de −0.8 m/s. Esto es se pide calcular a la derivada dx/dt cuando x = 4 y dz/dt = −0.8. [El signo negativo en la razón de cambio de la longitud z(t) de la cuerda se debe a que dicha longitud está disminuyendo (decreciendo). Consideramos el triángulo rectángulo cuyos vértices están en el amarre de la lancha, la base del muelle y las manos del hombre. Este triángulo tiene catetos de longitudes x(t) (distancia entre la lancha y el muelle) y 3m (altura entre la base del muelle y las manos) e hipotenusa de longitud z(t) (longitud de la cuerda). 4.1.3 Resolución del problema Primero: Por el teorema de Pitágoras se cumple que: 4 CIENCIAS EXACTAS MECATRONICA SEDE CUENCA 2 2 𝑍(𝑡) = 𝑋(𝑡) + (3) 2 Donde X(t) y Z(t) dependen del tiempo t. Segundo: Derivando implícitamente con respecto a t se obtiene: 𝑑𝑧 𝑑𝑥 2𝑍(𝑡 ) ( ) = 2𝑥 (𝑡 ) ( ) 𝑑𝑡 𝑑𝑡 Donde, para cualquier instante t ≥0 , mientras x > 0 se tiene que: 𝑑𝑥 𝑧(𝑡) 𝑑𝑧 = ( ) 𝑑𝑡 𝑥(𝑡) 𝑑𝑡 Tercero: En el instante t0 en que x(t0) = 4m se tiene que: 𝑧(𝑡0 )2 = (4)2 + (3)2 a) 𝑧(𝑡0 ) = √(4)2 + (3)2 𝑧(𝑡0 ) = √25 𝑧(𝑡0 ) = 5 Cuarto: debido a que dz/dt = −0.8 m/s, obtenemos que, en ese instante t0: b) 𝑑𝑥 𝑑𝑡 = 𝑧(𝑡) 𝑑𝑧 ( ) 𝑥(𝑡) 𝑑𝑡 𝑑𝑥 5 = (−0,8 𝑚/𝑠) 𝑑𝑡 4 𝑑𝑥 = −𝟏 𝒎/𝒔 𝑑𝑡 4.2 Resolución y Simulación del problema con GeoGebra Para resolver el problema en el software GeoGebra hemos usado el proceso anterior solo que le hemos trabajado únicamente con las fórmulas de los literales a y b. 4.2.1 Graficación del problema Usando los comandos y herramientas del programa se ha dibujado el grafico que representa al problema. Primer comando: Con el comando “polígono” se ha trazado la figura del barco (cuadrilátero: trapecio isósceles invertido y alargado ) y del muelle (figura en forma de L volteada y girada 90º). Segundo comando: Con el comando “segmento de recta” se ha trazado las líneas auxiliares o líneas de referencia “x”, “z” y “tres”. 5 CIENCIAS EXACTAS MECATRONICA SEDE CUENCA Tercer comando: con el comando “deslizador” se lo ha utilizado para hacer que los gráficos tengan movimiento, es decir la figura se mueva hacia el muelle, efecto con el cual se logra determinar la velocidad con la que el barco se acerca al muelle en diferentes distancias. Luego se le ha modificado los puntos y los segmentos de recta para que el grafico la figura trazada se vea despejada y estética. Finalmente de forma adicional se le ha insertado cuatro funciones seno e igualmente se les ha agregado un deslizador para general el efecto de movimiento 4.2.2 Planteamiento del problema en la hoja de cálculo de GeoGebra En las casillas B4 B5 y B6 está especificado el nombre de cada dato que se ocupara en la resolución del problema En la casilla C4 está ingresada la distancia que hay entre el bote y el muelle, esta casilla esta sincronizada con el deslizador X1. En la casilla C5 se calcula el valor de Z mediante el teorema de Pitágoras. Y finalmente en la casilla C6 se obtiene el valor de dx/dt el cual nos dará el valor de la velocidad con la que el bote se acerca el muelle. 6 CIENCIAS EXACTAS MECATRONICA SEDE CUENCA 5 CONCLUCIÓN Se ha Diseñado un Modelo matemático mediante al cual se lo ha derivado comprobar resultados reales y específicos. Para poder obtener el modelo matemático se ha Identificado el teorema de Pitágoras y aplicado a la figura geométrica resultante en la graficación y planteamiento del problema, también se ha realizado iteraciones modificando la variable de la distancia entre el bote y el muelle en la función encontrada para poder interpretar la respuesta válida. En definitiva con este trabajo se ha podido determinar de manera sencilla mediante el programa GeoGebra los resultados obtenidos en la resolución del problema planteado en un inicio, con ello hemos podido visualizar de manera gráfica los resultados del ejercicio e incluso comprobar mediando la hoja de cálculo del programa, también se ha podido ampliar los resultados pudiendo ingresar varias distancias y obtener un resultado con cada una. 7 CIENCIAS EXACTAS MECATRONICA SEDE CUENCA 6 REFERENCIAS 6.1 Bibliografía Definicionabc. (13 de 05 de 2009). definicionabc. Recuperado el 05 de 11 de 2017, de https://www.definicionabc.com/general/ingenieria.php George B. Thomas. (2010). Calculo de una variable. Naucalpan de Juárez, Estado de México: Addison-Wesley. Pursell, V. &. (2007). Calculo. Mexico D.F: PEARSON Education. Ron Larson, B. H. (2010). Calculo de una variable. Mexico D.F: McGRAWHILL/INTERAMERICANA EDITORES, S.A. Stewart, J. (2012). Calculo de una Variable. Mexico D.F: Cengage Learning Editores, S.A. 8