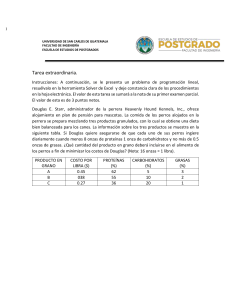
DOCENTE ASIGNATURA EMILIANO GRUESO CARDENAS CÓD. ASIG. P.L INV - OP E- MAIL ACTIVIDAD ESTUDIANTE GRUPO CÓD. EST. PROG. ACADEM. E-MAIL EST. CALIFICACIÓN TALLER 002 FECHA Método Grafico para solucionar Operaciones donde intervienen dos variables, conociendo el modelo de la operación; se identifican las variables definidas, luego la ecuación de la función objetivo y las restricciones a la(s) cual (es) está sujeta la función objetivo. Donde función objetivo se simboliza con la letra z otros autores la representan con la letra c y las variables dentro de las practicas algebraicas comunes se emplea la letra x la letra y en el caso de la Investigación de Operaciones estas variables son representadas por x1 (la cual se lee equis sub uno) que es la misma x y x 2 (equis sub-dos) por y. Ejemplo solucionar por el método grafico la siguiente operación cuyo modelo es. Maximizar z 5x1 4 x2 Sujeto a 6 x1 4 x 2 24 x1 2 x 2 6 x1 x 2 1 x2 2 x1 , x 2 0 Procedimiento: a. Grafique en un plano cartesiano las restricciones. (recuerde que las restricciones son desigualdades, por cada una que grafique debe sombrear la región solución de cada desigualdad). b. Las líneas que limitan las regiones de las desigualdades se cruzan formando un polígono que en su área o superficie encierra todas las soluciones posibles. c. Las (coordenadas) de los puntos del vértice del polígono nos dan las soluciones factibles que puedan maximizar o minimizar a la función objetivo. d. Se toman las coordenadas de los puntos que forman los vértices del polígono y se reemplaza cada uno en la función objetivo obtenido un valor numérico. e. El valor numérico más alto nos indica que las coordenadas que lo hicieron posible es donde está el punto que maximiza la función objetivo. La grafica fue realizada con programa TORA de HANDY TAHA TALLER 02 PARTE A 1. Hallar los valores mínimos y máximos de la función objetivo de acuerdo a la región de la figura; en este caso la función objetivo se simboliza con la letra C, le recuerdo que la podemos simbolizar también con una z (minúscula). 2. Los ejercicios que se proponen a continuación son la formalización de algunas operaciones y se pide que el estudiante halle la solución de la función objetivo a través del Método Gráfico, ya sea maximizando o minimizando según el caso. Max. Min. Max. A. z 3x1 x2 B. z 4 x1 2 x2 C. z 6 x1 3x2 Sujeta a: Sujeta a: Sujeta a: 3x1 4 x 2 12 x1 2 x 2 8 2 x1 3x 2 19 3x1 2 x 2 24 7 x1 2 x 2 28 x1 2 3x1 x 2 15 x1 x 2 4 x2 1 x1 , x 2 0 x1 , x 2 0 x1 0.5 x 2 6.5 D.Min 𝑍 = 60𝑋1 + 80𝑋2 Sujeta a 120𝑥1 + 100𝑥2 ≥ 1000 2𝑥1 + 5𝑥2 ≥ 30 𝑥1 ≥ 0 𝑥2 ≥ 0 E.Min 𝑧 = 6𝑥1 + 𝑥2 Sujeta 3𝑥1 + 𝑥2 ≥ 3 𝑥1 + 5𝑥2 ≤ 15 2𝑥1 + 𝑥2 ≤ 12 𝑥1 , 𝑥2 ≥ 0 TALLER 02 PARTE B ANÁLISIS, FORMALIZACIÓN Y SOLUCIÓN OPERACIONES EMPLEANDO EL MÉTODO GRAFICO. INTRODUCCIÓN La resolución de situaciones problemas exige de un estudiante competencias básicas en lecto-escritura que le permita integrarlos con procesos lógicos para extraer la información de un contexto y llevarla a un proceso de formalización en un modelo de programación lineal, el cual pueda maximizar o minimizar una función objeto de estudio(función objetivo). En este taller el estudiante encontrará unos ejercicios resueltos que le servirán de guía para solucionar el resto que se le proponen, que están en el marco de la Investigación de Operaciones destacando más el contexto de la investigación que el ámbito matemático como tal. La postura mencionada es el escenario propicio para que el estudiante incremente su motivación a la observación y formalización de un proceso que le será de gran ayuda en su ámbito disciplinar. Para plantear y solucionar una operación debe tener en cuenta: a. Realice una lectura a la operación o situación una o dos veces y trate de identificar de que se trata. b. Identifique en la operación cuales son las variables a tener en cuenta y denótelas por: la primera por x1 y la segunda por x 2 y defina cada una a que hace referencia. c. Identifique los elementos o acciones que forman la función objetivo y fórmela. d. Luego identifique las relaciones que dan origen a las restricciones y formalice todas las restricciones de la operación. e. Con la función objetivo y las restricciones se puede proceder a dar la solución de la operación a través del método gráfico. Solucione las operaciones que se proponen a continuación: 1$. Una empresa fabrica dos tipos de productos, el producto X y el producto Y. Para cada producto, es necesario usar tres máquinas diferentes, la maquina A , maquina B y una C. Para manufacturar una unidad del producto X, la maquina A debe usarse durante 3 horas ,la maquina B durante 1 hora y la maquina C durante 1 hora. Para manufacturar una unidad del producto Y se requieren 2 horas en la maquina A, 2 horas en la Maquina B y 1 hora en la maquina C. La utilidad en el producto X es de U$500 por unidad y la utilidad en el producto Y es de U$350 por unidad. La máquina A está disponible durante un total de 24 horas por día, pero la maquina B se puede usar sólo 16 horas y la C 9 horas. Suponiendo que las máquinas están disponibles cuando es necesario. Determinar el número de unidades de cada producto que debe manufacturar cada día para maximizar la utilidad? 2. Un expendido de carnes de la ciudad acostumbra preparar la carne para albondigón o hamburguesa con una combinación de carne molida de res y carne molida de cerdo. La carne de res contiene 80% de carne y 20% de grasa y tiene un costo de $80 por libra ; carne cerdo contiene 68% de carne y el 32% de grasa , y tiene un costo de $60 por libra. ¿Qué cantidad de cada tipo de carne debe emplear la tienda en cada libra de albondigón , si se desea minimizar el costo y mantener el contenido de grasa no mayor de 25%. 3$. En granjas modelo se usa diariamente un mínimo de 800libras de un alimento especial que es una mezcla de maíz y soya, con la composición siguiente por libra de alimento. ALIMENTO PROTEÍNA FIBRA COSTO Maíz 0.09 0.02 0.30 U$ Soya 0.6 0.06 0.90 U$ Las necesidades dietéticas del alimento especial son mínimo de 30% de proteína y un máximo de 5% de fibra. Granjas modelo desea determinar las proporciones de alimento que produzcan un costo mínimo diariamente. 4$. Reddy Mikks produce pinturas para interiores y exteriores, M1 y M2 es la materia prima empleada y se observa en la siguiente tabla: toneladas de materia prima. Ton mat. prima PINTURA EXTERIOR Ton mat prima Disponibilidad PINTURA INTERIORE M1 6 4 24 M2 1 2 6 Utilidad U$ 5 U$ 4 Una encuesta de mercadeo indica que la demanda diaria de pintura para interiores no puede ser mayor que una tonelada más de la pintura para exteriores. También, que la demanda máxima diaria de pintura para interiores es de 2 toneladas. La compañía requiere determinar la mezcla óptima de productos para exteriores e interiores que maximice la utilidad diaria total. 5. Un fabricante de raquetas de tenis obtiene una utilidad de $15 por cada raqueta de tamaño grande y $8 por cada raqueta estándar. Para satisfacer la demanda de compradores, la producción diaria de raquetas estándar debe ser entre 30 y 80 y la producción de raquetas de tamaño grande debe ser entre 10 y 30.Para mantener alta calidad, el número de raquetas producidas no debe de exceder de 80 al día. ¿Cuántas raquetas de cada tipo deben manufacturarse diariamente para maximizar la utilidad? 6. Un fabricante de teléfonos celulares obtiene una utilidad de $25 en un modelo de lujo y $30 en un modelo estándar. La compañía desea producir al menos 80 modelos de lujo y al menos 100 modelos estándar por día. Para mantener alta calidad , la producción diaria no debe exceder de 200 teléfonos .¿cuántos de cada tipo debe producir diariamente para maximizar la utilidad? 7. Dos sustancias, T y S, contienen cada una dos tipos de ingredientes I y G. una libra de S contiene dos onzas de I y 4 onzas de G. una libra de T contiene 2 onzas de I y 6 onzas de G. Un fabricante planea combinar cantidades de las dos sustancias para obtener una mezcla que contenga al menos 9 onzas de I y 20 onzas de G. si el costo de S es $3 por libra y el costo de T es de $4 por libra ¿cuánto de cada sustancia debe usarse para mantener el costo en un mínimo? 8. Una compañía papelera fabrica dos tipos de cuadernos: un cuaderno de lujo con divisiones de temas, que se vende en $ 4 y un cuaderno regular, se vende en $3. El costo de producción es de $3,20 por cada cuaderno de lujo y $ 2.60 por cada cuaderno regular. La compañía tiene las instalaciones para manufacturar entre 2000 y 3000 de lujo y entre 3000 y 6000 cuadernos regulares , pero no más de 7000 en total .¿cuántos cuadernos de cada tipo deben ser manufacturados para maximizar la diferencia entre los precios de venta y los costos de producción? 9$. Una compañía produce bibliotecas y escritorios para los cuales a establecido un precio de venta por unidad de $9000 y $10000 respectivamente. Para la producción de dichos artículos, la compañía cuenta con una disponibilidad mensual de 700 metros de madera, 800 metros de tubo y 900 pliegos de papel de lija. ¿Qué cantidad de bibliotecas y escritorios se deben fabricar mensualmente, si se sabe que una biblioteca consume 7 metros de madera, 10 metros de tubo y 6 pliegos de papel de lija; mientras que el escritorio consume 10 metros de madera, 8 metros de tubo y 15 pliegos de papel de lija? 10$. Un sastre tiene las siguientes materias primas a su disposición: 16 m2 de algodón, 11 m2 de seda y 15m2 de lana. Un traje requiere: 2 m2 de algodón, 1m2 de seda y 1 m2 de lana. Una túnica requiere: 1m2 de algodón, 2m2 de seda y 3m2 de lana. Si el traje se vende en $300 y una túnica en $500. ¿Cuántas piezas de cada confección debe hacer el sastre para obtener la máxima cantidad de dinero?