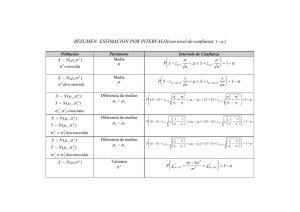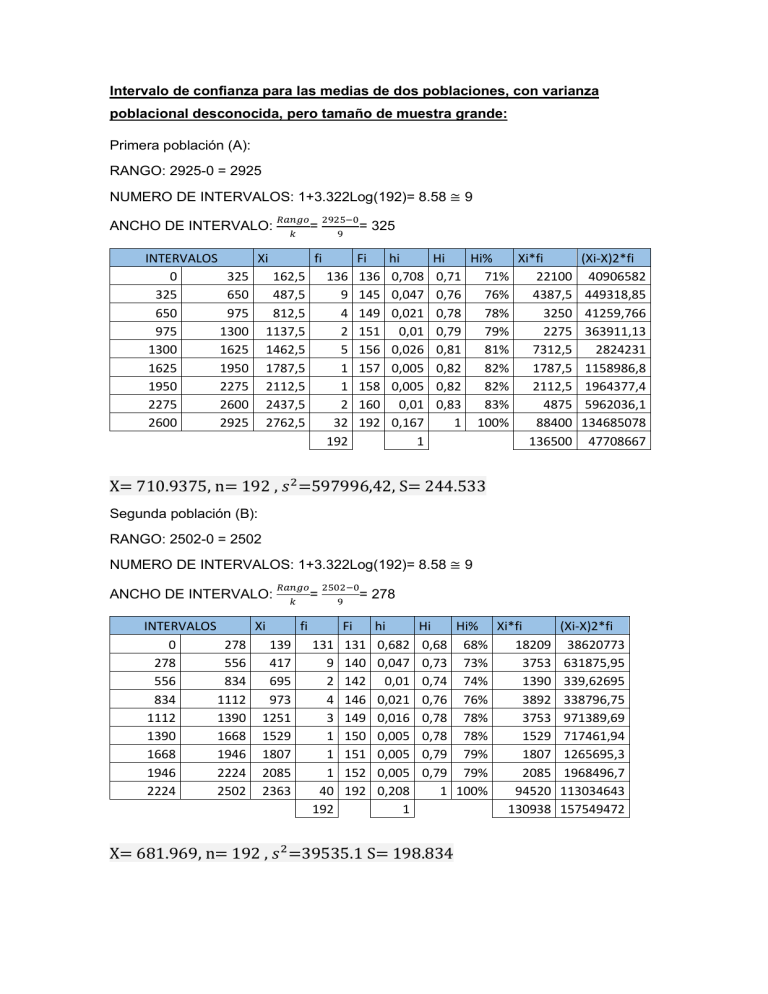
Intervalo de confianza para las medias de dos poblaciones, con varianza
poblacional desconocida, pero tamaño de muestra grande:
Primera población (A):
RANGO: 2925-0 = 2925
NUMERO DE INTERVALOS: 1+3.322Log(192)= 8.58 ≅ 9
ANCHO DE INTERVALO:
𝑅𝑎𝑛𝑔𝑜 2925−0
=
=
𝑘
9
325
INTERVALOS
Xi
fi
Fi
hi
Hi
Hi%
Xi*fi
0
325
162,5 136 136 0,708 0,71
71%
22100
325
650
487,5
9 145 0,047 0,76
76%
4387,5
650
975
812,5
4 149 0,021 0,78
78%
3250
975
1300 1137,5
2 151 0,01 0,79
79%
2275
1300
1625 1462,5
5 156 0,026 0,81
81%
7312,5
1625
1950 1787,5
1 157 0,005 0,82
82%
1787,5
1950
2275 2112,5
1 158 0,005 0,82
82%
2112,5
2275
2600 2437,5
2 160 0,01 0,83
83%
4875
2600
2925 2762,5
32 192 0,167
1 100%
88400
192
1
136500
(Xi-X)2*fi
40906582
449318,85
41259,766
363911,13
2824231
1158986,8
1964377,4
5962036,1
134685078
47708667
X= 710.9375, n= 192 , 𝑠 2 =597996,42, S= 244.533
Segunda población (B):
RANGO: 2502-0 = 2502
NUMERO DE INTERVALOS: 1+3.322Log(192)= 8.58 ≅ 9
ANCHO DE INTERVALO:
𝑅𝑎𝑛𝑔𝑜 2502−0
= 9 =
𝑘
278
INTERVALOS
Xi
fi
Fi
hi
Hi
Hi% Xi*fi
0
278
139 131 131 0,682 0,68 68%
18209
278
556
417
9 140 0,047 0,73 73%
3753
556
834
695
2 142 0,01 0,74 74%
1390
834
1112
973
4 146 0,021 0,76 76%
3892
1112
1390 1251
3 149 0,016 0,78 78%
3753
1390
1668 1529
1 150 0,005 0,78 78%
1529
1668
1946 1807
1 151 0,005 0,79 79%
1807
1946
2224 2085
1 152 0,005 0,79 79%
2085
2224
2502 2363
40 192 0,208
1 100%
94520
192
1
130938
X= 681.969, n= 192 , 𝑠 2 =39535.1 S= 198.834
(Xi-X)2*fi
38620773
631875,95
339,62695
338796,75
971389,69
717461,94
1265695,3
1968496,7
113034643
157549472
Intervalo de confianza para la diferencia de medias:
Se realiza un estudio donde se determinará las medias de las horas realizada por los
estudiantes, por ello se tomaron dos muestras aleatorias con horas medias de 710.9375
y 681.96875 y varianzas de 59796.4174 y 39535.12603 respectivamente. Con un
intervalo del 95% de confianza, hallar la diferencia de las horas medias que tienen los
estudiantes actualmente
1) Nivel de confianza: α= 0.05
𝑍(1−0.05) = 𝑍(0.975) = 1.96
2
2) Reemplazando y calculando los datos en la formula:
59796.4174 39535.12603
µ1− µ2 = {(710.9375 − 681.96875) ± 1.96√
+
}
192
192
0.2371 ≤ µ1 − µ2 ≤ 0.8629
3) Interpretación: Con un nivel de confianza del 95% existe evidencia estadística
para afirmar la diferencia de medias de las postulaciones que realizan los
estudiantes para poder ingresar a un trabajo, la cual está comprendida entre
0.2371 y 0.8629
Tomando en cuenta que u1-u2 no puede ser cero, las postulaciones de los estudiantes
para un trabajo para ambas muestras será diferente.
Intervalo de confianza para la proporción de una población:
En una muestra de 384 estudiantes, se les pregunta cuantas horas de prácticas tienes
hasta el momento y el 79.43% respondió que realizaron un máximo de 350 horas de
practicas. Calcule un intervalo del 95% de confianza para la proporción verdadera de
estudiantes respondieron que realizaron un máximo de 350 horas de practicas.
Variable
X
p
q
[0; 350>
305
0,794
0,206
[350; 700>
23
0,060
0,940
[700; 1050>
15
0,039
0,961
[1050; 1400>
7
0,018
0,982
[1400; 1750>
6
0,016
0,984
[1750; 2100>
17
0,044
0,956
[2100; 2450>
11
0,029
0,971
Datos:
n=384
p=0.794
q=0.206
1) Nivel de confianza: α= 0.05
𝑍(1−0.05) = 𝑍(0.975) = 1.96
2
2) Reemplazando los datos a la formula:
𝟎. 𝟕𝟗𝟒 ∗ 𝟎. 𝟐𝟎𝟔
𝟎. 𝟕𝟗𝟒 ∗ 𝟎. 𝟐𝟎𝟔
𝟎. 𝟕𝟗𝟒 − 𝟏. 𝟗𝟔√
≤ 𝝅 ≤ 𝟎. 𝟕𝟗𝟒 + 𝟏. 𝟗𝟔√
𝟑𝟖𝟒
𝟑𝟖𝟒
𝟎. 𝟕𝟓𝟑𝟓 ≤ 𝝅 ≤ 𝟎. 𝟖𝟑𝟒𝟓
3) Interpretación: Con un nivel de confianza del 95% la verdadera proporción de
estudiantes que fueron contactados solo una vez se encuentra en un intervalo
de 0.7535 a 0.8345
Prueba de hipótesis para la proporción de una población:
Según los estudios anteriores se sabe que la proporción de estudiantes que realizaron
como máximo 350 horas de prácticas es de 0.8345. Para comprobar el estudio se realizó
una muestra de 384 estudiantes de manera aleatoria donde se encuentra que la
proporción que fue contactada es de 0.794. Con un nivel de significancia de 5% ¿Existe
evidencia suficiente para concluir que la proporción de estudiantes que realizaron horas
de prácticas es menor a los estudios anteriores?
Datos:
n = 384 p = 0.794 𝜋 = 0.8345
1) Planteo de Hipótesis:
𝐻0: 𝜋 ≥ 0.8345 (Es mayor que estudios anteriores)
𝐻1: 𝜋 < 0.8345 (Es menor que estudios anteriores)
2) Nivel de significancia: α= 0.05
3) Reemplazando los datos en la formula:
𝒁𝒄 =
𝒑− 𝝅
√𝝅(𝟏 − 𝝅)
𝒏
=
𝟎. 𝟕𝟗𝟒 − 𝟎. 𝟖𝟑𝟒𝟓
√𝟎. 𝟖𝟑𝟒𝟓(𝟏 − 𝟎. 𝟖𝟑𝟒𝟓)
𝟑𝟖𝟒
= −𝟐. 𝟏𝟑𝟔
4) Grafica y puntos críticos:
5) Interpretación: Con un nivel de significancia del 5% existe evidencia
estadística para rechazar la hipótesis nula. Se concluye que la proporción de
estudiantes que cuentan como máximo 350 horas de prácticas es menor a
0.8345.