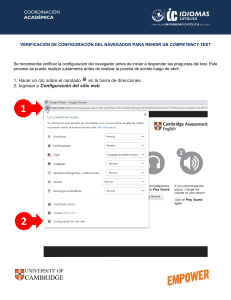
UNIVERSIDAD NACIONAL DE INGENIERÍA Ciclo Académico: 2021- III FACULTAD DE INGENIERÍA ELÉCTRICA Y ELECTRÓNICA Fecha: CURSO: Dispositivos y Circuitos Electrónicos I TIPO DE PRUEBA: PRACTICA No. 1 03-02-22 Duración: DEPARTAMENTOS ACADÉMICOS Ex. PARCIAL 1H. 50 m. COD. CURSO: EX. FINAL EE418M EX. SUST. Apellidos y Nombres:……………………………………………………………………….. Nota: Son tres problemas dura 110 minutos incluyendo la subida a Moolde pasado este tiempo no podrán entregar el problema (subir fotografía del celular legible o escaneado) Problema 1.- (6 Puntos) a) La energía de la banda prohibida del germanio puro es Eg = 0.67 eV. Calcular el número de electrones por unidad de volumen en la banda de conducción a 250. °K, 300 °K, y a 350 °K. (1PT.) b) Hacer lo mismo para el silicio suponiendo que Eg = 1.1 eV. La masa efectiva de los electrones y huecos son en el germanio es 0.12 me y 0.23 me, y en el silicio 0.31 me y 0.38 me, donde me = 9.1·1031 Kg es la masa de electrón libre. (1PT.) c) Supóngase que la masa efectiva de los huecos en un material es 4 veces la de los electrones. A que temperatura el nivel de Fermi estará un 10% por encima del punto medio de la banda prohibida. Sea Eg = 1 eV. (1PT.) d) A una barra de Ge de 12 cm de longitud y 2 cm 2 de sección se le aplica una tensión de 10 V entre sus extremos. Conociendo como datos la concentración intrínseca de portadores, ni = 2.36·1020m–3, que n (300K) = 0.39m2/Vs y que p (300K) = 0.182 m2/Vs, determinar: (1) la resistividad del Ge; (2) la resistencia de la barra; (3) la velocidad de arrastre de electrones y huecos; y (4) la corriente que circula por la barra. (3PT.) Problema 2.- (6 Puntos) a) En una muestra de Si tipo N, en equilibrio térmico y a 300K, se conoce la resistividad, ρ =6 Ω-m, n = 1600 cm2/Vs, p = 600 cm2/Vs, ni =1.4·1010cm-3 la densidad efectiva de estados en la BC, NC = 1019cm-3. Con estos datos, determinar: (1) la concentración de electrones y huecos a partir de las expresiones de la conductividad y de la ley de acción de masas; (2) la localización del nivel de Fermi a partir de la expresión: n = NC exp[(EF–EC)/(kT)]; (3) la probabilidad de que un estado del nivel donador esté ocupado y la probabilidad de que no lo esté, sabiendo que EC–ED = 0.05 eV. (4.5PT.) 2 b) Se desea dopar una barra de Si de longitud 30 mm y sección 5 mm de forma que al ser sometida a una tensión de 10 V sea circulada por una intensidad de 2mA. Calcúlese la concentración de donadores ND, con que debe doparse la barra. Nota: despréciese la concentración de huecos en el análisis y estímese el error cometido por este motivo en el valor de la resistencia de la barra. Datos: ni = 1.45·1016 m-3, n= 1500 cm2/Vs y p = 475 cm2/Vs. (1.5PT.) Problema 3.- (8 Puntos) Una barra de germanio tiene la forma indicada en figura, donde L= 0.5 cm. H=W= 0,1 cm. Si la barra es intrínseca siendo p= 2·1014 cm–3 a la temperatura de 300 °K y n=4400 cm2/v-s; p=2200 cm2/v-s a) Hallar la conductividad y la resistencia media entre los extremos de la barra. (2PT.) b) Si se sabe que la barra es de tipo n y que tiene una resistencia de 16 Ω ¿Cuál es la concentración de donantes? (2PT.) c) A que temperatura el voltímetro marca 4 voltios, cuando el material es intrínseco. (2PT.) d) ¿Cuál es la fracción de corriente que se transporta en los huecos para el caso (b)? (2PT.) H 12V 1k + 4V R L (Barra de germanio) - W El Profesor