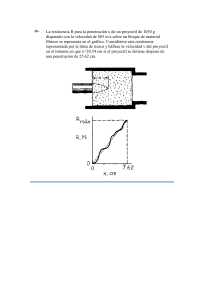
Instituto tecnológico superior de Coatzacoalcos. INGENIERÍA PETROLERA Asignatura: Dinámica Alumno: Dominguez Arias Hilario Grado y grupo: 3 “A” Actividad 1: Investigación Docente: Ing. Eladio Aquino Ordaz Unidad 1 Horario de clases Lunes 7:00-9:00 Miércoles 7:00-9:00 Viernes 7:00-9:00 Investigar 1-Movimiento Uniformemente Acelerado. 2-Moviento de proyectiles y sus ecuaciones. 3-Componentes transversales y Radiales de velocidad. En formato de Word. Con nombre completo. Numero de actividad y datos de asignatura. Subir en formato pdf. Movimiento Uniformemente Acelerado El movimiento rectilíneo uniformemente acelerado (m.r.u.a.) o movimiento rectilíneo uniformemente variado (m.r.u.v.) en tu día a día es bastante común. Por ejemplo, si dejas caer una moneda al suelo (caida libre), esta realizará un movimiento rectilíneo uniformemente acelerado (m.r.u.a.) o movimiento rectilíneo uniformemente variado (m.r.u.v.). En este apartado vamos a estudiar las ecuaciones y las gráficas que definen a este movimiento. Un cuerpo realiza un movimiento rectilíneo uniformemente acelerado (m.r.u.a.) o movimiento rectilíneo uniformemente variado (m.r.u.v.) cuando su trayectoria es una línea recta y su aceleración es constante. Esto implica que la velocidad aumenta o disminuye su módulo de manera uniforme. A la aceleración responsable de que cambie el módulo de la velocidad (también llamado celeridad o rapidez), se le denomina aceleración tangencial. Ecuaciones y Gráficas del M.R.U.A. Velocidad Su unidad en el Sistema Internacional (S.I.) es el metro por segundo (m/s). Cambia de manera uniforme y se obtiene por medio de la siguiente expresión: v=v0+a⋅t Dónde: v0 es la velocidad inicial. a es la aceleración que tiene el cuerpo. t es el intervalo de tiempo en el que se estudia el movimiento. A mayor pendiente, mayor es la aceleración del cuerpo. Posición Su unidad en el Sistema Internacional (S.I.) es el metro (m) y se calcula mediante la siguiente expresión: x=x0+v0t+12at2 Dónde: x0 es las posición inicial. v0 es la velocidad inicial. a es la aceleración. t es el intervalo de tiempo en el que se estudia el movimiento. Gráficamente se trata de una parábola donde x0 representa la posición inicial del cuerpo y a la aceleración del mismo. Aceleración Su unidad en el Sistema Internacional (S.I.) es el metro por segundo al cuadrado (m/s2). Su valor permanece constante y distinto de 0. a=cte Cuando: a>0, la velocidad aumenta su valor y se dice que el cuerpo está acelerando. a<0, la velocidad disminuye su valor y se dice que el cuerpo está frenando. Observa lo que t representa en las ecuaciones anteriores: El intervalo de tiempo durante el cual se mueve el cuerpo. Dicho intervalo a veces es representado por t y otras por ∆t. En cualquier caso t=∆t = tf - ti siendo tf y ti los instantes de tiempo inicial y final respectivamente. Por último, recuerda que, si consideras el eje vertical y, puedes encontrar la ecuación de posición anterior en la forma. y=y0+v0t+12at2. Movimiento de proyectiles y sus ecuaciones. Cualquier objeto que sea lanzado en el aire con una velocidad inicial de dirección arbitraria, se mueve describiendo una trayectoria curva en un plano. Para describir el movimiento es útil separarlo en sus componentes horizontal y vertical. 2. Entre las variables que constituyen el Movimiento de Proyectil son:I Rapidez inicial (tanto vertical como horizontal).J.Tiempo de subida.K.Tiempo de vuelo. Altura máxima. Alcance máximo horizontal. Posición en cualquier instante, tanto horizontal como vertical. 3. Rapidez horizontal inicial: se caracteriza, ya que es constante en toda la trayectoria del proyectil. Rapidez vertical inicial: 4. Tiempo de subida: es cuando el proyectil, alcanza la altura máxima y por lo tanto en ese instante, su velocidad vertical (vy) es cero. Al momento de alcanzar su altura máxima, vy = 0 5. Tiempo total de Vuelo: es el tiempo total de la trayectoria del proyectil; que es equivalente a dos veces al tiempo de subida (el tiempo que demora el proyectil en alcanzar la altura máxima, es el mismo tiempo que tarda en caer al suelo, en este caso, su punto de origen). 6. Alcance vertical máximo: es cuando el proyectil llega a obtener una velocidad vertical de cero; por lo tanto a partir de la ecuación de caída libre, podemos obtener la altura máxima del proyectil. Luego, procedemos a reemplazar la rapidez vertical inicial y el tiempo de subida; y nos queda. 7. Alcance Horizontal: es el recorrido horizontal total del proyectil. Posición vertical en cualquier instante: es la altura instantánea del proyectil en un instante dado. 8. Posición horizontal en cualquier instante: es el alcance horizontal del proyectil, en un instante dado. Componentes transversales y Radiales de velocidad Componente radial La velocidad radial es la forma más simple de velocidad. Es la velocidad y dirección de un objeto, en la línea recta, hacia o desde un observador, se utiliza comúnmente en ecuaciones cinemáticas básicas, determinando que tan rápido se mueve el objeto en un sistema y particularmente cuando se grafican y se dan coordenadas polares. Por ejemplo la determinación de la velocidad de un automóvil que se desplaza por la carretera recta resultara en un valor de velocidad radial de distancia sobre tiempo en una dirección particular. Componente transversal Debido a que no todos los objetos se mueven en línea recta, hay otros componentes de la velocidad a considerar. El término "tangencial" significa "tangente a" y el valor de la velocidad tangencial es la componente de este vector que se mueve perpendicularmente al movimiento radial. Este elemento de la velocidad entra en juego, así como la velocidad angular, para objetos que se mueven en un movimiento circular o de arco. También describe el movimiento de los objetos que están viajando en un triángulo y no directamente hacia o fuera del observador. Referencias Fisicalab.(27/09/2020).recuperado de https://www.fisicalab.com/apartado/mrua. Slideshare.(12,mayo,2010). Recuperado de https://es.slideshare.net/vicenteegalvez/ecuaciones-y-modelos-del-movimiento-deproyectiles#:~:text=%20Ecuaciones%20y%20Modelos%20del%20Movimiento%20 de%20Proyectiles,ya%20quees%20constante%20en%20toda%20la...%20More%2 0. Curso de dinámica. (27/09/2020). Recuperado de https://sites.google.com/site/cursodedinamicacom/componente-radial-ytransversal.