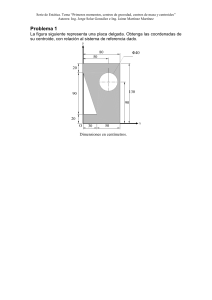
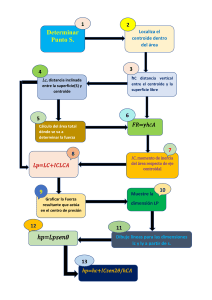
CURSO: “RIGGER” TRIANGULO DE SEGURIDAD EN IZAJE. Movimiento de cargas: Se refiere a todas las actividades de movimiento, transporte y elevación de cargas mediante el uso de grúas convencionales, de pluma, puentes rodantes y grúa, monorrieles, aparejos eléctricos, apiladoras, recuperadoras de minerales, pórticos, elevadores, camiones con hidrogrua, manipuladores de neumáticos todo terreno y cualquier tipo de accesorios de elevación. TIPOS DE CARGA ➢ Carga general: ▪ Carga con emb alaje . ▪ Carga suelt a ▪ Carga palet izad a ▪ Carga unita rizad a ▪ Carga preeslin gada ➢ Carga a granel: ▪ Sólida ▪ Líquida ▪ Gaseosa. ➢ Carga especial: • Carga pesada. • C a r g a r e f r i g e r a d a . • C a r g a p e l i g r o s a . • C a r g a v a l i o s a . . ➢ Carga contenida. Definiciones: Embalaje: Caja o cubierta con que se resguardan los objetos que han de transportarse. Empaque o recipiente con el que se facilita su manipulación, transporte y almacenaje. Estibar: distribuir convenientemente la carga en un vehículo. Pallets, paletas o tarimas: armazón de madera, plástico, metal u otros materiales empleado en el movimiento de carga ya que facilita el levantamiento y manejo con pequeñas grúas hidráulicas, llamados montacargas Ventajas al paletizar: • Facilita la manipulación de las mercancías. • Disminuye el tiempo de utilización de los muelles de carga • Reduce daños del producto durante el transporte • Permite utilizar mejor el espacio durante el transporte y almacenamiento de mercancías • Agiliza la carga y descarga de camiones CONTENEDORES.: Contenedores intermodales, contenedores ISO intermodales, contenedores de carga (conteiner: caja metálica o de fibra de vidrio de un mismo tamaño que permite movilizar mayor cantidad de carga en el menor tiempo posible. Se utilizan en el transporte marítimo o fluvial, transporte terrestre y transporte multimodal. Unidades que protegen las mercancías de la climatología y que están fabricadas de acuerdo con la normativa ISO (International Standarization Organization), en concreto, ISO-668. Características de contenedores: Elemento básico del intermodalismo. • Fabricados principalmente de acero corten, aluminio y algunos otros de madera contrachapada reforzados con fibra de vidrio. • El suelo es de madera, aunque ya hay algunos de bambú. • Interiormente llevan un recubrimiento especial anti-humedad, para evitar las humedades durante el viaje. • En cada una de sus esquinas, tienen una conexión (twistlocks), que les permiten ser enganchados por grúas especiales, así como su ensamblaje tanto en buques como en camiones. Dimensiones de los contenedores: • El ancho se fija en 8 pies • El alto varía entre 8 pies y 6 pulgadas o 9 pies y 6 pulgadas • El largo varía entre 8 pies, 10 pies, 20 pies, 40 pies, 45 pies, 48 pies y 53 pies. • Los más extendido a nivel mundial son los equipos de 20 y 40 pies, con un volumen interno aproximado de 32,6 m3 y 66,7 m3 respectivamente. • Las dimensiones de los contenedores están reguladas por la norma ISO 6346. • El peso límite máximo es de 20,000 kgs para los de 20 pies y de 25,000 kgs para los de 40. • TEU (Twenty-foot Equivalent Unit = Unidad Equivalente a Veinte Pies) representa una unidad de medida de capacidad inexacta del transporte marítimo (Buques portacontenedores y terminales portuarios para contenedores) expresada en contenedores. • Una TEU es la capacidad de carga de un contenedor normalizado de 20 pies que puede ser transferido fácilmente entre diferentes formas de transporte tales como buques, trenes y camiones. Existen otras variantes del contenedor que se calculan como equivalentes a 2 TEU o 1 FEU (Forty-foot Equivalent Unit). Tipos de contenedores: Seco (Dry van): Contendor básico, cerrado herméticamente, sin refrigeración ni ventilación. Metálicos: como los estándar, pero sin cerrar herméticamente y sin refrigeración. Empleados comúnmente para el transporte de residuos y basuras por carretera. High Cube: contenedores estándar mayoritariamente de 40 pies; su característica principal es su sobrealtura (9,6 pies). Refrigerado (Reefer): Contenedores refrigerados, ya sea de 40 o 20 pies, pero que cuentan con un sistema de conservación de frío o calor y termostato. Deben ir conectados en el buque y en la terminal, incluso en el camión si fuese posible o en un generador externo, funcionan bajo corriente trifásica. Abierto de arriba (Open Top): de las mismas medidas que los anteriores, pero abiertos por la parte de arriba. Puede sobresalir la mercancía pero, en ese caso, se pagan suplementos en función de cuánta carga haya dejado de cargarse por este exceso. Parrilla lisa (Flat rack): carecen también de paredes laterales e incluso, según casos, de paredes delanteras y posteriores. Se emplean para cargas atípicas y pagan suplementos de la misma manera que los open top. Abierto de un lado (Open Side): su mayor característica es que es abierto en uno de sus lados, sus medidas son de 20 o 40 pies. Se utiliza para cargas de mayores dimensiones en longitud que no se pueden cargar por la puerta del contenedor. Contenedor cisterna (Tank): para transportes de líquidos a granel. Se trata de una cisterna contenida dentro de una serie de vigas de acero cuyas dimensiones son equivalentes a las de un "dry van". La cisterna puede apilarse y viajar en cualquiera de los medios de transporte típicos del transporte intermodal. Cisterna (flexi tank): para transportes de líquidos a granel. Un flexi-tank consiste en un contenedor estándar (dry van), normalmente de 20 pies, en cuyo interior se fija un depósito flexible de polietileno de un solo uso denominado flexibag Plataforma: sólo tiene piso, carece de paredes. Cualquier carga es más segura de manipular, levantarla y ponerla en la superficie como si fuera un contenedor. Animales vivos: Contenedores para transportar animales con ventanas para que respiren y se alimenten. Granelero: en lugar de tener puertas tiene una perforación arriba y los productos se vierten dentro FORMAS Y SIMETRIAS. Los accesorios de elevación deberán seleccionarse en función de las cargas que se manipulen, de los puntos de prensión, del dispositivo del enganche y de las condiciones atmosféricas, y teniendo en cuenta la modalidad y la configuración del amarre.(EFECTOS DE FORMA) Ejemplos de cargas simétricas: Ejemplo de carga asimétrica: UNIDADES DE MEDICION • ¿QUÉ SON LOS PREFIJOS? Los prefijos son una forma abreviada de expresar cifras o números muy grandes apoyado en el conocimiento de las potencias, de tal modo, se asigna una letra en representación de una potencia de 10 especifica. Ejemplo: 3 1km= 1x10 m=1x1000 m= 1000 m 3 1kgr= 1x10 gr=1x1000 gr=1000 gr -6 1 µm= 1x 10 m= 1x 0,000001m Ejercicio: 1) 1 mm=? 2) 2ml=? 3) 6kPa=? 4) 8MPa=? 3 5) 6cm =? 2 6) 9 km =? 7) 3GB=? 8) 12 µm=? 9) 82cm=? 10) 28 hPa=? ¿QUÉ ES LA CONVERSIÓN DE UNIDADES? La conversión de unidades es la transformación del valor numérico de una magnitud física, expresado en una cierta unidad de medida, en otro valor numérico equivalente y expresado en otra unidad de medida de la misma naturaleza. Este proceso suele realizarse con el uso de los factores de conversión y las tablas de conversión de unidades. Frecuentemente basta multiplicar por una fracción (factor de una conversión) y el resultado es otra medida equivalente, en la que han cambiado las unidades. Cuando el cambio de unidades implica la transformación de varias unidades, se pueden utilizar varios factores de conversión uno tras otro, de forma que el resultado final será la medida equivalente en las unidades que buscamos, por ejemplo si queremos pasar 8 metros a yardas, lo primero que tenemos que hacer, es conocer cuánto vale una yarda en metros para poder transformarlo: una yarda (yd) = 0,914 m, luego dividir 8 entre 0,914 y nos daría como resultado 8,75 yardas. Ejemplo: 1m=100cm 1cm=10mm o bien se puede decir -3 1 mm= 1/10 cm=1/1000m=1x10 m PARA CONVERTIR Toneladas largas Toneladas largas Toneladas métricas Toneladas métricas Toneladas cortas Toneladas cortas A Toneladas cortas Toneladas métricas Toneladas largas Toneladas cortas Toneladas métricas Toneladas largas MULTIPLICAR POR: 1.12 1.016 0.9844 1.1025 0.9078 0.89287 TON= una tonelada corta (U.S.A.) =2000 libras Una tonelada larga (U.K.) = 2240 libras Una tonelada métrica (Mex) =2205 libras Existen 3 metodologías para convertir: Metodología 1.-regla de 3 simples 2 Ejemplo: Convertir 2 Acre a cm 2Acre→ X m2 1Acre→ 4046,856m2 X=2 Acre x 4046,856 m2 1 Acre X=8093,712 m2 8093,712 m2→ X cm2 X=8093,712 m2 x 10000 cm2 1 m2→10000 cm2 1 m2 X=80937120 cm2 Metodología 2.- regla del mapa vial. 2 2 2 Acre x 4046,856 m x 10000 cm =80937120 cm 2 1 Acre 1m 2 Metodología 3.- siguiendo regla de prefijos Ejercicios. 2 2 -4 2 2 Acre x 4046,856 m =8093,712 m ==80937120x10 m =80937120 cm 1 Acre Nota: -2 2 -4 c=10 … c = 10 Ejercicio: Convertir mediante los 3 métodos 1. Convertir 10 ft a cm 3 2. Convertir 20ft a cm 3 3. Convertir 10 Ton( métrica) a gr 4. Convertir 80ft a in 5. Convertir 10 in a m 3 6. Convertir 20m a lt 3 3 2 2 7. Convertir 20ft a cm 8. Convertir 20ft a cm 9. Convertir 2 milla a yarda. 10. Convertir 80 ton(corta) a ton (métrica). CONCEPTOS FÍSICOS APLICADOS MASA (m) ✓ Es la cantidad de materia de un cuerpo. 2 ➢ Unidades de medición en sistema internacional: Gramo [g] y sus prefijos, principalmente el Kilogramo [kg] ➢ Unidades de medición en sistema ingles: Libra [lb]; Tonelada [t] FUERZA: Magnitud física que mide la intensidad del intercambio de momento lineal entre dos partículas o sistemas de partículas (en lenguaje de la física de partículas se habla de interacción). Según una definición clásica, fuerza es todo agente capaz de modificar la cantidad de movimiento o la forma de los cuerpos materiales. No debe confundirse con los conceptos de esfuerzo o de energía. En el Sistema Internacional de Unidades, la fuerza se mide en Newton (N). PESO (P): Es la fuerza con la cual un cuerpo actúa sobre un punto de apoyo, originado por la aceleración de gravedad, cuando esta actúa sobre la masa del cuerpo. P=mxg donde, m = masa en [kg] y g = 9,81 [m/s2], P = 1 [kg] x 9,81 (m/s2) = 9,81 [kg m/s2] = 9,81 [N] = 1 [kp] 1 [N] = 1 [kg] x 1 [m/s2] FUERZA DE GRAVEDAD (Fg): Es una fuerza de atracción entre todo tipo de materia, y es muy débil con respecto a las otras fuerzas de la naturaleza. La fuerza gravitacional entre dos objetos depende de sus masas, que es la razón por la cual solamente podemos ver a la gravedad en acción cuando al menos uno de los objetos es muy grande, como la tierra. Aceleración de gravedad (g): La gravedad es una de las cuatro interacciones fundamentales. Origina la aceleración que experimenta un cuerpo físico en las cercanías de un objeto astronómico. También se denomina interacción gravitatoria o gravitación. Por efecto de la gravedad tenemos la sensación de peso. Si estamos situados en las proximidades de un planeta, experimentamos una aceleración dirigida hacia la zona central de dicho planeta —si no estamos sometidos al efecto de otras fuerzas—. En la 2 superficie de la Tierra, la aceleración originada por la gravedad es 9.81 m/s , aproximadamente. PESO ESPECÍFICO Cociente entre el peso de un cuerpo y su volumen. Para calcularlo se divide el peso del cuerpo o porción de materia entre el volumen que éste ocupa. Nota: Pare ello debemos tener a mano los datos de peso específico o densidades que se sacan de tablas y hay estar muy claro en lo que es el cálculo de área y volumen de un cuerpo. Ejercicios: 1. La pieza esta compuesta de dos barras homogeneas.La barra 1 es de una 3, aleacion de tungteno con densidad 14000 kg/m mientras que la barra 2 es de acero con densidad 7800 kg/m3.Dtermine el peso de cada barra y el peso total del cuerpo compuesta por estas dos barras. 2. Ahora repita el mismo ejercicio anterior pero con los datos entregado en tabla. 3. El cuerpo compuesto consiste en una barra soldada a un cilindro. La barra 3 homogénea es de aluminio (peso específico 168 lb/ft ), y el cilindro 3 homogéneo es de bronce (peso específico 168 lb/ft ). Determine el peso total del cuerpo. 4. Repetir el ejercicio anterior con los datos de peso específico sacados de tabla 5. Determine el peso del bloque de cemento de la siguiente figura. 6. Determine el peso del pieza de acero de la siguiente figura. 7. Determine el peso del cuerpo de madera de la siguiente figura. 8. Determine el peso del componente de acero de la siguiente figura. µ 9. Determine el peso de la pieza de bronce de la siguiente figura 10. Determine el peso de la pieza de acero de la siguiente figura CENTROIDE Y CENTROS DE MASA El peso de un cuerpo no actúa en un solo punto sino que esta distribuido sobre un volumen total. Sin embargo, el peso se puede representar con una sola fuerza equivalente actuando en un punto llamado centro de masa. Por ejemplo, cada pate de un automóvil tiene un peso, pero podemos representar su peso total con una sola fuerza que actúa en su centro de masa. También, las posiciones medias de un cuerpo, se llaman centroide, por lo que se define, que pueden interpretarse como las posiciones medias de áreas, volúmenes y líneas. Los centroides coinciden con los centros de masa en clases particulares de cuerpos, pero también surgen en muchas otras aplicaciones. ` CENTROIDE. Como el centroide tiene tantas aplicaciones, lo definimos primero usando el concepto general de un “peso ponderado”. Por lo tanto, se debe analizar los centroides de línea, área y volumen. Antes que el centroide o centro de masa. (a) Grupo de estudiantes en un aula. El concepto básico con el que podemos comenzar es de una posición media. Supongamos que queremos determinar la posición media de un grupo de estudiantes en un aula. Primero establecemos un sistema coordenado para poder expresar la posición de cada estudiante. Por ejemplo, alinear los ejes con las paredes (figura a). Numeramos los estudiantes del 1 hasta N y anotamos la posición del estudiante uno como x1,y1;etc.La coordenada x media es la suma de sus coordenadas divida entre N, b) Posición media. Supongamos ahora que repartimos entre los estudiantes cierto número de monedas (Por ejemplo, c1 es el número de monedas entregadas al estudiante un 1). ¿Cuál es la posición media de los estudiantes? Está claro que la que no puede ser igual que la posición media de los estudiantes repartidos por la sala. Por ejemplo, si los estudiantes ubicados al frente del aula tienen más monedas, la posición media de las monedas estará más cerca del frente del aula que la posición media de los estudiantes. Lo que nos da como coordenadas finales del centroide o punto medio de distribución las monedas Para determinar las coordenadas x de la posición media de las monedas, necesitaremos sumar las coordenadas x de las monedas divididas entre el número total de monedas repartidas. Podemos obtener la suma de las coordenadas x de las monedas multiplicando el número de monedas que cada estudiante recibió por la coordenada x donde se encuentra ubicado el estudiante y sumar los productos parciales. Osea, la fórmula general para centroide es: Asignando otros significados a c1, c2, c3,….cn, podemos determinarlas posiciones medias de otras medidas asociadas con el ejemplo de los estudiantes, lo que a su vez se puede extrapolar en otros ejemplos y aplicaciones. Por ejemplo, determina la posición media de sus edades, peso o estaturas. Por lo tanto, las ecuaciones antes descritas, sirven para determinar posición media de cualquier conjunto de cantidades alas que podemos asociar posiciones. Una posición media obtenida de esas ecuaciones se denomina, “posición de peso ponderado”, CENTROIDE. El “peso” asociado con las posiciones (x1,y1), es c1 y el peso asociado con la posición (x2,y2), es c2 ,etc, por lo que si “p” es igual al peso la ecuación también se puede expresar como: Cálculo de Centroide . Método de Elementos compuestos: Un área, un volumen o una línea compuesta es una combinación de partes simples. Por lo que es más fácil, determinar el centroide, si se conocen los centroides de las partes más simples conocidas. Ejemplos Areas: (a) Área compuesta de El área compuesta de la figura (a), consiste en un triángulo, un rectángulo y un semicírculo, que llamaremos parte 1, 2 y 3, por lo tanto, la coordenada X y en Y del centroide del área será: tres áreas simples Cuando un área se puede dividir en partes cuyos centroides son conocidos ( tabla), podemos usar esas expresiones para determinar su centroide. Esto es, iniciando el análisis de la figura que se desea calcular el centroide, dividiéndola en partes finitas y planteando las ecuaciones necesarias similarmente a lo descrito en posición de peso ponderado. (a) Area recorte con un (b)Área triangular y area del recorte Los resultados , son aproximados por la incertidumbre en las posiciones de las partes del area. Las ecuaciones en si son identicas, excepto que las posiciones de las partes son sus centroides. El área de la figura consiste en un área triangular con un “agujero “circular. Designando el área triangular ( sin agujero) como parte 1 del área compuesta y el área del agujero como parte 2, obtenemos la coordenada x del centroide del área compuesta Esta ecuación se comporta idénticamente a las primeras ecuaciones, excepto que los términos correspondientes al agujero son negativos. Volúmenes y líneas Los centroides de volumen y líneas compuestos se pueden obtener usando el mismo método que para las áreas. Por lo tanto… Volumen Líneas Centro de masa ( CM). Las coordenadas del centro de masa de un cuerpo compuesto de partes con masa m1, m2,…son Donde , , son las coordenadas de los centros de masa. Y si el peso es W= m*g , esto también se puede expresar multiplicando a las coordenadas del centro de masa por la aceleración de gravedad “g”, quedando la expresión. Procedimiento de trabajo: Los pasos para definir un centroide de área, volumen o centro de masa son 3: 1. Escoger las partes, trate de dividir el elemento en partes cuyo centroides se conozcan o se puedan determinar con facilidad. 2. Determine los valores para las partes. Determinando el centroide y el área, el volumen o masa de cada parte. Vea si hay relaciones de simetría que puedan simplificar la tarea. 3. Calcular el centroide. Use las ecuaciones para determinar el centroide del elemento compuesto. Ejemplo: 1.-Determine el centroide del área de la figura. Donde b = 3m, c= 2m y R= 3.5 m SOLUCION: PASO 1.- Selección de las partes: Podemos dividir en tres partes el área total, un triángulo, un rectángulo y un semicírculo. Que llamaremos a sus respectivas áreas A1, A2, A3. (a) Coordenadas en eje X (b)Coordenadas en eje Y de los de los centroides de las centroides partes. PASO 2.- Determinacion de los valores de las partes. Enla figura (a) y (b), se muestran las coordenadas en el eje x del centroide del area de cada figura o Area encontrada. ( m) (m) A (m2) Figura N° 1 Triangulo =2.3 Figura N° 2 Rectángulo R=3.5 Figura N° 1 Semicírculo R=3.5 PASO 3.- Cálcular el Centroide. Se procede a calcular el centroide del eje x, según se indica a continuacion: Luego, procede calcular el centroide del eje y, según se indica a continuación: 2.-Determine el centroide del área de la siguiente figura. SOLUCION: PASO 1.- Selección de las partes: Podemos dividir en 2 partes el área total, un, un rectángulo y un semicírculo. Que llamaremos a sus respectivas áreas A1, A2. Por lo tanto, trataremos el área como un área compuesta, que consiste en un área rectangular completa (sin recorte) y el área de recorte sobre el rectángulo que será semicircular. A1 Área de Rectángulo y A2 Área de recorte semicircular. PASO 2.- Determinacion de los valores de las partes. Enla figura (a) y (b), se muestran las coordenadas en el eje x del centroide del area de cada figura o Area encontrada. ( mm) (mm) A (mm2) Figura N° 1 Rectángulo Figura N° 2 R=100 Semicirculo PASO 3.- Cálcular el Centroide. Se procede a calcular el centroide del eje x, según se indica a continuacion: Luego, procede calcular el centroide del eje y, según se indica a continuación: 3.-Determine el centroide del volumen de la siguiente figura. h=4 cm b=4 cm R=2 cm SOLUCION: PASO 1.- Selección de las partes: Podemos dividir en tres partes el volumen total, centroide del cono y el cilindro. Que llamaremos a sus respectivas áreas V1, V2. (a) Coordenadas del eje x del centroide del cono y el cilindro. PASO 2.- Determinacion de los valores de las partes. Enla figura (a) , se muestran las coordenadas en el eje x del centroide del area de cada figura o Area encontrada. Dado la posicionde referencia del eje cartesiano, se destaca el valor en el putnto medio en y ( cm) (cm) (cm) V (cm3) Figura Cono N° 1 0 0 Figura N° Cilindro 2 0 0 PASO 3.- Cálcular el Centroide. Se procede a calcular el centroide del eje x, según se indica a continuacion: Luego, procede calcular el centroide del eje Z e Y, pero debido ala simetría su valor es 0 en cada eje, según se indica a continuación,: 4.- Determine el centroide del volumen de la siguiente figura. ¿MASA = PESO?... . No , masa es cantidad de materia y peso es el nombre de la fuerza con la que un cuerpo es atraído hacia es centro de la tierra. Es decir, es un tipo de Fuerza. Cilindro grande R=25mm h=40mm Cilindro pequeño ( recorte) D=20mm r=10mm esp (espesor)= 20mm prisma L= 200 mm SOLUCION: PASO 1.- Selección de las partes: Podemos dividir en 5 partes el volumen total, centroide de 2 cilindros, 2 semicírculos y un prisma o barra rectangular con un recorte de un semicírculo más pequeño representado por la figura 5. Que llamaremos a sus respectivos volúmenes V1, V2, V3, V4, V5. (a) Division de volumenes en 5 partes (b) Posiciones de los centroides de las partes 1 y 3 62 PASO 2.- Determinacion de los valores de las partes. Enla figura (a) y (b) , se muestran las coordenadas en el eje x del centroide del area de cada figura o Area encontrada. Dado la posicionde referencia del eje cartesiano, se destaca el valor en el putnto medio en ( mm) (mm) (mm) V (mm3) Figura N° 1 Semicírculo 0 0 Figura N° 2 prisma rectangular recortado 0 0 Figura N° 3 Semicírculoo 0 0 Figura N° 4 Cilindro Figura N° 5 Cilindro 0 0 0 0 PASO 3.- Cálcular el Centroide. Se procede a calcular el centroide del eje x, según se indica a continuacion: Luego, procede calcular el centroide del eje Z e Y: Debido a la simetría su valor es 0 en cada eje, según se indica a continuación,: 62 5.- La pieza está compuesta de 2 barras homogéneas. La barra 1 es de una aleación 3 de tungsteno con densidad 14000kg/m , mientras que la barra 2 es de acero con 3 densidad 7800 kg/m . Determine el centro de Masa. SOLUCION: PASO 1.- Selección de las partes: Podemos dividir en dos partes la masa total de la barra en L, compuesta por 2 barras de distinto material la barra, 1 de tungsteno y la barra 2 de acero, que para efectos del cálculo de centro de masa llamaremos a sus respectivas masas m1, m2. 62 PASO 2.- Determinacion de los valores de las partes. En qla figura, se muestran las coordenadas en el eje x del centroide del area de cada figura o Area encontrada. Dado la posicionde referencia del eje cartesiano, se destaca el valor en el putnto medio en ( m) (m) (m) V (m3) m (kg) Figura N° 1 barra 0.04 0.12 0.02 de tungsteno 14000 10.752 Figura N° 2 barra 0.2 0.04 0.02 de acero 7800 5.9904 PASO 3.- Cálcular el Centroide. Se procede a calcular el centroide de masadel eje x, según se indica a continuacion: 62 Luego, se procede calcular el centroide del eje Z e Y,: 62 6.- En la figura, l cuerpo compuesto, consiste en una barra soldada a un cilindro. La barra es homogenia es de alumion (=168 )y el cilindro homogeneo es de bronce (= 530 ). Dertmine el centro de masa del cuerpo. Solución: Podemos determinar el peso de cada una de las partes homogéneas, multiplicando su volumen por su peso específico. Sabemos también, que el centroi de del cilindro se localiza en su centro, pero debemos determinar la localización del centroide de la barra, tratándola cómo un volumen compuesto ( se sugiere apoyo de tabla de datos como en ejemplos anteriores). Por lo tanto, el volumen del cilindro es Entonces ,… Y La coordenada de . El volumen de la barra es Podemos determinar el centroide de la barra tratando ésta como un volumen compuesto que consta de 3 partes. La parte 3 es un “recorte” semicircular y la parte 1 es el segmento semicircular del extremo dela barra. La parte 2corresponde al rectangular de la barra. a) División de la barra en 3 partes 62 b) Centroides de las 2 partes semicirculares En el caso del cálculo del centroide de la barra, la tabla quedaría de la siguiente forma: Parte N° 1 ( in) ( in) ( in) V ( in3) -1.7 0 0 Semicirculo N° 2 rectangulo N° 3 Recorte semicircular 5 0 0 8.3 0 0 -50.3 Donde en las coordenadas del eje x, el centroide presenta valores significativos, no siendo así, en el z e y, ya que debido ala simetría el valor medio es 0. Entonces, el centroide de volumen de la barra es: Y por lo tanto, el centroide de masa ( centro de masa) o centroide de peso completo de la figura es 0 en z e y , pero en x es: Ejercicios. Determine el centroide de las áreas de las siguientes figuras: 2.- 1.- 4.- 3.5.- 7.- 6.- 8.- 9.A.-Se tienen las dimensiones b=40 mm y h =20 mm. Determine la coordenada “Y” del centroide del área mostrada. B.-Si la sección transversal de la viga es A=0,01m2y la coordenada “Y” del centroide del área . ¿Qué valor tiene la dimensión b y h? Determine el centroide de volumen de las siguientes figuras: 11.- 10.Los agujeros tienen 3 in diámetro. 12.- 13.- 14.- 15.- 3 16.- El cilindro circular mostrado está hecho Aluminio ( Al) de 2700 kg/m y Hierro (Fe) 3 con densidad de 7860 kg/ m . a) Determine el centroide del volumen del cilindro. b) Determine el centro de masa del cilindro. 3 17.- El cilindro circular mostrado está hecho Aluminio ( Al) de 2700 kg/m . El tapon del 3 cilindro está hecho de Hierro (Fe) con densidad de 7800 kg/ m . Determine el centro de masa del cuerpo compuesto. 18.-Una maquina cnsta de 3 partes. Las mass y las posiciones de los centros de las masas son: Parte. Masa kg 1 2.0 100 50 -20 2 4.5 150 70 0 3 2.5 180 30 0 Determina las coordenadas del centro de masa de la máquina. 19.- Con el motor retirado, la masa del automovil es de 110 kg y su centro de masa esta en el punto C, como se muestra en la figura. La masa del motor es de 220 kg. Se requiere situar el centro de masa E del motor de manera que el centro de masa del automovil quede ala mitad de la distancia entre ruedas frontales A y las traseras B. ¿Qué valor debe tener b?. CENTRO DE GRAVEDAD El centro de gravedad es el punto de aplicación de la resultante de todas las fuerzas de gravedad que actúan sobre las distintas porciones materiales de un cuerpo, de tal forma que el momento respecto a cualquier punto de esta resultante aplicada en el centro de gravedad es el mismo que el producido por los pesos de todas las masas materiales que constituyen dicho cuerpo. En otras palabras, el centro de gravedad de un cuerpo es el punto respecto al cual las fuerzas que la gravedad ejerce sobre los diferentes puntos materiales que constituyen el cuerpo producen un momento resultante nulo. Paso 1: Considerar una figura 2D arbitraria. Paso 2: Suspéndase la figura desde un punto cercano a una arista. Marcar con línea vertical con una plomada. Paso 3: Suspéndase la figura de otro punto no demasiado cercano al primero. Marcar otra línea vertical con la plomada. La intersección de las dos líneas es el centro de masa. El centro de gravedad. De un cuerpo no corresponde necesariamente a un punto material del cuerpo. Así, el centro de gravedad de una esfera hueca está situado en el centro de la esfera que, obviamente, no pertenece al cuerpo. Factor de Angulo ( FA) El factor de Angulo es la relación entre la longitud de la eslinga medida desde el asiento del gancho hasta la parte superior de la carga y la altura vertical medida desde el asiento del gancho hasta la parte superior de la carga. Por lo tanto: Si observamos la figura, se puede afirmar que el factor de ángulo ( FA) será la relación de dividir L entre H: Lo que se deduce en consecuencia es, contamos con una relación constante directa para cada ángulo, lo que nos ayuda a determinar la tensión exacta que soporta cada eslinga, cuando se realiza una conexión angulada. Por lo tanto FA , también , equivale al porcentaje de capacidad de levante que tiene cada eslinga, la que va disminuyendo conforme el ángulo tiende a 0º y conforme tiende 90º la capacidad aumenta hasta un 100%. Es decir, mientras mas pequeño el ángulo, menor será la capacidad limite de trabajo( WLL) Calculo de Tensiones. La tensión o carga de trabajo de una eslinga, es la fuerza interna aplicada, que actúa por unidad de superficie o área sobre la que se aplica. También se llama tensión, al efecto de aplicar una fuerza sobre una forma alargada aumentando su elongación y está restringida por la carga máxima que soporta una determinada eslinga, valor que debe figurar visiblemente. Una situación común con un patrón de acentuación simple es cuando una varilla recta, con material uniforme y la sección transversal, se somete a tensión por las fuerzas opuestas de magnitud a lo largo de su eje. Si el sistema está en equilibrio y no cambiar con el tiempo, y el peso de la barra puede ser despreciada, a continuación, a través de cada sección transversal de la barra de la parte superior debe tirar de la parte inferior con la misma fuerza F . Por lo tanto el estrés a lo largo de la barra, a través de cualquier horizontal superficie, puede ser descrita por el número = F / A , donde A es el área de la sección transversal. Por otro lado, si uno se imagina la barra se corta a lo largo de su longitud, paralelo al eje, no habrá fuerza (por lo tanto sin estrés) entre las dos mitades de todo el corte. Los ángulos que se forman entre eslingas y la carga, son la clave para determinar la tensión (o WLL) para cada configuración. En las etiquetas de capacidad de las eslingas, se dan los WLL o tensiones máxima permitida (carga máxima) para las configuraciones en vertical, o en ángulo de 60, 45 y 30 º. Pero medir exactamente estos ángulos en terreno es muy difícil, o la mayoría de las veces no se tienen disponibles las herramientas apropiadas para esta labor. Sin embargo, dos ángulos que son fáciles de determinar antes de consultar tablas son: El primero es el ángulo de 90º, el cual se forma por dos eslingas de un ramal o por el aparejamiento en canasta en el gancho o eslabón maestro. Este ángulo en el accesorio (grillete, gancho o eslabón) corresponde a un ángulo de la eslinga de 45ª El segundo ángulo de fácil identificación, es el de 60º. Para un aparejamiento a 60º, el ángulo de la eslinga se puede reconocer, cuando la distancia entre los puntos de amarre es igual a la longitud de las eslingas. Finalmente, para calcular la tensión una eslinga queda circunscrito a: Donde P es el peso Ejemplo: Determine la tensión en las eslingas que levantan una columna de mármol, si el largo de cada eslinga es 10 m, según se indica en la figura Solución Tabla de datos. Largo de elingas N°1 yN° 2 es igual. L1=L2=10 m Masas es m=5000 kg Los ángulos que forman las eslingas en el punto de amarre con la cargas, sólo se conocen el de la eslinga N°1 No se conoce el ángulo de la eslinga N°2 No se conocen los factores de ángulos (Fa) Fa1=? y Fa2=? NO se conoce distancia entre puntos de amarre. D1=? y D2=? El Principal objetivo es determinar las tensiones T1=?? y T2=?? Formulas. Remplazando y calculando Basasndose en la funcion trigonometrica “seno”, se determina la altura del gancho hasta la carga Y basandose en la ec de pitagoras se encuentra la distancia D1 que es la distancia del punto de amarre al punto donde cae el gancho o centro de masa Como los Angulo son iguales Fa1= Fa2 ( admisible) Entonces basándonos en la formulas planteadas las tensiones son: Calcular el largo de eslinga y tensión de la eslinga posicionada en 30° en una maniobra de las siguientes características: Solución Tabla de datos. Largo de eslingas N°1 y N° 2 es igual. L1=L2= ¿? Masas es m=7500 kg Los ángulos que forman las eslingas en el punto de amarre con la cargas, sólo se conocen el de la eslinga N°1 No se conoce el ángulo de la eslinga N°2 No se conocen los factores de ángulos (Fa) Fa1=? y Fa2=? No se conoce distancia entre puntos de amarre.que entes caso por la simetría de la carga D1= D2=? El Principal objetivo es determinar las tensiones T1=?? y T2=?? Formulas. Remplazando y calculando Y basandose en la ec de pitagoras se encuentra la distancia D1 que es la distancia del punto de amarre al punto donde cae el gancho o centro de masa =D2 Basasndose en la funcion trigonometrica “seno”, se determina la altura del gancho hasta la carga =L2 Basasndose en la funcion trigonometrica “seno”, se determina la altura del gancho hasta la carga Como los Angulo son iguales Fa1= ( admisible en el límite) Fa2 Entonces basándonos en la formulas planteadas las tensiones son: Ejercicios 1.-Determine la tensiónen las eslingassi el largo de cada eslinga es 8 m. 2.-Determine la tensión en las eslingas 3.- Determine la tensión de las eslingas si la viga es un “cuartón” de madera (5 x 5)cm. 4.- Determine la tensión de las eslingas y si los ángulos son admisibles para una buena maniobra. 4.- Determine la tensión de la eslinga y si los ángulos son admisibles para una buena maniobra. 3 Multiplicar por 1000 y queda en kg/m Fórmulas de área y volumen de cuerpos geométricos Figura Cilindro Esfera Cono Esquema Área Volumen Cubo A = 6 a2 V = a3 Prisma A = (perim. base •h) + 2 • area base V = área base h Pirámide Poliedros regulares Figura Esquema Nº de caras Área Tetraedro 4 caras, triángulos equiláteros Octaedro 8 caras, triángulos equiláteros Cubo 6 caras, cuadrados A = 6 a2 Dodecaedro 12 caras, pentágonos regulares A = 30 · a · ap. Icosaedro 20 caras, triángulos equiláteros 62 62