
El preseníe, manual que EUDEBA éfrece% i público de tiue^fQ ^dióm a
íes )^ x in clásico d é l a ciencia, á p e s ^ de^jm odeflípíflad. La fartiá de^^U
a u t^ l e x i í ^ de m ayores cómeptariás^ pero basta recordar q u e '^ n ric b
Eerkii (1901-195^fué^ünQ íf^lp§ fo r^ d o rés del muñólo contémpqjráneb.
Por sus aportes singüilires —_eri particular,^ los felatiyós al i^euÉrqns-
prime^
bia.
ha señalado 'SU claridall y^*método, asi como ío efemental ctt^su
desarrollo. No requierfe cono<a|mientos aVaiwados dS Írai,atémá4:icas,^un. que suponga que-el lector e f e fem iliariza^o con í&s principios· íu^da.;im eíia|es de la tefj^oraetría y j^ o r in ie tr ía ^ ' ·
'í >
^ ' t
i’ En c a ^ u l o s b r e ^ s ,’cóm plerneritádos'por 25 problairias para el estu' diante y ^ ^ 1rilusJ^aq|^!n£s. Fefcíni; Expone los siguientes temas: ÍJ Lo&4¡^tém asJ^j?^odinámicos;'lX) L* prirnéra í e y ^ e la term odm ám icá;'!!/) ^ a
% ségund^;lly de la term odinám ica; IV) La e n tro p ía; y fl^ptcnciáies^^r■ v 9 io 3 i^ m i'^ s; VI) Reateeio^nei en- j^stemas' gáséosps;; yíL).' L^ (rertnbdmámica.de las soluciones' diluidas' y VIH) L a constante' de e i^ b p ía .
. ·'
.
· . ’■ · 1'
¿i? ■ ‘
s
V
S ·'
V ...
N
• \ \ ’\
\ A'. \ V \
^ y w
v v x
7\
} \/'.i/
χ ϊ \ \!^t \ i/ ^V ΗV μ wΦ - ^y /ί ' /· Φ Ί ^ '
( V \/'V
,
/i A j·■
■
-, /
/1'■*''A
'
Ji :^ f\\ ,
1 \ .i· ■ k
; 1. i '
i^'i' -'-'Ί
il· J 'î
/. /
/■
0 P
/ ■A Ä
1? A n i, I ’ h
^ /y fe Z /v v y w y ^ ^ ^
/:
' ·./>
v\ /\ :A y\ jiv
i
.H ^ A ïÎÎj5 ^ ··-
V V \ W
m
■■
.
Fermi, Enrico
Termodinámica / Enrico Fermi; traducido por Esther Rosen­
blatt. 5a. ed. Buenos Aires: EUDEBA, 1 9 8 5
X, 150 p., 22,5 cm. (Manuales)
Bibliografía; p. 145.
ISBN 950-23-0100-5
O
Inst. Bib. - UBA
M A N U A L E S / FÍSIC A
TERMODINÁMICA
ENRICO FERMI
EDITORIAL UNIVERSITARIA DE BUENOS AIRES
Título original de la obra en inglés:
Thermodynamics
Traducida por
Esther Rosenblatt
Quinta edición; enero de 1985
EUDEBA S.E.M.
F u n d a d a p o r la Universidad de B u e n o s Aires
© 1985
EDITORIAL U N IVERSITARIA D E BUENO S AIRES
Sociedad de E c on o m ía M ixta
Rivadavia 1571/73
Hecho el depósito que marca la ley 11.723
;SBN 950-23-0100-5
IMPRESO EN LA ARGENTINA
ÍNDICE GENERAL
Prefacio
........................................................................ .................................................
Introducción
IX
.................................
XI
I. LOS SISTEMAS TERMODINAMICOS ...................... ......................................
1. El estado de un sistem a y su s t r a n s fo r m a c io n e s ..........................
2. G ases ideales o perfectos ..........................................................................
1
1
8
II. LA PRIMERA LEY DE LA TERMODINÁMICA ....................................
3. Formulación de la primera ley de la term odinám ica ............
4. Aplicación d e la primera ley a sistem as cuyos estados pueden
representarse en un diagram a (V ,p) ..................................................
5. Aplicación de la primera le y a los gases .........................................
6. Transform aciones adiabáticas de un gas .........................................
11
11
18
20
24
SEGUNDA LEY DE LA TERMODINAMICA ..................................
Formulación de la segunda ley de la term odinám ica .................
El ciclo de Carnot ......................................................................................
La tem peratura term odinám ica absoluta .........................................
M áquinas térm icas .........................................................................................
28
28
30
33
41
ENTROPIA ............................................................................ ............................
A lgunas propiedades de los c i c l o s .........................................................
La entropía ................................................ .................. ...................................
O tras propiedades de la e n t r o p í a ...........................................................
La entropía de sistem as c u y o s estados pueden ser representa­
dos en un diagram a (V ,p) ................. ......................................................
15. La ecuación de Clapeyron ................. ....................................................
16. La ecuación de va n der W a a l s .................. .............................................
43
43
45
51
III. LA
7.
8.
9.
10.
...........................................................................
IV. LA
11.
12.
13.
14.
55
59
65
V. POTENCTALES TERMODINAMICOS .................................................................... 72
17. La energía libre .............................................................................................
72
18. El potencial term odinàm ico a presión constan te .........................
77
19. La regla de las f a s e s ...................................................................................
80
20. Termodinámica de la celda electrolítica reversible ...................
87
VI. REACCIONES EN SISTEMAS G A S E O S O S ....................................................
21. Equilibrio quím ico en lo s g a s e s ..............................................................
22. La caja de reacción de v a n ’t H off .......................................................
23. Otra dem ostración de la ecuación de equilibrio de sistem as
g a s e o s o s ............................................................ ....................................................
24. D iscusión del equilibrio de sistem as gaseosos. El principio de
Le Chatelier .......................................................................................................
91
91
93
99
101
V
VII. TERMODINAMICA DE LAS SOLUCIONES DILUIDAS ......................... ................... 105
25. Soluciones diluidas .........................................................................................
105
26. Presión osm ótica .............................................................................................. 110
27. Equilibrio quím ico de las soluciones ..................................................
115
28. La distribución de un so lu to entre dos f a s e s .................................
118
29. La presión de vapor, el p u n to de ebu llición y el punto de con­
gelación de una s o l u c i ó n ............................................................................. 121
Vm.
CONSTANTE DE E N T R O P ÍA ................................................ .............
El teorema de N e m st ................................................................................
El teorem a d e N e m s t aplicado a só lid o s ......................................
La constan te de entropía d e lo s g a se s ...........................................
Ionización térm ica d e u n gas: efecto term oiònico ............
129
129
132
136
140
BIBLIO G R AFIA.....................................................................................................................
145
ALFABÉTICO ........................................................................ ..............................
147
i ñ
LA
30.
31.
32.
33.
ín d ic e
VI
PREFACIO
Este libro tuvo su origen en un curso desarrollado durante el
verano de 1936 en la Universidad de Columbia, en Nueva York.
Es un tratado elemental dedicado exclusivamente a la termo­
dinámica pura. Se supone, sin embargo, que el lector está fami­
liarizado con los elementos fundamentales de la termometria y ca­
lorimetría. De tanto en tanto se hallarán breves referencias a la
interpretación estadística de la termodinámica.
Como guía para la elaboración de este libro, el autor se ha
valido de las notas tomadas durante el curso por el doctor Lloyd
Motz, de la Universidad de Columbia, quien asimismo se ocupó de
revisar el manuscrito. Agradezco aquí su generosa e inteligente
colaboración.
E. Fermi
INTRODUCCIÓN
La termodinámica trata fundamentalmente de las transfor­
maciones del calor en trabajo mecánico y de las transformaciones
opuestas del trabajo mecánico en calor.
Hace rektivamente poco tiempo que los físicos llegaron a la
conclusión de que el calor es una forma de energía que puede ser
transformada en otras formas de energía. Anteriormente, los cien­
tíficos pensaron que el calor era una especie de fluido cuya can­
tidad total era invariable; interpretaban el calentamiento de un
cuerpo y otros procesos análogos como consistentes simplemente
en la transferencia de este fluido de un cuerpo a otro. Es por lo
tanto digno de tenerse en cuenta que Carnot pudo, en el año
1824, basado en esta teoría del fluido calórico, llegar a un conoci­
miento relativamente claro de las limitaciones existentes en el
proceso de transformación del calor en trabajo, es decir, a la for­
mulación de lo que ahora se conoce como la segunda ley de la
termodinámica (ver. cap. III).
En 1842, apenas dieciocho años después, R. J. Mayer descubrió
la equivalencia entré el calor y el trabajo mecánico y formuló por
primera vez el principio de conservación de la energía (primera ley
de la termodinámica).
Sabemos actualmente que la base real para la equivalencia
entre el calor y la energía dinámica debe buscarse en la interpre­
tación cinética, que reduce todos los fenómenos térmicos a los
movimientos desordenados de átomos y moléculas. Desde este
pimto de vista, el estudio del calor debe considerarse como una
rama particular de la mecánica: la mecánica de un conjunto tan
enorme de partículas (átomos o moléculas) que la descripción de­
tallada del estado y el movimiento pierde importancia y solo de­
ben considerarse las propiedades en promedio de un gran número
de ellas. Esta rama de la mecánica, conocida como rnecánica esta­
dística, que se ha desarrollado fundamentalmente a través de los
trabajos de Maxwell, Boitzmann y Gibbs, ha conducido a una ade­
cuada comprensión de las leyes fundamentales de la termodiná­
mica.
TX
El enfoque de la termodinámica pura es diferente. Las leyes
fundameni;ales se toman aquí como postulados basados en la evi­
dencia experimental, y a partir de ellos se extraen conclusiones,
sin adentrarse en el mecanismo cinético de los fenómenos. Este
procedimiento tiene la ventaja de ser independiente, en gran me­
dida, de las hipótesis simplificadas que se utilizan frecuentemente
al abordar los problemas termodinámicos desde el punto de vista
de la mecánica estadística. Las conclusiones de la termodinámica
son así, por lo general, sumamente precisas. Por otra parte, es
algunas veces poco satisfactorio obtener resultados sin poder ver
en detalle los procesos, de modo que, con frecuencia, es conve­
niente complementar im resultado termodinàmico por lo menos
con una interpretación cinética aproximada.
La primera y segunda ley de la termodinámica tienen su fundamentación estadística en la mecánica clásica. En años recientes,
Nernst agregó una tercera ley, que puede ser interpretada estadís­
ticamente solo en términos de mecánica cuántica. El último capí­
tulo de este libro trata de las consecuencias de la tercera ley.
CAPITULO I
LOS SISTEMAS TERMODINÁMICOS
1. El estado de un sistema y sus transformaciones
En la mecánica, el estado de un sistema en un instante dado
queda completamente definido si se conocen la posición y veloci­
dad de cada masa puntual del sistema. Esto significa que, para
especificar el estado de un sistema compuesto de un número N
de masas puntuales es necestu-io conocer 6N variables.
En termodinámica sé introduce un concepto diferente y mu­
cho más simple. Sería por cierto inconveniente utilizar la defini­
ción dinámica de estado, ya que todos los sistemas con que se
trabaja en termodinámica contienen un gran número de masas
puntuales (los átomos o moléculas) y sería prácticamente imposi­
ble especificar las 6N variables. Por otra parte no tendría sentido
hacerlo, ya que las magnitudes que se utilizan en termodinámica
son propiedades en promedio del sistema; en consecuencia, un
conocimiento detallado del movimiento de cada masa pimtual
sería superfluo.
Para explicar el concepto termodinàmico del estado de un
sistema, examinaremos previamente algunos ejemplos sencillos.
Sistem a compuesto por u n fluido homogéneo químicamente
definido. Es posible medir en este sistema la temperatura t, el
volumen V, y la presión p. La temperatura se mide poniendo un
termómetro en contacto con el sistema durante un intervalo sufi­
ciente para que se produzca el equilibrio térmico. Como se sabe,
la temperatura definida por cualquier termómetro (p. ej., un ter­
mómetro de mercurio) depende de las propiedades particulares de
la sustancia termomètrica utilizada. Por el momento convendre­
mos en usar el mismo tipo de termómetro para todas las medicio­
nes de temperatura, de manera que sean comparables entre sí.
La geometría de nuestro sistema está caracterizada, como es
obvio, no solo por su volumen sino también por su forma. Sin
embargo, la mayoría de las propiedades termodinámicas son in-
dependientes de la forma del sistema y, por lo tanto, es el volumen
el único dato geometrico necesario. Solo en los casos en que la
relación de superficie a volumen es muy grande (p. ej., una subs­
tancia finamente pulverizada), debe considerarse también la su­
perficie.
Para una determinada cantidad de sustancia contenida en el
sistema, la temperatura, el volumen y la presión no son magnitu­
des independientes, pues están relacionadas por una ecuación de
la forma general:
/ (p ,y ,t)= o ,
(1)
conocida como ecuación de estado. Su forma depende de las pro­
piedades características de la sustancia. Cualquiera de las tres
variables en la relación ( 1 ) puede expresarse como una función
de las otras dos resolviendo la ecuación con respecto a la variable
dada. El estado del sistema queda así completamente determinado
por dos cualesquiera de las tres variables p, V, t.
A menudo es conveniente representar gráficamente estas dos
cantidades en un sistema de coordenadas ortogonales. Por ejem­
plo, podemos usar una representación (V ,p ) tomando V a lo
largo del eje de abscisas y p a lo largo del eje de ordenadas. Un
punto en el plano (V, p) definirá así un estado del sistema. Los
puntos que representan estados de igual temperatura yacen sobre
una curva llamada isoterma.
Sistema compuesto por un sólido homogéneo químicamente
definido. En este caso, para definir el estado del sistema podemos
introducir, además de la temperatura í y el volumen V, las pre­
siones actuantes en las distintas direcciones. En la mayoría de
los casos, sin embargo, se supone que el sólido está sujeto a una
presión isotrópica, y se toma en cuenta un único valor de la
misma, como en el caso de un fluido.
Sistem a constituido por una mezcla homogénea de varios
compuestos químicos. En este caso las variables que definen el
estado del sistema no son únicamente temperatura, volumen y
presión, sino también las concentraciones de los diferentes com­
puestos químicos que entran en la mezcla.
Sistem as no homogéneos. Para definir el estado de un siste­
ma no homogéneo es necesario dividirlo en cierto número de
partes homogéneas. Este número puede ser finito en algunos casos
e infinito en otros. Esta última posibilidad, considerada solo ra­
ramente en termodinámica, aparece cuando las propiedades del
sistema, o al menos de algunas partes del mismo, varían con con­
tinuidad de punto a punto. El estado del sistema queda entonces
definido por la masa, la composición química, el estado de agre­
gación, la presión, el volumen y la temperatura de cada una de
las partes homogéneas.
Es obvio que estas variables no son todas independientes en­
tre sí. Así, por ejemplo, la suma de las cantidades de cada ele­
mento químico presente en las diferentes partes homogéneas debe
ser constante e igual a la cantidad total de dicho elemento pre­
sente en el sistema. Además, el volumen, la presión y la tempe­
ratura de cada una de las partes homogéneas que tienen una
masa y una composición química dadas están ligadas por una
ecuación de estado.
Sistem a que contiene partes en m ovim iento. En casi todos los
sistemas que se estudian en termodinámica se supone que las dis­
tintas partes que los constituyen están en reposo, o bien se mue­
ven tan lentamente que se puede despreciar su energía cinética.
Si éste no es el caso, deben especificarse también las velocidades
de las partes para que el estado del sistema quede completamente
definido.
De lo que se ha dicho surge claramente que el conocimiento
del estado termodinàmico no es en modo alguno suficiente para
la determinación del estado dinámico de un sistema. Estudiando
el estado termodinàmico de un fluido homogéneo de volumen y
temperatura dados (la presión queda entonces definida por la
ecuación de estado), se observa que existe un número infinito de
estados de movimiento molecular que le corresponden. A medida
que transcurre el tiempo el sistema pasa sucesivamente por todos
los estados dinámicos que corresponden al estado termodinàmico
dado. Desde este punto de vista se puede decir que un estado
termodinàmico es el conjunto de todos los estados dinámicos por
los cuales pasa rápidamente el sistema como resultado del movi­
miento molecular. Esta definición de estado es más bien abstrac­
ta y de ningún modo única. Es por ello que indicaremos cuáles son
las variables de estado en cada caso particular.
Entre los estados termodinámicos de un sistema debemos
destacar por su importancia los estados de equilibrio. Éstos tienen
la propiedad de no variar en tanto se mantengan constantes las
condiciones externas. Por ejemplo, un gas encerrado en un reci­
piente de volumen constante está en equilibrio cuando la presión
se mantiene constante y su temperatura es igual a la del medio
ambiente.
Deberemos considerar con frecuencia transformaciones de un
sistema desde un estado inicial hasta otro final, pasando por
una sucesión continua de estados intermedios. Si el estado del
sistema puede representarse en un diagrama ( V , p) el gráfico de
la transformación será una curva que une los dos puntos repre­
sentativos de los estados inicial y final.
Se dice que una transformación es reversible cuando los su­
cesivos estados de la transformación difieren de los estados de
equilibrio en cantidades infinitesimales. Una transformación re­
versible se realiza en la práctica variando muy lentamente las
condiciones externas para así permitir que el sistema se ajuste
gradualmente a las nuevas condiciones. Por ejemplo, podemos
producir una expansión reversible en un gas encerrándolo dentro
de un cilindro con un émbolo movible y desplazando éste hacia
afuera muy lentamente. Si lo desplazáramos bruscamente se for­
marían corrientes en la masa gaseosa en expansión y los estados
intermedios dejarían de ser estados de equilibrio.
Si efectuamos en un sistema una transformación reversible
desde un estado inicial A hasta un estado final B, podremos lle­
varlo nuevamente, por medio de la transformación inversa, desde
B hasta A, pasando por la misma sucesión de estados intermedios,
pero esta vez en el orden inverso. Para realizar esta transforma­
ción es necesario simplemente variar en forma muy lenta y en
sentido opuesto al de la transformación original las condiciones
del medio que rodea al sistema. Podríamos así, volviendo a la
experiencia discutida en el párrafo anterior, comprimir el gas
encerrado en el cilindro desplazando el émbolo hacia adentro muy
lentamente hasta llevar el gas a su volumen y estado iniciales. La
compresión se realiza entonces en forma reversible, y el gas pasa
por la misma sucesión de estados intermedios del proceso de
expansión.
Durante una transformación, el trabajo externo que real'za
el sistema puede ser positivo o negativo, es decir, el sistema puede
efectuar trabajo sobre el medio que lo rodea o bien éste sobre el
sistema. Como ejemplo consideremos un cuerpo encerrado en un
cilindro con un émbolo movible del área S (fig. 1).
Si p es la presión del cuerpo sobre las paredes del cilindro, la
fuerza ejercida por el cuerpo sobre el émbolo será entonces pS.
Si se desplaza el émbolo una distancia infinitesimal dh, se efectúa
un trabajo infinitesimal
dL = pSdh,
(2)
dado que el desplazamiento es paralelo a la fuerza. Pero Sdh
4
es igual al incremento, dV, en. volumen del sistema. Por lo tanto
podemos escribir: ^
d i = pdV.
(3)
Fig. 1
Para una transformación finita, el trabajo que realiza el sis­
tema se obtiene integrando la ecuación (3) :
f ’ piiy,
L=
(4)
tomando la integral sobre la toda la transformación.
1 Es obvio q u e (3 ) es válid a en general, independientem ente de cuál
sea la forma del recipiente. C onsiderem os un cuerpo som etido a una presión
uniform e p, encerrado en un recipiente de forma irregular A (fig. 2 ). Consi­
derem os ahora una transform ación infinitesim al de nuestro sistem a, durante
la cual la s paredes del recipien te se m u e v e n desde la posición inicial A a la
posición final B, perm itiendo así la expansión del cuerpo contenido en él.
Sea d<r un elem en to de superficie del recipiente y d n el desplazam iento de
dicho elem en to en dirección norm al a la superficie del recipiente. El trabajo
efectuado sobre el e lem en to de superficie da por la presión p durante el des­
p lazam ien to de la s paredes del recipiente desde la posición A a la posición B
será p dcr dn. El trabajo total realizado durante la transform ación infin itesi­
m al se ob tien e integrando dicha expresión sobre toda la superficie
del
recip ien te dado que p es un a c on stan te, obtenem os:
dL
R esulta evid en te, a l, observar la figura, q u e la variación dV del volum en del
recipiente e stá dada por la integral de superficie.
dV =
j
d<r dn.
Com parando estas dos ecuaciones obtenem os (3 ).
Cuando el estado del sistema puede representarse sobre un
diagrama (V ,p ), el trabajo realizado durante una transformación
tiene una representación geométrica simple.
Consideraremos una transformación desde \in estado inicial
indicado por el punto A hasta un estado final indicado por el punto
B (fig. 3). Esta transformación estará representada por xma curva
que une A y B y cuya forma depende del tipo de transformación
considerada.
Fig. 3
El trabajo realizado durante esta transformación está dado
por la integral
=
ra
Jv
pdV,
(5)
siendo Vx y B b los volúmenes correspondientes a los estados A
y B. Esta integral, y por lo tanto el trabajo efectuado, puede repre­
sentarse geométricamente por el área sombreada en la figura.
Especialmente importantes son las transformaciones para las
cuales los estados inicial y final son los mismos. Éstas son las
llamadas transformaciones cíclicas o ciclos. Un ciclo, por lo tanto,
es una transformación que lleva nuevamente el sistema a su es­
tado inicial. Si el estado del sistema puede ser representado sobre
un diagrama {V, p ) , un ciclo estará representado sobre este dia­
grama por una curva cerrada, como la curva ABCD (fig. 4).
El trabajo, L, efectuado por el sistema durante la transforma­
ción cíclica está dado geométricamente por el área encerrada por
la curva que representa al ciclo. Sean A y C los pvmtos de abscisas
mínima y máxima de nuestro ciclo, y sean A ' y C’ sus proyecciones
respectivas sobre el eje V. El trabajo realizado durante la parte
ABC de la transformación es positivo e igual al área ABCC'A’A.
El trabajo efectuado durante el resto de la transformación, CDA,
es negativo e igual en magnitud al área CC’A ’ADC. La cantidad
total de trabajo positivo realizado es igual a la diferencia entre
estas dos áreas, y, por lo tanto, igual al área limitada por la
curva representativa del ciclo.
Importa hacer notar que el trabajo total realizado es positivo
porque recorremos el ciclo en el sentido de movimiento de las
agujas del reloj. Si lo recorremos en el sentido contrario, el tra­
bajo efectuado estará dado nuevamente por el área limitada por
la curva representativa del ciclo, pero esta vez será negativo.
Una transformación durante la cual el sistema no realiza
trabajo externo se llama transformación isocora. Si suponemos
que el trabajo dL efectuado durante un elemento infinitesimal de
la transformación está dado, de acuerdo con la ecuación (3), por
pdV, para una transformación isocora es dV = O, o por integra­
ción, V = constante. Una transformación isocora es por lo tanto
una transformación de volumen constante. Este hecho justifica
el nombre de isocora. Hay que tener en cuenta, sin embargo, que
el concepto de transformación isocora es más geneí^, dado que
requiere que dL = 0 para la transformación dada, auh cuando el
trabajo dL no se pueda representar por la ecuación (3).
Las transformaciones durante las cuales la presión o tem­
peratura del sistema permanecen constantes se denominan trans­
formaciones isobáricas e isotérmicas, respectivamente.
2. Gases ideales o perfectos
La ecuación de astado de xm sistema compuesto por una cierta
cantidad de gas que ocupa un volumen V a una temperatura t
y una presión p puede ser expresada por una ley analítica muy
sencilla. Obtenemos la ecuación de estado de un gas en su forma
más simple, pasando de la escala empírica de temperatura, í,
xisada hasta ahora, a una nueva escala de temperatura T.
Provisionalmente definimos T como la temperatura indicada
por un termómetro de gas en el cual el gas termomètrico se man­
tiene a muy baja presión constante. T se supone entonces propor­
cional al volumen ocupado por el gas. Es bien sabido que, bajo
estas condiciones, las lecturas de diferentes termómetros de gas
son en gran medida independientes de la naturaleza del gas ter­
momètrico, siempre que éste se halle suficientemente alejado de
la condensación. Más adelante (parágrafo 9), veremos que es
posible, sin embargo, definir esta misma escala de temperaturas
T por medio de consideraciones termodinámicas generales com­
pletamente independientes de las propiedades específicas de los
gases.
La temperatura T es la llamada tem peratura absoluta. Su
imidad se elige de manera que la diferencia entre los puntos de
ebullición y congelación del agua a una atmósfera de presión sea
igual a 100. El punto de congelamiento del agua corresponde
entonces, como es sabido, a la temperatura absoluta 273,1.
La ecuación de estado de un sistema compuesto por m gramos
de un gas cuyo peso molecular es M está dada aproximadamen­
te por:
pV = ^^R T .
(6 )
R es una constante universal (es decir, tiene el mismo valor para
todos los gases: ñ = 8,314 X 10^ erg/grado o
8
(ver par. 3)
R = 1,986 cal/grado). La ecuación ( 6 ) es la llamada ecuación de
estado de un gas ideal o perfecto-, inejuye las leyes de Boyle, GayLussac y Avogadro.
!
.
No existe ningún gas real que cumpla exactamente la ecua­
ción (6 ). Una sustancia ideal que cumple exactamente dicha
ecuación se denomina gas ideal o perfecto.
Para una molécula gramo (o mol) de un gas (esto es, para
un número de gramos de un gas numéricamente igual a su peso
molecular) tendremos m = M, de modo que ( 6 ) se reduce a:
p V = RT.
(7)
De (6 ) y (7) podemos obtener la densidad p del gas en función
de la presión y temperatura:
P -y -R T Para una transformación isotérmica "de un gas ideal (trans­
formación a temperatura constante), tenemos:
p V = constante.
En el diagrama (V, p ), por lo tanto, las transformaciones isotér­
micas de un gas ideal están representadas por hipérbolas equiláte­
ras que tienen como asíntotas a los ejes V y p.
Podemos calcular fácilmente el trabajo realizado por el gas
durante una expansión isotérmica desde un volumen inicial Vi
hasta un volumen final Vo· Este trabajo estará dado (utilizando
las ecuaciones [5] y [ 6 ] ) por:
dV
V
=
log ?1,
M
(9)
p2
en los que pi y po son las presiones inicial y final, respectivamente.
Para un mol de gas tendremos:
L = R T \ o g ^ = R T lo g ^ .
Vi
P2
(10)
Una mezcla de varios gases se gobierna por leyes muy simi­
lares a aquellas que cumple un gas químicamente homogéneo.
Llamaremos presión parcial de uno de los componentes de una
mezcla de gases a la presión que dicho componente ejercería si ocu­
para él solo el volumen total concedido a la mezcla, hallándose a
la misma temperatura que ésta. Podemos ahora expresar la ley
de Dalton para las mezclas de gases en la siguiente forma:
La presión ejercida por uva mezcla de gases es igual a la
suma de las presiones parciales de todos los componentes presen­
tes en la mezcla.
Los gases reales obedecen solo aproximadamente a esta ley,
pero se supone que se cumple exactamente en el caso de gases
ideales.
Problemas
1. Calcular el trabajo realizad o por u n cuerpo que se expand e desde
un volum en inicial de 3,12 litros a un v olu m en final de 4,01 litros a una
presión de 2,34 atm ósferas.
2. Calcular la presión de 30 gram os de h id rógeno dentro de un reci­
p iente de 1 m etro cúbico a la tem peratura de 18^ C.
3. Calcular la densidad y el v o lu m en específico del nitrógen o a la
tem peratura de 0°C .
4. Calcular el trabajo realizad o por 10 gram os de oxígen o e n expansión
isotérm ica a 20° C desd e 1 a 0,3 atm ósferas d e presión.
10
CAPITULO n
LA PRIMERA LEY DE LA TERMODINÁMICA
3. Formulación de la primera ley de la termodinámica
La primera ley de la termodinámica es esencialmente la for­
mulación del principio de conservación de la energía para sistemas
termodinámicos. Como tal, puede ser expresada dejando estable­
cido que la variación en energía de un sistema durante una trans­
formación cualquiera es igual a la suma de energía que el sistema
recibe del medio circundante. Para dar xui significado preciso a
esta formulación, es necesario definir qué se entiende por “ ener­
gía del sistema” y “ energía que el sistema recibe del medio cir­
cundante durante una transformación” .
En sistemas conservativos puramente mecánicos, la energía
es igual a la suma de las energías cinética y potencial, y por lo
tanto es una función del estado dinámico del sistema, porque
conocer este estado dinámico es equivalente a conocer las posi­
ciones y velocidades de todas las masas puntuales contenidas en
el sistema. Si sobre éste no actúan fuerzas externas, la energía
permanece constante. Por lo tanto, si A y B son dos estados su­
cesivos de un sistema aislado, y Ua y Un son las energías corres­
pondientes, entonces:
Ua = Us
Cuando sobre el sistema actúan fuerzas externas, Ua no de­
berá ser necesariamente igual a Ug. Si — L es el trabajo realizado
por las fuerzas externas durante una transformación desde el
estado inicial A hasta el estado final B (-f-í' es el trabajo efectuado
por el sistema), el principio dinámico de conservación de la ener­
gía toma entonces la forma:
U„ — Ua = — L.
( 11)
De esta ecuación surge que el trabajo, L, realizado durante
la transformación depende solo de los estados extremos A y B
11
de ésta y no de la manera particular en que se realiza la trans­
formación de A a B.
Supongamos ahora que desconocemos las leyes de interacción
'entre las varias masas puntuales de nuestro sistema dinámico. Eñ
ese caso, no podemos calcular la energía del sistema cuando éste
se halla en un estado dinámico dado. Utilizando la ecuación (11)
podemos obtener, sin embargo, una .definición empírica de la
energía de nuestro sistema, en la siguiente forma:
Consideraremos en nuestro sistema un estado O elegido ar­
bitrariamente y, por definición, tomaremos su energía como igual
a cero:
Uo =
0.
(1 2 )
En adelante nos referiremos a este estado como el estado de refe­
rencia de nuestro sistema. Consideremos ahora cualquier otro es­
tado A; aplicando al sistema fuerzas externas adecuadas, podre­
mos llevarlo desde el estado de referencia (en el cual suponemos
se hallaba inicialmente) al estado A. Sea
el trabajo que efec­
túa el sistema durante esta transformación (—
es, como antes,
el trabajo que realizan las fuerzas externas sobre el sistema).
Aplicando (11) y esta transformación, y teniendo en cuenta (12),
tendremos que
Ua =
(13)
Esta ecuación puede utilizarse como definición empírica de la
energía Ua de nuestro sistema en el estado A.
Para que la definición (13) tenga significado es obvio que
el trabajo L a debe necesariamente depender solo de los estados O
y A y no del camino particular entre O y A en que se realiza la
transformación. Ya hemos hecho notar que esta propiedad se
deduce de (11). Si se demostrara experimentalmente que dicha
propiedad no se cumple, ello significaría que, o bien la energía no
se conserva ennuestrosistema, o que, además del trabajo mecá­
nico, deben tenerse en cuenta otrasformas detransferencia de
energía.
Supondremos por ahora que el trabajo realizado durante
cualquier transformación por nuestro sistema mecánico depende
únicamente de los estados inicial y final de la transformación, de
modo que podremos usar (13) como definición de la energía.
La ecuación (11) puede obtenerse a partir de la (13) de la
siguiente forma. Una transformación entre dos estados cuales­
quiera A y B puede efectuarse siempre como dos transformacio­
nes sucesivas: primero se realiza la transformación desde A hasta
12
el estado de referencia O, y luego la transformación desde O a B.
Dado que el sistema efectúa durante estas dos transformaciones
las sumas de trabajo — í/x y + ^ b, el trabajo total realizado du­
rante la transformación desde A hasta B (que es independiente
del camino recorrido) es:
L
= —L a
Lb.
De (13) y la ecuación análoga,
Ub = - L b,
obtenemos:
Ub -
Ua = - L ,
la cual es idéntica a (11).
Haremos notar, finalmente, que la definición de la energía
dada por (13) no es única, puesto que depende de la elección
particular del estado de referencia O. Si en lugar de O hubiéramos
elegido un estado de referencia diferente, O’, habríamos obtenido
un valor diferente, U \ , para la energía del estado A . Sin embar­
go, puede demostrarse fácilmente que U \ V Ua difieren solo en
una constante aditiva. La transformación entre los estados O'
y A puede a su vez efectuarse como suma de dos transformaciones
sucesivas, una desde O' a O y la otra desde O hasta A. El trabajo
V a realizado por el sistema cuando éste pasa de O’ a A estará
entonces dado por:
L
a
— L o · o ”1" L
a
,
en la que L q.q es el trabajo que realiza el sistema yendo de O'
hasta O. Tenemos ahora:
Ua =
- L a;
Ua = - L a,
de modo que
U a - U ' a = L o 'O,
lo cual muestra que los valores de la energía obtenidos basándose
en las dos definiciones difiere en la constante Lo o·
Esta constante aditiva indeterminada que aparece en la defi­
nición de la energía es, como se sabe, una característica esencial
del concepto de energía. No obstante, dado que en la práctica solo
13
se consideran diferencias de energía, la constante aditiva no apa­
rece en los resultados finales.
La única hipótesis implícita en la anterior definición de la
energía consiste en suponer que el trabajo total efectuado por el
sistema durante cualquier transformación depende solamente de
los estados inicial y final de ésta. Hemos dicho ya que, si algún
hecho experimental contradijera esta hipótesis, deberíamos ad­
mitir, para seguir sosteniendo la validez del principio de conser­
vación de la energía, la existencia de métodos de intercambio de
energía, distintos del trabajo mecánico, entre el sistema y el
medio circundante.
Tomemos, por ejemplo, un sistema compuesto por una can­
tidad de agua. Consideremos dos estados -<4 y B de este sistema
a la presión atmosférica; sean í,i y tn las temperaturas del sistema
en esos dos estados, respectivamente, con í,i <
Podemos llevar
nuestro sistema desde A hasta B por dos caminos diferentes.
Primer método ; Calentando el agua sobre una llama elevamos
su temperatura desde el valor inicial Ía hasta el valor final Í bEl trabajo externo efectuado por el sistema durante la transfor­
mación es prácticamente cero. Sería exactamente cero si el cambio
de temperatura no estuviera acompañado por un cambio en volu­
men del agua. En realidad el cambio de volumen del agua durante
la transformación es muy pequeño; por lo tanto, la cantidad de
trabajo que se efectúa también es pequeña (ver ecuación [3 ]) y
no será tenida en cuenta en nuestras consideraciones.
Segundo método·. Elevamos la temperatura del agua desde
Í a a tn calentándola por fricción. Con este objeto sumergimos en
ella un pequeño conjunto de paletas adheridas a un eje central,
y haciéndolas girar agitamos el líquido. Observamos que, mientras
las paletas giran, la temperatura del agua sigue aumentando con­
tinuamente. Puesto que el agua ofrece resistencia al movimiento
de las paletas, para mantenerlas en ese estado de movimiento
hasta alcanzar la temperatura final tn debemos efectuar trabajo
mecánico. A esta considerable suma de trabajo positivo realizado
por las paletas sobre el agua, corresponde una suma igual de
trabajo negativo efectuada por ésta en su resistencia al movi­
miento de aquéllas.
Vemos así que el trabajo efectuado por el sistema cuando
pasa del estado A al estado B depende del camino elegido para
realizar la transformación.
Si suponemos que el principio de conservación de la energía
se cumple para nuestro sistema, debemos admitir entonces que
la energía transmitida al agua, en el segundo método, en forma
14
de trabajo mecánico de las paletas en rotación, lo es en el primero
en. una forma no mecánica llamada calor. Llegamos asi a la conclusión de que el calor y el trabajo mecánico son equivalentes; son
dos aspectos diferentes del mismo fenómeno, la energía. En ade­
lante hablaremos también de trabajo eléctrico y trabajo magnético
además de trabajo mecánico. Los dos primeros tipos, sin embargo,
se consideran solo rara vez en termodinámica.
Para expresar de un modo más preciso el hecho de que el calor
y el trabajo son equivalentes, procederemos de la siguiente forma.
Primero encerramos nuestro sistema en un recipiente con
paredes no conductoras del calor para evitar el intercambio de
calor con el medio circundante.* Suponemos, sin embargo, que
puede haber intercambio de trabajo entre el sistema y el medio
circundante (por ejemplo, encerrando el sistema en un cilindro
de paredes no conductoras, pero provisto de un émbolo movible
en un extremo). El intercambio de energía entre el interior y el
exterior del recipiente puede producirse ahora solo en forma de
trabajo, y del principio de conservación de la energía se deduce
que la cantidad de trabajo efectuado por el sistema durante
cualquier transformación depende únicamente de los estados ini­
cial y final de la transformación
Podemos ahora utilizar la definición empírica (13) de la
energía y definir la energía U como función del estado del sistema
solamente.^ Si llamamos
= Un — U,i a la variación de energía^de nuestro sistema que tiene lugar durante una transformación
de.sde un estado A a un estado B, podremos escribir la ecuación
(11) aplicable a nuestro sistema térmicamente aisla:do en la forma:
AU + L = 0.
(14)
1 Solo e s necesario m encionar aquí que no existen aisladores térm icos
perfectos. La aislación térm ica puede obtenerse con bastante aproxim ación
por m ed'o de los bien conocidos m étod os calorim étricos.
^ Sería form alm ente m ás exacto, aunque algo m ás abstracto, expresar
el contenido del párrafo precedente como sifjue:
L as experiencias dem uestran que existen ciertas su bstan cias llam adas
aisla dores térm ic o s que tienen las sigu ien tes propiedades; cuando un sistem a
está encerrado en un aislador térmico de m odo tal que pu ed a haber inter­
cam bio de trabajo entre el interior y el exterior, la cantidad de trabajo
efectuada por el sistem a durante una transform ación dada depende única­
m e n te de los estados inicial y final de la transform ación.
3 D ebem os hacer notar que para hacer aplicable la definición (13)
de la energía de un estado A de nu estro sistem a deberá ser posible transfor­
m ar el sistem a desde un estado de referencia O al estado A m ientras el
sistem a sea térm icam ente aislado. D em ostrarem os m ás adelante (ver par. 13)
que tal transform ación no siem pre e s posible sin intercam bio de calor. En
tales casos, sin embargo, la transform ación opu esta A ~ ^ O puede efectuarse
siempre. El trabajo realizado por el sistem a en esta transform ación inversa
es — L a. Podemos, por 'o tanto, aplicar (13) tam bién a estos casos.
15
Si nuestro sistema no está térmicamente aislado, el primer
miembro (14) será en general distinto de cero, pues en ese caso
puede haber intercambio de energía en forma de calor. Por lo
tanto, reemplazaremos (14) por la ecuación más general:
Al/ + L = Q,
(15)
donde Q es igual a cero para transformaciones realizadas con siste­
mas térmicamente aislados y distinta de cero, en general, en los
demás casos.
Q puedé interpretarse físicamente como la cantidad de ener­
gía que recibe el sistema en formas que difieren del trabajo. Esto
se deduce inmediatamente del hecho de que la variación de ener­
gía, a U, del sistema debe ser igual a la cantidad total de energía
que éste recibe del medio circundante. Pero por (15) es
a U=^
I
j
i
[
— L + Q,
siendo — L la energía recibida en forma de trabajo; por lo tanto
Q representa toda otra forma de energía que recibe el sistema.
Por definición, designaremos ahora a Q como la cantidad de
calor recibido por el sistema durante la transformación,
Para una transformación cíclica, la ecuación (15) adopta una
forma muy simple. Dado que los estados inicial y final de un
ciclo son los mismos, la variación de energía es cero : a U = O y la
(15) se convierte en:
f
^
L = Q.
(16)
De aquí surge que el trabajo efectuado por un sistema durante
una transformación cíclica es igual al calor absorbido por el
sistema.
A esta altura, es importante establecer la relación entre esta
definición abstracta de calor y su definición calorimétrica elemen­
tal. La unidad calorimétrica de calor, la caloría, se define como
la cantidad de calor necesaria para elevar de 14° C a 15“ C la tempe­
ratura de un gramo de agua a la presión atmosférica normal. Para
elevar de 14“ C a 15“ C la temperatura de m gramos de agua a la
presión atmosférica normal se requieren, por lo tanto, m calorías.
Sea Amc la variación de energía de un gramo de agua y 1^ el trabajo
efectuado como resultado de su expansión cuando su temperatura
se eleva de 14“ C a 15° C a la presión atmosférica normal. Para m
gramos de agua, la variación de energía y el trabajo realizado
serán:
16
AÍ/e = mAUc;
Le == mlc.
(17)
Consideraremos ahora un sistema S que experimenta ima
transformación. Con el objeto de medir el calor intercambiado
entre el sistema y los cuerpos que lo rodean, lo ponemos en con­
tacto con un calorímetro que contiene m gramos de agua, a una
temperatura de 14° C. Elegimos la masa de agua de modo que
cuando la transformación se haya completado la temperatura del
agua sea de 15° C.
Como un calorímetro ideal está perfectamente aislado térmi­
camente, el sistema compuesto por S y el agua del calorímetro está
térmicamente aislado durante la transformación. Por lo tanto, po­
demos aplicar a esta transformación la ecuación (14). La varia­
ción total de energía es igual a la suma:
AU =
a U s -f- AU c ,
siendo
la variación de energía del sistema S, y ^Uc la varia­
ción de energía del agua del calorímetro. Análogamente, para el
trabajo total realizado tenemos:
L = Ls
Le.
Por (14) se obtiene:
^Us -}■
Ls
Le = 0;
o, por (17)
AUs
Ls = -- {^Ue -|- Le)
= — m (AUc + U) ·
Pero de acuerdo con la definición (15), AU¡
es la cantidad de
calor Qs recibido por el sistema S. Entonces tenemos :
Q, = — m(AWc + í<).
(18)
que nos indica que la cantidad de calor es proporcional a m.
Por otra parte, en calorimetría, el hecho de que la tempe­
ratura de m gramos de agua de un calorímetro se haya elevado de
14° C a 15° C significa que han sido transferidas del sistema S al
calorímetro m calorías; es decir, que el sistema S ha recibido — m
calorías, o bien que Qs, expresado en calorías, es igual a — m.
Comparando con (18) vemos también que la cantidad de calor, tal
como está dada por la definición (15), es proporcional a la misma
cantidad cuando está expresada en calorías. La constante de pro­
porcionalidad es (A«c + íc) ·
De acuerdo con (15), el calor se mide en unidades de energía
(ergios). La relación constante entre ergios y calorías ha sido
medida por muchos investigadores, quienes hanencontrado que:
1 caloría = 4,185 X 10^ergios.
(19)
En adelante expresaremos generalmente lasmedidas decalor en
unidades de energía.
La ecuación (15), que es una formulación precisa de la equi­
valencia entre calor y trabajo expresa la primera ley de la termo­
dinámica.
4. Aplicación de- la primera ley a sistemas cuyos estados pueden
representarse en im diagrama i y , p )
Aplicaremos ahora la primera ley de la termodinámica a
un sistema, un fluido homogéneo, cuyo estado puede definirse en
términos de dos cualesquiera de las tres variables V, p, y T. Cual­
quier función de estado del sistema, como, por ejemplo, su energía,
U, será \ma función de las dos variables elegidas para representar
dicho estado.
Para evitar confusiones en lo que respecta a cuáles son las
variables independientes, cuando es necesario trabajar con deri­
vadas parciales, encerraremos el símbolo de derivada parcial en
un paréntesis y pondremos al pie la variable que se mantiene
constante en la derivación parcial. De esta manera
iy
significa derivada de U con respecto a T, manteniendo a V cons­
tante, cuando tomamos T y V como variables independientes.
Hay que tener en cuenta que la expresión arriba indicada es en
general distinta de
/d U \
j
dado que en el primer caso es el vo­
lumen el que se mantiene constante, mientras que en el segundo
lo que se mantiene constante es la presión.
Consideremos ahora una transformación infinitesimal de
nuestro sistema, es decir, una transformación para la cual las varia­
bles independientes sufren solo variaciones infinitesimales. Aplica­
mos a esta transformación la primera ley de la termodinámica como
está expresada en la ecuación (15). En lugar de á.U, L y Q, debe­
mos escribir dU, dL y dQ, para indicar la naturaleza infinitésima^
de dichas cantidades. Obtenemos entonces :
18
d ll + dL = dQ.
(20)
Como en nuestro sistema dL está dado por (3), tenemos;
dU + pdV = dO.
(21)
Si elegimos T y V como variables independientes, U se con­
vierte en una función de esas variables, de manera que:
y la ( 21) se convierte en:
(22)
Del mismo modo, tomando T y p como variables independientes
obtenemos:
dp
=
dQ. (23)
Finalmente, tomando V y p como variables independientes, te­
nemos:
dV = dQ.
(24)
La capacidad térmica de un cuerpo es, por definición, la rela­
ción, dQ/dT, entre la cantidad infinitesimal de calor dQ absorbida
por el cuerpo y el incremento infinitesimal de temperatura dT
producido por ese calor.* En general, la capacidad térmica de
un cuerpo será distinta si éste se calienta a volumen constante o
a presión constante. Sean Cy y Cp las capacidades térmicas a
volumen constante y a presión constante respectivamente.
De la (22) podemos obtener una expresión simple para Cy.
* En otras obras sobre el m ism o tem a el lector encontrará la exp re^ ón
"capacidad calórica” (h e a t c a p a city en in glés) referida a la definición qüe
antecede. En esta edición se ha respetado la term inología usada por Fermi
( th e rm a l c a p a c ity ) traduciéndola literalm ente. (N. del R.)
19
Para una transformación infinitesimal a volumen constante
dV =« 0, por lo tanto,
Análogamente, usando la (23), obtenemos para Cp la siguiente
expresión:
<»
El segundo término de la derecha representa el efecto del
trabajo efectuado durante la expansión, sobre la capacidad tér­
mica. En (25) no aparece ningún término análogo, porque en
ese caso, como el volumen se mantiene constsmte, no hay ex­
pansión.
Se llama calor específico de una sustancia a la capacidad tér­
mica de un gramo de la misma. El calor molecular es la capacidad
térmica de un mol. Las fórmulas (25) y (26) nos dan el calor
específico y molecular a volumen constante y a presión constante,
siempre que, en lugar de tomar una cantidad cualquiera de sus­
tancia, tomemos un gramo (para el caso del calor específico) y
un mol (para el del calor molecular).
5. Aplicación de la primera ley a los gases
EIn el caso de un gas, podemos expresar en forma explícita
la dependencia entre la energía y las variables de estado. Elegi­
mos como variables independientes a T y V, y probamos, en primer
lugar, que la energía es solo función de la temperatura T y no
depende del volumen V. Esta propiedad, como muchas otras
propiedades de los gases, se cumple aproximadamente para los
gases reales y se considera que se cumple exactameiite para gases
ideales. En el parágrafo 14 deduciremos, partiendo de la segimda
ley de la termodinámica, que la energía de cualquier cuerpo que
cumple la ecuación de estado (7), de un gas ideal, debe ser inde­
pendiente del volumen V. A esta altura, sin embargo, daremos
una comprobación experimental de esta proposición para un gas.
Se trata del experimento de Joule.
Dentro de un calorímetro, Joule colocó un recipiente provisto
de dos cámaras, A y B, comunicadas por un tubo (fig. 5). Llenó
con un gas la cámara A e hizo el vacío en B. Previamente, colocó
20
una llave de paso en el tubo de conexión para poder aislar entre
sí las dos cámaras. Cuando el termómetro introducido en el calo­
rímetro indicaba que se había alcanzado el equilibrio térmico,
Joule abrió la llave para permitir el desplazamiento del gas desde
A hacia B hasta que la presión en todo el recipiente fuera la
misma. Observó entonces que solo se había producido un ligero
cambio en la lectura del termómetro. Esto significaba que, prác­
ticamente, no se había producido transferencia de calor del calorí­
metro a la cámara o viceversa. Se considera que si este experimento
pudiera efectuarse con un gas ideal, no habría ningún intercambio
de temperatura.
£
Fig. 5
Aplicaremos ahora la primera ley a la anterior transforma­
ción. Dado que Q = O, tenemos, por la ecuación (15), que para
el sistema constituido por las dos cámaras y el gas encerrado en
ellas :
AU + L = 0,
donde L es el trabajo realizado por el sistema y
la variación
de energía del sistema. Como los volúmenes de las dos cámaras
A y B que componen nuestro sistema no varían durante el experi­
mento, el sistema no puede efectuar trabajo externo, es decir qu§
L = 0. Por lo tanto.
AU = 0;
la energía del sistema y, en consecuencia, la energía del gas no
varían. Consideremos ahora el proceso en su conjunto. Inicial­
mente el gas ocupaba el volumen A , mientras que al final del
proceso llenaba las dos cámaras A y B; es decir que durante la
transformación se produjo un cambio de volumen del gas. El ex­
perimento demostró, sin embargo, que no se produjo ninguna
variación en la temperatura del gas. Como durante el proceso
tampoco hubo variación de energía, llegamos a la conclusión de
que una variación de volumen a temperatura constante no produ­
ce variación en la energía. En otras palabras, la energia de un
gas ideal es solo función de la temperatura y no del volum en del
gas. Para la energía de un gas ideal podemos escribir entonces:
U^V{T).
I.
(27)
Para determinar la forma de esta función haremos uso de la com­
probación experimental de que el calor específico a volumen cons­
tante de un gas depende solo ligeramente de la temperatura; con­
sideraremos que para un gas ideal el calor específico es una cons­
tante. En este parágrafo nos referiremos siempre a un mol de gas;
Gy y Cp representarán entonces los calores moleculares a volumen
constante y a presión constante, respectivamente.
Dado que 17 depende únicamente de T, no es necesario especi­
ficar que el volumen debe mantenerse constante en la derivada
en (25), y por lo tanto para un gas ideal podemos escribir:
dU
C v = -----
dT
(28)
Como se considera a Cy una constante, podemos integrar de in­
mediato y obtenemos:
U = C yT -^ W ,
(29)
en la que W es una constante de integración que representa la
energía existente en el gas a la temperatura del cero absoluto.^
Para un gas ideal, la ecuación (21), que expresa la primera
ley de la termodinámica para transformaciones infinitesimales,
toma la forma:
Cy dT + pdV = dQ.
(30)
Diferenciando la ecuación característica (7) para un mol de un
gas ideal, obtenemos:
pdV + V d p ^ R d T .
(31)
^ Esta con stan te aditiva solo afecta los resultados fin a les cu an d o se
producen transform aciones qu ím icas o cam bios en los estad os d e agregación
de las substancias. (Ver, p. ej. el cap. VI.) En todos los otros ca so s p od em os
considerar la con stan te aditiva igual a cero.
22
Sustituyendo ésta en (30), tenemoá:
{Cy
+
R)dT - Vdp = dQ.
(32)
Como dp = 0 para una transformación a presión constante, esta
ecuación nos da:
Es decir que la diferencia entre los calores moleculares de un gas
a presión constante y a volumen constante es Igual a la constante
R de los gases.
El mismo resultado puede obtenerse de (26), (29) y (7). En
efecto, para un gas ideal tenemos por (29) y (7) :
/dU \
dU
^
\W J , - d T ~ ^ ^ ’
/a F \
_ ( à RT\ _ R
\ d T jp - \ d T p j ,
p-
Sustituyendo estas expresiones en (26), obtenemos nuevamen­
te (33).
Puede demostrarse, aplicando teoría cinética, que:
Cy = ^ R para un gas monoatómico; y
Cy = ^ R para un gas diatómico.
(34)
Considerando esos valores, que coinciden muy bien con los expe­
rimentales, deducimos de (33) que;
Cp = ^ R para un gas monoatómico; y
Cp = ^ R para un gas diatómico.
(35)
Si ponemos
Cp
Cy
+
^
R
23
obtenemos también:
K = ^ para un gas monoatómico; y
K = i para un gas diatómico.
(37)
6. Transformaciones adiabáticas de un gas
Se dice que una transformación de un sistema termodinàmico
es adiabática si es reversible y si el sistema está térmicamente
aislado de tal modo que no pueda haber intercambio de calor
entre él y el medio circundante mientras se realiza la transfor­
mación.
Podemos expandir o comprimir adiabáticamente un gas en­
cerrándolo en un cilindi'o con paredes no conductoras y provisto
de un émbolo que desplazamos hacia afuera o hacia adentro muy
lentamente. Cuando un gas se expande adiabáticamente realiza
trabajo externo, de manera que L en la ecuación (15) es en este
caso positivo. Dado que el gas está térmicamente aislado, Q = 0
y. por lo tanto, At/ debe ser negativa. Es decir que la energía de
un gas disminuye durante una expansión adiabática. Como la
energía está relacionada con la temperatura a través de la ecua­
ción (29), una disminución en la energía significa también una
disminución en la temperatura del gas.
Con el objeto de, obtener una relación cuantitativa entre la
variación de temperatura y la de volumen resultantes de la ex­
pansión adiabática de un gas, observamos que, como dQ — O, la
ecuación (30) se convierte en;
CydT + pdV = 0.
Por medio de la ecuación de estado pV = RT, podemos eliminar
p de la anterior ecuación y obtendremos:
CvdT + ^ d V = 0 ,
dT
T
24
RdV_
Cv V ~
Integrando tendremos:
R
log T -j------- log V = constante.
Cv
Pasando de logaritmos a números obtenemos:
R
yycv ^ constante.
Utilizando la (36) podemos escribir la ecuación precedente en
la forma:
'fVK-i constante.
(38)
Esta ecuación nos dice cuantitativamente como una variación
adiabática en el volumen de un gas ideal determina un cambio én
su temperatura.Por ejemplo, si expandimosadiabáticamente un
gas diatómicoa dos veces su volumen inicial, veremos por (38)
(suponiendo de acuerdo con [37] que K = - ^ ) que la temperatura
se reduce en la relación 1 : 2°·* = 1 : 1,32.
Utilizando la ecuación de estado pV = RT, podemos expresar
la ecuación (38) de una transformación adiabática de la siguiente
manera :
pV^ == constante,
(39)
K-l
constante.
(40)
P
Debemos comparar la ecuación (39) con la ecuación,
pV = constante,
de una transformación isotérmica. En un diagrama iV ,p ) , las
isotermas son una familia de hipérbolas equiláteras; las lineas
correspondientes a las adiabáticas, representadas por la ecuación
(39), son cualitativamente similares a hipérbolas, pero su pen­
diente es más pronunciada, ya que íí > 1.
En la figura 6 se han representado isotermas y adiabáticas,
las primeras en línea llena y las últimas en línea punteada.
25
Una aplicación simple e interesante de la expansión adiabá­
tica de un gas es el cálculo de la dependencia de la temperatura
de la atmosfera con la altura sobre el nivel del mar. La razón
principal de esta variación de la temperatura con la altura sobre
el nivel del mar es que existen en la troposfera corrientes de
convección que continuamente transportan aire de las regiones
más bajas a las más altas y viceversa. Cuando el aire de las re­
giones a nivel del mar se eleva a las más altas de menor presión,
se expande. Dado que el aire es mal conductor del calor, es muy
poco el calor que recibe o entrega durante la expansión, de mane­
ra que podemos considerar que ésta se realiza adiabáticamente.
En consecuencia, la temperatura del aire ascendente decrece. Por
otra parte, el aire de las regiones superiores de la atmósfera sufre
una compresión adiabática y, por consiguiente, un aumento en su
temperatura, al desplazarse a las regiones más bajas.
Fig. 6
Para calcular la variación de temperatura consideramos una
columna de aire de sección transversal unitaria, y fijamos nuestra
atención sobre un elemento de columna de altura dh, y cuya cara
inferior se encuentra a una distancia h sobre el nivel del mar.
Si es p la presión sobre la cara inferior, la presión sobre la cara
superior será entonces p + dp, siendo dp la variación en la presión
debida al peso del aire en el elemento de columna. Si g es la ace­
leración de la gravedad y p la densidad del aire, el peso del aire
en el elemento será pgdh. Como la presión disminuye a medida
que aumenta la altura, tenemos;
dp — — pgdh;
o, recordando (8 ),
dp = —
i
26
R T
(41)
donde M es el peso molecular medio del aire; M = 28,88, La
derivada logarítmica de (40) nos da:
dT
K — ld p
T
K
p
Ésta, junto con la ecuación precedente, da:
dT
K — lg M
(42)
Si consideramos que
V.
í7 = 980,665 cm/s=;
M = 28,88 gm;
X IQ·^ erg/grado,
R = 8,214
obtenemos :
dT
— 9,8
X
10“®grados/cm.
dh
— 9,8 grados/kilómetro.
Este valor es en realidad algo mayor que la disminución de
temperatura con la altura que se observa en promedio. La dife­
rencia se debe fundamentalmente al hecho de no haber tenido
en cuenta el efecto de la condensación de vapor de agua sobre las
masas de aire en expansión.
Problemas
1. Calcular la variación d e energía de un sistem a que efcctúa un tra­
b ajo de 3,4 X 108 ergios y absorbe 32 calorías en form a de calor.
2. ¿C uántas calorías absorben 3 m oles de un gas ideal que se expande
isotérm icam ente desde u n a presión inicial de 5 atm ósferas h asta una presión
final de 3 atm ósferas, a la tem peratura de 0"C?
3. Un m ol de ga s ideal diatóm ico efectúa una transform ación desde un
e stad o inicial para el cual la tem peratura y el volum en son, respectivam ente,
291" K y 21.000 cm“, h asta un e sta d o final para el cual la tem peratura y
v olum en son 305° K y 12.700 cm ’. La transform ación se representa en el d ia­
gram a (V. p ) por un a lín ea recta. D eterm inar el trabajo efectuado y el calor
absorbido por el sistem a.
4. Un ga s diatóm ico se expand e adiabáticam ente h asta un volum en
1,35 v eces su volum en inicial. La tem peratura inicial es 18° C. Hallar la
tem peratura final.
27
CAPÍTULO m
LA SEGUNDA LEY DE LA TERMODINÁMICA
7. Formulación de la segunda ley de la termodinámica
í
La primera ley de la termodinámica surgió como resultado de
la imposibilidad de construir una máquina capaz de crear energía.
Esta primera ley, sin embargo, no impone limitaciones a la po­
sibilidad de transformar unas formas de energías en otras. Por
ejemplo, teniendo en cuenta únicamente la primera ley, existe
siempre la posibilidad de transformar el calor en trabajo o el
trabajo en calor con tal que la cantidad total de calor sea equiva­
lente a la cantidad total de trabajo.
Esto es realmente cierto para la transformación de trabajo
en calor. Un cuerpo, cualquiera sea su temperatura, puede siem­
pre ser calentado por fricción y recibirá, en forma de calor, una
cantidad de energía exactamente igual al trabajo efectuado. Aná­
logamente, la energía eléctrica puede siempre ser transformada
en calor haciendo pasar una corriente eléctrica a través de una
resistencia. Existen, sin embargo, limitaciones muy definidas pa­
ra la posibilidad de transformar el calor en trabajo. Si así no
fuera, sería posible construir una máquina que podría, enfriando
los cuerpos circundantes, transformar en trabajo el calor tomado
del medio ambiente.
Como la cantidad de energía térmica que pueden suministrar
el suelo, el agua y la atmósfera es prácticamente ilimitada, dicha
máquina sería, en la práctica, equivalente a un m óvil -perpetuo.
Es lo que se conoce en termodinámica como m óvil perpetuo de
segunda especie.
La segunda ley de la termodinámica descarta la posibilidad
de construir un m óvil perpetuo de segunda especie. Para dar una
formulación precisa de esta ley definiremos qué se entiende por
una fuente de calor a temperatura dada.
Se define como una fuente de calor de temperatura í a un
cuerpo que tiene en todos sus puntos la temperatura í y se en­
cuentra en condiciones tales que puede intercambiar calor, pero no
28
trabajo, con el medio ambiente. Como ejemplos podemos consi­
derar cuerpos encerrados en recipientes rígidos o cuerpos cuyas
variaciones de volumen son despreciables. Una masa de agua que
se encuentra a una temperatura t en todos sus puntos, puede
considerarse como una fuente de calor, puesto que su volumen
permanece prácticamente constante.
Podemos ahora formular la segunda ley de la termodinámica
como sigue:
Es imposible efectuar una transformación cuyo único resul­
tado final sea transformar en trabajo « í calor extraído de una
fuente con la m ism a temperatura en todos sus puntos?· (Postulado
de Lord Kelvin.)
La evidencia experimental en favor de esta ley consiste fun­
damentalmente en el fracaso de todos los esfuerzos realizados pa­
ra construir un m óvil perpetuo de segunda especie,
La segunda ley puede también ser expresada como sigue:
Es imposible efectuar una transformación cuyo único resul­
tado final sea transferir calor de un cuerpo a una temperatura
dada a un cuerpo a una temperatura mayor. (Postulado de Clausius,)
Hasta ahora, hemos utilizado solamente una escala empírica
de temperaturas. Para poder dar un significado preciso al postu­
lado de Clausius, debemos definir previamente qué se entiende al
decir que un cuerpo está a mayor temperatura que otro. Si pone­
mos en contacto térmico dos cuerpos que se hallan a distintas tem­
peraturas, el calor fluye espontáneamente, por conducción, de uno
a otro cuerpo. Diremos, por definición, que de ambos cuerpos el que
se halla a mayor temperatura es aquel del cual fluye el calor.
Convenido esto, podemos formular el postulado de Clausius así:
1
U na parte esencial del postulado de Lord K elvin es que la transfor­
m ación del calor en trabajo sea el único resultado final del proceso. Cierta­
m ente, no e s im posible transform ar en trabajo el calor que se tom a de una
fuente a tem peratura uniform e, siem pre que se produzca al final del proceso
algún otro cam bio e n el estad o del sistem a.
Considerem os, por ejem plo, la expansión isotérm ica de un gas ideal que
se m an tien e en con tacto térm ico con una fuente de calor a la tem peratura T.
Dado que la energía del gas depend e ún icam ente de la tem peratura, y que la
tem peratura no cam bia du ran te el proceso, debe ser ¿JJ — 0. Por la primera
ley, ecuación (1 5 ) , ob ten em os entonces L = Q. E s decir, el trabajo, L, rea­
lizado por el gas en exp an sión e s igual al calor Q que el m ism o absorbe de la
fuente. Se ha producido así una com pleta transform ación del calor, Q, en
trabajo, L. Sin em bargo, e sto no contradice el postulado de Kelvin, ya que
la transform ación de Q en L no es el único resultado final del proceso. El
volum en que ocupa el gas al final del proceso e s m ayor que el que ocupaba
al com ienzo.
Si el calor fluye por conducción de un cuerpo A a otro B, es
imposible una transformación cuyo único resultado final sea trans­
ferir calar de B a A.
I
’
*j
j
iI
'¡
||
Debemos probar ahora la equivalencia de los postulados de
Qausius y Kelvin. Para hacerlo, demostraremos que sí el postulado de Clausius no fuera válido, tampoco lo sería el de Kelvin y
viceversa.
Supongamos en primer lugar que el postulado de Kelvin no
sea válido. En ese caso podríamos efectuar una transformación
cuyo único resultado final fuera transformar totalmente en trabajo una cantidad definida de calor tomada de una única fuente
a la temperatura t^. Por medio de fricción podríamos transformar nuevamente dicho trabajo en calor y utilizar este calor para
elevar la temperatura de un cuerpo dado, independientemente de
cual haya sido su temperatura inicial, ío. En particular podríamos
tomar ts mayor que ti. El único resultado final de este proceso
sería, entonces, la transferencia de calor de un cuerpo (la fuente
a la temperatura ti) a otro cuerpo que se halla a la temperatura
ts, mayor que ti. Esto sería una violación del postulado de Clau­
sius.
La segunda parte de la demostración de la equivalencia entre
los dos postulados requiere una discusión previa de las posibili­
dades de transformar el calor en trabajo. Haremos esta discusión
en el parágrafo siguiente.
8. El ciclo de Carnet
Como, de acuerdo con el postulado de lord Kelvin, es impo­
sible transformar en trabajo el calor que se toma de una única
fuente a temperatura uniforme mediante una transformación que
no produzca ningún otro cambio en los sistemas que intervienen
en ella, para realizarla necesitamos por lo menos dos fuentes a
dos temperaturas distintas, ti y t-j. Si contamos con dichas fuen­
tes, podemos transformar el calor en trabajo por medio del pro­
ceso siguiente, denominado ciclo de Carnot.
Consideremos un fluido cuyo estado pueda representarse so­
bre un diagrama (V, p) y estudiemos dos adiabáticas y dos iso­
termas correspondientes a las temperaturas ti y to. Estas cuatro
curvas se interceptan en los puntos A, B, C y D, como muestra
la figura 7. Sean .¡45 y CD las isotermas de temperaturas ts y ti
respectivamente. AC y BD son las adiabáticas. La transformación
cíclica reversible ABDCA es lo que llamamos un dclo de Carnot.
30
El siguiente ejemplo ilustrará cómo puede realizarse en la
práctica un ciclo de Carnot. Encerramos nuestro fluido en un
recipiente cilindrico de paredes laterales no conductoras y provisto
de un émbolo no conductor en un extremo, de manera que el
Fig. 7
calor solo puede salir o entrar en el cilindro a través del otro
extremo (la base) que tomamos como conductora del calor. Sean
ti y ¿2 dos fuentes de calor suficientemente extensas de modo que
su temperatura no sufra una alteración sensible si les agregamos
o quitamos cualquiei· cantidad finita de calor. Sea tn mayor que ti.
Suponemos que el volumen y la presión del fluido en el cilin­
dro son inicialmente Va y Pa respectivamente, correspondiendo en
la figura 7 al punto A. Como este punto está sobre la isoterma
correspondiente a la temperatura Í2, la temperatura del fluido es
inicialmente igual a íj. Por lo tanto, si colocamos el cilindro sobre
la fuente ío, no se producirá transferencia de calor (fig. 8, A ).
Manteniendo el recipiente sobre la fuente U, levantamos el pistón
muy lentamente incrementando así el volumen en forma reversible
hasta que haya alcanzado el valor V¡, (fig. 8 , B). Esta parte de
la transformación está representada por el segmento AB de la iso­
terma tn. El estado de nuestro sistema está representado ahora
por el punto B en la figura 7.
Colocamos ahora el cilindro sobre un aislador térmico e incre­
mentamos el volumen muy lentamente hasta que alcanza el valor
Vfí (fig. 8 , D), Como durante el proceso el sistema está térmica­
mente aislado, se representa aquél en la figura 7, con el segmento
de adiabática BD. Durante esta expansión adiabática, la tempe­
ratura del fluido decrece de t^ a íi, y el estado del sistema está
dado ahora por el punto D en la figura 7.
Poniéndo el cilindro sobre la fuente íi, comprimimos ahora
el fluido muy lentamente a lo largo de la isoterma DC (fig. 7) has­
ta que su volumen disminuye a Ve (fig. 8, C ). Por último colo­
camos nuevamente el cilindro sobre el aislador térmico y com-
31
primimos muy lentamente el fluido en forma adiabática a lo largo
del segmento CA hasta que su temperatura se eleva a Í3. El sis­
tema habrá vuelto a su estado inicial, que está dado en la figura 7
por el punto A (fig, 8, A ).
Aisla'ior
Aisla­
dor
ti
D
B
Fig. 8
Mientras se efectúa la expansión isotérmica representada por
el segmento AB, el sistema absorbe una cantidad de calor Q2
de la fuente Í2· Durante la compresión isotérmica representada
por el segmento DC, el sistema absorbe una cantidad de calor — Qi
de la fuente íi; es decir, entrega a la fuente íi una cantidad de
calor Qi. La cantidad total de calor absorbido por el sistema du­
rante el ciclo es Q2 — Qi- Sea L el trabajo realizado por el siste­
ma durante la transformación. Este trabajo es igual al área limi­
tada por el ciclo en la figura 7. Utilizando la ecuación (16), que
expresa la primera ley de la termodinámica para un ciclo, tenemos:
L = Q2 - Q
1
(43)
.
Esta ecuación expresa que solo parte del calor que absorbe
el sistema de la fuente de mayor temperatura se transforma en
trabajo mediante el ciclo de Carnot; el resto del calor, Qi, en vez
de ser transformado en trabajo, es entregado a la fuente que se
halla a menor temperatura.
Definimos como eficiencia del ciclo de Carnot a la relación
_
L _ Qi — Qi _ -i _
Q ,~
Q2
"
(44)
Q2 ’
entre el trabajo realizado por el ciclo y el calor absorbido de la
fuente a mayor temperatura.
32
Dado que el ciclo de Carnot es reversible, puede efectuarse en
sentido inverso. Esto puede llevarse a cabo realizando, todas las
transformaciones descritas anteriormente, pero en sentido opuesto.
En ese caso, el ciclo absorbe el trabajo L en lugar de producirlo,
y absorbe la cantidad de calor Qi a la temr< i·atura ti, entregando
la cantidad de calor Q2 a la temperatura í-.
Como primera aplicación del ciclo de Carnot completaremos la
demostración de la equivalencia de los postulados de Clausius y
Kelvin, probando que si el de Clausius no fuese válido, tampoco
lo sería el de Kelvin.
Supongamos que, en contradicción con el postulado de Clau­
sius, fuera posible transferir una cierta cantidad de calor Q2 de
una fuente a la temperatura
a una fuente a temperatura mayor,
Í2, de tal modo que no se produjera ningún otro cambio en el
estado del sistema. Con la ayuda de un ciclo de Carnot podríamos
entonces absorber la cantidad de calor Q 2 y producir un trabajo L.
Como la fuente a la temperatura ¿2 recibe y entrega igual canti­
dad de calor, no sufre ningún cambio en su estado final. El proce­
so recién descrito tendría como único resultado final la transfor­
mación en trabajo del calor extraído de una fuente que se halla
a igual temperatura ¿i en todos sus puntos. Esto contradice el
postulado de Kelvin.
9. La temperatura termodinámica absoluta
En el parágrafo precedente hemos descrito una máquina cí­
clica reversible, el ciclo de Carnot, que absorbiendo una cantidad
de calor Q2 de una fuente a temperatura ¿2 y entregando una can­
tidad de calor Qi a una fuente a la temperatura menor íi, efectúa
un trabajo L durante cada uno de los ciclos. Diremos que dicha
máquina trabaja entre las temperaturas íi y ¿2·
Consideremos ahora una máquina que trabaja entre esas tem­
peraturas (¿1 < Í2). Sea L el trabajo efectuado por la máquina
durante cada ciclo y sean Q2 y Qi las cantidades de calor por ciclo
absorbidas a la temperatura to y expelidas a la temperatura ti,
respectivamente. Esta máquina no debe ser necesariamente un
ciclo de Carnot. La única condición que le imponemos es que
sea cíclica, es decir, que al final del proceso debe volver a su estado
inicial.
Se puede demostrar fácilmente que si L > O, esto es, si la má­
quina realiza trabajo positivo, entonces será Qo > O y Qi > 0 .
Supongamos en primer lugar que Qi ^ 0. Esto significaría
que la máquina absorbe de la fuente ti una cantidad de calor Qi
en el transcurso del ciclo. Podríamos entonces poner en contacto
térmico las dos fuentes y dejar fluir espontáneamenie, por con­
ducción, de la fuente más caliente fo a la niás fría ti, hasta que
ésta haya recibido exactamente la misma cantidad de calor que
entregó a la máquina durante el ciclo. La fuente ti no sufriría de­
este modo ninguna modificación y la máquina volvería a su estado
inicial. El único resultado final de este proceso sería entonces la
transformación en trabajo del calor absorbido de una única fuente
a temperatura t·^ en todos sus puntos. Dado que esto contradice el
postulado de Kelvin, deberá ser Qi > 0.
Demostrar que Q2 > O es ahora muy simple. Como nuestra
máquina vuelve a su estado inicial después del ciclo, tenemos por
la primera ley (ver ecuación (1 6 )):
L = Qz — Q i .
Pero como tomamos L > O y hemos demostrado que Qi > O, de­
berá ser también Q2 > 0 .
Consideremos ahora una segunda máquina que trabaja entre
las mismas temperaturas íi y Í2 y para la cual U, Q’ 2 y Q’i son las
cantidades correspondientes a L, Qa y Qi de la primera máquina.
Demostraremos el siguiente teorema fundamental:
a) Si la primera máquina es reversible ^ entonces:
h
í
b) Si la segunda máquina es reversible, será:
9? = :9Í
Q i
(46)
Q{
En la primera parte del teorema (a) , no hacemos ninguna
hipótesis con, respecto a la segunda máquina; ésta puede ser re­
versible o no sei:lo.
Si aplicamos la ecuación (16) (caso especial de la primera
ley para un ciclo) a nuestras dos máquinas, vemos que el trabajo
realizado por cada una de ellas durante un ciclo debe ser igual
a la diferencia entre el calor recibido de la fuente ío y el entregado
a la fuente ti. Tendremos entonces:
2
D enom inam os m áquina “reversible” a una m áquina que opera en un
ciclo reversible.
34
L = Qo— Q„
(47)
L’ ==Q\_ — Q \.
(48)
y
La relación Qz/Q’z puede ciertamente aproximarse por medio
de un número racional tan exactamente como se quiera. Pode­
mos por lo tanto poner:
Q-2
N’
Q’2
N
— = -
(49)
donde N y N ’ son enteros positivos.
Consideremos ahora un proceso consistente en N ’ ciclos de la
segunda máquina y N ciclos inversos de la primera. Éste es un
proceso permitido, ya que hemos supuesto que la primera máquina
es reversible. Cuando se opera en sentido inverso, la primera má­
quinaabsorbedurante cada ciclo la cantidad detrabajo L y en­
trega alafuente ¿2 lacantidad de calor Q2 a la vez queabsorbe de
la fuente tj la cantidad de calor Qj.
El trabajo total efectuado por ambas máquinas durante el
complejo proceso descrito más arriba es:
Ltoia, = N ’ L' — iVL.
La cantidad total de calor absorbido de la fuente to es:
Q 2 , tota. ^ N ' Q ’, — N Q ,.
La cantidad total de calor entregado a la fuente ti es:
Ql, to u i= N 'Q ’i —
De (47) y (48) obtenemos inmediatamente:
total ----Ql» totnl·
Ltotal =
Pero de (49) deducimos que
Q 2,
total = 0 .
(50)
Ltotal ----------- Q l total-
(51)
Por lo tanto,
La ecuación(50) indica que el proceso completo no produce
ningún intercambio de calor a la temperatura mayor tn; y ja ecua-
35
ción (51) establece que el calor absorbido de la fuente ti (igual
a — Qi, totaü) es transformado en el trabajo Ltotni·
Dado que el proceso completo está compuesto por varios cidos de cada máquina, ambas volverán a su estado inicial al término de dicho proceso. De aquí surge que Liotai no puede ser positivo; si lo fuera, el único resultado final de todo el proceso sería
la transformación en trabajo, Ltotai, del calor, — Qi, totni, absorbido de una fuente a la temperatura ti en todos sus puntos. Esto
estaría en contradicción con el postulado de Kelvin. Por lo tanto
debe ser:
;
<¡
1
¿
j
I
i'total — O·
Por la ecuación (51), esta desigualdad es equivalente a
Qi, tota] — 0 ;
y teniendo en cuenta la expresión Qi, totai, tenemos:
1SI’Q \ ^ A/Qi.
Si eliminamos de esta expresión N ’ y N con la ayuda de la
ecuación (49), y teniendo en cuenta que todas las cantidades en
(49) son positivas, obtenemos:
QzQi ^ QiQit
o
9 i> 9 í
Q i ~ Q Í ’
que es idéntica a la ecuación (45).
Para completar la demostración de nuestro teorema funda­
mental debemos probar que si la segunda máquina también es
reversible, se mantiene el signo de igualdad como se indica en la
ecuación (46).
Si consideramos que la segunda máquina es también reversi­
ble, intercambiando las dos máquinas y aplicando la desigualdad
de la parte (a) de nuestro teorema a las nuevas condiciones ten­
dremos :
Q [ - Q i '
En el presente caso deben cumplirse ésta y la desigualdad
(45), pues hemos supuesto que ambas máquinas son reversibles.
------
36
Pero estas dos desigualdades solo son compatibles si se man­
tiene el signo de igualdad.
El teorema que acabamos de demostrar puede enunciarse
también como sigue:
S i tenemos varias máquinas térmicas, algunas de las cuales
son reversibles, operando en ciclos entre las temperaturas ti y t-j,
las reversibles tendrán todas la m ism a eficiencia, mientras que las
no reversibles tendrán eficiencias que nunca podrán exceder la
eficiencia de las reversibles.
Consideremos en primer lugar dos máquinas reversibles. De
la ecuación (46) y de la definición (44) se deduce inmediata­
mente que sus eficiencias son iguales.
Si tenemos una máquina reversible y otra no reversible, obte­
nemos de la desigualdad (45):
Q ,~
Ql
Por lo tanto,
Q.
«;
Comparando esto con la ecuación (44) vemos que la eficiencia
de la máquina irreversible no puede exceder nunca la de la re­
versible.
El teorema fundamental nos muestra que la relación Qo/Qi
tiene el mismo valor para todas las máquinas reversibles que ope­
ran entre las mismas temperaturas íi y ío; es decir, este cociente es
independiente de las características particulares de la máquina,
siempre que sea reversible; depende solo de las temperaturas ti y
¿2· Podemos por lo tanto escribir:
(5 2 )'
donde f (¿i, Í2) es una función universal de las temperaturas t¡
y ^2·
Demostraremos ahora que la función / {ti, t^) tiene la si­
guiente propiedad:
siendo t^, ti y to tres temperaturas arbitrarias.
.'Í7
;
í
'1
Sean Ai y A 2 dos máquinas cíclicas reversibles que trabajan
entre las temperaturas ío, íi y ío. ti>, respectivamente. Si A i absor­
be a la temperatura íi la cantidad de calor Qi y pierde la cantidad
de calor Qo a la temperatura ío, en el transcurso de un ciclo, entonces, por (52) tenemos :
^ = /(ío, k) .
Vo
Análogamente, si An absorbe la cantidad de calor Q2 a la
temperatura tn y entrega la cantidad Qo a la temperatura Íq (para
mayor simplicidad suponemos que las dos máquinas entregan
iguales cantidades de calor a la temperatura ío) durante cada ci­
clo, será:
! = / ( . , « .
Si dividimos esta ecuación por la precedente, tendremos:
& _ f{U>, fe)
Q i~ / (< o ,íi)·
Consideremos ahora un proceso compuesto en el cual la má­
quina A 2 efectúa un ciclo directo y la -<4i un ciclo inverso. Es obvio
que este proceso será un ciclo reversible, ya que está constituido
por dos ciclos reversibles, separados. Durante el proceso no hay
intercambio de calor a la temperatura ío, porque la cantidad de
calor Qo entregada por la máquina A 2 a la temperatura Íq es reab­
sorbido a esa misma temperatura por la máquina A i operando en
sentido inverso.
Sin embargo, la máquina A 2 absorbe una cantidad de calor
Qo a la temperatura ío y la máquina Aj expele una cantidad de
calor Qi a la temperatura í^ en cada ciclo. Podemos por lo tanto
considerar a Ai y An, cuando trabajan conjuntamente del modo
arriba descrito, como formando una máquina cíclica reversible
que opera entre las temperaturas ti y to. Para esta máqv'.ina será,
por definición de la función f :
I
Comparando esta ecuación con (54), obtenemos (53), como quería­
mos demostrar.
3S
Como la temperatura io considerada en nuestra anterior dis­
cusión es arbitraria, podemos mantenerla constante en todas las
ecuaciones; la función / (ío, i) será en ese caso una función de la
temperatura í solamente, y podremos escribir:
K fik , t) = e{t),
(55)
en donde K es una constante arbitraria.
Utilizando la (55) pondremos la (53) en la siguiente forma:
Esta ecuación nos dice que / (íi, ís) es igual a la relación entre
una función de argumento ío y la misma función de argumento fi.
Como la temperatura í que hemos utilizado es empírica, es
imposible determinar la forma analítica de la función ^ (í). Sin
embargo, dado que nuestra escala de temperaturas es arbitraria,
podemos introducir convenientemente una nueva escala, usando
como temperatura a la función o(t) en lugar de í.
Es de hacer notar, no obstante, que s{t) no está definida en
forma completamente unívoca. De las ecuaciones (56) ó (55)
surge claramente que ®(í) está determinada a menos de un factor
constante arbitrario. Por lo tanto podremos elegir libremente, y
en la forma que consideremos más adecuada, la unidad de la nueva
escala de temperaturas o. La elección de esta unidad se efectúa,
en general, considerando en 100 grados la diferencia entre las tem­
peraturas de ebullición y congelación del agua a una atmósfera
de presión.
La escala de temperaturas que acabamos de definir es la esca­
la absoluta termodinámica de temperatura. Tiene la ventaja de
ser independiente de las propiedades especiales de cualquier sus­
tancia termometrica. Además, utilizando esta escala de tempera­
turas, las leyes de la termodinámica adquieren formas muy simples.
Demostraremos ahora que la temperatura absoluta termodiTiámica © coincide con la temperatura absoluta T, introducida eri el
parágrafo S con la ayuda de un termómetro de gas.
Consideremos un ciclo de Carnot efectuado por un gas i4eal
(para simplificar tomaremos un mol de gas). Sean Ti y T^ las
temperaturas de las dos isotermas del ciclo (medidas con un ter­
mómetro de gas). (Ver fig. 7.) Calculamos en primer lugar la
cantidad de calor Qo absorbida durante la expansión isotérmica AB
a la temperatura Tn. Aplicando la primera ley, ecuación (15), a
la transformación AB e indicando por los subíndices A y B las
magnitudes correspondientes a los estados A y B, tenemos:
39
Ub — Uji -]- Lab “ Qa >
¡
siendo L^ b el trabajo efectuado durante la expansión isotérmica, el
que podemos calcular con la ayuda de la ecuación (10) :
4
I
Lab =
R T 2 lo g
Haremos uso ahora del hecho de que la energía de un gas
ideal es una función de T sx>lamente (ver par. 5). Dado que A y B
están sobre la misma isoterma, deberá ser Ua = Us , de manera que
Q2 =
Lab =
R T i lo g
.
En forma similar podemos demostrar que la cantidad de calor
entregada en la fuente Ti durante la compresión isotérmica re­
presentada por el segmento DC es:
Qi = fíTi log
Ve
Como los puntos
y C se encuentran sobre la misma adiabá­
tica tenemos, por (38);
.T iF r^ =
y del mismo modo,
Dividiendo esta ecuación por la precedente y extrayendo la raíz
(K-1 ), obtenemos:
Va
Ve ·
A partir de ésta y con las expresiones para Q2 y Qi se tiene:
9 i - h
Qi
Tr
Esta ecuación muestra que la relación Q >¡Qi, es igual a la re­
lación Ti/Ty de las temperaturas de las fuentes cuando están ex-
40
presadas en la escala de temperaturas del termómetro de gas. Pero
de (56) se deduce que Q 2 / Q 1 es también igual a la relación de las
temperaturas de las fuentes cuando éstas se expresan en unidades
de la escala absoluta termodinámica. Por consiguiente, la relación
de ambas temperaturas en la escala absoluta termodinámica es
igual a la relación de las mismas en la escala del termómetro de
gas, es decir, que ambas escalas de temperaturas son proporciona­
les. Como las unidades para las mismas se han elegido iguales,
concluimos que las escalas son iguales, es decir, que
e = T.
(57)
Habiendo llegado a esta conclusión, se hace innecesario el
uso de letras distintas para izidicarlas. En adelante, por lo tanto,
utilizaremos T para referirnos a la temperatura absoluta termodi­
námica.
Poniendo T en lugar de ^ tenemos por (56) para un ciclo
reversible entre las temperaturas Ti y T 2 '.
Qa
Ti
j't r o 'j
Q rT iY la expresión para la eficiencia de una máquina reversible toma
la forma
1 _ '^1 _ T t - T\
T.
~ f r -
_
10. Máquinas térmicas
Hemos demostrado ya que ninguna máquina que trabaja entre
dos temperaturas puede tener mayor eficiencia que una máquina
reversible que opera entre esas mismas temperaturas. La ecuación
(59) representa la máxima eficiencia que puede alcanzar una má­
quina entre las temperaturas Ti y Tn.
En la mayoría de las máquinas térmicas la temperatura menor
Ti es la temperatura del medio ambiente, y por lo tanto es incon­
trolable. Es por lo tanto deseable, desde el punto de vista termodinámico, elevar la temperatura T» tanto como sea posible. Por
supuesto, debemos tener siempre presente que la eficiencia real
es en general considerablemente menor que la eficiencia máxima
(59) porque todas las máquinas térmicas están lejos de ser rever­
sibles.
41
Un ciclo de Carnot que se realiza en el sentido inverso puede
ser utilizado para extraer una cantidad de calor Qi de una fuente
a la temperatura menor Ti mediante la absorción de una cantidad
de trabajo L. De las (43) y (58) deducimos fácilmente que
a
=
3
I
i
i
'
Í
(60)
Basados en este principio es posible construir una máquina
refrigeradora utilizando la temperatura ambiente como la tempe­
ratura mayor To . Podríamos así, con rm ciclo de Camot efectuado
en el sentido inverso, extraer el calor Qi de un cuerpo enfriado
hasta una temperatura T¡, menor que la temperatura ambiente,
To. Es evidente, por la ecuación (60), que la cantidad de trabajo
que se requiere para extraer una cantidad de calor Q¡ de un cuerpo
a la temperatura Ti, se hace cada vez mayor a medida que la
temperatura T¡ del cuerpo disminuye.
Como en el caso de una máquina térmica común, la eficiencia
de una máquina refrigerante es considerablemente menor que la
eficiencia termodinámica (60). Esto se debe al hecho de que en
los dispositivos refrigerantes intervienen siempre procesos irre­
versibles.
Problemas
1. Un mol de u n gas m on oatóm ico efectúa un ciclo de Carnot entre las
tem peraturas 400° K y 300® K. En la transform ación isotérm ica superior el
volum en inicial e s de 1 litro y e l final d e 5 litros. H allar el trabajo efectuado
durante ü n ciclo y las can tid ad es de calor intercam biadas con la s d o s fu en tes.
2. ¿Cuál es la m áxim a eficiencia d e un a m áquina térm ica q u e trabaja
entre un a tem peratura superior de 400° C y un a inferior de 18® C?
3. Encontrar la m ínim a cantidad de trabajo qu e se requiere para extraer
una caloría de un cuerpo a — 15° C, cuando la tem peratura del am biente es
de 35® C.
42
CAPITULO IV
LA ENTROPÍA
11. Algunas propiedades de los ciclos
Consideremos un sistema S que sufre una transformación cí­
clica. Supongamos que durante el ciclo el sistema recibe o entrega
calor a un conjunto de fuentes Ti, To, . . . < Tn. Sean Qi, Qa . . Q¡¡>
las cantidades de calor intercambiadas entre el sistema y las fuen­
tes. Tomaremos las Q como positivas cuando representan calor
recibido por el sistema y negativas en caso contrario.
Demostraremos ahora que :
É p á O .
i-1 Ji
(61)
y que el signo de igualdad se cumple si el ciclo es reversible.
Para probar la validez de (61), introducimos, además de las tí
fuentes mencionadas anteriormente, otra fuente de calor a la tem­
peratura arbitraria To, y también n máquinas cíclicas reversibles
(tomaremos n ciclos de Carnot, Ci, Co, . . C„) que trabajan entre
las temperaturas T^, T¿, . . T„, respectivamente, y la tempera­
tura To- El ciclo Ci, que opera entre las temperaturas
y T q, es
tal que entrega la cantidad de calor Qi, a la fuente de temperatura
Ti, es decir, una cantidad igual a la que absorbe el sistema S a la
misma temperatura.
De acuerdo con (58), la cantidad de calor que absorbe C| de
la fuente T q es:
Consideremos ahora un ciclo compuesto, consistente en un
ciclo del sistema S y uno de cada uno de los ciclos de Carnot
C], Co, . . C„. El intercambio neto de calor en cada una de las
43
I,
jj
’j
'1
íj
fuentes Ti, T->, . . .,T ^ durante el ciclo compuesto es cero; la fuente
Ti entrega al sistema S una cantidad de calor Q¡, pero recibe la
misma cantidad de calor del ciclo C¡. La fuente To, por otra parte,
pierde una cantidad de calor igual a la suma de las cantidades (dadas por [62]) que absorben los ciclos de Carnot Ci, C2 , . ■ ·, Ca- La
fuente To entrega entonces en total la cantidad de calor
Oo =
< -l
t-1 i,·
(63)
En consecuencia, el resultado neto de nuestro ciclo compuesto
es que el sistema que constituyen S y Ci, Cn, . . ., Cu recibe de la
fuente T© la cantidad de calor Qq. Pero hemos visto ya que, en una
transformación cíclica, el trabajo efectuado es igual al calor total
recibido por el sistema. Como al final del ciclo compuesto S, Ci,
C2 , .. ., Ca vuelven a su estado inicial, el único resultado que se
obtiene al final de dicho ciclo es transformar en trabajo el calor
recibido de una fuente a la temperatura uniforme Tq. Si Qo fuese
positivo, este resultado estaría en contradicción con el postulado
de Kelvin. Se deduce por consiguiente que Qo í O, por (63),
<-l i ,
que es idéntica a (61)
Si el ciclo que efectúa S es reversible, podremos describirlo
en la dirección opuesta, en cuyo caso todas las Q\ cambiarán de
signo. Aplicando la (61) al ciclo invertido se obtiene:
i-l
i ,
i - l Ti
Si el ciclo es reversible, esta desigualdad y la ecuación (61)
se satisfacen. Esto solo es posible en el caso de que se mantenga el
signo de igualdad. Para un ciclo reversible deberá ser entonces:
tf
t-1 i i
= 0.
Queda así completada la demostración de nuestro teorema,
4
44
(64)
Al fundamentar (61) y (64), hemos supuesto que el sistema
intercambia calor con un número finito de fuentes. Es también
importante considerar el caso en que el intercambio de calor se
efectúa con una distribución continua de fuentes. En tal caso, las
sumatorias en (61) y (64) deben ser sustituidas por integrales que
se extienden sobre todo el ciclo.
Denotaremos por (¿ la integral que se extiende sobre un ciclo
y por dQ la cantidad infinitesimal de calor que el sistema recibe
de una fuente a la temperatura T. Se tiene:
« . . .
(65)
que es válida para todos los ciclos, y
que es válida solo para ciclos reversibles.^
12. La entropía
La propiedad de un ciclo reversible expresada en la ecuación
( 66) puede también formularse de la siguiente forma. Sean A y B
dos estados de equilibrio de un sistema S. Consideremos una trans­
formación reversible que lleva al sistema del estado inicial A al
estado final B. En la mayoría de los casos será posible efectuar
muchas transformaciones entre los estados A y B. Por ejemplo,
si podemos representar el estado del sistema en un diagrama
(V, p ), cualquier curva continua que una los puntos A y B (que
representan los estados inicial y final del sistema ) corresponde a
1
Con el objeto de evitar m alos entendidos en cuanto al significado de
(6 5 ) y (6 6 ), debem os puntualizar que T representa la tem peratura de la
fu en te que entrega la cantidad de calor dQ, que no es necesariam ente igual
a la tem peratura T' del sistem a (o de parte del sistem a) que recibe el calor
dQ. Ciertam ente, si el ciclo es irreversible (relación [ 6 5 ] ) , T ' ^ T cuando dQ
e s p ositiva, ya que el calor no puede fluir del cuerpo m ás frío al más caliente,
y T' ^ r cuand o dQ e s negativa. Cuando el ciclo es reversible (ecuación [ 6 6 ] ) ,
deberem os tener siempre T' — T, porque un intercam bio de calor entre dos
cuerpos a d istin tas tem peraturas no e s reversible. En (66) podem os por lo
ta n to tom ar T com o la tem peratura de la fuente y tam bién la de la parte
del sistem a que recibe el calor dQ.
45
una posible transformación reversible desde A hasta B. En la fi­
gura 9 vemos tres de tales transformaciones.
Fig. 9
Consideremos ahora la integral
que se extiende sobre una transformación reversible desde A hasta
B (dQ es la cantidad de calor que absorbe el sistema en forma
reversible a la temperatura T ) . Demostraremos que esta integral es
la misma para todas las transformaciones reversibles de A a B; es
decir que el valor de la integral para una transformación reversi­
ble depende solo de los estados extremos A y B de la transforma­
ción, y no de la transformación misma.
B
Para demostrar este teorema deberemos probar que si I y II
son dos transformaciones reversibles entre los estados extremos
A y B (en la fig. 10 los estados están representados por puntos y
las transformaciones por líneas como ayuda visual para la prue­
ba). Tenemos entonces:
( 67 )
46
donde hemos tomado las integrales a lo largo de los caminos
I y n, respectivamente.
Analizaremos la transformación cíclica A I B II ¿4, Se trata
de un ciclo reversible por estar constituido por dos transforma­
ciones reversibles. Podemos aplicar aquí la ecuación (66), de mo­
do que
Jl Aal]B l l A
'^e = o.
T
Esta integral puede descomponerse en la suma de dos integrales:
La segunda integral de esta expresión es igual a — ( I
^ )
T /ii’
porque en la transformación de B a
a lo largo del camino II,
dQ toma los mismos valores, con signo opuesto, que en la trans­
formación de A a B a \o largo de II. Obtenemos así la ecuación
(67) y queda demostrado nuestro teorema.
La propiedad que se expresa por medio de la ecuación (67)
nos permite definir una nueva función del estado de un sistema,
la entropía. Esta función, que es de suma importancia en la ter­
modinámica, se define de la siguiente manera.
Elegimos en forma arbitraria un cierto estado de equilibrio
de nuestro sistema y lo llamamos estado de referencia. Sea A
cualquier otro estado de equilibrio, y consideremos la integral
sJ'i
tomada a lo largo de una transformación reversible. Hemos visto
ya que una integral de estas características depende solo de los
estados extremos O y
y no de una transformación reversible
particular entre O y A. Sin embargo, como ya hemos fijado el
estado de referencia O, podremos decir que (68) es una función
del estado A únicamente. Denominaremos a esta función la en­
tropía del estado A.^
2
La necesidad de restringir esta definición de entropía solam ente a los
estados de equilibrio, surge del hecho de que la transform ación entre O y A
debe ser reversible: es decir, debe ser un a sucesión de esta d os de equilibrio.
Por consideraciones de continuidad se deduce que tam bién los esta d os inicial
y final O y A deben ser estados de equilibrio.
47
j·
'i
Gansideremos ahora dos estados de equilibrio Á y B, y sean
S ( A ) y S (B ) las entropías de esos estados, respectivamente. De­
mostraremos que
!
S(B) - S(A ) =
^
!
i[
dQ
(69)
7”
donde la integral se toma sobre una transformación reversible
entre los estados A y B.
Para probar esto debemos tener en cuenta que la integi;ál
sobre la derecha en (69) tiene el mismo valor para todas’ las
transformaciones reversibles entre A y B. Podemos, por lo tanto,
elegir una transformación particular que consiste en dos transfor­
maciones reversibles, la primera desde A hasta el estado de refe­
rencia O y la segunda desde O hasta B. Podemos escribir entonces
la integral en (69) como la suma de dos integrales:
r
í -
Í T
+
l ’ f-
Por la definición ( 68) se tiene:
puesto que la transformación entre O y B es reversible. Se tiene,
además:
Substituyendo estos dos valores en las integrales del segundo
miembro de (70) obtenemos (69), como queríamos demostrar.
En m uchos casos, sin embargo, e s posible definir la entropía para e sta ­
dos que n o son estados de equilibrio. Tom emos, por ejem plo, u n sistem a
com puesto por varias partes h om ogéneas a diferentes tem peraturas y presio­
nes. Su pon gam os que cada un a de esas partes tien e presión y tem peratura
uniform es. Si las diversas partes del sistem a están en contacto directo unas
con otras, es evid en te que el sistem a n o estará en equilibrio, y a que el calor
fluirá de la s partes m ás calientes a la s m ás frías y las diferencias de presión
darán lugar al m ovim iento. Si, en cambio, encerram os cada parte en un
recipiente rígido y térm icam ente aislado, nuestro sistem a estará en equilibrio
y estarem os en condiciones de determ inar su entropía.
48
La definición (68) de entropía requiere la elección arbitraría
de un estado de referencia O. Podemos demostrar fácilmente que,
si en lugar de O, elegimos un estado de referencia distinto O',
el nuevo valor, S '{A ), que encontramos para la entropía del esta­
do A, difiere del primitivo, S ( A ) , solo en una constante aditiva.
Si tomamos O' como el nuevo estado de referencia, tenemos
por definición:
S'(A )
'U Q
T>
donde la integral se extiende sobre una transformación reversible
desde O' hasta A. Aplicando la (69) a esta integral encontra­
mos que
S '(^ ) = S(A) - s m ,
o también
S{A) - S 'iA ) = 5(0').
(71)
Como el nuevo estado de referencia O' es fijo, S(O ') es una cons­
tante (es decir, es independiente del estado variable A ) . Así,
la (71) nos muestra que la diferencia entre las entropías del es­
tado A obtenidas mediante dos estados de referencia distintos,
O y O', es una constante.
La entropía queda entonces definida a menos de una cons­
tante aditiva. Esta indeterminación no será un obstáculo, siempre
que operemos con diferencias de entropías. En algunos problemas,
sin embargo, la constante aditiva de la entropía juega un papel
muy importante. Veremos más adelante cómo la tercera ley de la
termodinámica completa la definición de entropía y nos permite
determinar la constante de entropía (ver cap. V III).
Si consideramos una transformación infinitesimal reversible,
durante la cual la entropía varía en dS y el sistema recibe una
cantidad de calor dQ a la temperatura T, se deduce de (68) y
(69) que
dS =
(72)
Es decir, que la variación en entropía durante una transformación
infinitesimal reversible se obtiene dividiendo la cantidad de calor
absorbido por el sistema por la temperatura del sistema.
La entropía de un sistema compuesto por varias partes es
generalmente igual a la suma de las entropías de cada una de
49
ellas. Esto se cumple si la energía del sistema es la suma de las
energías de cada una de sus partes y el trabajo realizado por el
sistema durante la transformación es igual a la suma de las cantidades de trabajo efectuado por todas las partes que lo componen,
Hacemos notar que estas condiciones no son obvias y que en algunos casos pueden no cumplirse. Por ejemplo, en el caso de un
sistema compuesto por dos substancias homogéneas, sería posible
expresar la energía como la suma de las energías de ambas solo si
la energía de las superficies de contacto entre ambas fuera despre­
ciable. Esta energía de superficie se puede despreciar general­
mente en los casos en que las dos substancias no están muy
finamente subdivididas; de lo contrario puede tener una impor­
tancia muy considerable.
Supongamos, para mayor simplicidad, que nuestro sistema S
está constituido solamente por dos sistemas parciales Si y S 2 , y que
la energía Í7 de S es igual a la suma de las energías Ui y U2 de
¡,
!.
í
i'
i
>;
;
Si y S 2 '.
t7 = l7 i-f Ua;
supongamos también que el trabajo L que efectúa el sistema S
durante una transformación es igual a la suma de Li y L 2 , esto
es, a la suma del trabajo realizado por Si y Sn, respectivamente:
li =
L i - j - Z/2 ·
De estas hipótesis y de (15) surge que el calor Q que recibe
el sistema S durante una transformación puede escribirse como
la suma,
Q
=
Q l +
Q a,
de las cantidades de calor recibidas por cada una de las partes
componentes. Esto nos permite descomponer la integral (68 ), que
determina la entropía, en la suma:
de dos integrales que definen la entropía de los dos sistemas par­
ciales Si y S2.®
3
Debem os hacer n otar qu e si el estado de referencia O y el estado A
son conocidos, tam bién lo son los correspondientes estados de las dos partes
que com ponen el sistem a total. E stos esta d o s de lo s dos sistem as parciales
h a n sido indicados con las m ism a s letras O y A.
1
-
50
Cuando se cumplen las condiciones para su validez, esta aditividad de la entropía nos permite en varios casos determinar la
entropía de un sistema aun cuando éste no se encuentre en estado
de equilibrio. Esto es posible si logramos subdividir el sistema en
un número de partes de modo que cada una d.e ellas esté en equi­
librio. Podremos entonces determinar la entropía de cada una de
ellas y, por definición, tomar la entropía de todo el sistema como
igual a la suma de las entropías de sus partes componentes.^
13. Otras propiedades de la entropía
Consideremos dos estados i4 y B de un sistema. Por (69) te­
nemos :
S(B) - S (^)
-
Ja
T'
siempre que tomemos la integral sobre una transformación rever­
sible de A a B. Si la integral se toma sobre una transformación
irreversible de ^ a B la ecuación precedente no se cumple. Demos­
traremos que, en tal caso, obtenemos la desigualdad
‘ TO
Para lograrlo, llevamos nuestro sistema del estado A al estado
B a lo largo de una transformación irreversible, I, y volvemos
nuevamente a A a lo largo de una transformación reversible, R
(ver fig. 11). Obtenemos así un ciclo reversible A l B R A. Si
aplicamos la (65) a este ciclo tenemos;
- /
AIBSÁ
f - ( j : 9 h
{ í : n
·
* P uede dem ostrarse fácilm ente que tod a s las propiedades y a atribuidas
a la entropía, se aplican tam bién a esta definición generalizada.
51
Como la (69) puede aplicarse a ía transformación reversible, 22,
desde B hasta Ay se tiene:
t
Substituyendo ésta en la desigualdad precedente se llega a:
- [5 (B) - 5 (A)],
O^
de modo que, para el caso general de cualquier tipo de transfor­
mación de A a B, será
l
‘ ^
s S(B) - S M ),
y ésta es una expresión idéntica a (73), como queríamos de­
mostrar.
Para un sistema completamente aislado, (73) adopta una for­
ma muy simple. Dado que para tal sistema dQ = O, encontra­
mos que :
S iB )^ S (A )·,
(74)
es decir, que, para cualquier transformación que se efectúa en un
sistema aislado, la entropía del estado final no puede ser nunca
menor que la del estado inicial. Si la transformación es reversible,
se mantiene en (74) el signo de igualdad y la entropía del sistema
no se modifica.
Debe quedar bien claro que el resultado de (74) se aplica
únicamente a sistemas aislados. Así es que, con la ayuda de un
sistema externo, es posible reducir la entropía de un cuerpo. La
entropía de ambos sistemas tomados en conjunto, en cambio, no
puede disminuir.
Cuando un sistema aislado se halla en estado de máxima en­
tropía compatible con su energía, no puede sufrir ningún otro
cambio, ya que cualquier transformación ocasionaría una disminu­
ción de la entropía. Siendo así, el estado más estable para u n sis­
tema aislado es el estado de m áxim a entropía. Podemos ilustrar
mediante dos ejemplos simples el hecho de que todas las transfor­
maciones espontáneas en un sistema aislado tienen lugar en la
dirección del aumento de la entropía.
52
Como primer ejemplo consideremos el intercambio de calor
por conducción térmica entre dos partes, Ai y Ao, de un sistema.
Sean Ti y Tn las temperaturas de esas partes, respectivamente, y
Tx < T2. Dado que el calor fluye por conducción del cuerpo más
caliente al más frío, el cuerpo Ao entrega una cantidad de calor Q
que es absorbida por A i . La entropía de Ai cambia entonces en la
cantidad Q/Ti, mientras que la de A>¡ cambia en la cantidad
— Q/T2. La variación de entropía de todo el sistema es :
Q__Q .
Ti
Ti
Es obvio que esta variación es positiva, ya que Ti < Tn, y por lo
tanto la entropía de todo el sistema se ha incrementado.
Como segundo ejemplo, tomemos la producción de calor por
fricción. Este proceso irreversible da también como resultado un
aumento en la entropía. La parte del sistema que es calentada por
fricción recibe una cantidad positiva de calor y su entropía crece.
Como el calor no proviene del sistema, sino que se obtiene por
medio del trabajo, este aumento de entropía no es compensado por
una disminución en ninguna otra parte del mismo.
El hecho de que la entropía de un sistema aislado no puede
disminuir durante una transformación cualquiera tiene una inter­
pretación muy clara desde el punto de vista estadístico. Boitz­
mann ha demostrado que la entropía de un estado dado de un
sistema termodinàmico está relacionada en forma muy simple con
la probabilidad de dicho estado.
Hemos ya subrayado la diferencia entre los conceptos diná­
micos y termodinámicos del estado de un sistema. Para deter­
minar el estado dinámico es necesario conocer en detalle la posición
y el movimiento de todas las moléculas que componen el sistema.
El estado termodinàmico, en cambio, queda determinado dando
solo un pequeño número de parámetros tales como temperatura,
presión, etc. De aquí se deduce, por lo tanto, que a cada estado
termodinàmico corresponde un gran número de estados dinámicos.
En mecánica estadística se usan criterios para asignar a un estado
termodinàmico dado el número tt de estados dinámicos correspon­
dientes. (Ver también par. 30). Este número tt recibe el nombre
de probabilidad del estado termodinàmico dado, aunque en sen­
tido estricto es solo proporcional a la probabilidad en el sentido
habitual. Esta última se obtiene dividiendo tt por el número total
de estados dinámicos posibles.
En concordancia con consideraciones estadísticas, supondre­
mos ahora que en un sistema aislado se producen solo aquellas
transformaciones espontáneas que lo llevan a estados de mayor
probabilidad, de modo que el estado más estable de tal sistema
será el de máxima probabilidad compatible con la energía total
del mismo.
Vemos que esta hipótesis establece un paralelismo entre las
propiedades de la probabilidad tt y la entropía S de nuestro siste­
ma, y sugiere así la existencia de una relación funcional entre
ambas. Esta relación fue establecida realmente por Boitzmann,
quien demostró que
S=3fclog7T,
(75)
donde k es una constante denominada constante de Boitzmann y
es igual a la relación,
(76)
A’
entre la constante de los gases, R, y el número de Avogadro, A.
Sin hacer una comprobación de (75), podemos demostrar,
suponiendo que existe una relación funcional entre S y “n·,
S=
/ ( 7 t ) ,
(77)
que la entropía es proporcional al logaritmo de la probabilidad.
Consideremos un sistema compuesto de dos partes, y sean
S i y S 2 las entropías y tti y it2 las probabilidades de los estados de
ambas. Por (77) tenemos;
Si = /(7ri);
S2 = f(iT2)·
Pero la entropía de todo el sistema es la suma de las dos en­
tropías:
S = Si + S2;
y la probabilidad de todo el sistema es el producto de las dos pro­
babilidades,
7T =
7T1 7 T 2 .
De estas ecuaciones y de (77) obtenemos:
/(tTI TTs) = /(tTi) + /(7T2) .
La función f, por consiguiente, debe satisfacer la ecuación
funcional :
54
f( x y ) ^ f^ x ) + i(y ).
(78)
Esta propiedad de / nos permite determinar su forma. Dado que
(78) se cumple para todos los valores áe x e y, podemos tomar
y = 1 -f· ®, donde * es un infinitésimo de primer orden. Entonces,
/ ( x + x s ) - / ( x ) + / ( l + e).
Desarrollando ambos miembros por el teorema de Taylor y des­
preciando todos los términos de orden mayor que el primero, te­
nemos:
/ (x) + * * / ' ( » ) - / ( x ) + / ( 1) + e / '(l).
Para £ *= O, resulta / (l) — 0. Por lo tanto,
x / '( x ) - / '( l ) - f c ,
donde k representa una constante, o:
X
Integrando, obtenemos:
/(x) -= fc log X + const.
Recordando (77), tenemos finalmente:
S — k log 7T+ const.
Podemos hacer la constante de integración igual a cero. Esto es
permisible porque la entropía está determinada a menos de una
constante aditiva. De este modo hemos obtenido (75).
Debe entenderse claramente, por supuesto, que esto no consti­
tuye una prueba de la ecuación de Boltzmann (75), puesto que no
hemos demostrado que exista una relación funcional entre S y ir;
solo hemos indicado, la plausibilidad de dicha relación.
14. La entropía de sistemas cuyos estados pueden ser representa­
dos en un diagrama (V, p)
El estado de estos sistemas queda determinado por dos cua­
lesquiera de las tres variables, p, V, T. Si elegimos T y V como
variables independientes (variables de estado), el calor dQ que
55
recibe el sistema durante una transformación infinitesimal, como
resultado de la cual T y V varían en dT y dV, está dado por la
expresión diferencial (22)
(79)
De ésta y (72) obtenemos:
dS
T
T\dT)v
’^
t
X
óV / t
'^^.
dV.
(80)
Estas dos expresiones diferenciales de dQ y dS difieren en
dos aspectos muy importantes. Conocemos, por la teoría general,
que existe una función S del estado del sistema. En nuestro caso,
S será por lo tanto una función de las variables T y V, que deter­
minan el estado del sistema:
S = S(T, V).
(81)
La expresión del segundo miembro de (80) es entonces la
diferencial de una función de las dos variables independientes
T y V.
En general, se dice que una expresión diferencial de dos va­
riables independientes x e y, tal como:
dz = M{x, y)dx
N{x, y)dy,
(82)
es una diferencial exacta, si es la diferencial de una función de
X e y. Podemos decir, por consiguiente, que (80) es una diferencial
exacta de las variables independientes T y V.
Es bien sabido que si dz es una diferencial exacta, M y N
deben satisfacer la siguiente ecuación:
dMjx, y) ^ dNjx, y)
dy
dx
(83)
Cuando esta condición se cumple, es posible integrar (82) y encon­
trar así una función que satisfaga dicha ecuación. Si la condi­
ción no se cumple, la función no existe, y dz no puede considerarse
como diferencial de una función de x e y; entonces, la integral
de (82) a lo largo de un camino que une dos puntos sobre el plano
L
56
{x, y) depende no solo de dichos puntos (límites de la integral),
sino también del camino que los une.
Fig. 12
En cuanto a las dos expresiones diferenciales (79) y (80),
hemos visto ya que dS es una diferencial exacta. Si consideramos
en el diagrama (V, p) dos estados A y B conectados por dos trans­
formaciones reversibles diferentes, I y II (ver fig. 12), e integramos
dS a lolargo de los dos caminos I y II, obtenemosen ambos casos
el mismoresultado, es decir, S(B ) = iS (A ). Si, por otra parte,
integramos dQ a lo largo de esos caminos, obtenemos dos resul­
tados, Ql y Q2, que en general no son iguales. Esto puede veri­
ficarse fácilmente si aplicamos la primera ley de la termodinámica
(15), a las transformaciones I y n. Encontramos así que:
Qj. = U{B) - U(A) + Li
QiT = U(B) - U{A) + L n .
Restando ambas expresiones, obtenemos:
Ql --- Qll =
Li --- Lji .
Lii están dados por las áreas AIBB'A'A y AllBB'A'A, respec­
tivamente, Como la diferencia entre estas dos áreas es igual al área
i4IBIM, se deduce que Li — Ln y, por tanto, Qi — Qu son, en ge­
neral, distintos de cero. En ese caso, (79) no es una diferencial
exacta, y no podemos encontrar una función Q del estado del sis­
tema. Debemos hacer notar que si realmente existiese un fluido
calórico, como se había supuesto antes del desarrollo de la ter­
modinámica moderna, se podría hallar una función Q del estado
del sistema.
Examinemos, como ejemplo de las consideraciones preceden­
tes, las expresiones dQ y dS para un mol de un gas ideal. De (30)
tenemos:
dQ — CvdT -j- pdV,
57
o, eliminando p con la ayuda de la ecuación de estado pV = RT,
I
I
li:
dQ ^C vdT + ^ d V .
(84)
,
4i
Í
Esta expresión no es una diferencial exacta, y se puede verificar
de inmediato que la condición (83) no se cumple.
De (84) y (72) se tiene:
=
‘
= ^ á T + ^dV .
(85)
En este caso la condición (83) se cumple; por lo tanto esta expre­
sión es una diferencial exacta.
Integrando (85), obtenemos:
S = C y lo g T + R l o g V + a,
i
(86)
donde a es una constante de integración. Esta constante aditiva
permanece indeterminada de acuerdo con la definición (68) de
la entropía. (Ver, no obstante, el par. 32.)
Podemos transformar la expresión (86) para la entropía de un
mol de un gas ideal, tomando, en lugar de V, su valor V = J2T/p
que obtenemos de la ecuación de estado. Teniendo en cuenta (33),
obtenemos:
<S = Cp log r — fí log p + a +
log R.
(87)
Volviendo al caso general de cualquier substancia cuyo estado
se puede determinar por las variables T y V, se obtiene la expre­
sión (80) para la diferencial de entropía. La condición (83) apli­
cada a esta expresión nos da:
9 ( l d U \ _
d V '\ T d T j
(d J J
Y
dT I T V9 7
vJ,
9
f l
en la cual hemos omitido los subíndices V y T porque en todas estas
fórmulas usaremos a V y T como variables independientes. Si
efectuamos las derivaciones parciales indicadas en la ecuación
precedente y agrupamos términos, obtenemos el importante re­
sultado:
L
58
Aplicaremos la (88) para demostrar que la energía U de una
substancia que satisface a la ecuación de estado pV = UT es fun­
ción de la temperatura únicamente y no depende del volumen. Ya
hemos visto que esto fue verificado experimentalmente por Joule;
sin embargo, es interesante lograr este resultado como una conse­
cuencia directa de la ecuación de estado.
Substituyendo la expresión p = R T /V en (88 ) encontramos
que:
\dV jT
d T \ V
J
RT
= 0,
la cual demuestra que U es independiente de V.
Si elegimos como variables independientes T, p o p, V en lugar
de T, V, obtenemos otras dos ecuaciones que son substancial­
mente equivalentes a (88). Siendo así, si tomamos T y p como
variables de estado, dQ estará dada por (23). Como dS => dQ/T
es una diferencial exacta, podemos tener fácilmente, con la ayuda
de (83):
En forma similar, tomando p y V como las variables independien­
tes, obtenemos de (24) y (83):
15. La ecuación de Clapeyron
En este parágrafo aplicaremos la ecuación (88 ) a un vapor
saturado, es decir, a un sistema compuesto por un líquido y su
vapor en equilibrio.
Consideremos un líquido encerrado en un cilindro que tiene
un émbolo en un extremo. El espacio entre la superficie del lí­
quido y la de contacto del émbolo estará lleno de vapor saturado
5
N ó tese que e ste resultado n o es com pletam ente independiente del
experim ento de Joule descrito en el paràgrafo 5. En efecto, la prueba de la
identidad entre la tem peratura T del term óm etro de gas y la tem peratura
term odinám ica & que dim os en el parágrafo 9 estuvo basada en los resultados
del experim en to de Joule.
59
a la presión p, que solo depende de la temperatura del vapor y
no de su volumen.
Las isotermas para este sistema líquido-vapor en un diagra­
ma (V ,p ) se obtienen como sigue. Manteniendo la temperatura
constante, incrementamos el volumen del vapor desplazando el
émbolo hacia afuera. Como resultado de esto, y para mantener
invariable la presión de vapor, parte del líquido se evaporará. De
este modo, mientras quede en el cilindro suficiente líquido, un
aumento de volumen del sistema no modifica la presión de vapor.
Por lo tanto, la isoterma por una mezcla de un líquido y su vapor
en equilibrio es una curva de presión constante, y, por consi­
guiente, paralela al eje V, como puede observarse en la región
comprendida por la línea de puntos de la figura 13.
Cuando el aumento de volumen haya llegado a un grado tal
que todo el líquido se haya transformado en vapor, un incremento
posterior del mismo dará como resultado, como puede verse en la
figura 13, que la presión disminuya, tal como sucede en el caso
de un gas.
Si ahora comprimimos nuestro sistema, manteniendo todavía
la temperatura constante, la presión aumentará hasta igualar la
del vapor saturado correspondiente a dicha temperatura. En este
punto, una disminución en el volumen no producirá un aumento
de la presión. Lo que sucede, en cambio, es que una parte del
vapor se condensa, y la presión permanece invariable (trecho hori­
zontal de la isoterma).
Cuando el volumen na sido reducido a tal punto que la subs­
tancia se encuentra completamente en estado líquido, una com­
presión posterior produce un gran aumento en la presión; esto
se debe a la muy baja compresibilidad de los líquidos. En este
60
tramo, la pendiente de la isoterma será muy pronunciada, como
lo muestra la figura.
En la figura 13 se han dibujado algunas isotermas del tipo de
las que acabamos de mencionar, para distintos valores de la tem­
peratura (curvas a, b, c, d). Podemos ver en la figura que la
longitud del tramo horizontal de la isoterma (es decir, el inter­
valo de volumen en el cual pueden coexistir el líquido y el vapor
en equilibrio a una temperatura dada) decrece a medida que
aumenta la temperatura, hasta que para la isoterma ee, su lon­
gitud se reduce a un infinitésimo (es decir, a un punto de infle­
xión horizontal). La isoterma ee es lá llamada isoterma crítica,
y su temperatura Te es la temperatura crítica. El volumen Ve y
la presión Pc, que corresponden al punto de inflexión horizontal,
se denominan volumen crítico y presión crítica·, el estado corres­
pondiente a Ve, Pc y Te es el llamado estado crítico (o punto crí­
tico) del sistema.
Las isotermas para las temperaturas por encima de la tem­
peratura crítica son funciones monótonas decrecientes que no tie­
nen discontinuidades. Para temperaturas muy altas se convierten
en hipérbolas equiláteras, porque las propiedades de la substancia
en el rango de las temperaturas muy elevadas se asemejan cada
vez más a las de un gas ideal.
La línea de puntos y la isoterma crítica ee de la figura divi­
den el plano (V,p) en cuatro secciones: la indicada con L, que
corresponde al estado líquido; la indicada con L, V, correspon­
diente a la mezcla de líquido y vapor saturado; la sección V, que
corresponde al vapor no saturado y la sección G, correspondiente
al gas.
Aplicaremos ahora (88) al sistema líquido-vapor representado
en la figura 13 por la región L, V, del plano {V, p ) . En esta región
la presión y las densidades del líquido y el vapor dependen úni­
camente de la temperatura. Sean Vj y v^ los volúmenes específicos
(es decir, los volúmenes por unidad de masa, o sea la inversa de las
densidades) del líquido y el vapor, respectivamente; y sean Ui y
sus energías específicas (energía por unidad de masa). Las can­
tidades p, vu v-j, U\ y U2 son todas funciones de la temperatura'
solamente. Si m es la masa total de la substancia, y m\ y mn son
las masas de las partes de líquido y vapor, respectivamente, en­
tonces
m = 771] -|- Too .
Del mismo modo, el volumen y la energía total del sistema son
V = m iV i(T ) + m^VníT)
U = miUi(T)
mju-j(T) .
61
i-
Consideramos ahora una transformación isotérmica de nuestro
sistema, que da como resultado el pasaje de una cantidad dm de
substancia del estado líquido al estada vapor, y que produce una
variación dV en el volumen total y una variación dU de la energía
total del sistema. Al final de la transformación tendremos en­
tonces (toi — dm) gramos de líquido y (m3 -f" dm) gramos de
vapor, de manera que el volumen total será igual a:
V + dV = ( m i — d m )viiT ) + (m2 + dm) Vo(T)
^ V + { v , ( T ) — v^i T) }dm,
dV = {vn (T) — Vi ( T ) ) dm.
(91)
Del mismo modo, la energía total variará en una cantidad
dU = {U2ÍT) — U i(T )} dm.
(92)
Por la primera ley, ecuación (21), se tiene:
y
d Q ^ d U + pdV
= dm{ut — Wi -f- p(»s — tfi)},
o también
^
am
= U i - ui + p(vt - vO = X.
( 93 )
La ecuación (93) es la expresión de la cantidad de calor
necesaria para vaporizar un gramo de líquido a temperatura cons­
tante; esto es lo que denominamos calor latente de vaporización,
A. Su valor es distinto para diferentes líquidos y depende también
de la temperatura. Para el agua a la teniperatura de ebullición
y a la presión normal es X = 540 cal/g.
Dado que (91) y (92) se refieren a transformaciones isotér­
micas, la relación dUJdV nos da:
u,(T) - u,{T)
o, utilizando (93)
62
Si comparamos a esta ecuación con la ( 88) y escribimos dp/dT en
íd p \
\d T /y
lugar de ( — J , ya que para nuestro sistema la presión es función de la temperatura T únicamente, vemos que:
^
^____.
dT
(94)
T{v2-v0
Ésta es la ecuación de Clapeyron.
(3omo un ejemplo de aplicación de la ecuación de Clapeyron,
calcularemos la relación dp/dT para el vapor de agua a la tem­
peratura de ebullición y a la presión normal. Tenemos:
Xc= 540 cal/g = 2260
V2 = 1677;
X
lO"^ erg/g
Vi = 1,043
;
T = 373,1.
Substituyendo estos valores en (94), obtenemos:
dp
----- = 3,62
dT
X
10^ dina/cm^ grado = 2,7 cm.Hg/grado.
Un valor aproximado para dp/dT se obtiene de la ecuación de Cla­
peyron suponiendo que Vi es despreciable con respecto a Vo, y
calculando, luego Vn admitiendo que el vapor satisface la ecuación
de estado de un gas ideal.
Para un gramo de vapor, se tiene, por la ecuación (6 ):
m = ^T ,
(95)
siendo M el peso molecular del vapor. La ecuación (94) se con­
vierte en:
dp _ \ M
dT
RT^^’
^ ^
dT
^
RT^’
-
Para el vapor de agua a la temperatura de ebullición, esta
fórmula da d p/dT = 3,56 X 10*; ésta es una muy buena aproxi­
mación al valor 3,62 X 10* que se oíatiene mediante cálculos
exactos,
63
Considerando el calor de vaporización A como constante en
un amplio intervalo de temperaturas, podemos integrar (97) y
obtener;
,
AM
log p ------------ + constante ,
.
4
^
RT
o
p = constante, e »*·
(98)
Esta fórmula muestra en forma aproximada cómo la presión
de vapor depende de la temperatura.
Hemos obtenido la ecuación de CHapeyron para un sistema
líquido-vapor, pero podemos aplicar la misma fórmula a cualquier
cambio de estado de una substancia. Como ejemplo, la aplicare­
mos a la fusión de un sólido. Un sólido sometido a una presión
dada funde a una temperatura exactamente determinada, que
varía con la presión que se le aplica. Por consiguiente, para un
sistema sólido-líquido, la presión para la cual ambos estados pue­
den coexistir es función de la temperatura. Usaremos (94) para
calcular la derivada de esta función. Las cantidades A, Vi y V2
representan en este caso el calor de fusión y los volúmenes espe­
cíficos del sólido y el líquido, respectivamente.
Si tomamos como ejemplo la fusión del hielo, tenemos:
X = 80 cal/g = 335 X IQ·^ erg/g, v, =1,0907 cm®/gm, Vn =
= 1,00013 cmVgm, T = 273,1. Substituyendo estos valores en
(94) obtenemos:
dT
■i <
= — 1,35 X 10® dina/cm- grado =■ — 134 atm/grado.
Esto exr>resa que un incrrmento de 134 atmósferas hace disminuir
en 1° el punto de fusión del hielo.
Debemos hacer notar, en particular, que el punto de fusión del
hielo disminuye con el aumento de la presión. A este respecto, el
agua tiene un comportamiento distinto al de la mayoría de las
substancias. En casi todos los casos, el punto de fusión aumenta
con el aumento de la presión. Este comportamiento irregular del
agua se debe a que el hielo es menos denso que ella, mientras que
en la mayoría de los casos el sólido es más denso que el líquido.
El hecho de que el punto de fusión del hielo disminuya me­
diante el aumento de la presión es de considerable importancia en
geofísica, ya que este fenómeno es el responsable del movimiento
de los glaciares. Cuando la masa de hielo encuentra una roca
en el lecho del glaciar, la gran presión de aquél contra la roca hace
64
bajar su punto de fusión en esa zona y ocasiona la fusión del
hielo sobre un lado de la roca. El congelamiento se produce
inmediatamente después de suprimida la presión. De esta manera
la masa de hielo puede deslizarse muy lentamente, sorteando
obstáculos.
16. La ecuación de van der Waals
Para altas temperaturas y presiones, la ecuación caracterís­
tica de un gas ideal representa con bastante aproximación el
comportamiento de los gases reales. Sin embargo, cuando la tem­
peratura y la presión son tales que el gas se halla cerca del punto
de condensación, se observan importantes desviaciones de las
leyes de los gases ideales.
Entre las numerosas ecuaciones de estado que se han introdu­
cido para representar el comportamiento de los gases reales, la de
van der Waals es especialmente interesante por su simplicidad y
la forma satisfactoria en que describe el comportamiento de mu­
chas substancias en un amplio intervalo de temperaturas y pre­
siones.
Van der Waals dedujo su ecuación de consideraciones basadas
en la teoría cinética, tomando en cuenta como primera aproxi­
mación el tamaño de una molécula y las fuerzas de cohesión entre
moléculas. Su ecuación de estado (para un mol de substancia) es:
(p + a/y2) iV — b) = R T ,
(99)
en la cual a y b son constantes características para una substancia
dada. Cuando a = b = 0 , la (99) se reduce a la ecuación carac­
terística de un gas ideal. El término b representa el efecto que
se origina en el tamaño finito de las moléculas, y el término a/V^
corresponde al efecto de las fuerzas de cohesión molecular.
En la figura 14 se han dibujado algunas isotermas calculadas
a partir de la ecuación de estado de van der Waals. Si las com­
paramos con las isotermas de la figura 13, vemos que poseen
muchas características similares. En ambos casos encontramos
una isoterma que tiene un punto de inflexión horizontal C. Es
la isoterma crítica, y el punto de inflexión es el punto crítico. Las
isotermas por encima de la temperatura crítica muestran en am­
bas figuras un comportamiento similar. Sin embargo, se observan
diferencias en las isotermas por debajo de la temperatura crítica.
Las de van der Waals son curvas continuas con un mínimo y un
máximo, mientras que las de la figura 13 tienen dos puntos angu­
lares y son horizontales en la región en la cual las isotermas de
65
r
14;
van der Waals tienen su máximo y mínimo. La razón de la dife­
rencia cualitativa en el comportamiento de los dos conjuntos de
isotermas en la región señalada como L, V en la figura 13 es que
los puntos del tramo horizontal de las isotermas en esa figura no
corresponden a estados homogéneos, ya que, a lo largo de ese
tramo, la substancia se divide en una parte líquida y una de vapor.
Ì-
'i
pi
t
I'l/'
W'l
Fig. 14
-4
■i
|:
Si comprimimos isotérmicamente un vapor no saturado, hasta
alcanzar la presión de saturación, y luego reducimos aún más el
volumen, generalmente se produce la condensación de una parte
del vapor sin un nuevo incremento de la presión. Esto corresponde
a las isotermas de la figura 13. No obstante, si comprimimos el
vapor muy cuidadosa y lentamente, y lo mantenemos libre de
partículas de polvo, podremos alcanzar una presión considerable­
mente mayor que la de saturación, sin llegar a la condensación.
En esta situación decimos que el vapor está sobresaturado. Pero
los estados sobresaturados son lábiles; cualquier leve alteración
puede producir la condensación, haciendo que el sistema pase a
un estado estable caracterizado por una fase líquida y una de
vapor.
Los estados lábiles son muy importantes para nuestro plan­
teo, porque ilustran la posibilidad de existencia de estados homo­
géneos en la región del vapor saturado. Suponemos que esos
estados’ lábiles están representados por el tramo BCDEF de la iso­
terma de van der Waals ABCDEFG (fig. 15), mientras que el
tramo horizontal BF de la isotei-ma discontinua ABHDIFG repre­
senta los estados estables líquido-vapor'. Si fuese posible realizar
todos los estados lábiles que están sobre la isoterma de van der
Waals, podríamos pasar, mediante un proceso isotérmico conti-
66
nuo, del estado vapor, representado por el tramo FG de la iso­
terma, al de liquido, representado por el tramo BA.
Dada una isoterma de van der Waals, puede ser necesario
determinar cuál es la presión de vapor saturado cuando su tem­
peratura es igual a la de la isoterma, o geométricamente hablando,
a qué altura por encima del eje V debemos dibujar el tramo hori­
zontal BF que corresponde al estado líquido-vapor. Demostrare­
mos que esta distancia debe ser tal que las áreas BCDH y DIFE
sean iguales.
En primer lugar, debemos probar que el trabajo efectuado
por un sistema durante un ciclo isotérmico reversible es siempre
cero. Por (16) vemos que el trabajo efectuado durante un ciclo
es igual al calor absorbido por el sistema. Pero, para un ciclo
reversible, se cumple la ( 66), y como en nuestro caso el ciclo es
isotérmico, podemos sacar 1 /T fuera del signo integral en (66).
La ecuación ( 66) expresa ahora que el calor total absorbido, y por
consiguiente el trabajo total realizado durante el ciclo, es cero.
Fig. 15
Consideraremos ahora el ciclo
isotérmico
reversible
BCDEFIDHB (fig. 15). El trabajo efectuado durante el ciclo, me­
dido por el área, debe ser nulo. Pero mientras DEFID, descrita en
el sentido de .las agujas del reloj, nos da un área positiva, BCDHB^
descrita en sentido contrario, tiene un área negativa. Dado que el
área total del ciclo BCDEFIDHB es cero, los valores absolutos de
las áreas de los ciclos BCDHB y DEFID deben ser iguales. Esto es
lo que justamente queríamos probar.
La demostración anterior podría objetarse basándose en que,
como es obvio, el área del ciclo isotérmico BCDHB no se anula,
y por lo tanto, no es cierto que el trabajo efectuado durante un
ciclo isotérmico reversible es siempre cero. La respuesta a esta
objeción es que el ciclo BCDHB no es reversible.
Para comprobarlo debemos hacer notar que el punto D repre-
67
senta en nuestro diagrama dos estados diferentes, según lo consi­
deremos como un punto perteneciente a la isoterma de van der
Waals o como un punto de la isoterma líquido-vapor BHDIF. Aun­
que el volumen y la presión representados por D son los mismos
en ambos casos, en el caso de la isoterma de van der Waals D
representa un estado homogéneo lábil, mientras que en el caso
de la isoterma líquido-vapor D representa un estado estable no
homogéneo compuesto por una fase líquida y una fase vapor. Al
efectuar el ciclo BCDHB, pasamos del estado D, sobre la isoterma
de van der Waals, al estado D sobre la isoterma líquido-vapor.
Como este último estado es más estable que el estado D sobre la
isoterma de van der Waals, egte pasaje es irreversible, ya que no
podría producirse espontáneamente en la dirección opuesta. Es así
que todo el ciclo BCDHB es irreversible, y por lo tanto su área no
se anula.
Los datos del estado crítico T^., Ve y Pc de una substancia
pueden ser expresados en términos de las constantes a. y b de la
substancia, que aparecen en la ecuación de van der Waals.
Cuando p y T se conocen, la ecuación de van der Waals (99)
es una ecuación de tercer grado en V. Hay entonces, por lo gene­
ral, tres raíces distintas de V para valores dados de T y p. La iso­
terma crítica, T — T e , tiene, sin embargo, un punto horizontal
de inflexión en p = Pe, V = Ve', es decir, que hay un contacto de
tercer orden en
Ve entre la isoterma crítica y la línea horizon­
tal p = Pe. De aquí se deduce que la ecuación cúbica en V, que se
obtiene poniendo p = Pe y T = Te en (99) tiene la raíz triple
V — Vc. Esta ecuación cúbica puede escribirse así:
VcV^ — (Pcb + RTe) V- + aV — ab = 0 .
a
■;
Como Ve es una raíz triple de esta ecuación, el primer miembro
debe ser de la forma Pe(V — Vf)^ . En consecuencia, tendremos
por comparación que:
Vi =
Pc
3Vl = - ;
Pc
y
3K =
Pc
Resolviendo estas tres ecuaciones para Ve, Pc y T^ obtenemos
las ecuaciones;
y
( 100.
que expresan los datos críticos en términos de las constantes
a y b.
68
Es interesante hacer notar que si tomamos Pe, Ve y Te como
las unidades de
volumen,presión y temperatura, respectivamente,
la ecuación de van der Waals adopta la misma forma para todas
las substanciéis. Poniendo
9 = L·
Ve
^ = —
T;
Ό = Χ·
Fe'
y haciendo uso de (100), obtenemos de (99):
( ^ + | ) ( · ο - | ) = |^ .
(101,
Como esta ecuación contiene solo constantes numéricas, es la mis­
ma para todas las substancias. Los estados de varias substancias,
determinados por los mismos valores de P, V y T son los llamados
estados correspondÁentes, y la ( 101) es frecuentemente denomi­
nada “ ecuación de van de Waals de los estados correspondientes” .
En el parágrafo 14 hemos demostrado que si una substancia
cumple la ecuación de estado pV = RT, de un gas ideal, podemos
deducir termodinàmicamente que su energía depende solo de la
temperatura y no del volumen. Esto es cierto solo para gases idea­
les. Para gases reales, U depende también del volumen. De (99)
deducimos que;
ésta y la (88) dan:
(
d V jr
dT \V -b
V^-j
V -b ^V ^
_ a
- Y2Si integramos esta ecuación con respecto a V (manteniendo T
constante), obtenemos:
U = -^+ f(T ),
(103)
pues la constante de integración debe ser constante con respecto
a V solamente, pero puede, por lo tanto, ser una función de T.
69
a
^
El termino------ en ^103), representa la energia potencial de las
fé
fuerzas de cohesión entre las moléculas.
No podemos determinar f ( T ) utilizando únicamente medios
termodinámicos; su determinación requiere algunos datos sobre
calores específicos. Supongamos, por ejemplo, que el calor molecular a volumen constante, C„, es constante. De (25) y (103) se
obtiene entonces:
^
l· ^
^
'
u!
^,
,
Integrando, se tiene:
f{T) = CvT + w,
donde tu es una constante. La ecuación (103) es ahora:
V = CvT - ^ + w.
(104)
Con esta expresión de la energía podemos calcular fácilmente
la entropía de un mol de un gas de van der Waals. De (72), (21),
(102) y (104) obtenemos:
= 1 m
ds = ^
+ pdv)
r
T ^ " F - 6’
e integrando
S = Cylog T + R log (F - 6) + const.
(105)
Obsérvese la similitud de esta fórmula con la (86 ), que es la
expresión para la entropía de un gas ideal.
En el parágrafo 6 hemos definido una transformación adia­
bática como una transformación reversible durante la cual el siste­
ma está térmicamente aislado. A lo largo de una transformación
adiabática será entonces dQ = 0 , de manera que, por (72),
1
70
dS = djQ/T = 0, o bien S = constante. Así es que, si un sistema
sufre una transformación adiabática, su entropia permanece cons­
tante. Por esta razón es que a veces se las denomina también
isoentrópicas..
La ecuación de una transformación adiabática de un gas de
van der Waals se obtiene de inmediato a partir de (105), haciendo
constante la entropía. Esto da:
Cr \og T + R log (F — 6) = const.
T{V - b y = const.
(106)
Esta expresión para las adiabáticas de un gas de van der Waals es
muy similar a la ecuación (38) para las de un gas ideal.
Problemas
1. ¿Cuál e s la variación de entropía de 1.000· gram os de agua cuando
se los lleva desd e la tem peratura de congelam iento a la de ebullición? (Supo­
ner un calor específico co n sta n te = 1 c a l / g grado.)
2. Un cuerpo cum ple la ecuación de estado:
p 7 1 ,2 = 109 r i . l
Una m edición de su capacidad térm ica dentro de un recipiente que tien e un
volum en con stan te de 100 litros, m uestra que bajo esas condiciones la capa­
cidad térm ica es con stan te e igual a 0,1 ca l/g ra d o . Expresar la energía y la
entropía del sistem a com o una función de T y V.
3. El punto de ebullición del alcohol etílico (CsHoO) es de 78,3® C; el
calor de vaporización e s de 855 jouV gram o. Hallar d p / d T en el punto de
ebullición.
71
CAPITULO V
^14·.1
POTENCIALES TERMODINÁMICOS
Hi
17. La energía libre
(’
if :
En un sistema puramente mecánico, el trabajo externo L
que se efectúa durante una transformación es igual a menos la va­
riación, AU , de su energía. Es decir:
L = — At; .
(107)
Para los sistemas termodinámicos no existe una relación tan sim­
ple entre el trabajo realizado y la variación de energía, ya que
puede haber intercambio de energía en forma de calor entre el
sistema y el medio circundante. Tenemos, en lugar de ello, la
primera ley de la termodinámica (15), que podemos escribir en
la forma:
L = — AU + Q.
_
jí
I
.|í
i-f
5,
En sistemas termodinámicos, muchas de las transformaciones se producen mientras éstos se hallan en contacto térmico con
el medio ambiente, lo que da lugar a un intercambio de calor
entre el sistema y el medio que lo circunda. En ese caso, L puede
ser mayor o menor que — AU, dependiendo esto de que el siste­
ma absorba o entregue calor al medio ambiente.
Supongamos ahora que nuestro sistema S está en contacto
térmico con un medio ambiente a la temperatura constante T, y
consideremos una transformación del mismo desde un estado
inicial A hasta un estado final B. Si aplicamos la desigualdad (73)
a esta transformación, tenemos:
>
S(B) - S(A).
â-
(108)
72
Como el sistema solo recibe calor de una fuente cuya temperatura
es constante, podemos sacar 1 /T fuera del signo integral, y encon­
tramos que
Q =
T{S(B) - S(A)}.
(109)
Obtenemos así un límite superior para la cantidad de calor que el
sistema puede recibir del medio que lo circunda. Si la transfor­
mación de A a B es reversible, el signo de igualdad se mantiene
en (73) y por lo tanto también en (109). En este caso (109)
da exactamente la cantidad de calor que el sistema recibe du­
rante la transformación.
De (108) y (109) tenemos, poniendo a U = U(B) — U(A) :
L ^ ' U ( A ) — U(B)
4-T[S(B)
— SU)] .
(110)
Esta desigualdad fija un límite superior para la cantidad de
trabajo que puede obtenerse durante la transformación de A a B.
Si la transformación es reversible se mantiene el signo de igual­
dad, y en ese caso, el trabajo efectuado es igual al límite superior.
Supongamos ahora que las temperaturas de los estados inicial
y final A y B, son las mismas e iguales a la temperatura T del
medio ambiente. Definimos una función F del estado del sistema
como sigue :
F = U — TS
(111)
Podemos ahora escribir (110) en términos de esta función F, que
es la llamada energía libre del sistema :
L ¿ F ( A ) — F (B ) = — AF.
(112)
En (112) también se mantiene el signo de igualdad si la transfor­
mación es reversible.
El contenido de la ecuación (112) puede expresarse así:
Si un sistema sufre una transformación reversible desde un
estado inicial A hasta un estado final B, siendo la temperatura gn
ambos estados igual a la del medio ambiente, y si durante la trans­
formación el sistema intercambia calor solo con el medio ambiente,
el trabajo que el mismo efectúa durante la transformación es
igual a la disminución de la energía libre del sistema. Si la trans­
formación es irreversible, el decremento de la energía libre del
sistema es solo un límite superior del trabajo realizado por el
mismo.^
Este resultado s e expresa con frecuencia de la siguiente manera:
Cuando un sistem a sufre un a transform ación isotérm ica, el trabajo L
73
íi
I*
’i
^
la
il ,
Comparando (112) con (107), la cual se cumple solamente
para sistemas puramente mecánicos, vemos que, en sistemas termodinámicos capaces de intercambiar calor con el medio circundante,
la energía libre juega un rol análogo al de la energía en los sistemas mecánicos. La diferencia fundamental consiste en que, en
(107), el signo de igualdad se mantiene siempre, mientras que
en (112), solo se conserva para las transformaciones reversibles.
Consideramos ahora un sistema que se encuentra aislado diná­
micamente (no térmicamente) del medio que lo circunda. Esto
significa que cualquier intercambio de energía en forma de tra­
bajo entre el sistema y el medio es imposible. El sistema puede
efectuar únicamente transformaciones isocoras.
Cuando el sistema se halla encerrado en un recipiente de
volumen invariable, si la presión en cualquier instante es la misma
para todas las partes del sistema, y éste solo realiza trabajo como
efecto de las fuerzas que ejerce la presión sobre las paredes del
recipiente que lo contiene, dicho sistema está dinámicamente ais­
lado. De otro modo, la aislación dinámica requeriría métodos más
complicados.
Aunque nuestro sistema está dinámicamente aislado, súpo­
nemos que se halla en contacto térmico con el medio ambiente y
que su temperatura es igual a la temperatura T del medio. Para
cualquier transformación del sistema, tenemos L -= 0; obtenemos
entonces de (112) :
O s F ( A ) — F(B),
o
F(B)íF(A).
( 113 )
Es decir, si el sistema está en contacto térmico con el medio a la
temperatura T, y si está dinámicamente aislado de modo que
no puede efectuar ni absorber trabajo externo, su energía libre no
puede aumentar en el transcurso de una transformación.
Como consecuencia de este hecho tenemos que, si la energía
libre es u n mínimo, el sistema se halla en equilibrio estable; esto
es así porque cualquier transformación produciría un incremento
en la energía libre, lo cual estaría en contradicción con (113).
En,el caso de sistemas mecánicos, existe equilibrio estable cuando
qüe realiza, nunca puede superar la variación
(con signo cam biado) d e su
energía libre; si la transform ación es reversible, L es igual a —
N uestro resultado e s m á s general porque se cum ple no solo para tr a n s­
form aciones isotérm icas, sino tam bién para aquéllas durante la s d ia le s el sis­
tem a alcanza tem peraturas d istin ta s de T en los estados intermedios, con tal
que el intercam bio de calor se efectú e solam ente con el m edio am biente que
se halla a una m ism a tem peratura T en todos sus puntos·
74
la energía potencial es mínima. Dado que la condición para el
equilibrio estable de un sistema termodinàmico contenido en un
recipiente rígido y a la temperatura del medio ambiente es que la
energía libre sea un mínimo, ésta es frecuentemente denominada
el “ potencial termodinàmico a volumen constante” . Hacemos notar,
sin embargo, que, en lenguaje riguroso, la condición para la vali­
dez de (113) no es solo que el volumen del recipiente sea constante
sino también que el sistema no efectúé ningún trabajo extemo. Si
la presión que actúa sobre el sistema es uniforme, entonces las
dos condiciones son equivalentes.
Consideremos ahora una transformación isotérmica, I, de un
sistema a la temperatura T desde un estado
a un estado B, y
también una transformación isotérmica, II, entre los estados A ‘
y B' a la temperatura T -f- áT. A ' se obtiene a partir de A por
medio de una transformación infinitesimal durante la cual la
temperatura se eleva en dT mientras no se efectúa ningún tra­
bajo externo. Si el sistema está sometido en su totalidad a una
presión uniforme, esto puede efectuarse si los volúmenes de A
y A' son iguales (transformación isocora). Análogamente, durante
la transformación de B a B', el sistema no debe realizar trabajo.
Sean L y L + dL las cantidades máximas de trabajo que pue­
den obtenerse de las transformaciones I y II, respectivamente. Te­
nemos entonces
L = F{A) - F(B)
(114)
L + dL = F (A ’) - F{B'),
dL
dT
dF(A)
dT
dF{B)
dT ’
(115)
donde dF{A) y dF{B) representan, respectivamente, a ^ (^ 0 —
— F(A) y F(B') — F (B ). Pero tenemos:
F (A ) = C7 (A) — TS(A),
o bien, diferenciando,
d F { A ) ^ d V { A ) ~ T d S i A ) — dTS{A ).
(116)
Como durante la transformación desde A hasta A' no se efec­
túa ningún trabajo, la cantidad de calor que recibe el sistema en
el transcurso de la transformación infinitesimal es, de acuerdo
con (15),
75
d Q A ^dÜ (A );
.
I .
y, por (72),
t '
.S U )
=
La ecuación (116) da ahora:
dF(A)
dT ~
F(A)
- ~T~
U{A)
T ·
Análogamente, obtenemos:
dF{B)
dT ~
F{B)
~ T
U{B)
T '
De (114) y (115) se tiene así:
L - r g
= -A U ,
(117)
donde Aü = U(B) — U (A ) es la variación de energía que resulta
de la transformación desde A hasta B. La ecuación (117) es
la llamada isocora de van’t Hoff y tiene numerosas aplicaciones
útiles.
A esta altura, vamos a deducir una expresión útil para la
presión de un sistema cuyo estado puede ser representado en un
diagrama (V, p ) . Consideremos una transformación infinitesimal
isotérmica y reversible que hace variar el volumen del sistema
en una cantidad dV. Podemos aplicar a esta transformación la
ecuación ( 112) con el signo de igualdad, ya que se trata de una
transformación reversible. Dado que:
L = pdV.
tenemos, por ( 112),
76
y
( a
(118)
· - ·
Concluiremos este parágrafo dando la expresión para la ener­
gía libre de un mol de un gas ideal. Esto se logra inmediatamente
a partir de las ecuaciones (111), (29) y ( 86 ) :
í ’ = Cvr + W ^ T ( C v l o g r + R l o g V + a ).
(119)
Si utilizamos (87) en lugar de (86), obtenemos la fórmula equi­
valente:
F =. CyT + W — T (Cp log r — ñ log p + a + ñ log R ) . (120)
18. Eli potencial termodinàmico a presión constante
En muchas transformaciones termodinámicas la presión y la
temperatura del sistema no cambian, sino que permanecen iguales
a la presión y temperatura del medio circundante en el transcurso
de la transformación. En tales circunstancias es posible definir
una función $ del estado del sistema que tiene la siguienteipropiedad. Si la función ^ es un mínimo para valores dados de la presión
y temperatura, entonces el sistema estará en equilibrio a la pre­
sión y temperatura dadas.
Consideremos una transformación isotérmica e isobàrica a la
temperatura constante T y .a la presión constante p, que lleva a
nuestro sistema desde un estado vi a un estado B. Si V(i4) y
V (B) son los volúmenes inicial y final que ocupa el sistema, enton­
ces el trabajo realizado durante la transformación es:
L ^ p [ V i B ) — V(A)].
Dado que la transformación es isotérmica, podemos aplicar
la ecuación ( 112); haciéndolo así obtenemos:
p V (B ) — p V ( A ) ^ F i A ) — F(B).
Definimos ahora una nueva función $ del estado del sistema co­
mo sigue:
^ = F + pV = U ~ T S
pV.
(121)
En términos de 4·, la precedente desigualdad se convierte en:
$ ( B ) í 4 .(A ).
(122)
77
jj
¡I
']
Ì':
st
ií.
La función ^ es el potencial termodinàmico a presión cons~
tante. De (122) se deduce que, en una transformación isobàrica e
isotérmica de un sistema, el potencial termodinàmico a presión
constante nunca puede aumentar.
Podemos decir, por lo tanto, que si la temperatura y la pre­
sión de un sistema se mantienen constantes, el estado del sistema
para el cual el potencial termodinàmico ^ es un mínimo, es un
estado de equilibrio estable. La razón para ello es que si $ es un
mínimo, cualquier cambio espontáneo en el estado del sistema
tendría el efecto de incrementar 4>; pero esto estaría en contradic­
ción con la desigualdad ( 122).
Son algunas veces útiles las siguientes propiedades de $ para
sistemas cuyos estados pueden ser representados sobre un dia­
grama ( V , p ) .
Si elegimos T y p como variables independientes y diferencia­
mos (121) con respecto a p, tendremos que:
Pero por la definición de entropía y por la primera ley tenemos
para una transformación reversible;
dQ = TdS = dU + pdV;
o, en nuestro caso, para un cambio isotérmico de presión :
K a-(s).«(a·
1^·:
En consecuencia, vemos que:
(123)
\dp/r
Análogamente, diferenciando (121) con respecto a T, podemos
demostrar que;
(124)
Como ejemplo de la utilidad del potencial
lo emplearemos
para obtener la ecuación de Clapeyron, que ya hemos deducido
en el parágrafo 15 empleando un método diferente.
78
Consideremos un sistema compuesto por un líquido y su vapor
saturado, encerrados dentro de un cilindro y mantenidos a presión
y temperatura constantes. Si Vi, U^, Sy, S^, y
V 2 son las ener­
gías, entropías y volúmenes de las partes líquido y vapor, respec­
tivamente, y 17, S' y V las correspondientes cantidades para el sis­
tema total, entonces,
Í7 =. í/j + Ü2
S = Si
V=
Sa
+ Vo,
de modo que, por ( 121),
donde
y $2 son los potenciales de las partes líquido y vapor,
respectivamente.
Sean ttij y tus las masas de líquido y vapor respectivamente, y
sean Ui, si, V\ y ipi, y M2, S2,
y v>2 las energías específicas, entro­
pías, volúmenes, y potenciales termodinámicos del líquido y el
vapor. Tenemos entonces:
= ■wii
$ 0
=
771 o ^ 2
·
Sabemos, por las propiedades generales de los vapores satu­
rados, que todas las cantidades específicas Ui, Uo, s¡, S2 , Vi y Vn,
y la presión p son funciones de la temperatura solamente. Por lo
tanto <pi y <fs son funciones de T únicamente, y podemos escribir:
^ = TIli tpi (T) -|- ^ 2 V>2 ( T ) .
Partiendo del sistema en equilibrio efectuamos una transfor­
mación isotérmica a presión constante de modo que solo mi y mo
pueden variar. Supongamos que, como resultado de la transforma­
ción, Ttiy se incrementa en dmx. Entonces, como mi + rtio = m =
= const., mo disminuye en una cantidad dmi. El potencial termodinámico estará dado ahora por la expresión;
( tu i + d m i )
- f (wi2 — d m i ) y^2 = $ +
d m i (<pi —
92 ) ·
Como el sistema se hallaba inicialmente en estado de equili­
brio, ^ debió haber sido un mínimo en el momento inicial. De
79
W '
M'
esto y de la ecuación anterior se deduce que
li:
^
il ·
<PX
<P2,
o bien
'
:F'. ■
I?f ‘
(Wo-- Ui) --- T (S2--- Si) + P (Vn -- Vi) = 0.
Derivando con respecto a T, vemos que;:
iì
I'
iilíi - uO — T ~ ( s 2 — Si) — («2 — ’ l)
Pero
dT
dT^^dT'
En consecuencia, la precedente ecuación se reduce a:
-(s2 - 5i) + ^ ( t » j - Vi) = 0.
Pero (so — Si) es la variación de entropia cuando un gramo
de liquido se vaporiza a temperatura constante; por lo tanto, es
igual a V!T, donde A es el calor de vaporización de la substancia.
Obtenemos así la ecuación de Clapeyron;
¡
y
i
dp _
dT
T{v2 - i^i) ·
Escribiremos ahora la expresión del potencial termodinàmico
a presión constante para un mol de gas ideal. De (121), (120), la
ecuación de estado, p V = RT, y (33), obtenemos:
Ii. = C,T’ + W — T (C, log r — ñ log P - f a + ñ lo g ñ ).
(125).
i
I
19. La regia de las fases
I
Cuando un sistema està constituido por solo una substancia
homogénea, se dice que consta de una sola fase. Si cada una de las
partes que constituyen un sistema heterogéneo, considerada aisla80
damente, es homogénea, se dice que el número de fases del sistema
es igual al número de partes homogéneas que contiene.
Como ejemplo de un sistema compuesto por una sola fase
podemos considerar un líquido homogéneo (no necesariamente \ina
substancia químicamente pura; también podemos considerar solu­
ciones), un sólido homogéneo o un gas.
Los que damos a continuación son ejemplos de sistemas que
consisten en dos fases: un sistema compuesto de agua y vapor de
agua; una solución saturada de una sal en agua con presencia
de una parte sólida de dicha sal; un sistema compuesto por dos
líquidos inmiscibles, etc. En el primer ejemplo las dos fases son:
una fase líquida compuesta por agua y una fase gaseosa compuesta
de vapor de agua. En el segundo, las dos fases son: la solución de
sal en agua y la sal sólida. En el tercero las dos fases son dos
líquidos.
Todas las propiedades específicas de una fase (es decir, las
propiedades referidas a la unidad de masa de la substancia que
constituye la fase, por ejemplo: la densidad, el calor específico,
etc.) dependen de la temperatura T, la presión p y la constitu­
ción química de la fase.
Para determinar la constitución química de una fase debe­
mos dar el porcentaje de cada substancia químicamente definida
presente en dicha fase.
Más exactamente, podríamos plantear que si se conociera el
porcentaje de cada elemento químico (incluyendo la cantidad
total del elemento, tanto libre como ligado químicamente a otros
elementos), el porcentaje de los diferentes compuestos que se po­
drían formar con los elementos dados estaría determinado por la
temperatura T y la presión p de la fase. Efectivamente, conoce­
mos por las leyes de la química que, dada cualquier temperatura,
presión y concentraciones relativas de los varios elementos pre­
sentes, siempre se puede alcanzar el equilibrio químico dentro de
la fase. Podemos, por lo tanto, decir que una fase es una mezcla
homogénea de todos los posibles compuestos químicos que pueden
formarse a partir de los elementos químicos presentes en la fase,
y que el porcentaje de cada compuesto presente está completa­
mente determinado por T, p y las concentraciones relativas de
todos los elementos de la fase.
(Consideremos, por ejemplo, una fase gaseosa que consiste
en dos concentraciones definidas de hidrógeno y oxígeno a una
presión y temperatura dadas. Las moléculas más numerosas que
se forman con el hidrógeno y el oxígeno serán Ha, O2 y H2O (para
simplificar hemos despreciado las moléculas más raras, H, O, O3
y H2O0). El número de moléculas de agua que se formarán en
nuestra mezcla gaseosa, a una temperatura y presión dadas, está
81
;
!
'
li
/j ; ^
unívocamente determinado, y por lo tanto también lo está la constitución de la mezcla gaseosa, por las concentraciones del hidrógeno y del oxígeno exclusivamente. De manera más estricta, po­
demos decir que los componentes independientes de una fase son
los elementos químicos que ésta contiene (cada elemento debe
considerarse como un componente independiente mientras esté
presente en su forma elemental o en combinación química con
otros elementos). Sin embargo, por consideraciones químicas, se
sabe que, bajo ciertas condiciones, muchos estados de equilibrio
químico se logran solo después de un período excesivamente largo,
comparado con los intervalos de tiempo comunes. Si, por ejemplo
tenemos una mezcla gaseosa de H2 y O2 a temperatura y presión
normales, el equilibrio químico se alcanza cuando una gran can­
tidad del hidrógeno y el oxígeno se combinan para formar va­
por de agua. Pero la reacción
2 Ha + O2 = 2 H2 O
i
se efectúa en condiciones normales con tanta lentitud que, prác­
ticamente, en un período corto no se produce ninguna combina­
ción de hidrógeno y oxígeno. Por supuesto que la reacción se
efectuaría mucho más rápidamente si la temperatura fuese sufi­
cientemente elevada o si contáramos con un catalizador adecuado.
De la exposición precedente surge que, en todos los casos
en los cuales tenemos un compuesto químico que se forma o se
disocia con excesiva lentitud, podemos considerar al compuesto
mismo (y no los elementos que lo constituyen prácticamente) co­
mo un componente de la fase. Por ejemplo, si tenemos una fase
gaseosa consistente en hidrógeno, oxígeno y vapor de agua a
temperatura tan baja que prácticamente no se produce ni for­
mación ni disociación del agua, diremos que nuestra fase contiene
los tres componentes independientes O2, H2 y H2O (y no sola­
mente los componentes hidrógeno y oxígeno) ; la constitución quí­
mica de la fase está entonces determinada por las masas de Oo,
Hj y H2 O por unidad de masa de la fase.
Surge claramente de estas consideraciones que el número de
componentes independientes puede ser mayor o menor que el
número total de elementos químicos presentes. En el ejemplo
anterior teníamos tres componentes independientes (H2, O2, H2 O)
en lugar de dos (H y O). Por otra parte, si solo tenemos vapor
de agua, podremos despreciar su disociación en hidrógeno y oxíge­
no y considerar que la fase está constituida por un solo com­
ponente, el agua.
Consideremos ahora un sistema compuesto de f fases y de n
componentes independientes. Sea mi}¡ la masa de la /c-ésima com-
82
ponente presente en la i-ésima fase. La distribución de las com­
ponentes entre las varias fases puede entonces ser conveniente­
mente descrita por el ordenamiento:
W
il ,
7 7 Í2 1 ,
* · ·
f W
Í7 Í1 2 ,
»122 ,
■ · ·
, W /I
min,m2n,
/i
, mfn .
A una temperatura y presión dadas, la condición de equili­
brio de nuestro sistema es que el potencial termodinàmico $ sea
un mínimo. Esta condición da lugar a un conjunto de relaciones
entre las cantidades de (126).
Supondremos que la energía de superficie de nuestro sistema
es despreciable, de modo que podremos igualar $ a la suma de los
potenciales termodinámicos de todas las fases:
$ = $1 + $ 2 + . . . +
(127)
La función
depende de T, p, y de las masas m u , m i 2 , . .
m¡n de los varios componentes en la i-ésima fase:
% = *1 {T, p, m u, . .
mi„).
(128)
La forma de esta función depende de las propiedades par­
ticulares de la í-ésima fase. Hacemos notar, sin embargo, que *i,
considerada como una función de las n variables m u , mtz, . . .
min, es homogénea de primer grado. En efecto, si hacemos variar
m u , m i 2 , . . . » Wj„, en un mismo factor K, no alteramos la cons­
titución de nuestra fase (puesto que ésta depende solo de las re­
laciones entre las m ) , pero la masa total se incrementa en el
factor K. De este modo,
se multiplica también por él mis­
mo factor K.
Para que nuestro sistema se halle en equilibrio a una deter­
minada temperatura y presión, $ debe ser un mínimo. Analíti­
camente, esto significa que si sometemos a nuestro sistema a una
transformación infinitesimal a temperatura y presión constantes,
la variación resultante en ^ debe ser nula. Supongamos una trans­
formación como resultado de la cual se transfiere una cantidad
8m (que debemos considerar como un infinitésimo de primer or­
den) del fc-ésimo componente, de la í-ésima a la j-ésima fase, sin
que se produzcan cambios en todos los otros componentes y fases.
Entonces, muc se convierte en 7»¡k — Sm, y m;* en
+ Sm. En
83
cuanto a la variación de
solo
así la condición de mínimo:
54> =
y
dm,t
«;
-^ =
érriik
cambiarán. Obtenemos
Sm —
drriik
Sm = O,
( 129)
dnijk
Como debe existir para cada dos fases cualesquiera y para
cualquiera de los componentes·, una ecuación similar, obtenemos
el conjunto de las n (/ — 1 ) ecuaciones de equilibrio:
dmn
d^2
dnhi
dTJlii
d<t>2
drua
dmin
d^2
drruin
3<I>i
í.:
di>f
Orri/i
_
34>/
dm/2
d^f
dm/n
(130)
Estas ecuaciones solo dependen de la constitución química de
cada fase y no de la cantidad total de substancia presente en la
fase. En efecto, como (128) es una función homogénea de primer
grado eñ las m, su derivada con respecto a cualquiera de las m
será homogénea de cero grado; es decir, su derivada depende sola­
mente de los cocientes entre tmíi, '^»2, ■· · » Wi«. En la ordenación
(126) vemos que existen (n — 1 ) j tales cocientes (los n — 1 co­
cientes de las variables contenidas en una columna [126] deter­
minan la constitución de una fase). Además de estas (n — 1) /
variables, tenemos también las variables T y p en (130). Conta­
mos así, en total, con 2
(n — 1 ) / variables.
La diferencia, v, entre este número y el número n (/ — 1)
de las ecuaciones (130) es el número de las (n — 1) / + 2 va­
riables que pueden ser elegidas arbitrariamente, quedando las
variables restantes determinadas por las ecuaciones (130). De­
nominaremos a V, grado de varianda o número de grados de liber­
tad del sistema. Tendremos:
V = (n - 1)/ + 2 - (/ - l)n,
íi
¿
°
(131)
V = 2 + n - /.
84
Esta ecuación, que fue deducida por Gibbs, expresa la regla
de las fases. Nos dice que un sistema compuesto de / fases y n
componentes independientes tiene una variancia v = 2 -{-n —-f.
Por “ variancia” se entiende el número de variables (tomamos
como tales a T, p y las variables que determinan la constitución
de todas las fases) que pueden ser elegidas arbitrariamente.
Para evitar confusiones, advertimos que se considera sola·
mente la composición y no la cantidad total de cada fase, porque
el equilibrio termodinàmico entre dos fases solo depende de la
constitución y no de la cantidad total presente de las dos fases,
como lo demuestra (129). Algunos ejemplos ilustrarán la forma de
aplicación de la regla de las fases.
Ejemplo 1. Sistema compuesto por un fluido homogéneo quí­
micamente definido. Tenemos aquí una sola fase (/ = 1) y \in
componente (n = l ) . De (131) obtenemos entonces v = 2 . Pode­
mos, entonces, elegir las dos variables T y p, arbitrariamente;
pero no tenemos ninguna otra posibilidad de variar la constitución,
ya que nuestra substancia es un compuesto químicamente defini­
do. (Nótese que la cantidad total de substancia, como ya lo hemos
establecido, no se cuenta como un grado de libertad.)
Ejemplo 2. Sistema homogéneo compuesto por dos gases quí­
micamente definidos. Tenemos aquí una fase (/==1) y dos com­
ponentes independientes (n = 2). De (131) surge que v = 3. En
efecto, podemos elegir libremente T, p y la relación de las dos
componentes que determina la composición de la mezcla.
Ejemplo 3. Agua en equilibrio con su vapor saturado. En este
caso tenemos dos fases, líquido y vapor, y solo un componente, de
modo que f = 2 y n ~ l . Tenemos entonces u = 1. Solo podemos
elegir arbitrariamente la temperatura, y la presión será entonces
igual a la presión del vapor saturado para la temperatura dada.
Como solo hay un componente, es obvio que no tenemos libertad de
elección en la composición de las dos fases. También en este ejem­
plo hacemos notar que para una temperatura dada podemos tener
equilibrio entre cantidades arbitrarias de agua y vapor de agua,
siempre que la presión sea igual a la presión de saturación. No
obstante, las cantidades de agua y vapor de agua no se consideran
como grados de libertad.
Ejemplo Jf. Sistema constituido por un compuesto químico en
tres fases diferentes: sólido, líquido y vapor, como, por ejemplo,
hielo, agua y vapor de agua. Tenemos aquí un componente y tres
fases: n = 1, / = 3. Por (131) tenemos entonces que v ~ 0. Esto
85
\l
•t '
iI ■
ì·
significa que no hay libertad de elegir ninguna variable; las tres
fases pueden coexistir solo para un valor fijo de la temperatura
y la presión.
Esto puede ser ilustrado con la ayuda del diagrama de la figu­
ra 16, en el cual las temperaturas y presiones están representadas
como abscisas y ordenadas, respectivamente.
il
il
La curva AB representa la presión del vapor de agua saturado
en función de la temperatura. Cuando los valores de T y p corres­
ponden a un punto sobre la curva, el agua y el vapor de agua
coexisten. Si incrementamos la presión manteniendo constante la
temperatura, el equilibrio entre el agua y el vapor de agua deja de
existir, y toda la substancia se condensa en la fase líquida. Si, por el
contrario, dibítiinuimos la presión, toda la substancia se evapora.
Por consiguiente, para puntos por encima de la curva A B tenemos
agua, y por debajo de dicha curva tenemos vapor, como lo indica la
figura.
La curva AC es análoga a AB, pero corresponde a la presión
del vapor saturado en contacto con hielo y no con agua líquida.
Por encima de la curva AC el hielo es estable, y por debajo lo
es el vapor.
Dado que el agua y el vapor pueden coexistir a lo largo de
AB y el hielo y el vapor pueden coexistir a lo largo de AC, es
necesario que el punto correspondiente, en el diagrama, a los va­
lores de T y p para los cuales hielo, agua y vapor coexisten, esté
sobre ambas curvas; dicho punto coincide con el de intersección,
A, de las dos curvas. Vemos, entonces, que las tres fases pueden
coexistir únicamente para un valor determinado de la tempera·
tura y la presión.
El punto A se denomina punto triple porque es la intersec­
ción, no solo de la curva agua-vapor y de la curva hielo-vapor,
86
sino también de la curva hielo-agua AD. Estas tres curvas dividen
el plano T, p en tres regiones que representan las zonas de esta­
bilidad de vapor, hielo y agua; el punto triple se encuentra en el
límite de las tres regiones.
El punto triple del agua se halla a T = 0,0075“ C y p =
0,00602 atm. Como la presión en el punto triple es menor que
la presión atmosférica, la línea horizontal p = 1 atm. (línea de
puntos en el diagrama) intercepta las tres regiones hielo, líquido
y vapor. La intersección de la línea de puntos con la curva AD
corresponde a una temperatura igual a la del punto de congelación
f del agua a la presión atmosférica (a 0“ C). Lr. intersección b
con la curva AB corresponde a la temperatura de ebullición del
agua a la presión atmosférica (100“ C).
Para algunas substancias la presión en el punto triple es
mayor que una atmósfera. Para dichas substancias, la línea pun­
teada horizontal, que corresponde a la presión atmosférica, está
por debajo del punto triple y en consecuencia pasa de la región
correspondiente al sólido a la de vapor sin interceptar la que co­
rresponde al líquido. A la presión atmosférica estas substancias
no se licúan, sino que pasan directamente de la fase sólida a vapor
(sublimación); pueden existir en la fase líquida solo a presiones
suficientemente elevadas.
20. Termodinámica de la celda electrolítica reversible
En todas las aplicaciones previas de las leyes de la termo­
dinámica hemos considerado generalmente sistemas que podían
efectuar únicamente trabajo mecánico. Sin embargo, como ya
hemos visto en el parágrafo 3, el trabajo mecánico y el'eléctrico
obedecen a las mismas leyes termodinámicas: son, por lo tanto,
termodinàmicamente equivalentes. Este hecho se debe a que exis­
ten procesos que permiten transformar completamente el trabajo
mecánico en energía eléctrica y viceversa.
Como ejemplo de un sistema que puede efectuar trabajo eléc­
trico estudiaremos en este parágrafo la celda electrolítica reversi­
ble. Entendemos por “ celda electrolítica reversible” una celda
tal que una inversión de la dirección de la corriente que fluye
a través de ella invierte también el sentido de las reacciones quí­
micas que se producen en su interior. Una celda reversible siem­
pre se puede llevar a su estado inicial invirtiendo el flujo de la
corriente que circula a través de ella.
Sea V la fuerza electromotriz de la celda. El trabajo eléc­
87
trico que efectúa la celda cuando circula a través de ella una can­
tidad e de electricidad es:
L = ev.
(132)
Por supuesto que la celda realiza esta cantidad de trabajo solo
en el caso de que la cantidad de corriente que circula a través
de ella es muy pequeña, es decir, si el proceso se verifica efec­
tivamente en forma reversible. De lo contrario, una parte de la
energía se transformará en calor dentro de la celda, como resul­
tado del efecto Joule.
Sea Í/(T) la energía de nuestra celda antes de hacer pasar
una corriente eléctrica a través de ella. Suponemos que U{T)
depende solo de la temperatura, ya que consideramos que el volu­
men de la celda es prácticamente invariable (celda isocora) y
despreciamos en consecuencia todos los posibles efectos de la pre­
sión sobre la energía.
Consideremos ahora el estado de nuestra celda después del
pasaje de una cantidad de electricidad e. El flujo de electricidad
a través de la misma da como resultado ciertos cambios químicos
dentro de la celda, y la cantidad de substancia químicamente
transformada es proporcional a e. Es así que la energía de la
celda, U ( T ) , variará en una cantidad proporcional a e. Expre­
sando como U(T,e) la nueva energía de la celda, tenemos:
U(T,e) = U { T ) — eu{T),
(133)
siendo w(T) el decremento de la energía de la celda cuando la
atraviesa una cantidad unitaria de electricidad.
Aplicamos ahora la isocora de van’t Hoff (117) a la trans­
formación isotérmica desde el estado inicial, cuando aún no se
ha producido el pasaje de electricidad a través de la celda (ener­
gía = U{T) ) , hasta el estado final en el cual la ha atravesado la
cantidad de electricidad e (la energía en este caso está dada por
(133)). De (133) se deduce que la variación de energía es:
A U = — eu(T)
El trabajo que se efectúa está dado por (132). Substituyendo en
(117) y dividiendo ambos miembros por e, obtenemos:
<134 )
Esta ecuación, que se conoce como ecuación de Helmholtz,
establece una relación entre la fuerza electromotriz y la energía
u. Hacemos notar que si no se produjera un intercambio de calor
entre la celda y el medio circundante, debería ser v = u. El tér­
mino adicional T d v /d T en (134) representa el efecto del calor
absorbido (o entregado) por la celda al medio circundante cuando
circula por ella una corriente eléctrica.
Podemos también obtener (134) directamente, sin utilizar
la isocora de van’t Hoff. Conectamos la celda a un condensador
variable con una capacidad C. La cantidad de electricidad que
absorbe el condensador es;
e = Cv(T).
Consideremos ahora a C y T como las variables que definen el
estado del sistema compuesto por la celda y el condensador. Si
hacemos variar la capacidad de éste en una cantidad dC, despla­
zando sus placas, el sistema efectúa una cierta cantidad de tra­
bajo a causa de la atracción entre ellas. Esta cantidad de traba­
jo es: 2
dL^VzdCv^T).
La energía de nuestro sistema es la suma de la energía (133)
de la celda,
. U( T) — eu(T) = U { T ) — Cv ( T) u{ T) ,
y la energía del condensador, Y zC v^iT). Por la primera ley de
la termodinámica, vemos que el calor que absorbe el sistema en
una transformación infinitesimal durante la cuaí T y C varían en
dT y dC es:
dQ = dU + dL = d[U{T) - Cv{T)u{T) + ^Cv\T)] + ^dC v\T)
j_rd í7
^ du
^
dv , ^
dv~
+ dC[v^ — uó\.
2
Esta fórm ula se obtiene como sip'ue: la energía de un condensador
aislado e s V2 eVC. Si variam os C, el trabajo efectuado e s igual a m enos la
variación de energía, es decir,
<¡1, donde e se m a n tien e c o n sta n te porque el condensador está aislado.
e = Cv, o b ten em o s la fórm ula utilizada en el texto.
Como
89
El diferencial de entropía es, por lo tanto,
T
fí ■
+ Y [v" - uvl
T
■
’■íí
Dado que dS debe ser un diferencial exacto, tenemos
dU
d dT
dC
^ du
^
T
dv , ^ dv
d f^
df
d v^~uv
dT
T
'
Si efectuamos las derivaciones indicadas y recordamos que
U, u y V son funciones de T únicamente, obtenemos (134).
Problemas
j ■
1. Con ayud a de la regla de la s fases, analizar el equilibrio d e ü n a
solución saturada y el sólido de la substancia disuelta.
2. ¿Cuántos grados de libertad tien e un sistem a co m p u esto por una
cierta cantidad de agua y u n a cierta cantidad de aire? (D esp reciar los
gases raros y el dióxido de carbono que contien e el aire.)
3. La fuerza electrom otriz de un a celda electrolítica reversible, com o
función de la tem peratura, es:
0,924 + 0,0015 t + 0,0000061 í" volts,
siendo t la tem peratura en °C. H allar el calor absorbido por la celda cuand o
un culom bio de electricidad flu y e a trav és de ella isotérm icam ente a una
tem peratura de 18° C.
90
CAPITULO VI
REACCIONES EN SISTEMAS GASEOSOS
21. Equilibrio químico de los gases
Consideremos un sistema gaseoso constituido por una mez­
cla de hidrógeno, oxígeno y vapor de agua. Cada componente
de este sistema puede interactuar químicamente con los demás
de acuerdo con la siguiente reacción química:
2 Ha + Oo ±5 2 H, O.
El símbolo s=y significa que la reacción puede efectuarse de iz­
quierda a derecha (formación de agua) o de derecha a izquierda
(disociación de agua). Es bien sabido que, debido a las leyes de
la química, dadas una temperatura y presión cualesquiera, se al­
canza un estado de equilibrio para el cual la cantidad total de
vapor de agua presente permanece invariable. Es entonces evi­
dente que no se produce disociación ni formación de vapor de
agua. El estado real de cosas que existe en este punto de equili­
brio es tal, que la reacción indicada anteriormente se produce
con igual velocidad en ambas direcciones, de modo que la suma
total de Ho O presente permanece constante. Si después de al­
canzado el equilibrio extraemos del sistema un poco de vapor
de agua, la reacción de izquierda a derecha se producirá con ma­
yor velocidad que una reacción de derecha a izquierda, hasta que
se haya formado una cantidad adicional de Ho O suficiente para'
restablecer un nuevo estado de equilibrio. Si en cambio agrega­
mos vapor de agua, la reacción que adquiere preponderancia du­
rante cierto tiempo será la de derecha a izquierda. El equilibrio
químico en los sistemas gaseosos está regulado por la ley de
acción de masas.
Escribimos la ecuación de una reacción química en la forma
general :
n^Ai + ^2-4.2 + · · · + UrAr^mi By + niiBi + ' · ’ +
(135)
91
u
lí
,j
r* '
,í
•
donde Ai, Aj, . . ., A^ son los símbolos que representan a las mo­
léculas que reaccionan por un lado y Bi, Bg, .. ., Bg los que representan a las moléculas que reaccionan por el otro. Las cantidades ni, n^, . .
y mi, Ttio, .. . son los coeficientes enteros de
la reacción. Designaremos las concentraciones de las diferentes
substancias expresadas en moles por unidad de volumen con los
símbolos [A l], [A 2],
y [Bi], [ B 3 ] , . . . Podemos enunciar
ahora la ley de acción de masas de la siguiente forma:
♦
’I
Cuando en una reacción química se alcanza el equilibrio, la
expresión
1
[A ir
^
[ B i r [ B , r · · · IB.]"'
es función de la temperatura solamente.
La cantidad K{T) puede tomar valores muy distintos en las
diferentes reacciones químicas. En algunos casos será muy pe­
queña, y el equilibrio se desplazará entonces hacia el segundo
miembro; esto significa que una vez alcanzado el equilibrio en
tales casos, las concentraciones de las moléculas en el segundo
miembro son mucho mayores que las de las moléculas en el pri­
mero, Si en cambio K( T) es grande, existe una situación opuesta
a la que hemos descrito anteriormente.
Es instructivo ofrecer una simple demostración cinética de la
ley de acción de masas. El equilibrio químico de la reacción (135)
podría denominarse adecuadamente “ equilibrio cinético” , ya que
las reacciones entre moléculas continúan produciéndose aun des­
pués de alcanzadas las condiciones de equilibrio. En el estado
de equilibrio, sin embargo, el número de reacciones que se produ­
cen por unidad de tiempo de izquierda a derecha en (135) es
igual al de reacciones que se verifican de derecha a izquierda,
de manera que estos dos efectos opuestos se compensan entre sí.
Calcularemos, por lo tanto, el número de reacciones que se pro­
ducen por unidad de tiempo de izquierda a derecha y lo iguala­
remos al número correspondiente de reacciones realizadas en di­
rección opuesta.
Una reacción de izquierda a derecha puede producirse como
resultado de una colisión múltiple que comprende Tij moléculas
A,, no moléculas A 2 .,.,rir moléculas Ar. Como es obvio, la
frecuencia de estas colisiones múltiples es proporcional a la n^ésima potencia de [A ,], a la Wo-ésima potencia de [Ao] . . ., a
la Tir-ésima potencia de [A^], es decir, al producto
92
[A j" ‘ U í r . . . U r r .
Siendo así, la frecuencia de las reacciones de izquierda a dere­
cha debe también ser proporcional a esta expresión. Como la
temperatura es la que determina la velocidad de las moléculas, el
factor deproporcionalidad, K' {T), será una función de latempe­
ratura. Para la frecuencia de las reacciones que se producen de
izquierda a derecha, obtenemos entonces la siguiente expresión:
K ' m [ A , r [A ^r
· · ·
U rr.
Análogamente, para la frecuencia de las reacciones que se
verifican en dirección opuesta tenemos:
K'*{T) [BJ”“ [B if* · · · [B.r*.
En el equilibrio estas dos frecuencias deben ser iguales:
K'{T)
· · ·
[ArT^ = K " m [ B ^ r [ B ^ r ■ ■ ■ [B.T',
o
[Air
· · · [A.r- _ K"{T)
[Bi]"“ [B2]'"» ·. ■ [B.T' K '{T) *
Esta expresión es idéntica a la ley de acción de masas (136) si
ponemos
.
_
K "iT )
.
Este simple planteo cinético no nos da información acerca de
la función K{T) . Veremos ahora que, aplicando la termodinámica
a las reacciones en fase gaseosa no solo podemos demostrar la ley
de acción de masas independientemente de consideraciones ciné­
ticas, sino que también lograremos determinar la dependencia de
K{ T ) de la temperatura.
22. La caja de reacción de van’t Hoff
Podemos tratar termodinàmicamente el equilibrio de las reac­
ciones en fase gaseosa suponiendo la existencia de membranas
ideales, semipermeables, que gozan de las siguientes propiedades:
93
11■
(1) Una membrana semipermeable al gas A es completamente
impermeable a todos los demás gases. (2) Cuando una membrana
semipermeable al gas A separa dos volúmenes que contienen cada
uno una mezcla de A y algún otro gas, el gas A fluye, a través de
la membrana, de la mezcla en la cual su presión parcial es más
alta, hacia la mezcla en la cual su presión parcial es más baja.
El equilibrio se alcanza cuando las presiones parciales del gas A
a ambos lados de la membrana son iguales.
Adviértase que un gas puede fluir espontáneamente a través
de una membrana semipermeable desde una región de presión total
más baja hacia otra de presión total más alta, siempre que la
presión parcial del gas que pasa a través de la membrana sea más
alta en la región de presión total más baja que en la de más alta
presión total. Por ejemplo, si una membrana semipermeable al
hidrógeno separa una caja que contiene hidrógeno a una atmósfera
de presión de otra caja que contiene oxígeno a dos atmósferas, el
hidrógeno fluirá a través de la membrana aun cuando la presión
total en la segunda caja sea dos veces mayor.
Diremos finalmente que en la realidad dichas membranas
ideales semipermeables no existen. La mejor aproximación a dicho
tipo de membrana es ima delgada hoja de paladio caliente, que se
comporta como una membrana semipermeable para el hidrógeno.
Con el objeto de estudiar las condiciones de equilibrio para
la reacción química (135), describiremos previamente tin proceso
mediante el cual la reacción puede efectuarse isotérmicamente y
en forma reversible. Esto puede llevarse a cabo con la ayuda de
la llamada caja de reacción de van’t Hoff.
Esta caja es un amplio recipiente dentro del cual grandes can­
tidades de los gases A^, Ao, . . . y Bi, B2, . .. se hallan en equilibrio
químico a la temperatura T. Sobre un lado de la caja (el izquierdo
en la fig, 17) hay una fila de r ventanas, la fc-ésima de las cuales,
A, :
i%B,
A.:
: B,
1
Pig. 17
contándolas de arriba hacia abajo, es semipermeable al gas Aj,
mientras que sobre el otro lado (el lado derecho en la fig, 17,
donde hemos supuesto que r = s = 2) hay una fila de s ventanag
i
94
semipermeables, en el mismo orden, a los gases Bi, Bo, . . Ba. Se
han agregado a la parte exterior de las ventanas algunos cilindros
con émbolos movibles, como lo muestra la figura.
Describiremos ahora una transformación isotérmica y rever­
sible de nuestro sistema y calcularemos directamente el trabajo L
efectuado por él durante esta transformación. Sin embargo, de
acuerdo con los resultados del parágrafo 17, L debe ser igual a la
energía libre del estado inicial menos la del estado final de la trans­
formación. Comparando estas dos expresiones de L obtendremos
el resultado buscado.
AI comienzo, nuestro sistema se halla en un estado para el
cual los émbolos en los cilindros, B, sobre el lado derecho de la
caja, están en contacto con las ventanas, de manera que el volumen
de dichos cilindros es igual a cero, mientras la posición en que
se encuentran los émbolos de los r cilindros, A, sobre la izquierda
es tal que el fc-ésimo cilindro contiene ti* moles del gas
(ver
fig. 18), cuya concentración es igual a la concentración, [Afc], de
Fig. 18
95
este gas dentro de la caja. Lag presiones parciales del gas sobre
ambos lados de la membrana semipermeable son por consiguiente
iguales, y existe entonces un estado de equilibrio.
La transformación reversible desde el estado inicial hasta el
estado final puede ser efectuada en dos etapas:
1.
A partir del estado inicial (fig. 18), desplazamos muy l
tamente hacia adentro los émbolos en los cilindros que se encuen­
tran sobre el lado izquierdo de la caja, hasta que todos los gases
que dichos cilindros contienen hayan pasado, a través de la mem­
brana semipermeable, al interior de la caja grande. Al final de
este proceso, el sistema se encontrará en el estado intermedio que
se muestra en la figura 18.
Suponemos que el contenido de dicha caja es tan grande que
la variación relativa en las concentraciones, como resultado de la
entrada de estos gases, es despreciable. Las concentraciones de los
gases A permanecen así prácticamente constantes e iguales a [A i],
[A.] . . . ¡Ar].
El trabajo L que efectúa el sistema durante esta etapa es evi­
dentemente negativo, ya que debe realizarse trabajo sobre los pis­
tones, en contra de las presiones de los gases. En el primer cilindro
la presión permanece constante e igual a la presión parcial pi del
gas A-¡ dentro de la caja, mientras que el volumen del cilindro
varía desde el volumen inicial
hasta el volumen final 0. El
trabajo es igual al producto de la presión c mstante pi por la
variación en volumen, es decir, pi (O — V i) = — pi Vi. Como el
contenido del cilindro era inicialmente de ni moles, tenemos, por
la ecuación de estado: P \V i = rixRT. Efectuando la suma del
trabajo sobre todos los cilindros de la izquierda tenemos:
T
Li = — RT ^2
í-l
^
«
jg
í
2.
A partir del estado intermedio, de
mente y hacia afuera los émbolos en los s cilindros que se hallan
sobre el lado izquierdo de la caja (se encuentran inicialmente en
contacto con las ventanas). Como la base del /c-ésimo cilindro,
contando desde el borde superior de la caja, es semipermeable al
gas fífr, durante el proceso, ese cilindro absorberá el gas B^, y su
concentración en el mismo será igual a la del gas dentro de la caja,
es decir, igual a [B/J. Desplazamos los pistones hacia afuera hasta
que los cilindros, siempre siguiendo el orden de arriba hacia abajo,
contengan m¡, m 2 , . . mg moles de los gases Bi, B¿, . . B,, respectivamente.
Llegamos así al estado final de nuestra transformación, como
96
lo muestra la figura 18. En ella vemos que, en el estado final, los
cilindros A tienen sus émbolos en contacto con las paredes, de
manera que su volumen es cero, mientras que la posición de los
émbolos en los cilindros B es tal que el fc-ésimo cilindro, siguiendo
el orden de arriba hacia abajo, contiene m* moles del gas
con
una concentración igual a la concentración, [Bfc], del gas que está
dentro de la caja. Los gases B^, Bo, . . ., B¡, en los cilindros y la
caja, se hallan por lo tanto en equilibrio a través de las bases semi­
permeables de los cilindros. Evidentemente el trabajo efectuado
por el sistema durante esta segunda etapa es positivo.
Podemos calcular este trabajo Ln en la misma forma que he­
mos calculado Lj. Tendremos:
Lqj = R T S yTTlj.
El trabajo total que se realiza durante toda la transforma­
ción es la suma de Li y L,i, es decir.
Este trabajo es igual a la diferencia entre la energía libre de
los estados inicial y final. Con el objeto de calcular esta diferencia,
hacemos notar que el contenido de la caja es el mismo en ambos
estados. En efecto, pasando de un estado.a otro hemos intro­
ducido en la caja rii moles de Ai, rio moles de A>, . . . ,nr moles de
Ar (primera etapa), y luego hemos extraído m i moles de Bi, 7^2
moles de Bo....... m^ moles de B,· Pero la ecuación química (135)
expresa que las substancias introducidas en la caja son equivalen­
tes a las extraídas de la misma. Además, como la temperatura y
el volumen de la caja no varían, el equilibrio químico de los gases
encerrados en ella se readapta de modo tal que los estados inicial
y final de esos gases sin idénticos. La única diferencia entr^
ambos estados del sistema está en el contenido de los cilindros.
Por lo tanto, la diferencia entre la energía libre de los dos estados
es igual a la diferencia entre la energía libre de los gases A ence­
rrados en los cilindros A en el estado inicial y la energía libre de
los gases B encerrados en los cilindros B en el estado final.
La energía libre de los ni moles de Ai en el primer cilindro
(estado inicial) puede calcularse del siguiente modo. El volumen
ocupado por un mol de gas es evidentemente igual a la inversa
de la concentración [A i]. La energía libre de un mol de A i se
obtiene entonces a partir de (119) substituyendo en dicha ecua97
ción l / [ A i ] para el volumen V de un mol. Dado que tenemos ni
moles de A^, la energía libre de este gas es:
71, {Cyi T +
I-
— T(Cvi log T — ñ log [A,] + a ,)} ,
¡
donde Cyi; Wi y aj son el calor molecular y las constantes de
energía y entropía del gas A^. Usando notaciones similares para
An, .. . Ar, encontramos, para la energía libre de los gases A contenidos al comienzo en los cilindros A, la expresión:
1
I
53 rii {C n T + W i — T iP n lo g T — R log U<] + ai)}
i-l
fj ·
Análogamente, la energía libre de los gases B en los cilindros B
al final del proceso se representa por la expresión:
¿ m,· (CryT + w ; - T{Cy,· log r - fí log [B,] + a'^)],
donde C'yj, W'j y a'j son el calor molecular y las constantes de
energía y entropía del gas B¡.
La diferencia entre estas dos expresiones debe ser igual al
trabajo L dado por (137). Tenemos entonces:
R t ( Í L m,· - ¿ n ,) = ¿
\j-l
í-1
/
i-l
ni {G'r. r*+ Wi - T{Cyi log
T
»
- R log U i] + ai) ¡ - ^ m , · {Cy, T
-f W'i - n C y i lo g T - R log [Bi]
+ a;)
(138)
Dividiendo por R T y pasando de logaritmos a números, esta
ecuación se reduce a:
X T
2 Cv<n,- 2 C ' y ¡ m j )
i-l
,·-!
/
<
r
i
2 n.H’i- 2
_ i---- ----------X e
98
(139)
El segundo miembro de esta ecuación es una función de T
solamente. Por consiguiente, la ecuación (139) no solo demuestra
la ley de acción de masas (136), sino que da también explícita­
mente la forma de la función K ( T ) .
Estudiaremos la fórmula (139) más en detalle en el pará­
grafo 24. En el que sigue daremos otra demostración de la misma.
23. Otra demostración de la ecuación de equilibrio de sistemas
gaseosos
En este parágrafo deduciremos la ecuación (139) utilizando
el resultado obtenido en el parágrafo 17, que establece que los
estados de equilibrio de un sistema a una temperatura y volumen
dados son aquéllos para los cuales la energía libre es un mínimo.
Consideramos una mezcla de los gases Au . . . , A , y Bj, .. ., B*
a la temperatura T, encerrados en un recipiente de volumen fijo V
y reaccionando químicamente en concordancia con la ecuación
(135). Cuando una cantidad de los gases contenidos en el reci­
piente interviene en la reacción química, las concentraciones de los
distintos gases presentes varía; como resultado de esto, varía tam­
bién la energía libre de la mezcla. Obtendremos ahora la condición
de equilibrio para la reacción química, haciendo que la energía
libre sea im mínimo. Para eso, debemos obtener la expresión de
la energía libre de una mezcla de gases de concentraciones dadas.
La ley de Dalton (ver par. 2) expresa que la presión de una
mezcla de gases ideales es la suma de las presiones parciales de los
componentes de la mezcla (la presión parcial de uno de los compo­
nentes es la presión que éste ejercería si ocupara él solo el volumen
total que ocupa la mezcla). Esta ley indica que cada componente
no es afectado por la presencia de los otros y conserva así sus pro­
piedades dentro de la mezcla. Generalizaremos ahora la ley de
Dalton suponiendo que en una mezcla de gases ideales la energía
y la entropía son iguales a la suma de las energías y entropías
(energías parciales y entropías parciales) que cada componente
tendría si ocupara él solo el volumen que ocupa la mezcla y a la
temperatura de la misma.
De las definiciones (111) y (121) de la energía libre y el
potencial termodinàmico a presión constante se deduce de inme­
diato que, para una mezcla de gases ideales, estas cantidades son
iguales, respectivamente, a la suma de las energías libres y de los
potenciales termodinámicos parciales a presión constante de los
componentes de la mezcla.
Planteadas estas hipótesis, podemos ahora escribir la expre­
sión de la energía libre para nuestra mezcla de gases. La energía
99
■ T '
It
( ;■
libre de un mol del gas A, està dada, como cn el paràgrafo prece­
dente, por la expresión:
C nT + TFi — jT(Cfi log T — R log [Al] + ai).
!
Como la concentración de Ai en el volumen V es [A i], se
encuentran presentes en total V [A i] moles del gas Ai.
La energía libre parcial correspondiente a este componente
de nuestra mezcla es, por lo tanto:
VlA:]¡Cr:T + TTi - T(Cn ¡og T - R log [All + Oí)}.
La energía libre de todo el sistema se obtiene sumando las energías
libres parciales de los componentes de la mezcla. Obtendremos así
para la energía libre total la expresión:
F
=
FE
[^ i]
+
vE
[B,] {Cy,T + w ; - T(Cy, l o g T - R log [B,] + a,·)} (140)
i-l
í Cy.T + W i - T(Cy.· l o g T - R log [A,-]
+
a ,)}
;-i
¡}··*
Consideremos ahora una reacción infinitesimal del tipo (135),
es decir, una reacción en la cual la cantidad de substancia que se
transforma es infinitesimal. Si la reacción tiene lugar desde la
izquierda hacia la derecha de (135), desaparecen cantidades infi­
nitesimales de los gases Ai, Aj, .. ., A^ al tiempo que se forman
cantidades infinitesimales de los gases B¡, B¿,
Las frac­
ciones de moles de los gases Ai, Ao, . . ., Ar que desaparecen son
proporcionales a los coeficientes ni, n-j, . . ., rir, respectivamente;
mientras que las fracciones de moles de los gases Bi, Bz, . . ., B*
resultantes de la transformación son proporcionales a los números
TTii, 7712, . . ., ms, respectivamente. En consecuencia, las concentra­
ciones [A l], [Ao], . . ., y [B i], [Bo], . . . varían en;
€7 71 ,
1'
siendo e la constante infinitésima de proporcionalidad.
Si F fuera un mínimo de nuestro estado, la variación de F
como resultado de la reacción infinitesimal debe ser nula. Dado
que esta variación puede ser calculada como si se tratara de una
diferencial, tenemos:
100
dF
dF
- aTO
dF
. dF
----------á[I7]^^^ + m ]
dF
.
M
dF
,
+ ^ 1 ''" ·+
■■· + aTO
Dividiendo esta ecuación por eV, y reemplazando las derivadas por
sus valores calculados a partir de (140), obtenemos la siguiente
ecuación:
-
£ n.· {CviT + Wi - nCvi log T - E log[^,.] + a,) + RT]
+ 't m , - { C y , T + W'i - T{Cy,·log T - R \ o g [B,] + a,·) + RT] =0.
>■-1
Es evidente que esta ecuación y la (138) son idénticas. La
ecuación de equilibrio puede obtenerse de inmediato, por el camino
seguido en el parágrafo precedente.
24. Discusión del equilibrio de sistemas gaseosos
El principio de Le Chatelier
Partiendo de (136) y (139) podemos obtener la forma explí­
cita de la función K ( T ) , que aparece en el segundo miembro de
(136). K{T) es a veces llamada la constante de la ley de acción
de masas; por supuesto que solo es una constante cuando la tempe­
ratura es constante. Comparando (136) y (139) se tiene:
i!
2
2 (Λ+Cvi—a»)n,
K(T) = e
Σ
X
T
Σ C'v;"·,·
Σ ". W'i- Σ
B^',· )
/
(141)
Con el objeto de estudiar cómo depende K (T ) de la tempera­
tura, definiremos primero el calor de reacción H de la reacción
química (135). Consideremos una mezcla de los gases A y B a
temperatura fija y volumen constante. Supongamos que estos
gases reaccionan de acuerdo con la ecuación (135), de manera
que ni, n¡ . . ., n^ moles de los gases Ai, Ao, . . ., Ar, interactúan y
dan lugar a la formación de mi, m^, . . ., m¡ moles de los gases Bi,
101
Bn, . . . ( Bs, respectivamente. El calor H desarrollado por el siste­
ma durante este proceso isotérmico es el calor de reacción a
volumen constante. La reacción será exotérmica o endotérmica, y
ello depende de si el sistema entrega o absorbe calor cuando aquélla
se dirige de izquierda a derecha en la ecuación (135).
Como la reacción se efectúa a volumen constante, el siste­
ma no realiza ningún trabajo. Por lo tanto, el calor absorbido
( = — H) será, de acuerdo con la primera ley (15), igual a la
variación AU de la,energía del sistema:
H = -A U .
Si se tiene en cuenta que la energía de un mol de Ai, por
ejemplo, es igual a Cvi T
Wi, y que el número de moles de los
gases Al, An, . . . , A r y Bi, B^, .. ., B¡ se incrementan en — Ui,
— ^2 · ■., ■
— Ur y mi, m~2 , . . m„ respectivamente, como resultado
de la reacción, se verifica que la variación de energía asociada
a (135) está dada por la expresión:
AC7 = ¿ ruiiCyiT + w'i) - É n.(Cr. T + W,).
i-i
t-i
El calor de reacción será entonces:
H =
UiiCviT + íí^·) - ¿ mACviT + w'i).
(142)
Tomando la derivada logarítmica de (141), obtenemos:
T
r
g
d log K (T )
Cviiii
df
= —
Cyj'nij
j_
WiTii
+-
53 WjTn,·
^2
De esta ecuación y (142) resulta:
d log K iT )
dT
H
RT^'
(143)
Esta ecuación, que fue deducida por Helmholtz
expresa
claramente que K (T ) es una función creciente o decreciente de
T, según que el calor de reacción sea positivo o negativo; K (T )
^ Esta ecuación puede deducirse directam en te aplicando la isocora de
van ’t Hoff (317) a un proceso sim ilar al descrito en el parágrafo 22.
102
aumenta con la temperatura cuando se trata de reacciones exotér­
micas y disminuye con dicho aumento cuando las reacciones son
endotérmicas.
Podemos observar fácilmente, en la ecuación (136), que un
aumento de K {T ) origina un cambio de las condiciones de equili­
brio en la dirección de las concentraciones crecientes de los
gases A y decrecientes de los gases B, es decir, un desplazamiento
del equilibrio desde la derecha hacia la izquierda de (135). Por
otra parte, si K {T ) disminuye, el equilibrio se desplaza de la
izquierda hacia la derecha en dicha ecuación.
El efecto de los cambios en las condiciones externas de una
reacción química sobre el estado de equilibrio de la misma puede
resumirse muy bien en el principio de Le Chatelier. Este principio,
que nos permite determinar sin cálculos la dirección hacia la cual
una variación en las condiciones externas tiende a desplazar el
equilibrio de un sistema termodinàmico, establece lo siguiente:
S i se alteran las condiciones externas de un sistema termodinámico, el equilibrio del sistema tenderá a desplazarse en una
dirección tal que le permita oponerse a la variación en las condi­
ciones externas.
Algunos ejemplos servirán para aclarar el significado de este
enunciado. Hemos visto ya que si la reacción (135) es exotér­
mica, un aumento en la temperatura produce un desplazamiento
del equilibrio químico hacia el primer miembro de la ecuación
(135). Dado que la reacción de izquierda a derecha es exotérmica,
en el desplazamiento del equilibrio hacia la izquierda el sistema
absorbe calor y así se opone al aumento de la temperatura.
Como segundo ejemplo de la aplicación del principio de Le
Chatelier estudiaremos el efecto que produce un cambio en la
presión (a temperatura constante) sobre el equilibrio de la reac­
ción (135). Podemos advertir que si la reacción (135) está diri­
gida de izquierda a derecha, el número de moles de nuestro sistema
en fase gaseosa varía; si
Wi +
+ · · · 4- rir < mi + mz + —
m,,
(144)
el número de moles aumenta. En caso de que el primer miembro
de esta desigualdad sea mayor que el segundo, el número de moles
disminuye. Si suponemos que la desigualdad (144) se cumple,
el desplazamiento del equilibrio hacia la derecha producirá un
aumento en la presión y viceversa. De acuerdo con el principio
de Le Chatelier debemos suponer entonces que un aumento en la
presión de nuestra mezcla de gases producirá un desplazamiento
103
I
l
»*.
>;
i
I
'i
I
i
,j
!|
del equilibrio bacia la izquierda, es decir, en la dirección que per­
mite . al sistema oponerse al aumento de la presión. (En general un aumento de la presión desplazará el equilibrio en la
dirección en que el número de moles del sistema disminuye. Una
disminución en la presión lo desplazará en la dirección en que el
número de moles aumenta.) Veremos ahora que este resultado
puede obtenerse directamente de la ley de acción de masas (136).
Si aumentamos la presión en nuestro sistema manteniendo
la temperatura constante, las concentraciones de los componentes
de la mezcla de gases aumenta. Si esta modificación no afectara
el equilibrio químico, las concentraciones de todos los componentes aumentarían en un mismo, factor, y suponiendo que se cumple
(144) deberíamos esperar una disminución del primer miembro
de (136). Esto no es posible, ya que la expresión en el segundo
miembro de (136) permanece constante. Por lo tanto, para man­
tener también constante el primer miembro de (136) el equilibrio
debe desplazarse hacia la izquierda.
Para concluir este parágrafo diremos que en general las
bajas presiones favorecen los procesos de discoiación, mientras
que las altas facilitan los procesos de combinación.
Problemas
1. Para una reacción qu ím ica del tipo :
't\
2 A — Ai
la con stan te de equilibrio K { T ) de la le y de acción de m asas a la tem peratura
de 18° C es 0,00017. La presión total de la m ezcla de gases e s de 1 atm ós­
fera. H allar el porcen taje de m olécu las disociadas.
2. Sabiendo que el calor de reacción para la reacción considerada en el
problem a 1 es 50.000 c a l/m o l, encontrar el grado de disociación a 19° C y
1 atm ósfera.
L
104
CAPITULO v n
TERMODINÁMICA DE LAS SOLUCIONES DILUIDAS
25. Soluciones diluidas
Llámase diluida a una solución cuando la cantidad de soluto
es pequeña comparada con la de solvente. En este parágrafo desa­
rrollaremos los principios fundamentales de la termodinámica de
las soluciones diluidas.
Consideremos una solución compuesta por N qmoles de solvente
y Ni, No, . . -jNg moles de las varias substancias disueltas Ai,
An, . . ., Ag, respectivamente. Si la solución está muy diluida, ten­
dremos ;
N i « iVo; N z « N o ; · · ; N , «
N o.
(1 4 5 )
Nuestro primer problema será encontrar las expresiones para
la energía, el volumen, la entropía, etc. de la solución diluida. Una
aplicación directa de las ecuaciones termodinámicas evidenciará
entonces todas las demás propiedades de la solución diluida.
En primer lugar consideremos la energía U de nuestra solu­
ción. Sea u la energía de una fracción de la solución, que con­
tiene un mol de solvente. Esta fracción contendrá N i / N q moles
del soluto A u N-JN^ moles del soluto An, . . Nf,/No moles del so­
luto Ag. Su energía será función de T, p, y de las cantidades
------es decir:
Como la cantidad de moles de solvente que contiene toda la
solución es No, su energía U es No veces mayor que (146); ten­
dremos entonces
105
Teniendo en cuenta que por tratarse de una solución diluida
las relaciones N j/ N q, N ^/N q, . .., Ng/No son muy pequeñas, supon­
dremos ahora que es posible desarrollar la función (146) en poten­
cias de esas relaciones, despreciando los términos elevados a una
potencia mayor que la primera. Obtenemos así:
m
= M T , p) +
Si
M T , p) + ^ M T , p ) + - - - +
p).
Si substituimos esta expresión en (147), tendremos que:
U = NoUoiT, p) + NiUiiT, p) + " · + NgUgiT, p)
= ílN iU ¿ T ,p ).
t-O
(148)
Debemos hacer notar que aunque los diversos términos en la
expresión (148) son formalmente muy similares, el primero es
mucho mayor que los demás, a causa de las desigualdades (145).
Mediante un proceso de razonamiento similar, podemos de­
mostrar que, dentro del mismo orden de aproximación, la expre­
sión para el volumen es:
V = N M , p) + N M T , p) + ·. . + N M T , p)
= t,N M T ,p ).
(149)
i-0
Debemos obtener ahora la expresión para la entropía de
nuestra solución. Con ese objeto consideramos una transforma­
ción infinitesimal reversible durante la cual T y p varíem. en can­
tidades infinitesimales dT y dp, mientras que las cantidades No,
Ni, .. .,Ng no varían. La variación de entropía resultante de esta
transformación es:
ds = ^
= l ( d u + pdr)
= ¿ J V ,ííi+ J * .
1 -0
f
(150)
1
Dado que dS es una diferencial exacta para todos los valores
de las N, el coeficiente de cada N en (150) debe ser una diferencial
exacta. Integrando estas diferenciales exactas obtenemos un con­
junto de funciones Sq{T, p), S i{T ,p ), . .., Sg (T, p) tales que:
106
dsiiT, p) =
dui + pdvj
Integrando ahora (150), obtenemos la expresión para la en­
tropía :
5 = í : NiSiiT, p) + CCiVo,
»-0
· ·. , N,).
(152)
La constante de integración C, que solo es constante con respecto
a T y p, depende de las N; esto está indicado explícitamente en
(152). Podemos determinar su valor del siguiente modo:
Como no hemos puesto restricciones sobre la forma en que
varían T y p, la expresión (152) para S sigue siendo válida aun
cuando p se haga tan pequeña y T tan grande que toda la solución,
incluidos los solutos, se vaporiza. Nuestro sistema será entonces
un sistema completamente gaseoso, y para tal sistema sabemos ya
que la entropía es igual a la suma de las entropías parciales de los
gases componentes (ver par. 23). Pero la entropía de un mol de
gas a la presión parcial Pi y cuyo calor molecular es Cp-, está dada
por (ver ecuación (8 7 )):
Cpi log T — B log Pi + o,· + 22 log R
(153)
Por lo tanto, para nuestra mezcla de gases tendremos (dado
que la presión parcial p¡ de la substancia A¡ es igual a pNj/(No +
+ . . . + iVp), siendo p la presión total):
= É N i (Cpi l o g T - R log p
^
= ¿ NiiCpi lo g T — R log p + Oí + R log •K)
Í-O
-
r
Í
Ni
Ni log
i-o
iVo - + ' · ■ · +
Ng
Si comparamos esta expresión con (152), que es también
aplicable a la mezcla gaseosa, tenemos:
»< = Cpi log T
R log p + Ot + fi log R,
y
C i N o , N i , ‘ ·· , N , ) = - R Í N i l o g ^ ·
í-o
No + · ■ · + Ng
.
(154)
107
y
Pero la constante C (N q, N i , . . ,,Ng) es independiente de T
y p. Su valor (154) es válido no solo para la mezcla gaseosa, sino
también para la solución original. En consecuencia (152) se convierte en:
'!
S ° ¿ NM T,
i-0
log ■
i-0
■
No +
Ni
+
Ng
(155)
Es convenierite simplificar el último término de (155) tenien­
do en cuenta las desigualdades (145). Despreciando los términos
de orden mayor que esprimerò en las pequeñas cantidades Ni,
N^, . . ., Nff, vemos que :
g ,,-4 ^----- ^ = N o l o g
No + N i + - - - + N g
ATo l o
^
_^Ng
No
No~^
\
Ni
Ni
No
No
= -N i-N ^
Ng\
■ ■■
No)
-------------------- Ng ,
y que:
+
(toríSl).
Por lo tanto
.
:
S = N oS oiT , p ) +
t , N ilsiiT , p) +
i-l
fí} -
f í ¿ JV, l o g
í- 1
No
En lugar de las funciones s, introducimos ahora las nuevas
{unciones:
ao{T,
j;
p)
= So{T,
p)
=
S i{T , p ) + R
p)
=
$2{T, p ) +
<rÁT, v )
= Sg{T,
p)
p)
+
R
(156)
R.
Tenemos entonces:
5 = ¿
d.
i=o
108
Ni<n{T, p) -
r
Í
i-l
Ni log
No
(157)
(Nótese la diferencia entre los límites de las dos sumatorias.)
Aunque las cantidades m,, v», y ctí son, hablando estricta­
mente, funciones de T y p, en general variaciones de la presión
producen cambios muy pequeños en dichas cantidades y, por lo
tanto, en la práctica Ui, Vi y <tí pueden considerarse como fun­
ciones de T únicamente.^
En la teoría de las soluciones diluidas utilizaremos siempre
estas aproximaciones. Por lo tanto, escribiremos (148), (149) y
(157) como sigue:
U = i NiUiiT)
í—O
^
7 = ¿ NM T)
i-O
s = t , Ni<T¿T) i-O
r
Í N
í log
(158)
» -1
Con estas expresiones para U, V y S, podemos escribir de
inmediato las fórmulas para la energía libre F y el potencial ter­
modinàmico ^ (ver ecuaciones (111) y (121)). Tenemos:
F = ¿
N iM T ) -
TaiiT)] + R T Í : N i
í-o
i- l
= ¿ N iM T ) - ^ R T i , N i log ^ ,
i-O
í-l
log ^
iV o
(1590
iVo
donde
fi{T) = Ui{T) - TaiiT);
(160)
1
Considerar que Vi e s in d ep en d ien te de p equivale a despreciar la pe­
queña com presibilidad de los líquidos. A nálogam ente, u* es casi ind ep en­
d iente de p; en efecto si com prim im os isotérm icam en te u n líquido, sabem os
por experiencias que el calor desarrollado es despreciable. El tr a b a jo -e s
tam bién despreciable debido a la p equ eñ a variación de volum en. Se deduce
entonces, por la prim era ley , q u e la variación de energía e s m uy pequeña.
Para dem ostrar que tam bién o", es prácticam en te ind ep en dien te de p, obser­
vam os, c o n 'la ayud a de (1 5 6 ) y (1 5 1 ), que:
díTidsi _ l/ dui
dp
dp
íT \9 p
8t>í\
^/
Dado q u e Ui y Vi son p rácticam en te independientes de p, las derivad as par­
ciales del segundo m iem bro se pueden despreciar. En consecuencia (6<^i/6p)
es m u y pequeña y
puede considerarse com o dependiente de T únicam ente.
109
4> = ¿ NAuiiT) - Ta¿T) + yvAT)] + R t Ì
ì-0
"x;
Ȓ
= ¿ Ni[U iT) + vvi{T)] +
♦*0
( 161)
¿ Ni log
i-l
Ni log ^
N,
iVo
26. Presión osmótica
t,·
hi*:
En lo que respecta a las soluciones, definiremos como mem­
brana semipermeable a una membrana permeable al solvente e
impermeable a los solutos. En la naturaleza se encuentran con
frecuencia membranas semipermeables para soluciones acuosas.
Por ejemplo, las. membranas de las células vivas son a menudo
semipermeables. Una membrana artificial semipermeable muy
conveniente es una delgada capa de ferrocianuro de cobre adhe­
rida al interior de una pared de material poroso.
fó‘.
----- C-
ilición
i
Fig. 19
5
ì
I
Cuando una membrana semipermeable separa una solución
del solvente puro, existe en el estado de equilibrio una diferencia
de presión entre la solución y el solvente puro. Esto puede ser
demostrado mediante un experimento muy sencillo.
Colocamos dentro de un recipiente de paredes semipermea­
bles una solución de azúcar en agua. A través de la pared superior
del recipiente insertamos un tubo vertical, como se ve en la figura
19, en la cual las paredes semipermeables del recipiente están
indicados por líneas de puntos. La altura del menisco en este
tubo indica la presión de la solución dentro del recipiente. Sumer­
gimos ahora el recipiente en un baño de agua pura, y observamos
que el menisco dentro del tubo se eleva por encima del nivel del
agua. Esto indica que parte del agua del baño ha pasado a la
solución. Se llega al equilibrio cuando el menisco en el tubo al110
canza una cierta altura h sobre el nivel del baño de agua, lo que
pone en evidencia que la presión en la solución es más elevada
que la presión en el agua pura. Esta diferencia de presión es la
llamada presión osmótica de la solución. Si despreciamos la pe­
queña diferencia entre la densidad del agua y la densidad de la
solución, la presión osmótica es igual a la presión que ejerce
la columna líquida h, y está dada por el producto:
altura, h
X
densidad
X
aceleración de la gravedad.
La utilización dél resultado general de que el trabajo efec­
tuado por un sistema durante una transformación isotérmica
reversible es igual a menos la variación de la energía libre nos
permite obtener termodinamicamente la expresión para la presión
osmótica. Consideremos el sistema representado en la figura 20.
Un recipiente cilindrico está dividido en dos partes por una mem­
brana semipermeable EF paralela a las bases AB y CD del reci­
piente. La parte de la izquierda de éste está llena de una solución
compuesta de N q moles de solvente y Ni, Nn, ■ . N¡, moles de va­
rias substancias disueltas.
Solvente
Solución
puro
F
Fig. 20
La parte de la derecha está completamente llena con N'o moles de
solvente puro.
Dado que la membrana que separa las dos partes del recipiente
es permeable al solvente puro, habrá un flujo de éste a través de la
membrana en ambas direcciones. Cuando ambos flujos se igualen
el sistema estará en equilibrio y habrá entonces una diferencia
de presión entre las dos partes en que está dividido el recipiente.
Esta diferencia de presión P es igual a la presión osmótica.
Supongamos ahora que la membrana semipermeable es movi­
ble y consideremos una transformación infinitesimal de nuestro
sistema, durante la cual la membrana se desplaza una distancia
infinitesimal hacia la derecha, de modo que el volumen sobre la
izquierda aumenta en la cantidad dV, mientras que sobre la dere111
i i r
cha disminuye en igual cantidad. Como la presión ejercida por la
solución sobre la cara izquierda de la membrana supera en una
cantidad P a la ejercida por el solvente puro sobre la cara derecha,
el trabajo que efectúa el sistema es PdV.
Durante el desplazamiento de la membrana una cierta canti­
dad (dNo moles) del solvente fluye desde la derecha del recipiente
hacia la solución en la izquierda, diluyendo así la solución. Los
volúmenes V y V' de la solución y el solvente puro, respectiva­
mente, previos a la transformación, de acuerdo con la segunda de
las ecuaciones (158), son:
V — NoVo + N\Vl + · · · + NgVg
V' = N'oVü.
( 162)
Si
aumenta en la cantidad dN^, tendremos por la primera
ecuación 2 .
dV = vodNo;
y el trabajo que efectúa el sistema es, por lo tanto:
(163)
PvodNo.
La energía libre de la solución está dada por (159), y es
igual a :
iVo/o + i V i /i +
·· · +
Ngfg
+
Rt ( ni \ o g ^ ^ + . . . + N g
lo g
La energía libre del solvente puro se obtiene a partir de esta fór­
mula reemplazando N q por N' qy poniendo N i = N ‘<= . . . = iV^ = 0.
Esto nos da:
N'ofo.
La energía libre total de nuestro sistema es igual a la suma
de estas dos:
F = (No + N'o)fo + N i f i +
f
I
i
%
t
+ N Jg + R T Z N ilo g ^ \
i-l
-/Vo
Puesto que
y N'^ varían en dN^ y — dNo, respectivamente, como
resultado de la transformación, la variación de F está dada por:
Dado que N'« dism in uye en la cantidad d N n , ten em os d V ’ — — Vo dN
de m odo que el volum en total perm anece invariable.
112
”
^
{
¿ N Ì fd N , - U N ,
JVo i-l
= —
I\0
J
d N o Z N i.
1=1
Esta cantidad cambiada de signo debe ser igual al trabajo (163),
debido a que la transformación es reversible. Así es que:
PvodNo
=
^d N o Z N i,
I\o
i-l
O
PvoNo = R t Í N
i-=l
í
.
(164)
Vg, que es el volumen que ocupan
moles de solvente puro,
difiere muy pòco del volumen V de la solución diluida (ver (145)
y la primera de las ecuaciones (162) ) ; Despreciando esta pequeña
diferencia ^ y reemplazando
por V en (164) se obtiene:
PV = RT i
i-l
Ni^
tj
P = ^ ( N , + N 2 + ---+ N ,).
(165)
(1G6)
Esta expresión de la presión osmótica de una solución se ase­
meja mucho a la ecuación de estado de un gas. La ecuación (166)
puede enunciarse así:
La presión osmótica de una solución diluida es igual a la
presión que ejerce un gas ideal que se encuentra a igual tempera­
tura y ocupa el mismo volumen que la solución y contiene un
número de moles igual al número de moles de los solutos disueltos
en la solución.
3
E s e v id en te que esta aproxim ación consiste en no tom ar en cuenta
los térm in os que con tien en los cuadrados de las concentraciones de los solutos,
y e s por lo tan to com patible con todas las aproxim aciones y a efectuad as en la
teoría de las soluciones diluidas.
113
Este simple resultado termodinàmico puede ser fácilmente in­
terpretado desde el punto de vista de la teoría cinética. Consi­
deremos un recipiente dividido en dos partes por una membrana
semipermeable y que contiene solvente puro en cada una de ellas.
Puesto que el solvente puro puede pasar libremente a través de la
membrana semipermeable, la presión sobre ambos lados de la mem­
brana será la misma. Disolvamos ahora una substancia en una sola
de las partes en que se halla dividido el recipiente. La presión
sobre la cara de la membrana en contacto con la solución aumen­
tará debido a los impactos de las moléculas de la substancia disuel­
ta, que no pueden pasar a través de la membrana y se mueven con
una velocidad que depende de T. Cuanto mayor sea el número de
moléculas disueltas y la temperatura, mayor será el número de
impactos por unidad de tiempo que reciba la cara de la membrana
que enfrenta a la solución y, por lo tanto, mayor la presión
osmótica.
Podemos demostrar, partiendo de la teoría cinética, que las
velocidades de las moléculas de las substancias disueltas no son
afectadas por las moléculas presentes en la solución, sino que son
iguales a las velocidades que tendrían si se encontraran en estado
gaseoso. Es por eso que, tanto el número como la intensidad de los
impactos de las moléculas de las substancias disueltas contra la
membrana son iguales ál número e intensidad de los impactos
que se esperan para un gas. Las presiones que se ejercen en ambos
casos son por lo tanto iguales.
Para calcular la presión osmótica con la ayuda de (166) es
necesario conocer el número total de moles de las substancias disüeltas en la solución. Si no se produce en los solutos ningún
cambio químico como resultado de su permanencia en la solución,
podemos calcularla de inmediato conociendo los pesos moleculares
de los solutos y el porcentaje en peso de estas substancias pre­
sentes en la solución. Por ejemplo, una solución nonnal, es decir,
una solución que contiene 1 mol de soluto por litro de agua, tiene,
a 15° C, una presión osmótica:
'·!
_
R X 288,1
„ ^ ^ , dinas
_
Pnormai = —-------------- 2,4 X 10^--- 23,7 atm.
1.000
cm^
En muchos casos, sin embargo, cuando una substancia se di­
suelve se produce una transformación química, de manera que
el número de moles de la sustancia en la solución no es necesaria­
mente igual al número de moles de la substancia antes de ser di­
suelta. El ejemplo más importante en este caso es el de un electro­
lito disuelto en agua. Cuando se disuelve, por ejemplo, ClNa en
114
agua, casi todas las moléculas se disocian en iones de Na^ y Cl“. El
número de moléculas que se encuentra en la solución es entonces
el doble del número que podría esperarse si no hubiera disociación.
AAgimos electrolitos se disocian, por supuesto, en más de dos iones.
Para los electrolitos fuertes la disociación es prácticamente com­
pleta aun cuando la solución no sea muy diluida. En el caso de
electrolitos débiles, por otra parte, se establece el equilibrio quí­
mico entre la disociación del electrolito en iones y la recombina­
ción de esos iones. La disociación en este caso es, por lo tanto,
incompleta.
27. Equilibrio químico de las soluciones
Hemos visto ya que la ley de acción de masas (136) se aplica
a reacciones químicas que tienen lugar en sistemas en fase gaseosa.
Deduciremos ahora una ley correspondiente para las reacciones
químicas que se producen en soluciones.
Supongamos que Aq representa una molécula del solvente y
Al ,
Ar y Bi, . .
Bs representan las moléculas de los solutos.
Supongamos también que entre dichas substancias puede tener lu­
gar una reacción química definida por la ecuación:
UoA q + UiAi + · · · + TlrAr ^ VliBi + ■ · ' + ITl, B, (167)
Si 7io=^0, el solvente también participa de la reacción, mientras
que si ?io = O son solo los solutos los que reaccionan entre sí.
Como lo hemos hecho en el parágrafo 23, impondremos la
condición de que, cuando se alcance el equilibrio, la energía libre
deberá ser un mínimo.^
La energía libre de una solución será, conforme a (159) :
F = foNo + £ f i N i + £ f ' N '
;=1
+ R T { J : Ni log
ti-l
+ É N- log
A'o
;-l
No)
(168)
en la que fi y f'j son las funciones de T para las substancias disuel­
tas Ai y Bj, que corresponden a las funciones fi, . ■ fg que apa­
recen en la ecuación (159), y N q, N í , y Nj son los números de moles
del solvente y las substancias disueltas Ai y Bj, respectivamente.
^ Dado que las variacion es de volu m en de una solución son siempre
m uy pequeñas, e s in d istin to considerar la condición de equilibrio a presión
con stan te o a volu m en constante.
115
Al igual que en el parágrafo 23, consideramos ahora una reac­
ción isotérmica infinitesimal del tipo (167) como resultado de la
cual, No, Nu .. .,N r y N \ , . . . N's varían en:
11
ni!
>' ' ' ,
—e/lo, —eni, · · · , —
Iti\
,
respectivamente, donde e es una constante infinitesimal de pro­
porcionalidad.
Siendo F un mínimo en el estado de equilibrio, su variación
para el sistema en equilibrio debe ser nula. Tenemos entonces:
V*
dF
dF
Dividiendo por e y calculando las derivadas con la ayuda de la
ecuación (168) (las f son funciones de T únicamente y por lo
tanto no varían durante una transformación isotérmica), encon­
tramos que, despreciando todos los términos proporcionales a las
pequeñas cantidades Ni/No N'j/No:
O = -no/o - É r i i U + R T + R T log
log
\NoJ \NoJ ' ' ’ \ N o /
( N [ Y ( N ',Y
(n :y
\N oJ \ n J
' ' ' \N o J
Z
_ ;·-!
+ fíT ) - É n.(/,· + R T) - n^fo
_____ ______ f-i__________________
RT
El segundo miembro de esta ecuación es solo función de T.
Si lo igualamos a log K ( T ) , siendo K una función conveniente
de la temperatura, obtenemos finalmente :
(169)
116
Ésta ecuación es la e:'presión de la ley de acción de masas para el
equilibrio químico de las soluciones.
El tratamiento de (169) para el caso en que el solvente no in­
terviene en la reacción (es decir, cuando
= O en [167] ) es el mis­
mo que para la ley de acción de masas en los gases (ver par. 24).
En particular, resulta de la ecuación (169) que si diluimos la
solución, el equilibrio se desplaza en la dirección en que aumenta
la disociación. Por supuesto que en este caso no tenemos un medio
simple para determinar la forma de K ( T ) , como lo hicimos en el
de los gases. Sabemos únicamente que K{T) es función de la
temperatura.
Como un ejemplo particularmente importante para el caso en
que el solvente intervenga en la reacción química, consideremos la
reacción :
H^O =
+ OH-,
(170)
o sea la disociación del agua en los iones hidrógeno y oxhidrilo
(hidrólisis del agua). Sean [H^] y [0H~] las concentraciones de
los iones hidrógeno y oxhidrilo (número de moles por cm·'*)· To­
mando un centímetro cúbico de agua tenemos: iVo = — . En con18
secuencia, las relaciones entre el número de moles de [H*·] y [OH"]
y el de moles de agua son, respectivamente, 18[H·^] y 18[0H '].
Aplicando la ecuación ,(169) a la reacción (170), vemos que
‘
3 = K (T),
18=[H+]10H-J
IH+lIOH'i =
= X '(T ),
(171)
donde K'{T) es una nueva función de la temperatura solamente'.
Podemos comprobar, mediante esta ecuación, que el producto
de las concentraciones de los iones hidrógeno y oxhidrilo en agua
es una constante cuando la temperatura es constante.® A tempe® De acuerdo con la ley de acción de m asas aplicada a la reacción (171),
podría esperarse que la relación [H *] [ 0 H “] / [ H - 0 ] fuese una función de T
solam ente. Sin embargo, dado que el denom inador es prácticam ente cons­
tante, el num erador debo ser tam bién una función de T solam ente, de acuerdo
con la ecu ación (1 7 1 ). V em os en ton ces que (1 7 1 ) es esen cialm en te equiva­
len te a la ley de acción de m asas en su forma usual.
117
ratura ambiente, este producto es aproximadamente igual a 10
cuando las concentraciones se expresan en moles por litro, o sea:
[H+][OH~] = 10-^
f*··
d'72)
En agua pura, las concentraciones de
y OH" son iguales,
de modo que en este caso se tiene, por (172) :
[H·^] = [O H I = 10-^
Si agregamos al agua un poco de ácido, se produce un aumento
de [H*], y, como el producto (172) debe mantenerse constante,
hay una correspondiente disminución de [O H '].
Ocurre lo contrario si agregamos una base. Frecuentemente
se indica la acidez de una solución acuosa por medio del símbolo;
pH = - L o g [H+],
(173)
(El símbolo Log representa al logaritmo en base 10; [H*^] se ex­
presa como antes en moles por litro.) Así, pH = 7 indica una
reacción neutra; pH < 7 significa acidez y pH > 7 equivale a una
reacción básica.
La exposición que antecede, referente al equilibrio químico en
las soluciones, es incompleta, ya que no se han tenido en cuenta las
fuerzas electrostáticas entre iones. Debye y Hückel han demostrado
que tales fuerzas son a menudo de gran importancia y pueden
afectar considerablemente la reacción química.
El tratamiento de este tema está, sin embargo, fuera de los
alcances de este libro.
28. La distribución de un soluto entre dos fases
Sean A y B dos líquidos no miscibles (como, por ejemplo,
agua y éter etílico) en contacto. Sea C una tercera substancia,
soluble tanto en A como en B. Si disolvemos una cierta cantidad
de C en el líquido A, la substancia C se difunde a través de la super­
ficie de separación de ^4 y B y, después de un corto intervalo, C
estará en solución en ambos líquidos. La concentración de C en el
líquido B continuará aumentando y la de C en ^4 disminuirá hasta
que se alcance el equilibrio entre ambas soluciones.
Sean N a y N¡, los números de moles de los dos solventes A y B,
y sean N\ y N \ los números de moles del soluto C disuelto en A y
B, respectivamente. El potencial termodinàmico, <5, de nuestro sis^
tema será la suma de los potenciales de las dos soluciones.
I
118
En primer lugar, tenemos una solución de Ni moles de C
disueltos en N a moles del líquido A. El potencial termodinàmico a
presión constante de esta solución es, de acuerdo con (161) :
=
N a Í/ aÍT)
+
W a ÍT)]
+
Ni[MT)
+
pvi{T)\
+ B ™ ,lo g ^ ,
(H 4 )
donde /a,
Va y Vi corresponden a /o, fu Vq y Vi de la fórmula
general (161).
En segundo lugar, tenemos una solución que contiene N b moles
del solvente B y N \ moles del soluto C. Su potencial termodinàmico
está dado por :
» . - N , í f , c n + fv,(T)] + n ' , { A t ) + p v ' m i
+ fin v :io g ^ ,
(175)
donde las cantidades Í b, f \ , Vb y v'i corresponden a /o, fu Vq y Vi
de (161).
_
El potencial termodinàmico í> del sistema completo es:
.
(176)
Para una temperatura y presión dadas la condición de equilibrio
es que $ sea un mínimo.
Consideremos una transformación infinitesimal de nuestro sis­
tema como resultado de la cual una cantidad dNi de C pasa del
líquido B al líquido A. Ni y N \ variarán en las cantidades dNi
y — dNu respectivamente, y la variación de $ estará dada por:
Para que ^ sea un mínimo, esta expresión debe anularse.
Dividiendo por dN obtenemos la ecuación:
dNi
a<í>
dNi
(177)
Utilizando las (176), (175) y (174), tenemos la condición de
equilibrio:
119
,
?¡I’
r
j
M T ) + pv,(T) + R T log
ii
+ RT
7\r'
= A ( T ) + pv¡(T) + R T log ^ ^ + RT,
]
ì
ATi
TT
/t'(r)-/¡(T)+p[v,'(T)-T,(r)¡
^ ,
Sr
= K{T, v),
(178)
Nb
donde la función K {T, p) depende solo de la temperatura y la pre­
sión y no de las concentraciones.
La ecuación (178) expresa la siguiente ley:
Cuando dos soluciones diluidas del mismo soluto en dos sol­
ventes inmiscibles y diferentes están en contacto y en equilibrio,
la relación de las concentraciones de las dos soluciones a una temperatura y presión dadas es constante.
I
.*
^
•j
,!
;
Análogo al que ac,abamos de tratar es el problema siguiente:
Una solución de un gas disuelto en un líquido está en contacto
con el gas mismo. Encontrar la relación entre la presión del gas
y la concentración de la solución para la cual el sistema se halla
en equilibrio a una temperatura dada.
Sean No y
el número de moles del solvente líquido y del'
soluto gaseoso en la solución, respectivamente, y sea N \ el número
de moles de gas en la fase gaseosa. Como las variaciones de volu­
men de la solución son prácticamente despreciables, comparadas
con las variaciones de volumen de la fase gaseosa, podemos no
tomar en cuenta el término pV en la expresión para el potencial
termodinàmico de la solución e identificar este potencial con la
energía libre de la solución. De acuerdo con (159), esto es:
i
N ,f,{T) + N ih iT ) + R T N i log ^ .
?
1
(179)
El potencial termodinàmico de la fase gaseosa se obtiene ds la
ecuación (125) multiplicándola por el número de moles 2V'i del gas :
N [[C j,T-\-W ~ T {C p lo g T - R l o g p + a + R l o g R ) ] .
(180)
./
mico
120
Sumando (179) y (180) obtenemos el potencial termodinà­
del sistema total. Al igual que en el problema precedente
obtenemos la ecuación. (177) como condición de equilibrio. Substi­
tuyendo las expresiones explícitas de las derivadas en (177), nos
da como condición de equilibrio la siguiente ecuación:
SÁT) + R T log ^ + R T = C; T
^ O
W — T(Cp log T - Rlog p + a + R log R);
Si dividimos por RT y pasamos de logaritmos a números, obte­
nemos :
I
C p T ^ W - T ( C p log r + o + g l o g f i ) - / i ( D - g r
____
—
HT
pNo
= K{T),
donde K {T ) es una función de la temperatura únicamente.
La ecuación (181) expresa la siguiente ley:
La concentración de una solución de un gas disuelto en un
líquido a una temperatura dada es proporcional a la presión del
gas por encima de la solución.
Se puede demostrar de manera análoga que si hay una mezcla
de varios gases por encima de un líquido, la concentración de cada
gas en solución es proporcional a su presión parcial en la mezcla
por encima del líquido. La constante de proporcionalidad en cada
caso depende de la temperatura y también de la naturaleza del sol­
vente y del gas particular considerado.
29. La presión de vapor, el punto de ebullición y el punto
de congelación de una solución
La presión de vapor, el punto de ebullición y el punto de,
congelación de una solución no son los mismos que los del solvente
puro. Desde un punto de vista práctico, este hecho es muy impor­
tante, porque, como demostraremos en este parágrafo, las varia­
ciones de los puntos de ebullición y congelación, al menos en las
soluciones diluidas, son proporcionales a las concentraciones mo­
leculares de los solutos. La observación de estas variaciones apor­
ta, por lo tanto, un método muy conveniente para la determinación
de las concentraciones moleculares de la solución.
Haremos la suposición de que los solutos son no volátiles. En
ese caso, el vapor de la solución contendrá solamente solvente
121
puro vaporizado. Además supondremos que, cuando la solución
se congela, se separa solo el solvente puro solidificado, dejando
todo el soluto todavía en solución.
Mediante consideraciones muy simples podemos demostrar
ahora que la presión de vapor para una solución a una tempera­
tura dada es menor que la del solvente puro a la misma tempe­
ratura. Con este objeto consideremos el aparato de la figura 21.
Consiste en un tubo rectangular en el cual el solvente puro y la
solución están separados entre sí en la parte inferior por una
membrana semipermeable en B. Los niveles A y C del solvente
puro y la solución, respectivamente, no se hallan a la misma al­
tura debido a la presión osmótica. El nivel C de la solución será
más elevado. Como la substancia disuelta es no volátil, la región
en el tubo por encima de .A y C estará llena de vapor del solvente
puro solamente. '
En primer lugar esperamos que se establezca el equilibrio;
la presión de vapor en el entorno del menisco A será entonces la
del vapor saturado en equilibrio con la fase líquida y la presión
Vapor de solvente
■z>
Solvente B
Solución
Fig. 21
de vapor en C será la del vapor saturado en equilibrio con una
solución. Es evidente que las presiones en >1 y C no son iguales,
ya que A y C están a diferentes alturas en el vapor. Como la al­
tura de C es mayor que la de A, la presión de vapor en C es menor
que en A·, es decir, que la presión de vapor por encima de la
solución es menor que la presión de vapor por encima del solvente
puro.
Para calcular esta diferencia de presión, ^p, cuantitativa­
mente, observemos que es igual a la presión que ejerce una co­
lumna de vapor de altura h. Si p' es la densidad del vapor y g
la aceleración de la gravedad, tenemos:
Ap = phg.
122
Por otra parte, la presión que ejerce la columna líquida CD
es igual a la presión osmótica P de la solución. Si p es la densidad
del solvente puro, tendremos para la presión osmótica (despre­
ciando la diferencia entre la densidad de la solución y la del sol­
vente puro y también la densidad del vapor comparada con la
del líquido):
P = phg.
Dividiendo la primera ecuación por la segunda, obtenemos;
^
p
^ p'
p'
o también
Ap = pP- = P - ] ,
P
t'o
donde Vq y v ’q son los volúmenes que ocupa un mol de solvente
puro en la fase líquida y en la fase de vapor, respectivamente (es
decir, que Vo y v 'q son inversamente proporcionales a p y p', respec­
tivamente). Reemplazando la presión osmótica P por la expresión
(165), y suponiendo, para simplificar, que hay solo un soluto
presente en la solución, tendremos:
( 182)
¿
Vq N ü
que es la expresión para la diferencia entre la presión de vapor
de la solución y la del solvente puro.
El hecho de que la presión de vapor de una solución sea
menor que la del solvente puro está relacionado con el de que el
punto de ebullición de una solución es mayor que el del solvente
puro. La razón de esto es que el punto de ebullición es la tem­
peratura para la cual la presión de vapor es de una atmósfera.
Clonsideremos un solvente puro en el punto de ebullición; su pre­
sión de vapor es igual a una atmósfera. Si ahora disolvemos
alguna substancia en este solvente, manteniendo constante la tem­
peratura, la presión de vapor caerá por debajo de una atmófera.
Por consiguiente, para llevar nuevamente la presión a su valor
original de una atmósfera, debemos elevar la temperatura de la
solución. Con la ayuda de la ecuación (182) y la ecuación de
Clapeyron podríamos obtener fácilmente una expresión para la
variación del punto de ebullición de una solución. Pero nosotros
calcularemos la disminución de la presión de vapor y el aumento
123
I
en el punto de ebullición de una solución mediante un mètodo
directo.
Consideremos una solución diluida compuesta por N o moles
de solvente y Ni moles de un soluto en equilibrio con el vapor
del solvente puro. Sea N ’o el nùmero de moles del solvente con­
tenidos en la fase vapor. Por (148), (149), (155) y (121), ob­
tenemos para el potencirl termodinàmico
de la solución:
*í>aoi = No(po{T, p) + Ni<pi{T, p) + R TN i log —-,
donde
<Po{T, p) == rio — Tao + pz'o, and
— T(Ti + pvi.
Sea 9'() {T, p) el potencial termodinàmico de un mol de vapor
del solvente. El potencial termodinàmico de los N'o moles de la
fase vapor será entonces;
^vap — N q(Po{T, p) ¡
y el potencial termodinàmico del sistema total es;
^ = ^«, 1 + «ivap = No<PoiT, p) + Ni<pi{T, p) + RTN i log ^
iVo
+
iC ‘
N W
oÌ T
,
p
).
(183)
La condición de equilibrio es que a temperatura y presión
constantes ‘I’ sea un mínimo. Por lo tanto deberá ser d·*· = O para
una transformación infinitesimal isotérmica e isobàrica. Si dNo
moles de solvente son transferidos de la fase vapor a la solución
como resultado de dicha transformación (es decir, si No y N'o
varían en dNo y — dNo, respectivamente), entonces deberá ser:
it i
dNo
dNo
a<i>
lí
dNo
dNo
Reemplazando en esta ecuación las derivadas por sus ex­
presiones explícitas, como han sido calculadas de (183), obtene­
mos:
124
v>o(r, p ) - R T ^ ^ = <po{T,v),
( 184)
<PÁT, v) - <Po{T, v) = R T
Esta ecuación expresa la relación que existe entre la temperatura
y la presión de vapor de nuestra solución.
Sea Po la presión del vapor saturado del solvente puro a la
temperatura T. T y po satisfarán la ecuación (184) si hacemos
Ni = 0 en dicha ecuación, ya que en ese caso no habrá ningún
soluto presente. Así es que:
M T , Po) -
<pUT, P o)
= 0.
(185)
Cuando se disuelven en el solvente Nj, moles del soluto, la
presión p del vapor se convierte en
p = Po + Ap,
donde
es una cantidad pequeña. Desarrollando el primer miem­
bro de (184) en potencias de ^p hasta los términos de primer
orden, tenemos que:
RT
JVo
= m(.T, p.) - vUT, p.) + Ap
[
dpo
dpo
)
Como <Po es el potencial termodinàmico de un mol de solvente puro,
obtenemos de (123) :
d<po{T, Po)
_
------ ---------- — Vq ,
dpo
siendo Vo el volumen de un mol de solvente y, análogamente,
d(Po{T, Po) _
/
dpo
125
r
donde v'o es el volumen de un mol de vapor del solvente puro.
Substituyendo estas expresiones en (186), tenemos:
Ap = -
,«
(18T)
Vo — Vo N o
Como el volumen, v’o de un mol de vapor es mayor que el
volumen Vo de un mol de solvente líquido,
es negativo; esto
significa que la presión de vapor de la solución es más baja que
la del solvente puro. Si Vq es despreciable en comparación con
v'o, como supusimos al obtener la ecuación (182), la ecuación
(187) será idéntica a la (182). (El signo menos significa que la
presión de vapor de la solución es menor que la del solvente
puro.)
Hemos deducido la expresión para el descenso de la presión
de vapor a partir de (184). Con ayuda de la misma ecuación y
por un método análogo al utilizado, podemos calcular también
el cambio en el punto de ebullición de una solución.
Consideremos una solución cuya temperatura es tal que la
presión p de su vapor es igual a una atmósfera. Sea To el punto
de ebullición del solvente puro y T = To
^T el de la solución.
Dado que la presión de vapor en el punto de ebullición es igual
a la presión atmosférica, p, se deduce que la presión de vapor
del solvente puro a la temperatura To es igual a p. Como
= O
para el solvente puro, utilizando la (184) tenemos que:
M , p ) - <pó(To,p) = 0.
(188)
Aplicando (184) a la solución, obtenemos:
1.;
^o(To +
P) ~ Vo(To + AT, p) — R T
Desarrollando el primer miembro de la precedente ecuación
en potencias de AT, sin tener en cuenta los términos de orden
superior al primero, obtenemos, por medio de (188), la siguiente
ecuación:
/3^o(!To, p)
d(p'o{To,p)\ _ 7J7T Ni
----------- •F .·
( ··
11
De (124) tenemos:
d<po{TQ,p)'_
dTo
126
d < p' o ( To , p ) _
dTo
r
donde ao y a'o son las entropías de un mol de solvente en las fases
líquido y vapor, respectivamente. De las dos ecuaciones que an­
teceden, obtenemos ahora:
ATlaó - ao} = R T o ~ \
(139)
iVo
Sea A el calor de vaporización de un mol de solvente. Si se
vaporiza un mol de solvente a la temperatura de ebullición, T q,
la cantidad de calor absorbida es igual a A, y — es la variación
To
de la entropía. Por lo tanto,
/
A
ao — ao — -ffr·
■í o
Substituyendo ésta en la ecuación (189), obtenemos:
AT.= ^ ^ \
A
(190)
No
Ésta es la expresión de la diferencia entre el punto de ebu­
llición de la solución y el del solvente puro. Como AT > O, el
punto de ebullición de la solución es más elevado que el del sol­
vente puro. Vemos también, por la ecuación, que la variación
del punto de ebullición es proporcional a la concentración mo­
lecular de la solución.
Para dar un ejemplo, aplicaremos la ecuación que antecede
a una solución normal de una substancia en agua. Para una so­
lución de ese tipo se tiene:
Ni = 1 ;
No = -------- ;
18
R — 1,986 calorías;
= 540 'X 18 calorías ;
To = 373,1°.
(En la ecuación [190] tanto R como A pueden expresarse en ca­
lorías, ya que, como es obvio, su relación carece de dimensiones.)
Substituyendo estos valores en la ecuación (190) obtenemos:
AT = 0,51 grados
Podemos utilizar esta misma fórmula (190) para calcular có­
mo varía el punto de congelación de una solución. La única dife­
rencia consiste en que, en lugar de tener una fase vapor, tenemos
una fase sólida. En este caso A representa el calor absorbido por
127
referencia O .introducido en el parágrafo 12; esto nos permitirá
establecer la entropía del estado de referencia igual a cero.
La entropía de cualquier estado A del sistema queda ahora
definida, incluyendo la constante aditiva, por medio de la integral:
S(A)
l'-O T ’
(192)
donde la integral se toma a lo largo de una transformación re­
versible desde un estado cualquiera a T = O (límite inferior) hasta
el estado A.
En este libro tomaremos el teorema de Nemst como un pos­
tulado. Algunas palabras con respecto a su base teórica servirán,
sin embargo, para demostrar su plausibilidad.
Hemos visto que el estado termodinàmico de un sistema no
es un estado rigurosamente definido del sistema, ya que corres­
ponde a un gran número de estados dinámicos. Esta consideración
condujo a la relación de Boitzmann (75) :
S = A: log ir,
donde tt representa la probabilidad del estado. Rigurosamenté ha­
blando, 7T no es la probabilidad del estado, sino, en realidad, el
número de estados dinámicos que corresponden al estado termodinámico dado. Esto aparece, en principio, como causa de una
seria dificultad, ya que a un estado termodinàmico le correspon­
den un número infinito de estados dinámicos. Esta dificultad se
salva en la mecánica estadística clásica mediante el siguiente ar­
tificio;
Los estados dinámicos de un sistema forman un arreglo de
00
elementos, donde f es el número de grados de libertad del
sistema; cada estado puede, por lo tanto, representarse por un
punto en un espacio 2/-dimensional, que es el llamado espacio
de las fases del sistema. En lugar de una representación exacta
del estado dinámico, que podría lograrse señalando la posición
precisa del punto que representa a dicho estado en el espacio de
las fases, se introduce la siguiente representación aproximada.
Se divide el espacio de las fases en un número de celdas muy
pequeñas que tienen todas el mismo hiper-volumen t. El estado
queda entonces caracterizado especificando a qué celda pertenece
el punto que representa a dicho estado. De esta manera, los esta­
dos cuyos puntos representativos se hallan en una misma celda
no son considerados como estados diferentes. Esta representación
del estado de un sistema seria evidentemente exacta si las celdas
fuesen infinitesimales.
La representación celular de los estados dinámicos de un sis­
tema introduce, en el concepto del estado de un sistema, una
discontinuidad que nos permite calcular tt mediante los métodos
del análisis combinatorio, y por lo tanto, con ayuda de la relación
de Boltzmann, dar una definición estadística de la entropía. De­
bemos advertir, sin embargo, que el valor de tt, y por consiguiente
el valor de la entropía, depende de la elección arbitraria del ta­
maño de las celdas. Si hacemos tender a cero el volumen de la
celda, vemos que tanto S como tt se hacen infinitos. Podemos
demostrar, sin embargo, que si t varía, tt se altera en un factor;
pero de la relación de Boltzmann se deduce que un factor inde­
terminado en TT hace aparecer una constante aditiva indetermi­
nada en S. Vemos, a través de las consideraciones que anteceden,
que la mecánica estadística clásica no puede conducir a la deter­
minación de la constante de entropía.
La arbitrariedad asociada con tt, y por lo ^ ^ to con la en­
tropía, puede ser suprimida en el tratamiento clásico mediante
la aplicación de los principios de la teoría cuántica. Esto se debe
a que la teoría cuántica introduce muy naturalmente una discon­
tinuidad en la definición del estado dinámico de un sistema (los
estados cuánticos discretos) sin tener que hacer uso de la arbitra­
ria división del espacio de las fases en celdas. Podemos demostrar
que esta discontinuidad es equivalente, para fines estadísticos, a
la división del espacio de las fases en celdas que tienen un hipervolumen igual a W, en donde h es la constante de Planck
( h = ‘ 6,55 iX
cm- g seg-^) y / es el número de grados de li­
bertad del sistema. Podemos tener en cuenta aquí, sin entrar en
detalles, que sobrepasan los alcances de este libro, que en una teoría
estadística basada en forma consistente en la teoría cuántica toda
indeterminación en la definición de ir, y, por consiguiente, en la
definición de entropía, desaparece.
De acuerdo con la relación de Boltzmann, el valor de tt que
corresponde a 5 = 0 es ir = 1. Interpretado estadísticamente, el
teorema de Nernst afirma que al estado termodinàmico de un
sistema en el cero absoluto, le corresponde solamente u n estado
dinámico, a saber, el estado de mínima energía compatible con la
estructura cristalina dada o el estado de agregg¡ción del sistema.
Las únicas circunstancias en las cuales el teorema de Nernst
puede estar equivocado son aquéllas en que existen muchos esta­
dos dinámicos de mínima energía. Pero, aun en este caso, el
número de tales estados debe ser enormemente grande ^ para que
^ Del orden de e^, donde N es el núm ero de m oléculas presentes en
el sistem a.
131
la desviación del teorema sea apreciabU-. Aunque teóricamente no
es imposible concebir este tipo de sistema, es extremadamente difí­
cil que tales sistemas existan realmente en la naturaleza. Podemos
suponer entonces que el teorema de Nernst es generalmente válido.
Vamos a estudiar ahora algunas de las consecuencias de dicho
teorema.
31. El teorema de Nemst aplicado a sólidos
Consideremos un cuerpo sólido calentado (a presión cons­
tante, por ejemplo) hasta que su temperatura se eleve desde el
cero absoluto hasta un cierto valor T. Sea C(T) su capacidad
térmica (a presión constante) cuando su temperatura es T. En
ese caso, si su temperatura varía en un dT, el cuerpo absorberá
una cantidad de calor dQ == C{T)dT. La entropía del cuerpo a
la temperatura T estará por lo tanto dada (ver ecuación [192])
por:
S
dT.
(193)
De la ecuación (193) obtenemos la primera consecuencia del
teorema de Nernst: observamos que si la capacidad térmica, C(0),
en el cero absoluto fuese distinta de cero, la integral (193) sería
diferente en el límite inferior. Debemos tener entonces:
C(0) = 0.
(194)
Este resultado concuerda con las experiencias sobre los calores es­
pecíficos de los sólidos.
Nos limitaremos aquí, para simplificar, a la consideración
de elementos químicos sólidos, y efectuaremos los cálculos para
un átomo gramo del elemento. La figura 22 es una representación
Fig. 22
132
gráfica de la forma generai en que los calores atómicos de los
sólidos dependen de la temperatura, como ha sido comprobado em­
píricamente. Podemos ver en la figura que el calor atómico real­
mente se anula en el cero absoluto. A temperaturas más elevadas,
C{T) se aproxima a un valor límite que es aproximadamente el
mismo para todos los sólidos y que se halla muy próximo al valor
3ñ. Como este valor límite se alcanza prácticamente a tempera
tura ambiente, este resultado es una expresión de la conocida ley
de Dulong y Petit, cuyo enunciado es el siguiente:
A la temperatura ambiente, todos los elementos sólidos tiemen
el mismo calor atómico, que es igual a 3R (es decir, que el pro­
ducto, calor específico po-r peso atómico es el wÁsmo para todos los
sólidos y es igual a 3R).
Debye dedujo, basándose en la teoría cuántica, una fórmula
teórica para los calores específicos de los elementos sólidos, que
está muy de acuerdo con los resultados experimentales. La ex­
presión de Debye puede escribirse así:
C(T) =
Í195)
donde s es una constante característica de las substancias, que
tiene las dimensiones de una temperatura; es la llamada tempe­
ratura de Debye. D representa la siguiente función:
1
o
D(í) = 12í· Jo
í ' 4 ^ - - ¡T i^ ·
e* — 1
—1
<19«)
Dado que D(é) se aproxima al límite 1 para valores grandes
de 4', de (195) surge que el calor atómico para altas temperaturas
tiende al límite 3ñ tal como lo requiere la ley de Dulong y Petit.
Para valores pequeños de ¿ podemos reemplazar el límite su­
perior de la integral en (196) por infinito, y despreciar el segundo
término en esa expresión, ya que dicho término se transforma en
un infinitésimo de orden muy elevado para valores infinitesima­
les de
Por lo tanto, para | O obtenemos:
D (0 -> 12^ Jo
r 4 ^— 1 = ^5 í'·
133
r;'·
De esta expresión asintótica para D (¿) obtenemos la si­
guiente expresión para el calor atómico en el límite de las bajas
temperaturas :
A
(198)
C(T)
«...
Í'
■
Aquí vemos que a bajas temperaturas el calor atómico es propor­
cional al cubo de la temperatura. Esta consecuencia de la teoría
de Debye concuerda con los resultados experimentales.
Haciendo uso de la fórmula de Debye podemos calcular la
entropía de un átomo gramo de nuestra substancia substituyendo
(195) en (193). Vemos así que:
= 3« f
S=
« f ) f .
(199)
Reemplazando en (199) D($) por su expresión explícita, com­
probamos que: ^
II·
= 3i21ogr + 4 i2 - 3 i2 1 o g e + · · · ,
í200)
2 Se utilizan las sigu ien tes fórm ulas integrales:
o, intercambiando el orden de integración en la inteíjral doble e introduciendo e/t como
nueva variable en la segunda integral, tenemos:
/*“
df
3^dx
f ‘" »
/'°°
dx
/"* ■,
f
<a
Jo
«
^
Para valores grandes d» w, ob ten em os la sigu ien te expresión asin tótica:
H·
/■
‘iii
f,
L·
134
dx
Esta última fórmula es válida para T » O, o sea dentro de la región
de temperaturas para las cuales se cumple la ley de Dulong y Petit.
Veremos ahora, teniendo en cuenta el teorema de Nemst, la
transformación del estado cristalino de un sólido en otro. Como
ejemplo tomaremos la transformación del estaño gris en blanco.
El estaño gris es estable a bajas temperaturas, mientras que el
blanco lo es a altas temperaturas. La temperatura de transición,
To, es igual a 19° C ó 292" K.
La transformación del estaño de una de estas formas alotró­
picas a la otra es análoga en muchos aspectos a la fusión de un
sólido. Por ejemplo, el estaño absorbe una cantidad de calor al
pasar de su forma gris a la blanca. Este calor de transformación,
Q, es igual a 535 calorías por átomo gramo a la temperatura de
transición.
Aunque la forma estable del estaño gris se halla por debajo
de la temperatura de transición, el estaño blanco puede existir en
forma lábil hasta las temperaturas más bajas. Por lo tanto, es po­
sible medir los calores específicos del estaño gris como del blanco
a lo largo de la región que comprende desde las temperaturas más
bajas hasta la temperatura de transición. Los calores atómicos de
ambas formas son distintos; el calor atómico del estaño gris a una
temperatura dada es menor que el del blanco a la misma tempe­
ratura.
La transformación del estaño blemco en gris a t^peraturas
por debajo de la temperatura de transición no es reversible. (Como
la forma gris es estable por debajo de la temperatura de transi­
ción, una transformación espontánea puede ocurrir solamente de
la forma blanca a la gris.) A la temperatura de transición, sin em­
bargo, aqutella transformación es reversible.
Si Si (To) y 5o (T q) son las entropías a la temperatura de
transición de un átomo gramo de estaño gris y blanco, respecti­
vamente, aplicando (69) a la transformación isotérmica reversi­
ble del estaño gris en blanco se obtiene:
blan co
s m
- S¿To) = í .
y gris
P
Jo
=
io
Í201) .
Indicando los calores atómicos del estaño gris y blanco por Ci (T)
y CaíT), respectivamente, y haciendo uso de la ecuación (193),
podremos expresar Si (Tq) y S^ (Tq) de la siguiente forma:
Si(To) =
S,(To) =
(202)
De este modo obtenemos de (201) la ecuación:
135
Q=
L·
(203)
la cual expresa el calor de transformación, Q, del proceso en tér­
minos de la temperatura de transición T y de los calores atómicos
de las dos formas de estaño.
Con el objeto de comprobar la validez de la ecuación (203),
efectuarenws las integraciones indicadas numéricamente. Los re­
sultados de esas integraciones numéricas son:
grados’
r
T
Jo
m
cal.
dT = 10.53
T
grados'
Como To = 292, obtenemos reemplazando estos valores en
(203):
Q = 292 (12,30 — 10,53) = 517 calorías.
La aceptable concordancia entre este valor y el valor expe­
rimental, Q = 535 calorías, puede tomarse como una fuerte evi­
dencia en apoyo del teorema de Nernst. La pequeña diferencia
entre ambos valores puede atribuirse a errores experimentales.
32. La constante de entropía de los gases
En el parágrafo 14 hemos calculado la entropía de un mol
de un gas ideal (ver ecuación [86]) y hemos visto que:
S = Cv log T + ñ log V + a.
La constante aditiva indeterminada o que aparece en esta expre­
sión es la constante de entropía del gas.
Si fuese posible aplicar directamente el teorema de Nernst
a la fórmula (86), podríamos pensar en la determinación de a
mediante la condición de que la entropía S debe anularse para
T = 0. Sin embargo, si lo intentamos, vemos que el término Cy
log T del segundo miembro de (86) se hace infinito, y obtenemos
entonces para la constante de entropía un valor infinito.
Esta aparente falla del teorema de Nernst para el caso de los
gases ideales, debe atribuirse al hecho de haber supuesto que el
calor específico Cy de un gas ideal es una constante. Hemos de­
mostrado ya, al comienzo del parágrafo precedente, que esta hipó­
tesis es incompatible con el teorema de Nernst.
136
Para allanar esta dificultad podríamos apoyarnos en el hecho
de que ninguna substancia real se comporta, ni aun aproximada­
mente, como un gas ideal en la vecindad del cero absoluto; a tem­
peraturas suficientemente bajas todos los gases se condensan. Es
por lo tanto físicamente ilícito aplicar la (86) a un gas en las
proximidades de !T = 0.
Pero apartándonos de esta consideración, la mecánica cuán­
tica muestra que, aun para el caso de un gas ideal (definido como
un gas cuyas moléculas tienen un tamaño despreciable y no ínteractúan), el calor específico decrece al disminuir la temperatura,
y llega a anularse en las cercanías de T = 0. Es por eso que, aun
para un gas ideal como el defiínido anteriormente, la ecuación (86)
puede aplicarse únicamente si la temperatura no es demasiado
baja.
Mediante métodos estadísticos y también por aplicación di­
recta del teorema de Nernst es posible calcular la entropía de un
gas ideal para todas las temperaturas. En el límite de las altas
temperaturas la entropía toma la forma (86) con la constante a
expresada en función del peso molecular y de las otras constantes
moleculares del gas, en lugar de estar indeterminada.
El caso más simple es el de un gas monoatómico, para el cual
la entropía de un mol está-dada por:
(27rMR)^coe^
- log r + log F + log -
(204)
en donde M es el peso atómico; h la constante de Planck (h = 6,55
X 10·"^·^ unidades C G S ); A el número de Avogadro (A = 6,03
X 10‘ ^); y w es un pequeño entero, denominado el peso estad^ístico del estado base del átomo. El valor de « para diferentes áto­
mos se obtiene teniendo en cuenta la teoría cuántica. Para todos
los ejemplos considerados aquí, daremos el valor de m. e es la base
de los logaritmos naturales.
La fórmula (204) fue obtenida por Tetrode y Sackur. De-'
mostraremos ahora que dicha fórmula puede expresarse en la forma
de (86) teniendo en cuenta los valores dados en (34). Obtenemos
entonces para la constante de entropía de un mol de gas monoató­
mico la expresión:
„
,
a = K log
(2TrM/2)V
= ñ ^ - 5 . 6 5 + I log M + log « y
i
(205)
137
Podemos también escribir la entropía de un gas ideal monoató­
mico en la forma correspondiente a (87):
S = R 2 log T - log p + log
( 2 7 r M fR L ·^
(206)
i
{·
1f
Ì
l
Como no podemos dar en este libro una demostración de
estas fórmulas, nos limitaremos a presentar algunos ejemplos de
su aplicación. Como primer ejemplo consideraremos el problema
de calcular la presión de vapor de una substancia sólida mo­
noatómica.
Sea p la presión de vapor de la substancia a la temperatura
T. Manteniendo la temperatura (y la presión constante e incre­
mentando lentamente el volumen, vaporizamos un mol de la
substancia. En el transcurso de este proceso el cuerpo absorbe del
medio ambiente xma cantidad de calor. A, igual al calor de vapo­
rización (por mol y no por gramo). Como el proceso de vaporiza­
ción de im mol de la substancia se efectúa en forma reversible,
la variación de la entropía durante la transformación es:
Svapar
<Ss¿llrfo------ .
Haciendo uso de la expresión aproximada (200) de la entropía
del sólido y de la fórmula (206) de la entropía del vapor obtenemos:
- ZR log T
- 4i2 + 3i2 log 0 -=
y pasando de logaritmos a números:
(207)
V=
e^h^A*
V f
Comparemos esta fórmula con la (98), obtenida de la ecuación
de Clapeyron. El factor X/ \ / T aparece en (207) como resultado
de haber tenido en cuenta la dependencia de la temperatura, del
calor de vaporización. Vemos que el factor de proporcionalidad,
indeterminado en (98), ha sido determinado completamente en
138
(207) mediante el uso del teorema de Nemst y la fórmula de
Sackur-Tetrode para la entropía de un gas.
No podemos generalizar el uso de la fórmula (207), ya que
en muchos casos debemos ocuparnos de la vaporización de un
líquido y no de un sólido. Como ejemplo de la vaporización de un
líquido, consideraremos la vaporización de un mol de mercurio, ya
que el vapor de este elemento es monoatómico.
El punto de ebullición del mercurio es de 630® K, Esto sig­
nifica .que la presión de vapor del vapor de mercurio saturado a
630" K es igual a una atmósfera.
Vamos a calcular ahora la entropía de un mol de mercurio
8 7* = 630° K y j) = 1 atmófera, utilizando dos métodos diferentes
y comparando luego los resultados.
Método 1. La fórmula (206) de Sackur-Tetrode aplicada a
nuestro caso (el peso atómico del mercurio es 200,6) da:
S = 191 X 10^
Método 2. Partimos de un mol de mercurio sólido en el
cero absoluto. Su entropía, según el teorema de Nemst, es cero.
Calentamos entonces ese mol de mercurio manteniendo la presión
igual a una atmósfera, hasta que su temperatura alcanza el pvmto
de fusión, Tr„„trir. = 234,2° K. Durante este proceso la entropía
del mercurio crece; su valor para T = 234,2“ K puede ser calculado
mediante la (193) :
^234,2
SsMido (2 3 4 ,2 )- /
^ d T ,
Jo
·*
donde C (T ) representa el calor atómico del mercurio a presión
constante. Esta integral puede ser calculada numéricamente ha­
ciendo uso de los valores de C(T) determinados experimental­
mente. De esa manera obtenemos:
Ss6iido (234,2) =59,9 X lO ^
Fundimos ahora el mol de mercurio a la presión atmosférica.
Durante este proceso el cuerpo absorbe en forma reversible una
cantidad, de calor igual al calor de fusión de un mol de mercurio
(2.330 X lO’^ erg/mol). La variación de entropía resultante se
obtiene dividiendo el calor de fusión por el punto de fusión; es de­
cir que la variación de entropía es igual a
2.330 X 10V234,2 = 9,9 X 10^
1 *7 0
La entropía total del mol de mercurio es ahora;
Sifqmao (234,2) = 59,9 X 10^ + 9,9 XlO^ = 69,8 X 10^
Luego calentamos el mercurio líquido y elevamos su tempe­
ratura desde el punto de fusión al de ebullición. Durante este
proceso de entropía cambia en la cantidad.
/•630
m
/
Siícuido (630“) — Snauido (234,2°)
y 234,2 Tí
dT,
donde Ci(T) es el calor atómico a presión constante. Podemos
evaluar numéricamente esta integral haciendo uso de los valores
experimentales de C ;(T ). Su valor es igual a 26,2 X 10'. Sumando
este valor al de la entropía del mercurio líquido en el punto de
fusión, obtenemos :
s
It' »
líquido (630°) ^ 69,8
X
10' + 26,2
X
10^ = 96,0 X 10^
Finalmente hacemos que la vaporización del mercurio se
efectúe a la presión atmosférica. (3omo resultado de esto, el
mercurio a la temperatura T = 630° absorbe una cantidad de
calor igual al calor de vaporización de un 'mol de mercurio
(59.300 X lO’^ ergios/mol). La variación de entropía es, por lo
tanto, igual a 59.300 X 10V630 — 94 X 10^. Obtenemos así final­
mente para la entropía del mol de vapor de mercurio a la tem­
peratura de ebullición el valor;
: 96
X
10^ + 94
X
10^ = 190
X
10^
Este resultado está en excelente concordancia con el valor obte­
nido directamente con la fórmula de Sackur-Tetrode, y puede
considerarse como una demostración experimental de la expresión
de la entropía de un gas monoatómico. Cálculos similares han sido
efectuados para el argón y el carbón, con resultados altamente
satisfactorios.
33. Ionización térmica de un gas; efecto termoiònico
En el capítulo VI hemos establecido la ley de acción de masas
(ecuación [139]) para el equilibwio químico de sistemas en fase
gaseosa. El coeficiente constante (el factor que no contiene a
la temperatura) del primer miembro de (139) contiene las cons­
tantes de entropía de los gases que participan en la reacción. El
L ·l
140
conocimiento de las constantes de entropía nos permite, por lo
tanto, calcular este coeficiente en forma completa.
Como solo hemos dado la expresión de la constante de entro­
pía de un gas para gases monoatómicos, debemos elegir, a título
de ejemplo, una reacción en la cual solamente intervengan gases
monoatómicos. Es evidente que ninguna reacción en química
puede tener estas características. Consideraremos, por consiguien­
te, el siguiente proceso no químico.
Cuando un gas, como por ejemplo, el vapor de un álcali, se
calienta hasta llegar a una temperatura muy elevada, algunos de
sus átomos se ionizan, es decir, pierden uno de sus electrones y
se transforman en iones. Si entonces designamos mediante Na,
Na* y e a los átomos de sodio, iones de sodio y electrones, res­
pectivamente, el proceso estará representado por la reacción:
Na
Na·" -f e
(208)
Se observa que, cualquiera sea la temperatura dada, esta
reacción de ionización alcanza un estado de equilibrio térmico
análogo al equilibrio químico de las reacciones químicas corrientes.
En el vapor de sodio a muy altas temperaturas encontramos
una mezcla de tres gases diferentes: sodio neutro, es decir. Na,
con una concentración [N a] ; iones de sodio, Na^, con una concen­
tración [Na^], y un gas de electrones (gas compuesto de electrones
libres) que tiene una concentración [e].
Cada una de estas tres substancias se comporta como un gas
monoatómico; podemos, por consiguiente, aplicar los resultados
generales, en particular la ecuación (139) de la teoría del equili­
brio químico de sistemas en fase gaseosa al proceso de ioniza­
ción (208). ·
Como todos los gases de la mezcla son monoatómicos, debemos
usar la primera de las expresiones (34) para los calores molecu­
lares de los gases. Las constantes de entropía pueden ser determi­
nadas mediante la ecuación (205), y los pesos estadísticos w son
iguales a 2, 1, y 2 para el sodio neutro, iones de sodio y electrones,
respectivamente. Tomamos el valor M = 23 como peso atómico
del sodio, y despreciando la pequeña diferencia entre las masas
de los átomos de sodio y los iones de sodio podemos asignar
también valor M al peso atómico de los iones de sodio. El peso
atómico de los electrones (es decir, la masa de los electrones divi­
dida por — de la masa de oxígeno) es M,· = -------- . Finalmente,
16
1.830
designaremos W (W = 4,91 X 10*’- erg/mol) a la energía nece­
saria para ionizar todos los átomos de un mol de vapor de sodio.
Tenemos entonces:
141
i?
Ir,'·
' ^ n i j W j ---^ 7 l¡ W¡ = Wiones + Wclectrones---- Watomoa = W.
§
*^7
fet*·.
Haciendo todas las substituciones necesarias en la ecuación
(139), obtenemos finalrrjente, como condición de equilibrio tér­
mico para la ionización térmica del vapor de sodio, la siguiente
ecuación:
t
l¡
INal _
[Na+llcj
1,'A'
í·
Esta fórmula puede ser expresada en forma más conveniente
de la siguiente manera: sea x el grado de ionización, es decir,
la fracción de átomos ionizados:
i
INaj + [Na+j’
y sea t í = [Na] + [Na+] la concentración totai de sodio (áto­
mos + iones). Será entonces:
[Na+1 = iix;
[Na] = n(l ~ x).
Como es obvio que por cada ion de sodio hay presènte un electrón,
se tiene :
[e] = [Na+] = nx,
í;
i-
y por último obtenemos :
i.
n
''l-X
rn-2 nT
^ "
3
= 3.9 X 10"®
L
II,;.
Ito
Br
I;
26,000
10
^ .
(209)
El grado de ionización puede calcularse mediante esta fórmula.
La ecuación (209), obtenida por M. N. Saha, ha tenido im­
portantes aplicaciones en la física de las atmósferas estelares,
Como una aplicación más de la fórmula de Sackur-Tetrode,
vamos a obtener ahora la expresión de la densidad de un gas de
electrones que está en equilibrio con una superficie metálica calíente. Cuando un metal se calienta hasta alcanzar una tempe­
ratura suficientemente elevada, empieza a emitir una corriente
continua de electroner,. Si calentamos un bloque de metal que
contiene una cavidad, los electrones emitidos por el metal irán
142
llenando la cavidad hasta alcanzar un estado de equilibrio, en el
cual la cantidad de electrones reabsorbidos por el metal en la
unidad de tiempo será igual a la de los emitidos. Nos propone­
mos calcular la concentración de equilibrio de los electrones den­
tro de la cavidad como una función de la temperatura.
Sea N el número de moles de electrones que están dentro de
la cavidad de volumen V. La entropía de estos electrones se obtiene
multiplicando la expresión (204) por N y reemplazando V por V/N ,
ya que V / N es el volumen que ocupa im mol del gas de electrones.
Mediante (34) y (29), obtenemos para la energía de los electrones:
U = N i ^ R T + W)
donde W representa la energía necesaria para extraer vm mol de
electrones del metal.
La expresión de la energía libre de un gas de electrones es
entonces ;
Fei = N i ^ R T + W) - N R T
+ log
(2irM.R)^ 2e^
h^A*
donde entendemos Me -- --------- --- peso atómico de los electro1.830
nes y mpara los electrones = 2.
La energía libre F de todo el sistema es la suma de la anterior
expresión y la energía libre Fu del metal:
F = Fm + N ^ R T + W - R T
I log T + log F - log iV
+ log
2{2wM,R)^
■ÍJ
(210)·
La condición de equilibrio es que F sea un mínimo para una
temperatura y volumen dados. Si suponemos que F « es indepen­
diente ® de N, obtenemos:
® La base experim ental que perm ite hacer e sta suposición es que los
electrones que están dentro del m etal no inciden sobre el calor específico
del m ism o: el calor específico queda com pletam ente explicado por el m ovi­
m iento de los átom os. Para una ju stificación m ás rigurosa de nuestra hip ó­
tesis, ver cualquier tratado sobre teoría de los m etales.
143
r
. i
<
4·.
^logT + l o g F - l o g N
(<*
a
.-VJ ·
2{27rM,
+ log
h^A*
81
+ RT.
L ·.
Pasando de logaritmos a números, obtenemos la ecuación:
r
N
V
^
2 (2 T rM .fí) ^ y |
^
7
g g
^
jq -9
y f
^ 2 1 1 )
h^A*
que nos permite conocer la concentración del gas de electrones
dentro de la cavidad.
Problem as
1. Calcular el grado de disociación del vapor de sodio a una tem pe­
ratura de 4.000*^ií y una presión de 1 cm de m ercurio. (Tener en cu en ta no
solam ente la presión debida a los átom os de sodio, sino tam bién la contribu­
ción de los iones y electrones.)
2. E ncontrar la relación en tre la tem peratura 6 de D ebye y la tem p e­
ratura para la cual el calor atóm ico de un elem en to sólido es igual a 3 ñ /2 .
(A plicar m étod os gráficos o nu m éricos.)
144
r
BIBLIOGRAFÍA
La bibliografía sobre term odinám ica es m u y extensa. A continuación
se m encionan solam en te algunos títu lo s representativos, agrupados según las
orientaciones particulares con q u e se ha desarrollado el tem a.
A) Textos para el estu d ian te de ciencia.
Planck, M., T reatise on T h e rm o d y n a m ic s (3* ed ición ), N u eva York, D over
P ublications, Inc., 1945.
Sears, F. W ., T h e rm o d yn a m ic s, th e K in e tic T heo ry of G ases a n d S t a t i s ­
tical M echanics (2 · ed ición ), M assachu setts, A d dison -W esley Publishing
Co., Inc., R eading, 1953. H ay. una traducción castellana, coni el títu lo
Introducción a la term od in á m ica , teo ria cin ética d e los g a se s y 'mecánica
estadística, Barcelona, R everté S. A., 1959.
Isnardi, T., Term odinám ica, B uenos Aires, E diciones C ientíficas Nfkbla,
1964.
B) Textos para e stu d ia n tes de ingeniería.
Lee, J. F., y Sears, F. W ., T h e rm o d y n a m ic s (2 ’ ed ición ), M assachu setts,
A ddison-W esley Publishing Co., Inc., Reading, 1963.
Em swiller, J. E., T h e rm o d yn a m ic s (5 ' edición, revisado por F. L.
Sch w artz), N u eva York, M cGraw-Hill Book Co., Inc., 1943.
C) Textos avanzados.
Epstein, P. S., T ex tb o o k of T herm od yn am ics, N u eva York, J. W iley and
Sons, Inc., 1957.
G uggenheim , E. A., T h erm o dyn am ics, an A d v a n c e d T re a tm e n t fo r C he­
m is ts a n d P h y sic ists (3* e d ició n ), A m sterdam , North H olland Publishing
Company, 1958.
D) Tratados sobre la fun dam entación estadística de la term odinám ica.
Tolman, R. C., The Principies of S ta tistic a l Mechanics, Londres, OxfordClarendon Press, 1938.
Landau. L. D., y Lifshitz, E. M., S ta tistic a l Physics, Londres, Pergam on
Press, 1958. S e espera la aparición de u n a traducción españ ola en breve.
Morse, P, M., T herm al Physics, N ueva York, W. A. Benjam in, Inc., 1965.
145
ó*.'·
ÍN D I C E
A L FA B ÉT IC O
acción de m asas,
c o n sta n te de, 101;
ley de,
para el equilibrio en fase gaseosa,
92, 99;
para soluciones, 117;
prueba cin ética, 92
acidez de un a solución, 117, 118
aisladores térm icos, 15
A vogadro, 9;
núm ero de, 54
Boltzm ann, IX, 53, 130;
co n sta n te de, 54
caja de reacción de V an ’t Hoff, 93
calor,
atóm ico, 20, 133;
d e fusión, 102, 103;
d e reacción, 102, 103;
de transform ación d e fa ses sólidas,
135;
de vaporización, 63;
específico, 20;
a b ajas tem peraturas, 131, 132,
133;
de un g a s ideal, 22;
de un sólid o a b a ja s tem peratu­
ras, 133, 134;
fórm ula d e D eb ye para el, 133,
134;
tem peraturas, 133, 134
fu en tes de, 28
laten te, 62-63, 127;
m olecular, 20;
unidad de, 16, 17, 18
trabajo y analogía entre, 13, 14
caloría, 16
capacidad térm ica, 19
celda electrolítica reversible, 87
cero, absoluto, 8
ciclo/s, 7
de Carnot, 30
eficiencia del, 33;
propiedades del, 43;
reversibles, 31, 33, 34
Clapeyron, ecu ación de, 59, 63, 64, 78
Q ausius, p ostulado de, 29
com ponentes de -an sistem a, 80-83
com presibilidad,
adiabática, 24. 25, 26, 30, 31;
d e u n liquido, 60, 61
isotérm ica, 30, 31
condicion es de equilibrio, 52, 53, 75,
78
conservación de la energía,
para sistem as term odinám icos, 14,
16;
principio de, 11
constan te /s ,
a d itiv a s arbitrarias,
d e energía, 12, 13, 14;
d e entropía, 49, 129, 136
de Boltzm ann, 54;
de los gases, 8-9;
de Planck, 131
contenido quím ico de un a fase, 80-83
continuidad de im estado, 59, 61, 66,
67
D ebye, 133
fórm ula d e lo s calores específicos,
133,134;
tem peratura de, 133
densidad de un g a s ideal, 9
descenso,
d e la presión d e vap or d e un a so ­
lución, 125;
del pu nto de congelación, 121, 127,
128
descripción de u n a fase, 80-81
disociación de un so lu to en una solu ­
ción, 113, 114, 117, 118
distribución de un soluto,
en tre dos fases líquidas, 118, 119;
en tre un a fase gaseosa y otra lí­
quida, 120, 121
Dulong y P etit, le y de, 133
ecuación,
adiabática,
para un gas de Van der W aals,
71;
para un gas ideal, 25;
de Clapeyron, 59, 63, 64, 78;
de estado, 2
147
<η
•r
ir
vf.
I
Ifc-
Í
'4.
m
de un gas de V an der W aals, 65;
de un gas ideal, 9
de los estad os correspondientes, 69
efecto,
de la presión,
sobre el equilibrio quím ico, 103,·
104;
sobre el punto de congelación del
agua, 64
de la tem peratura sobre, el eq u ili­
brio quím ico, 103, 104;
Joule, 88;
term oiònico, 140-144
eficiencia d e una m áquina térm ica, 33
electrólitos en solución, 128
energía,
conservación de la, 11, 14, 16;
con stan te aditiva de, 13, 14;
definición,
para sistem as dinám icos, 12;
para sistem as term odinám icos, 15
de un gas en el cero absoluto, 22;
de un gas de Van der W aals, 70;
de un gas ideal, 22
libre, 72, 73
de una solución, 109;
de un gas ideal, 77;
parcial, 99;
y condiciones de equilibrio, 74,
75;
entropía, 43, 45, 129, 130, 134;
absoluta, 129;
aditividad, 49;
com o diferencial exacta, 56;
constan te de, 49, 129, 136, 137;
definición, 47;
de un gas de Van der W aals, 70;
d e un gas ideal, 57, 58, 137;
de un sólido, 134;
interpretación estadística, 53 - 54,
131:
parcial, 99, 100
equilibrio,
cin ético de las reacciones, 92;
condiciones d€^, 53, 54, 74, 78;
con stan tes de, 92, 99, 101, 121;
de líquido y sólido, 59, 60, 85, 86;
de líquido y vapor, 59, 60, 85, 86;
d e sólido y vapor, 85, 86;
de un com ponente en dos fases,
118, 119, 120, 121;
equilibrio,
en sistem as gaseosos, 91, 101; '
en soluciones, 115
estados de, 4, 47, 48;
equivalencia entre la tem peratura del
148
term óm etro de gas y la tem pera­
tura term odinám ica absoluta, 39,
40, 41
e sta d o /s,
correspon dien tes, ecuación de los,
69;
de entropía cero, 129, 130, 131;
de referencia, 47
para la energía, 12;
para la entropía, 47
ecuación de, 2;
term odinàm ico de u n sistem a, 1, 3
exp an sión ad iab ática de un gas, 25,
27, 30, 32
experim en to de Joule, 20, 21
expresión diferencial de la primera
ley, 18. 19
fa se /s,
contenido quím ico, 80, 82;
espacio de las, 130;
regla de las, 85
fluido qu ím icam en te hom ogéneo, 1
gas perfecto o ideal, 8-10;
energía, 22
libre, 77
entropía, 58, 137;
presión de un, 8, 9, 10;
trabajo efectu ad o por un, 9;
transform ación adiabática, 24
G ay-Lussac, 9
Gibbs, IX, 85
grados d e libertad o variabilidad de
u n sistem a, 84-85
H elm holtz, 89, 102
ecu ación de, 89
hidrólisis, 117, 118
inflexión, punto de, 61, 65
interpretación,
cin ética de la presión osm ótica, 113,
114;
estad ística de la entropía,-· 53, 106
ionización térm ica, 140, 142,
de un gas, 140, 142,
isocora d e V an ’t Hoff, 76, 89,
aplicada a la celda eléctrica, 88, 89
iso term a /s,
crítica, 61, 65;
de un vapor saturado, 59
isotérm ica,
com presión y expansión, 31, 32;
crítica, 61, 65;
transform ación, 8
Joule, efecto, 88
K elvin, postulado de, 29
Le C hatelier, principio de, 101, 103
aplicado al equilibrio quím ico, lO l104
ley ,
de acción de m asas,
para el equilibrio en la fase ga­
seosa, 92;
para soluciones, 117
de A vogadro, 9;
de Boyle, 9;
de D alton, 1, 10;
de las presiones parciales, 10
de D ulong y P etit, 133;
de G ay-Lussac, 9
Sackur-Tetrode, fórm ula de, 139, 140
aplicada al cálculo de la entropía
del vapor de m ercurio, 139;
aplicada al cálculo de la presión
del vapor de un sólido m onoató­
m ico, 138
m áq u in a/s,
caloríficas, 33, 41-42;
refrigerante, 42;
reversibles, 30, 33, 34
térm icas, 41;
y ciclos irreversibles, 34, 36
m em branas,
sem iperm eables a lo s gases, 95, 96;
sem iperm eables a soluciones, 110
m ezcla de gases, 10
m olécula-gram o, 9
m óvil perpetuo de segun da especie,
28
peso e sta d ístico de un estado, 137
Flank, co n sta n te de, 131
postulado de K elvin, 29
potenciales term odinám icos, 72,
a presión con stan te, 77;
a volum en con stan te, 75;
parcial, 99
presión,
atm osférica, 26
crítica, 61
de vapor,
de u n a solución, 121, 123, 125
fórm ula, 63, 64, 138;
osm ótica, 110, 113
de una solu ción n o n n a l, 115
de un electrólito, 115;
en relación con la presión de un
gas ideal, 113
parcial, 9, 10
ley de D alton de la, 10
primera ley de la term odinám ica, 11
aplicada a un ciclo, 16;
en forma diferencial, 18, 19;
form ulación de la, 17, 18
probabilidad,
de un estado term odinàm ico, 53-54,
131;
en relación con la entropía, 53-54,
131;
term odinám ica, 53-54, 130
procesos naturales, dirección de, 5254
prueba cinética de la ley de acción de
m asas, 92
punto,
crítico, 61, 65;
de congelación de una solución, 121128;
de ebullición de una solución, 121,
126, 127;
de inflexión, 61, 65;
triple del agua, 86
r ea cció n /es,
básicas de una solución, 317, IIS;
calor de, 102, 103;
endotérm ica y exotérm ica, 102;
gaseosa, 91
relación de los calores específicos, 2324
Saha, N. M„ 142
segun da ley de la term odinám ica, 28
form ulación de, 29
sem iperm eables, m em branas,
para gases, 94;
para soluciones, 110
sistem as,
de una fase, 85;
de un com ponente, 85;
hom ogéneos, 1, 2;
m ecánicos, 1;
n o hom ogéneos, 2-3;
que con tien en partes m óviles, 3;
qu ím icam ente hom ogéneos, 1;
term odinám icos, 1
sólido qu ím icam en te hom ogéneo, 2
soluciones,
diluidas, 105, 106, 107;
presión del vapor de, 121, 123, 126;
p u nto de ebullición de, 121, 126,
127
sublim ación, 87
tem peratura,
absoluta, 8,
absoluta term odinám ica, 33, 39,
com parada con la tem peratura
de un term óm etro de gas, 39,
50
crítica, 61;
de D ebye, 133;
149
i'I
f;;
fSi ■
»J.
del term òm etro de gas, 8
teorem a de N em st, 129
aplicado a gases, 136, 137;
aplicado a sólidos, 132
teoría cuántica,
en relación con la con stan te de e n ­
tropía, 131, 132;
y los calores específicos, 133
tercera ley de la term odinám ica, 129
term óm etro d e gas, 8
trabajo, 5
efectu ad o por u n gas ideal, 9;
m áxim o que puede efectu ar u n s is ­
tem a, 73-74;
rep resentación geom étrica del, 7
transform aciones, 4,
adiabáticas, 24;
a presión constan te, 8, 77, 78;
a tem peratura c on stan te, 73, 74;
cíclicas, 7;
del e sta ñ o gris en blanco, 134, 135;
isobáricas, 8;
isocoras, 7, 8, 74;
isoentrópicas, 71;
isotérm icas, 8;
reversibles, 4;
unidad de calor, 18
Van der W aals,
ecuación de estado, 65;
ecuación de los esta d o s correspon­
dientes, 69;
esta d o d e un gas de, 70;
isoterm as, 65-66
V an ’t Hoff,
caja de reacción de, 93, 94;
isocora d e, 76
vapor,
m onoatóm ico, 137;
con stan te de entropía, 138, 139;
presión de vapor, 138
satxirado, 59-61
isoterm as de, 59-61
v ariab les de estado, 4
volu m en crítico, 61
mi*
II
ii
s e te m in ó de imprimir en
Talleres Gráficos Carollo,
Av. Díaz Vélez 3461, Buenos Aires,
en el mes de enero de 1985.
lifem

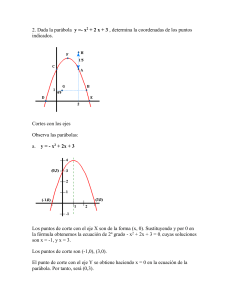





![Prueba Segundos2[1]](http://s2.studylib.es/store/data/003397536_1-3ac4e8618b6474fb10e9bb3037bc9dd2-300x300.png)
