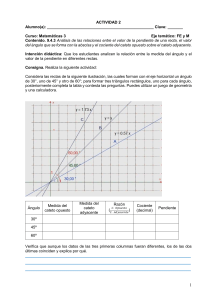
“Año del Fortalecimiento de la Soberanía Nacional” SERVICIO NACIONAL DE ADIESTRAMIENTO EN TRABAJO INDUSTRIAL ESTUDIOS GENERALES INSTRUCTOR: Gamarra Conde Carlos ALUMNO: Edinson Ronaldo Jara Pascual ESPECIALDAD: Electricista Industrial TEMA: Actividad Entregable N°01 Trigonometría Básica SEMESTRE: 2022-10 CFP Huara HUARA – PERÚ 2022-10 ESTUDIOS GENERALES OBJETIVO DEL TRABAJO: Dado el manual, la información técnica y recursos adicionales, los estudiantes serán capaces de elaborar un procedimiento para resolver problemas de trigonometría, presentando un informe por escrito considerando los aspectos de calidad. PLANTEAMIENTO DEL TRABAJO La siguiente gráfica muestra el diseño que corresponde a la instalación de una torre de comunicación alejada de un edificio. La distancia del edifico a la torre es de 24 m y el ángulo de elevación desde ese punto a la parte más alta de la torre es 53º y el ángulo de depresión hacia el pie de la torre es 30º. • ¿Cuál es la altura de la torre? • ¿Cuál es la altura del edificio? • Desarrolle el problema planteado líneas abajo. • Grafique correctamente los símbolos y signos del problema planteado • Utilice los colores apropiados para resaltar y comprender la respuesta del problema. ESTUDIOS GENERALES DESARROLLO DEL TRABAJO F ° 24m 30° e 60 30° 24m ESTUDIOS GENERALES Escribe aquí la ecuación: DATOS: Tan= co/ca Angulo: 53° Cateto opuesto: X Cateto adyacente: 24m Tan53°= 4k/3k 5K Tan53°= 4/3 Tan53°=x/24v 24. tan53°= x 53° 3K 24.4/3 = x 96/3 = x 37° 31,85m = x 4K DATOS: Reemplazamos y operamos: Angulo: 30° Cateto opuesto: y Cateto adyacente: 24m Tan30° = y/24 Tan= co/ca 24. 1/√3 = y Tan30° = k/k√3 24/√ 3 = y Tan30° = 1/√3 Racionalizamos: 24/√3 . √3/√3 = y k√3 30 ° 24/√3/3 = y 2k 8√3 =y 13,86m =y ESTUDIOS GENERALES 60° a) ¿Cuál es la altura de la torre? La altura de la torre (h) es la suma de la altura del edificio (e) y la altura que llamamos f. En el triángulo verde se tiene un ángulo (53°), el lado horizontal o cateto adyacente (24 m) y el lado vertical o cateto opuesto (incógnita f). Sustituimos en la fórmula de la tangente Tg (53°) = f / 24 de aquí 45.71m f = 24 Tg (53°) = 31.85 m Altura de la torre = h = e + f = 13.86 + 31.85 = 45.71 m La altura de la torre es de 45.71 metros. b) ¿Cuál es la altura del edificio? En el triángulo azul se tiene un ángulo (30°), el lado horizontal o cateto adyacente (24 m) y el lado vertical o cateto opuesto (incógnita e). Sustituimos en la fórmula de la tangente Tg (30°) = e / 24 de aquí 13,86m e = 24 Tg (30°) = 13.86 m La altura del edificio es 8√ (3) = 13.86 m. ESTUDIOS GENERALES c) Desarrolle el problema planteado líneas abajo. ¿Porque la torre es más alto que un edificio? - Las torres son construcciones que se caracterizan por su altura. A diferencia de otros edificios que se extienden a lo largo de la superficie, las torres se desarrollan a lo alto. - Las torres se caracteriza en ser de comunicación, electricidad, etc. La altura es algo fundamental entre las torres. - La estructura de tu edificio o 'esqueleto' como se suele denominar, está compuesta por varios elementos. ESTUDIOS GENERALES