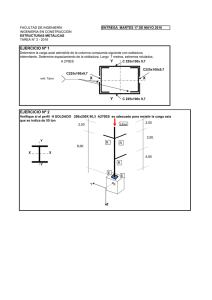
Versión 2014 CAPITULO 4 PROYECTO DE ELEMENTOS DE SUJECIÓN, ANCLAJE Y CIERRE División 1 Cálculo de uniones por pernos Cálculo de uniones por soldadura Cálculo de uniones por pegamento UTN-FRBB Cátedra: Elementos de Máquinas. Profesor: Dr. Ing. Marcelo Tulio Piovan Versión 2014 1. Introducción En esta División del Capítulo 4 se verá la forma de calcular, dimensionar o verificar uniones por pernos y por soldadura, como también uniones por pegamento. Las uniones por soldadura y por pernos revisten características similares en cuanto al tipo de hipótesis empleadas en los modelos de solución. Por otro lado los enfoques analíticos para uniones por pegamento suelen ser particulares del tipo de unión y el esfuerzo predominante en la unión. 2. Uniones por pernos Comparación cualitativa entre las uniones por soldadura y por pernos Los métodos de unión por soldadura y por pernos (o abulonados o atornillados o remachados) suelen tener ciertas diferencias en comportamiento mecánico que los hacen preferibles uno a otro según sea el caso que se trate. En la siguiente Tabla 4.1 se pueden apreciar ventajas y desventajas de las uniones por soldadura y por pernos: Uniones por Soldadura Ventajas Uniones por pernos Ventajas 1) Son herméticas a los fluidos 2) Tienen igual o mayor resistencia que los metales de base 3) Permiten la construcción de piezas muy complejas, imposibles o riesgosas para otros procesos de fabricación a la vez de ser más livianas que sus contrapartes (Fundición) 4) Poseen buena conductividad eléctrica y térmica 5) La resistencia y la rigidez no son afectadas por cambios en la temperatura dentro del margen de servicio de la pieza 1) Se pueden desmontar fácilmente (para inspección o embalaje) 2) Se pueden unir distintos materiales, con distintos tipos de fabricación: compuestos, materiales laminados, tratados térmicamente, etc. 3) Los costos operativos son bajísimos: herramientas de banco y operarios poco calificados. 4) no se presentan tensiones residuales ni alabeos de la estructura. 5) No cambia el tratamiento térmico de las piezas a unir Desventajas Desventajas 1) Puede cambiar el tratamiento térmico de las partes a unir 2) Las juntas no se pueden desmontar. 3) Los elementos se pueden alabear. 4) Se pueden producir tensiones residuales. 5) Pocos metales distintos pueden unirse. 6) Requiere costos operativos elevados: máquinas, operarios calificados y control de calidad 7) Puede que no se detecten poros o microfisuras sin el uso de equipo especial (Rayos X). 1) La junta es débil en las partes que se van a unir 2) acarrea concentraciones tensionales en los agujeros 3) Las uniones no son herméticas a los fluidos 4) pueden tener pobre conductividad eléctrica 5) se pueden aflojar o debilitar ante solicitaciones dinámicas y también ante variaciones de temperatura 6) se puede presentar corrosión en la tuerca o cabeza de perno 7) Suelen requerir planchuelas o suplementos de unión. Tabla 4.1. Ventajas y desventajas de las uniones por soldadura y pernos. Uniones por pernos. Características Generales Existen diferentes tipos de tornillos y de remaches diseñados y construidos para cumplir con roles especiales en distintas aplicaciones y configuraciones de máquinas y de estructuras metálicas mecánicas. En la Figura 4.1 se pueden observar tres tipos clásicos de tornillos, en tanto que en la Figura 4.2 se pueden apreciar algunos ejemplos de remaches. Las formas de la UTN-FRBB Cátedra: Elementos de Máquinas. Profesor: Dr. Ing. Marcelo Tulio Piovan Versión 2014 cabeza y terminación de remaches y tornillos están normalizadas por diversas asociaciones como por ejemplo SAE y DIN entre otras. Figura 4.1. Tipos tornillos. (a) tornillo pasante con tuerca (b) Tornillo de cabeza (c) espárrago Figura 4.2. Tipos de cabezas de remaches. (a) de cabeza roma (b) de cabeza fresada (c) de cabeza cilíndrica En las uniones por pernos suelen distinguirse dos tipos característicos: Uniones por remaches y uniones por tornillos, entre ellos además de gozar de las ventajas y de sufrir las desventajas enumeradas en la Tabla 4.1, poseen entre sí las siguientes ventajas y desventajas: Ventajas de los tornillos sobre los remaches Ventajas de los remaches sobre los tornillos 1) Permiten uniones más fuertes que sus contrapartes 1) No se aflojan por acción de solicitaciones dinámicas remachadas y con posibilidad de graduar el apriete. (vibraciones en general) 2) Permiten con mayor facilidad el desensamblado 2) Son baratos principalmente con relación al proceso de ensamblado. 3) se pueden ensamblar desde los dos extremos Tabla 4.2. Ventajas y desventajas de las uniones por pernos atornillados o remachados Métodos de cálculo de las uniones por pernos Las juntas o uniones por pernos o por remaches suelen tener diferentes patrones y riesgos de falla para una misma condición de solicitación, por ejemplo en la Figura 4.3 se pueden observar tres tipos distintivos de falla en una unión por pernos (remaches o tornillos). Figura 4.3. Tipos de falla característicos en una unión por pernos. UTN-FRBB Cátedra: Elementos de Máquinas. Profesor: Dr. Ing. Marcelo Tulio Piovan Versión 2014 Figura 4.4. Tipos de solicitación en una unión por pernos. Por otro lado en la Figura 4.4 se pueden observar otros tipos de solicitación en las uniones por pernos. Existen diversas condiciones de operación para las piezas o elementos de máquina conectados por medio de remaches o tornillos, algunas formas típicas de solicitación se han introducido a modo de ejemplo en las Figuras 4.3 y 4.4. Sin embargo las uniones por remaches o tornillos suelen ser mayormente solicitadas por una de las siguientes situaciones: I1) I2) I3) I4) I5) I6) I7) Falla por Flexión del perno (tornillo o remache) Falla por Corte Puro de los pernos (tornillo o remache) Falla por tracción de las partes a unir Falla por aplastamiento a compresión del perno Falla por desgarramiento de la parte a unir Falla por efectos combinados: Corte Puro y Corte Torsional Falla por efectos combinados: Corte y Tracción CASO I1): Falla por flexión del perno En la Figura 4.4 se puede apreciar el mecanismo de flexión en el perno. Para evitar la falla, por comportamiento flexional exclusivamente se debe cumplir la siguiente relación: P.L g .c (4.1) 0.6 S yj 2I siendo P la carga separatriz, Lg la longitud de agarre del perno o del tornillo según se aprecia en la Figura 4.5; c e I son respectivamente la distancia a la sección más comprometida y el momento de inercia correspondiente, en tanto que Syj es la tensión límite de fluencia de la parte más comprometida. Téngase presente que Lg = Lt+Ls. UTN-FRBB Cátedra: Elementos de Máquinas. Profesor: Dr. Ing. Marcelo Tulio Piovan Versión 2014 Figura 4.5.Longitud típica de un tornillo. CASO I2): Falla por Corte Puro de los pernos En la Figura 4.6.a se muestra el efecto cortante sobre un perno. Para evitar la falla por corte puro en un perno se debe cumplir la siguiente relación: 4.P S sy 0.4 S y .d c2 (4.2) donde es la tensión de corte, P la carga cortante, dc es el diámetro de la sección resistente, Ssy y Sy son la tensión de fluencia cortante y fluencia de experimento respectivamente (a) (b) Figura 4.6.Mecanismo de corte en un solo perno. La expresión (4.2) es una expresión para la verificación del estado tensional y de la cual puede surgir una expresión para el dimensionado de la junta. Sin embargo cuando se tiene una junta a corte con más de una sección resistente, como en la Figura 4.6.b, el tipo de análisis difiere de la expresión (4.2), debiendo efectuarse un estudio caso-dependiente. En este estudio no se puede hacer otra cosa más que una verificación del estado tensional en los pernos y en las placas o piezas que se unen (ver caso de Estudio N° 7). CASO I3): Falla por tracción de las partes a unir En la Figura 4.7 se muestra el efecto tractivo sobre la unión (que en este caso está compuesta por dos pernos). Para evitar la falla en la línea de pernos se debe cumplir la relación: P S yj hm .bm N R d C (4.3) donde es la tensión de tracción, P la carga, dc es el diámetro de los remaches (o tornillos), Syj es la tensión de fluencia del miembro más débil, hm y bm son el espesor y ancho del miembro más débil y NR el número de remaches en la línea. UTN-FRBB Cátedra: Elementos de Máquinas. Profesor: Dr. Ing. Marcelo Tulio Piovan Versión 2014 Figura 4.7.Mecanismo de falla tractiva en la línea de pernos. CASO I4): Falla por aplastamiento a compresión del perno En la Figura 4.8.a se muestra el efecto aplastamiento por compresión (en el perno o en la junta). Para evitar la falla por aplastamiento se debe cumplir la siguiente relación: P 0.9 S yj d c hm (4.4) donde es la tensión de compresión, P la carga actuante, dc es el diámetro del perno, Syj es la tensión de fluencia del miembro más débil, hm es el espesor (o altura) del miembro más débil. (a) (b) Figura 4.8. (a) Falla por aplastamiento (b) Falla por desgarramiento. CASO I5): Falla por desgarramiento de la parte a unir En la Figura 4.8.b se muestra el efecto cortante de desgarramiento sobre la planchuela. Para evitar esta falla por corte se debe cumplir la siguiente relación: P S sy 0.4 S y 2.hm Ld (4.5) donde es la tensión de corte, P la carga actuante, Ld es la longitud de desgarramiento de la sección resistente y hm es la altura o espesor de la planchuela, Ssy y Sy son la tensión de fluencia cortante y fluencia de experimento respectivamente CASO I6): Falla por efectos combinados: Corte Puro y Corte Torsional En la Figura 4.9 se puede ver un ejemplo genérico de placa plana remachada o atornillada a un bastidor de máquina o estructura. En los pernos de tal placa se generan esfuerzos cortantes de diferente índole. Unos debidos a la acción del corte puro y otro debido a la acción del corte por torsión. Las secciones resistentes de los tornillos pueden ser distintas o bien todas iguales lo cual simplifica mucho los modelos de cálculo. El cálculo de este tipo de uniones es en general de verificación tensional, para secciones resistentes de distinto tamaño y sólo de UTN-FRBB Cátedra: Elementos de Máquinas. Profesor: Dr. Ing. Marcelo Tulio Piovan Versión 2014 dimensionamiento siempre y cuando las secciones resistentes sean todas iguales. El modelo de análisis se basa en dos hipótesis: H1) Las secciones resistentes fallan por corte. H2) La tensión de corte por efecto de torsión es proporcional con la distancia al punto G. Figura 4.9. Pieza remachada solicitada a corte combinado. Figura 4.10. Componente de tensión cortante. Cada una de las secciones resistentes que se observan en la Figura 4.9, ayudan a resistir la fuerza activa F. Esta fuerza se distribuirá de manera diferente en cada una de las secciones. Para entender la metodología es necesario disponer de un centro de reducción de solicitaciones y de ponderación de los esfuerzos, tal centro de reducción G es el centro de gravedad de las áreas resistentes, el cual se puede obtener empleando las siguientes expresiones: NS A x j x j 1 NS A j 1 j NS j A y j , y j 1 NS A j , recordar que el vector r j x j xˆ y y yˆ j j 1 donde Aj es el área de la sección j-ésima. UTN-FRBB Cátedra: Elementos de Máquinas. Profesor: Dr. Ing. Marcelo Tulio Piovan (4.6) Versión 2014 Así pues la sumatoria de todas las fuerzas activas F, se puede reducir en el punto G, obteniendo una fuerza F y un par T r F F (siendo “ ” el operador producto vectorial). La tensión de corte actuante en cada sección, debida a la fuerza F, es denominada “tensión de corte primaria” o “tensión de corte directa” o simplemente “tensión directa” y posee la dirección de la fuerza activa resultante. En cambio la tensión de corte debida a la acción del momento torsor en el punto G es denominada “tensión de corte secundaria” o simplemente “tensión secundaria” o “tensión torsional”. Entonces debido a la presencia de la fuerza y el par, en cada sección resistente habrá dos componentes vectoriales de la tensión de corte, y la tensión cortante total es la suma vectorial de las mismas tal como se puede apreciar en la Figura 4.10. Así pues la tensión directa en la sección j-esima, se puede obtener por medio de la siguiente expresión vectorial: dj F NS A (4.7) j j 1 En cambio la tensión torsional en la sección j-esima, se obtiene con la siguiente expresión vectorial tj T r j NS r j r j A j (4.8) j 1 Siendo “ ” el operador producto escalar o producto vectorial interno. De forma que la tensión cortante total en la sección j-ésima se obtiene sumando las tensiones que resultan de (4.7) y (4.8), es decir: j dj tj (4.9) Luego existirá una falla en la unión si se cumple que: max j S sy 0.4 S y j 1,..., N S (4.10) Las expresiones (4.7) y (4.8) se obtuvieron sobre la base de comparaciones de forma con las homónimas expresiones de la resistencia de materiales para los casos simples de barras rectas (es decir corte puro y torsión). Además, en el caso de que sobre la placa de la Figura 4.9 haya más de una fuerza, en (47) y (4.8) se deberán emplear las correspondientes sumatorias: F NS F j (4.11) j 1 T NS r Fj Fj j 1 UTN-FRBB Cátedra: Elementos de Máquinas. Profesor: Dr. Ing. Marcelo Tulio Piovan (4.12) Versión 2014 CASO I7): Falla por efectos combinados: Corte y Tracción En la Figura 4.11 se puede ver un ejemplo típico de ménsula remachada o atornillada a un bastidor de máquina o estructura. En los pernos de la placa se generan esfuerzos cortantes y esfuerzos tractivos. Los esfuerzos cortantes se deben a la fuerza resistente en el empotramiento, mientras que las fuerzas tractivas se originan por la deformación del zócalo de la ménsula, causada por el momento flector. (a) (b) Figura 4.11. Ménsula empotrada a una columna. Pernos sometidos a corte y tracción El caso que se muestra en la Figura 4.11 es uno de índole elemental para poder fijar ideas. Se supone que los pernos 1 y 2 están sometidos a un estado tensional cortante puro generado por F y cuyo valor es: dj F NS A (4.13) j j 1 Es decir idéntico a (4.7). Sin embargo los mismos pernos también deben soportar esfuerzos tractivos debidos al momento en el empotramiento. Para poder establecer las tensiones tractivas, es necesario establecer las fuerzas de extensión que se ejercen en los pernos. Así pues, se supone que el centro de reducción para el equilibrio de momentos es el punto A, donde actúa la fuerza Fs de contacto entre la pared y el apoyo de la ménsula. Por otro se supone que el apoyo de la ménsula es rígido y rota respecto de A un ángulo infinitesimal , en consecuencia se puede establecer una relación de compatibilidad entre las deformaciones de los pernos. También se supone que la línea de centros de pernos y la línea de acción de la carga se encuentran en el mismo plano. Así pues por equilibrio de momentos se tiene: F.LF F1 L 1 F2 L 2 (4.14) Las fuerzas tractivas en cada perno se pueden escribir como: F1 1 A1 1 E.A1 y F2 2 A1 2 E.A2 (4.15) Luego las deformaciones específicas se pueden obtener en función de condiciones de compatibilidad (aduciendo la hipótesis de que el apoyo de la ménsula es rígido), de manera que: UTN-FRBB Cátedra: Elementos de Máquinas. Profesor: Dr. Ing. Marcelo Tulio Piovan Versión 2014 1 L P 1 LP 1 .L1 LP 1 2 , L P 2 LP 2 .L2 LP 2 (4.16) siendo LP1 y LP2 las longitudes de los pernos (que se tomarán genéricas, aunque en el caso de la Figura 4.11 son iguales). En virtud que en (4.16), es el mismo, se puede establecer una relación con la cual despejar una de las dos deformaciones en función de la restante, es decir: 2 1 LP1 L2 LP 2 L1 (4.17) Así pues, (4.17) y reemplazando en (4.15) y luego en (4.14) se pueden obtener la deformación 1 como: 1 F.L F A L2 L E A1 L1 2 2 P1 L1 LP 2 (4.18) Luego reemplazando (4.18) en (4.17) se obtiene e2. Con e1 y e2 se obtienen las tensiones tractivas, es decir: j E. j con j 1,...,2 (4.19) Obviamente con (4.19) se puede obtener el valor de las fuerzas. Con (4.19) y (4.13) se tienen que calcular las tensiones principales (ver expresiones (2.27) a (2.34) en el Capítulo 2 División 2 o bien en el Apéndice 3) para luego emplear alguna de las teorías de rotura estática como las vistas en el Capítulo 2 División 4. Si se trata de una carga dinámica y el análisis por fatiga se emplearán los métodos del Capítulo 2 División 5. 3. Métodos de cálculo de las uniones por soldadura Las uniones por soldadura poseen diversas características por si mismas según el método empleado. Sin embargo todos los métodos tienen en común que las partes a unir se funden localmente para formar un conjunto. Uno de los métodos más convencionalmente empleado es la soldadura por arco o soldadura eléctrica, dentro de la cual hay una variada gama que depende de las condiciones de operación y de protección de la fusión de los materiales a unir. Así por ejemplo en la Figura 4.12 se pueden ver diferentes casos geométricos de soldaduras. Estas son denominadas soldaduras a tope o soldadura en filete, las cuales pueden hallarse sometidas a esfuerzos netamente tractivos o a esfuerzos cortantes. En la Figura 4.12.a el esfuerzo predominante es tractivo, en las Figuras 4.12.b y 4.12.c el esfuerzo predominante es de corte, mientras que en la Figura 4.12.d existe una composición de esfuerzos cortantes y de esfuerzos tractivos. Para analizar la resistencia de la unión soldada se suele emplear la hipótesis de que la sección resistente es la que se muestra en la Figura 4.13.a, la cual es denominada “garganta de la UTN-FRBB Cátedra: Elementos de Máquinas. Profesor: Dr. Ing. Marcelo Tulio Piovan Versión 2014 soldadura”. Así pues, en los casos (a) Y (b) de la Figura 4.12, la formula de resistencia es claramente elemental. En el caso de la Figura 4.12.c la formula de resistencia es la siguiente τ P 2P P 1.414 hg .L h.L 2 .h.L Tipo: Junta o soldadura a tope Esfuerzo de tracción (4.20) Tipo: Junta o soldadura a Tope Esfuerzo de corte (b) (a) Tipo: Soldadura de filete Tipo: Soldadura de filete Esfuerzo normal a la longitud del filete Esfuerzo de corte (c) (d) Figura 4.12. Diferentes tipos de soldaduras (a) (b) Figura 4.13. Garganta de una soldadura a filete Ahora bien en el caso de la Figura 4.12.d, la fórmula de la tensión de corte se puede obtener siguiendo el diagrama de cuerpo libre de la Figura 4.14, como: τ 2P P 1.414 h.L 2.h.L (4.21) Se puede ver, entonces, que los dos cordones de soldadura de la Figura 4.13.b se pueden calcular al corte empleando la misma expresión (4.20) o (4.21). UTN-FRBB Cátedra: Elementos de Máquinas. Profesor: Dr. Ing. Marcelo Tulio Piovan Versión 2014 De la misma manera se puede obtener de la Figura 4.14, ya que Sen[45]=Cos[45]. Figura 4.14. Diagrama de cuerpo libre de una junta de filete Las uniones por soldadura se pueden calcular a una o más de las siguientes condiciones de trabajo: II1) II2) Falla por efectos combinados: Corte Puro y Corte Torsional Falla por efectos combinados: Corte y Tracción y/o compresión Los casos II1) y II2) de uniones por soldadura son similares a los casos I6) y I7) de uniones por remaches o tornillos, con la diferencia que ahora las secciones resistentes son continuas y conformadas por la sumatoria de las “secciones de garganta”. CASO II1): Falla por efectos combinados: Corte Puro y Corte Torsional En la Figura 4.15 se muestra la placa de las Figuras 4.9 y 4.10 pero ahora unida al bastidor por medio de cordones de soldadura. Donde ahora el punto G es el centroide de la línea de cordones de soldadura. Esta placa tiene cordones de soldadura dispuestos en forma genérica cuyos esfuerzos resistentes difícilmente sean equiparables a los esfuerzos de tracción y corte elementales presentados en las Figuras 4.12 a 4.14. Figura 4.15. Placa soldada a un bastidor UTN-FRBB Cátedra: Elementos de Máquinas. Profesor: Dr. Ing. Marcelo Tulio Piovan Versión 2014 Sin embargo en virtud de la similitud de las expresiones (4.20) y (4.21) para la ponderación del estado de tensión cortante en dos condiciones de solicitación diferente, se puede mantener en forma aproximada las mismas hipótesis empleadas para calcular el estado tensional en la homónima unión por pernos, es decir el caso I6). En consecuencia las hipótesis para el cálculo de esta condición de carga son: H1) Las secciones resistentes fallan por corte. H2) La tensión de corte por efecto de torsión es proporcional con la distancia al punto G. En consecuencia, a comparación del Caso I6), se deben sumar vectorialmente las componentes de la tensión de corte debidas al corte directo y al corte por efecto torsional. Esta operatoria se hace en los puntos más críticos del cordón de soldaduras. Estos, según se pueden apreciar en la Figura 4.15, con los números 1 a 6, se ubican en los extremos de los cordones de soldadura, siempre y cuando el cordón de soldadura tenga la misma calidad en todo el tramo, de lo contrario la técnica de cálculo que aquí se ofrece no tiene sentido. Entonces las tensiones directa y secundaria se obtienen según (4.22) y (4.23) respectivamente y la tensión total en el punto j-ésimo según (4.24). dj F NS Ai i 1 tj T r j NS i 1 Li 1 Li r 2 hg dL F F NS hgi Li i 1 2 2 T r j 2 2 NS i 1 Li 1 Li r 2 hdL NS (4.22) hi Li i 1 T r j JS , con j = 1,... NP j dj tj (4.23) (4.24) En las expresiones anteriores NS y NP son el número de cordones y el número de puntos de cálculo, respectivamente. Li y Li+1 son los límites de integración en la dirección tangencial del cordón de soldadura, para cada tramo. JS es el momento de inercia polar de todos los cordones de soldadura con respecto al punto G. Luego existirá una falla en la unión si se cumple que: max j S sy j 1,..., N P (4.25) Siendo Ssy la tensión de fluencia al corte del material de aporte para hacer el cordón de soldadura. Si bien las expresiones (4.22) a (4.25) son generales, la parte más compleja de la rutina de análisis reside en el cálculo de JS. Para aliviar tal operatoria, muchas veces se cuenta con JS para los casos más comunes calculados y tabulados para la misma altura de garganta hg. Tales valores se pueden hallar en la Tabla 4.3. Para seguir algunos aspectos de cálculo véase el Caso de Estudio No 7. UTN-FRBB Cátedra: Elementos de Máquinas. Profesor: Dr. Ing. Marcelo Tulio Piovan Versión 2014 Dimensiones y tipo de soldadura Esquema o gráfico Caso de corte con torsión A, G JS A hg d JS A 2 hg d JS A 2 hg b JS A hg d b x , y b ,d 2 2 2d b A hg d 2b x 2 b d 2b A hg d 2d y 2 d 2d b JS hg d 3 12 hg d 3 3db 2 6 hg 3bd 2 b 3 6 hg b d 6d 2b 2 4 12b d 8b3 6 bd 2 d 3 b4 J S hg 12 2b d 8 d 3 6 db 2 b3 d4 J S hg 12 2d b A 2hg d b A hg d hg d b 3 JS JS 6 hg d 3 4 Tabla 4.3. Formas de soldaduras básicas y sus constantes de cálculo. (Recordar que hg = 0.707 h) UTN-FRBB Cátedra: Elementos de Máquinas. Profesor: Dr. Ing. Marcelo Tulio Piovan Versión 2014 A los efectos de calcular JS, recuérdese que también se puede emplear la regla de suma de momentos de segundo orden de áreas y el Teorema de Steiner es decir: JS NS i 1 Li 1 Li r hg dL 2 J A r , con i = 1,... N NS i 2 i ci S (4.26) i 1 donde Ji es el momento de inercia polar del cordón i-esimo respecto de su centroide, Ai es el área de la sección de la garganta y rci es la distancia del centro G al centro del cordón i-esimo. CASO II2): Falla por efectos combinados: Corte y Tracción y/o compresión En la Figura 4.16 se puede apreciar una pieza soldada a un bastidor y sometida a esfuerzos combinados debido a la acción de flexión. La forma de cálculo por verificación para este tipo de soldaduras siguen un patrón similar al del caso I7) para uniones por pernos. Para desarrollar el modelo de cálculo es necesario considerar las siguientes hipótesis: H1) Tensión de corte debida a fuerza cortante (Tensión primaria) H2) Tensión normal debida a momento flector (Tensión secundaria) H3) Se supone que la tensión secundaria en un punto de la garganta, es normal a la misma. Lo cual es una suposición fuerte y aproximadamente válida para algunos casos. H4) Se supone que la tensión primaria es uniforme en todo el grupo de soldaduras H5) La línea neutra flexional pasa por el centroide del grupo de soldaduras (Punto G) H6) Las áreas involucradas corresponden a las de cada garganta de filete del grupo de soldaduras Figura 4.16. Pieza soldada a un bastidor sometida corte y tracción (o compresión) debidas a flexión UTN-FRBB Cátedra: Elementos de Máquinas. Profesor: Dr. Ing. Marcelo Tulio Piovan Versión 2014 En primer lugar se debe ubicar el centroide del conjunto de cordones de soldadura (punto G). Luego se deben hallar las tensiones primaria y secundaria en los puntos conflictivos, según las expresiones (4.27) y (4.28) respectivamente: dj F F NS A h i i 1 sj r ˆj h dL M r ˆj NS i 1 Li 1 Li 2 g gi F NS Li i 1 2 2 NS h L i (4.27) i i 1 Mc I 2 r ˆj hdL 2 M r ˆj NS i 1 Li 1 2 j , con j = 1,... NP U (4.28) Li En las expresiones anteriores jˆ es el vector unitario en la dirección donde actúa la carga F, cj es la distancia a la Fibra más solicitada en el punto j-ésimo. IU es el momento de inercia del conjunto de cordones de soldaduras. En la Tabla 4.4 se presentan algunos valores de IU para condiciones de solicitación y geometrías convencionales. Luego de determinar la tensión cortante y la tensión normal se obtienen las tensiones principales según la (4.29) y finalmente se emplea alguno de los criterios de falla estática o dinámica vistos en el Capítulo 2 (divisiones 4 y 5 para estática y dinámica-fatiga, respectivamente). sj 1 j , 2 j sj dj 2 2 2 2 (4.29) Notas sobre las formas de los filetes de soldadura En la Figura 4.17 se muestran casos de terminación óptima de los perfiles de filete para los cuales son válidos los modelos de cálculo presentados en los apartados anteriores. Se debe tener presente que las técnicas de cálculo simplificadas son muy sensibles a los cambios en el acabado y calidad de la junta de soldadura como también del tipo de electrodo que se emplea (Figura 4.17.c). Mayores precisiones sobre este particular se pueden hallar en la referencia [5]. En la Página web de la AWS se pueden hallar otros detalles de provecho para las uniones soldadas. UTN-FRBB Cátedra: Elementos de Máquinas. Profesor: Dr. Ing. Marcelo Tulio Piovan Versión 2014 Figura 4.17. Características de terminación y penetración de los perfiles de filete. Dimensiones y tipo de soldadura Esquema o gráfico Caso de corte con flexión A, G IU A hg d IU A 2 hg d IU A 2 hg b IU A hg d b x , y b , d 2 2 2d b IU x b d 2b IU hg UTN-FRBB Cátedra: Elementos de Máquinas. Profesor: Dr. Ing. Marcelo Tulio Piovan 12 hg d 3 6 hg d 2b 2 hg d 3 4b d A hg d 2b 2 hg d 3 12b d d2 6b d 12 Versión 2014 A hg b 2d y IU 2 d 2d b A 2hg d b hg d 3 2b d 3b 2d IU hg A hg d IU d2 3b d 6 hg d 3 8 Tabla 4.4. Formas de soldaduras básicas y sus constantes de cálculo. (Recordar que hg = 0.707 h) Resistencia de la Soldadura En la Tabla 4.5 se indican algunos valores de resistencia mínima del alambre de los electrodos clásicos. Por otro lado, en la Tabla 4.6 se indican algunos valores de los coeficientes de concentración de tensiones que suelen utilizarse para el cálculo por fatiga (KF). Número de electrodo Resistencia a rotura Resistencia a la Alargamiento (AWS) tractiva [ksi] fluencia [ksi] porcentual E60XX 62 50 17-25 E70XX 70 57 22 E80XX 80 67 19 E90XX 90 77 14-17 E100XX 100 87 13-16 E120XX 120 107 14 Tabla 4.5. Resistencia de electrodos según AWS Tipo de soldadura KF Soldadura a tope reforzada 1.2 Borde de soldadura a filete transversal 1.5 Extremo de soldadura a filete paralela 2.7 Junta a tope en T con esquinas agudas 2.0 Tabla 4.6. Coeficientes de concentración de tensiones para fatiga UTN-FRBB Cátedra: Elementos de Máquinas. Profesor: Dr. Ing. Marcelo Tulio Piovan Versión 2014 4. Uniones por pegamento La unión por pegamento, es el proceso de unir materiales químicamente por la interacción intermolecular o interatómica. Este tipo de unión es muy útil para unir materiales de diversa índole. En la Tabla 4.7 se muestran algunas de las ventajas y desventajas de las uniones por pegamento frente a las uniones por soldadura y por pernos. Ventajas Desventajas 1) se permite una gran reducción de peso estructural 2) Posee resistencia a la fatiga adicional por su flexibilidad 3) Se pueden unir materiales gruesos o delgados 4) La distribuye de manera más uniforme (aumento de vida) 5) Las juntas son a prueba de fugas 6) Puede amortiguar vibraciones 7) Tiene la habilidad de unir materiales disímiles 1) Se debe preparar adecuadamente la superficie 2) Existe limitación en la temperatura de servicio (T<260°C) 3) No es muy durable a largo plazo. 4) Deterioro de la unión por deformaciones progresivas a lo largo del tiempo (efecto creep, material viscoelástico) Tabla 4.7. Ventajas y desventajas de las uniones por pegamento. En la Figura 4.18 se muestran distintas formas de efectuar la unión por pegamento entre placas. Las formas más populares y efectivas son las denominadas junta de solapa (simple o doble) y junta oblicua. Los modelos de análisis y cálculo de juntas por pegamento suelen ser materia de constante modificación y validación con respecto a resultados experimentales y casi siempre los modelos disponibles están asociados a un tipo de pegamento en particular. Sin embargo existe un enfoque suficientemente general para el estudio de tensiones en una junta de solapa simple aunque limitado a una hipótesis de comportamiento elástico en el pegamento. Figura 4.18. Formas de juntas para unión por pegamento El modelo matemático para la junta de solapa simple (ver Figura 4.18) se basa en suponer lo siguiente: H1) las placas tienen movimiento horizontal exclusivamente H2) no se considera flexión en las placas y la deformación de las placas se debe solo a la acción de las cargas actuantes en sus extremos. H3) Se supone que la fuerza de contacto entre el adhesivo y la placa varía según F x F .x n UTN-FRBB Cátedra: Elementos de Máquinas. Profesor: Dr. Ing. Marcelo Tulio Piovan Versión 2014 H4) Las placas a unir tienen el mismo ancho, aunque pueden ser de distinto material. Así pues el desplazamiento axial de la placa en la parte en contacto tiene la siguiente forma: xx du xx F ( x) F u x x n 1 dx E EA EAn 1 (4.30) Se desprende que si n =1 el desplazamiento tendrá forma cuadrática a partir del extremo conectado de la placa, tal como se ve en la Figura 4.19. El modelo matemático que describe el estado tensional del pegamento para una junta por solapa simple es (ver desarrollo y deducción en [4]): 1 d 2 Ea 1 2 K a 0 con K a 2 2 dx 2ha 1 a E1 h1 E2 h2 (4.31) donde Ea, a y ha son el módulo de elasticidad del pegamento, coeficiente de Poisson del pegamento y espesor del pegamento, mientras que Ei y hi son módulo de elasticidad y espesor de las placas. Es claro que la expresión (4.31) contempla la adhesión de dos materiales diferentes. La solución de la ecuación (4.31) con las debidas condiciones de borde permite establecer el valor del estado tensional en el pegamento y la distribución de fuerzas de adhesión. En la Tabla 4.8 se dan algunos valores indicativos para las resistencias al retraso de ciertos pegamentos. Figura 4.19. Distribución de la deformación. Módulo de Resistencia al elasticidad Ea desprendimiento [Gpa] [kN/m] Celulósicos 0.35 a 3.50 0.70 0.18 a 1.80 Uretano 6.9 a 17.2 1.50 1.8 a 8.8 fenólico modificado 13.8 a 27.6 3.80 3.6 a 7.0 Epoxico sin modificar 10.3 a 27.6 3.50 0.35 a 1.80 Poliimida 13.8 a 27.6 3.80 0.18 a 0.88 Tabla 4.8. Valores típicos de resistencia y elasticidad de algunos adhesivos. Tipo o química del adhesivo Resistencia al retraso de corte [Mpa] 5. Bibliografía [1] J.E. Shigley y C.R. Mischke, “Diseño en Ingeniería Mecánica”, McGraw Hill 2002. [2] B.J. Hamrock, B. Jacobson y S.R. Schmid, “Elementos de Máquinas”, McGraw Hill 2000. [3] R.L. Norton, “Diseño de maquinaria”, McGraw Hill 2000. UTN-FRBB Cátedra: Elementos de Máquinas. Profesor: Dr. Ing. Marcelo Tulio Piovan Versión 2014 [4] W.C. Orthwein, “Diseño de componentes de máquinas” Ed CECSA, 1996. [5] E. Asta, “Soldadura de filete, diseño y práctica” Soldar Conarco N° 121, 5-9 (2004) [6] American Welding Society. http://www.aws.org. [7] K. Lingaiah, “Machine Design Databook”, Digital Engineering Library, McGraw-Hill 2004. http://www.digitalengineeringlibrary.com. 6. Problemas resueltos y para completar Problema resuelto 1. En las Figuras a y b se puede ver la distribución de pernos y de cordones de soldadura para resistir a una carga de 1000 libras. Las dimensiones están en pulgadas. (a) (b) Condiciones de la unión por tornillos: - Los tornillos A y C son de 5/8 pulg y los tornillos B y D son de 7/8 pulg. - La tensión de fluencia de los tornillos es de 85000 psi. Condiciones de la Unión por soldadura: - Todos los cordones tienen aproximadamente una altura de cateto de 3/16 pulg. - El alambre del electrodo tiene una resistencia a la fluencia de 67000 psi. En ambos casos se desea obtener el coeficiente de seguridad de las uniones Solución del problema Caso de tornillos En primer lugar se debe determinar el área resistente de los tornillos: A 2 2 5 7 A j 1.816 pul 2 , 2 8 8 j 1 NS Luego se deben determinar las coordenadas del centro de las secciones resistentes: NS A x j x j 1 NS A NS j A y j 4.635 pul , y j j 1 j 1 NS A j 3.000 pul j j 1 Luego la excentricidad de la carga será: UTN-FRBB Cátedra: Elementos de Máquinas. Profesor: Dr. Ing. Marcelo Tulio Piovan Versión 2014 eC 7 8 x (15 4.635) pul 10.360 pul Debido a la simetría con respecto al eje x, las distancias entre el centroide a las secciones A y C es la misma, y la distancia del centroide a las secciones B y D es la misma y vienen dadas por: rA rC 5.521 pul rB rD 3.820 pul La tensión directa por corte puro será: dj F NS A 1000lib 550.7 psi 1.816 pul 2 j j 1 La tensión secundaria será la misma para las secciones A y C, y tendrá otro valor para las secciones D y B. Estas vienen dadas por la siguiente expresión vectorial tj T r j NS r j r j A j j 1 Los valores absolutos de las tensiones son: tA tC 1577 psi tB tD 1091 psi Luego la composición vectorial de las tensiones directas y secundarias dará: A C 1154 psi B D 1496 psi Nótese que los pernos más grandes son los que resisten la mayor tensión, en consecuencia el coeficiente de seguridad se obtiene de la expresión max j S sy 0.4 S y j 1,..., N S Es decir nS 0.4 S y 0.4 85000 22.727 B 1496 Caso de cordones de soldadura En primer lugar se debe calcular la altura de garganta como: 2 23 h 0.133 pul 2 2 16 Luego la ubicación del centroide de secciones, del área resistente y del momento de inercia polar de la unión soldada se obtienen de la Tabla 4.3, que se adjunta a continuación: hg UTN-FRBB Cátedra: Elementos de Máquinas. Profesor: Dr. Ing. Marcelo Tulio Piovan Versión 2014 A hg d 2b x 2 b 2b d 2b d 3 b d 2 b 2 J S hg 2b d 12 en consecuencia x 2.042 pul A 3.192 pul 2 J S 74.74 pul 4 Luego la excentricidad será: eC (7 8 x ) 12.958 pul La tensión directa viene dada por la siguiente expresión dj F NS A 1000lib 255.62 psi 3.192 pul 2 j j 1 La tensión secundaria viene dada por: tj T r j NS i 1 Li 1 Li r hg dL T r j 2 2 2 NS i 1 Li 1 Li r hdL T r j 2 JS , con j = 1,... NP Nuevamente por la simetría respecto del eje horizontal las tensiones en los puntos A y C son las mismas y las tensiones en los puntos B y D son iguales. Los valores absolutos de las tensiones secundarias son: tA tC 936.22 psi tB tD 1220.73 psi Luego la composición vectorial de las tensiones directas y secundarias dará: A C 872.25 psi B D 1412.45 psi El coeficiente de seguridad se obtiene de la expresión max j S sy j 1,..., N P Es decir nS 0.4 S y 0.4 67000 18.974 B 1412.45 Conclusiones ¿Que conclusiones se pueden extraer de estos dos casos?. ¿Cual opción convendría utilizar destacando los costos operativos?. ¿Cual convendrá utilizar en función de resistencia? UTN-FRBB Cátedra: Elementos de Máquinas. Profesor: Dr. Ing. Marcelo Tulio Piovan Versión 2014 7. Problemas propuestos Problema 1. Hallar la carga cortante total en cada uno de los pernos que unen la planchuela a la columna en el esquema de la Figura adjunta. Calcular también las tensiones de corte en todos los pernos y la tensión de aplastamiento en los pernos que corresponda. Tendrá sentido calcular la tensión normal en la placa en un punto como el B. Problema 1 Problema 2 Problema 2. Una placa de acero como la que se presenta en la Figura adjunta está soldada a una columna metálica. Las dimensiones están dadas en el sistema inglés (pulgadas). La carga vertical W = 4000 lbf actúa a 6.8 pulg desde la soldadura de la izquierda. Ambas soldaduras fueron practicadas según AWS (American Welding Society) empleando el electrodo tipo E8000. La tensión de corte permitida en la soldadura se debe calcular empleando un factor de seguridad ns = 3.0 y con un valor de resistencia por corte a la fluencia de SSy = 0.25 SU (compare luego con la SSy = 0.40 SY). Calcular a su vez la longitud de garganta de la soldadura y la longitud del cateto de la soldadura. Problema 3. Una placa para armar una ménsula que soporta un motor eléctrico, se conecta con tornillos a una viga de acero como se muestra en la Figura adjunta. Suponer acero de bajo carbono y que la resistencia a la fluencia de los tornillos es de 600 Mpa. Se aplica una carga de 24 kN y suponiendo un factor de seguridad de 3, calcular el diámetro de los tornillos y según un catálogo comercial elegir el más apropiado en mercado. Problema 4. Una Barra de acero como la de la Figura adjunta, está soldada por un electrodo E60XX a la pared. Se aplica una carga de 3500 N en el extremo de la barra y en la dirección indicada. UTN-FRBB Cátedra: Elementos de Máquinas. Profesor: Dr. Ing. Marcelo Tulio Piovan Versión 2014 Calcular el factor de seguridad de las soldaduras contra la fluencia. Cambiará el factor de seguridad si la misma carga se aplica en la dirección z. Dimensiones en mm. Problema 5. Se desea montar la ménsula para que soporte una carga colgante de 500 kg según como se ve el sistema de la figura. Se piensa utilizar el electrodo E80XX en cuatro cordones de soldadura iguales según el boceto. Si los cordones de soldadura pueden tener 4 mm o 6 mm de cateto, determine si, con la longitud de los cordones de soldadura existentes, se garantiza la resistencia del montaje. El límite de fluencia al corte es el 57% del límite de fluencia dado por tabla. Las medidas están en mm. Problema 6. Se desea montar la ménsula para soportar un motor de 300 kg según se ve en la figura. Se desea emplear electrodos E60XX o E80XX según como resulten los sondeos previos de resistencia. Determine el tamaño de filete de soldadura que, para un coeficiente de seguridad 2, pueda resistir el peso estáticamente. El límite de fluencia al corte es del 45% del límite de fluencia dado por tabla. Las medidas están en mm. Problema 5 Problema 6 Problema 7. De acuerdo con los datos del Problema 5, se desea calcular la vida a fatiga si desde el valor de la carga hay una fluctuación de ±100 kg cada 30 seg. Para calcular las tensiones reales bajo fatiga se debe afectar las tensiones nominales por un coeficiente KF = 2. Emplee la información del mencionado problema. Problema 8. Una placa de acero se fijará, por medio de pernos roblonados, a un montante metálico como se muestra en la figura. Si el límite de fluencia de la placa es 40000 psi y el límite de fluencia de los pernos es de 50000 psi, con límite de fluencia al corte de 57% del de fluencia. Determine los coeficientes de seguridad para todas las posibles situaciones de falla en cada parte de la unión. Los pernos tienen un diámetro de ¾ pulgada. UTN-FRBB Cátedra: Elementos de Máquinas. Profesor: Dr. Ing. Marcelo Tulio Piovan Versión 2014 Problema 8 Problema 9 Problema 9. Se desea resolver el problema 6 teniendo en cuenta ahora una unión por bulones. Se emplearán 3 bulones por lado. Se desea establecer para la carga dada el diámetro de los bulones (todos iguales) con un factor de seguridad que no sea menor que 4 y el grado de los mismos (ver Apéndice 6, Tabla A6.2) tal que sea la construcción más económica suponiendo que a mayor grado mayor costo. Problema 10. Cálculo de uniones por pernos Determinar los coeficientes de seguridad de cada uno de los pernos que forman el anclaje de la ménsula que se muestra en la Figura. Los pernos tienen diámetro de ¾ pulgada. El límite de fluencia del material de los pernos es de 600 MPa. Las dimensiones están en mm. La carga es de 5000 N. UTN-FRBB Cátedra: Elementos de Máquinas. Profesor: Dr. Ing. Marcelo Tulio Piovan