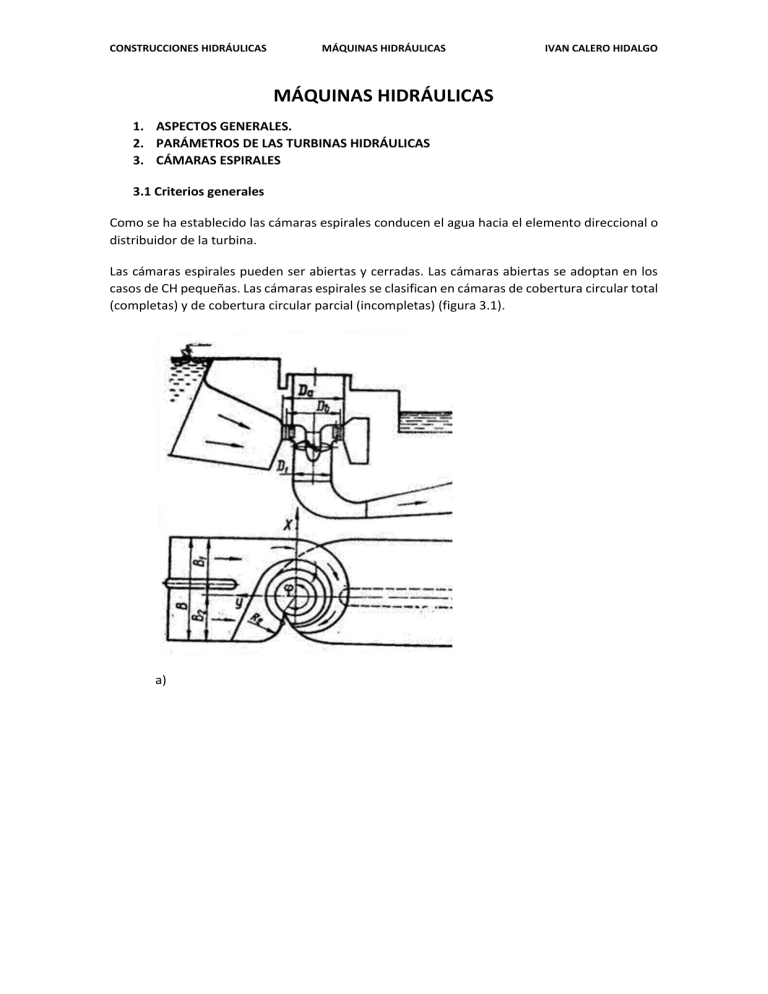
CONSTRUCCIONES HIDRÁULICAS MÁQUINAS HIDRÁULICAS IVAN CALERO HIDALGO MÁQUINAS HIDRÁULICAS 1. ASPECTOS GENERALES. 2. PARÁMETROS DE LAS TURBINAS HIDRÁULICAS 3. CÁMARAS ESPIRALES 3.1 Criterios generales Como se ha establecido las cámaras espirales conducen el agua hacia el elemento direccional o distribuidor de la turbina. Las cámaras espirales pueden ser abiertas y cerradas. Las cámaras abiertas se adoptan en los casos de CH pequeñas. Las cámaras espirales se clasifican en cámaras de cobertura circular total (completas) y de cobertura circular parcial (incompletas) (figura 3.1). a) CONSTRUCCIONES HIDRÁULICAS MÁQUINAS HIDRÁULICAS IVAN CALERO HIDALGO b) Figura 3.1 a) cámara espiral de hormigón con ángulo de cobertura parcial; b) cámara espiral metálica con ángulo de cobertura total. En las cámaras espirales de cobertura circular total el ángulo de cobertura 𝜑 es de casi 360 grados, generalmente 𝜑𝑚𝑎𝑥 = 345 𝑔𝑟𝑎𝑑𝑜𝑠. En las cámaras espirales de cobertura circular parcial el ángulo de cobertura 𝜑=165÷225 grados. El ángulo de la espiral 𝜑 se mide desde la punta de la espiral, en dirección contraria a la del movimiento del agua, hasta la sección de entrada. El agua conducida a la turbina se distribuye mejor en los casos de espirales con cobertura total, sin embargo, estas cámaras espírales requieren de mayor espacio en planta y por tanto exigen de mayores volúmenes de obra. Generalmente las cámaras espirales de cobertura total se adoptan en casos de cargas grandes, cuando el agua a la CH es entregada por tuberías. Las cámaras espirales de cobertura parcial se utilizan en casos de cargas pequeñas y caudales de agua grandes, cuando el agua se entrega a la cámara desde la entrada abierta de la CH. Las cámaras espirales de cobertura parcial son generalmente de sección en T de hormigón armado, se adoptan para cargas de hasta 30÷40 metros. Las cámaras espirales de cobertura total son metálicas y de sección circular. 3.2 Análisis grafo-analítico de una cámara espiral. 3.2.1 El tipo de cámara espiral se adopta a partir de los gráficos relativos a los campos de aplicación de las turbinas y a las características universales, en las cuales se incluye el tipo recomendado de cámara espiral: VA- turbina vertical, cámara abierta; VHturbina vertical, cámara de hormigón armado; VM- turbina vertical, cámara metálica; HA- turbina horizontal, cámara abierta. 3.2.2 En el caso cuando para el tipo seleccionado de turbina son posibles dos tipos de cámaras espirales (por ejemplo, VH y VM), se realiza el análisis técnico económico para seleccionar la variante óptima. CONSTRUCCIONES HIDRÁULICAS MÁQUINAS HIDRÁULICAS IVAN CALERO HIDALGO La selección del tipo óptimo de cámara espiral se ejecuta a partir de la condición de obtener el ancho mínimo del bloque (hidro-agregado), que debe ser implantando en el macizo sumergido con los elementos de conducción de la turbina (cámara espiral y conducto de restitución o tubo de aspiración) y de las estructuras de desagüe incorporadas, para lo cual es necesario formular la implantación esquemática de la construcción bajo agua del bloque hidro-energético, con los tipos considerados de la cámara espiral, conducto de restitución y estructuras de desagüe. 3.2.3 El ángulo de cobertura de las cámaras de hormigón armado, en la mayoría de los casos se adopta de 180 grados, en tanto que para las cámaras metálicas de 345 grados. 3.2.4 Es posible la inobservancia de estas recomendaciones, debido a las condiciones de implantación del bloque, particularmente en lo que respecta a los desagües incorporados. 3.2.5 El análisis hidráulico de las cámaras espirales de hormigón y metálicas puede ejecutarse por uno de los dos métodos básicos: a) Por la ley de constancia de las velocidades medias, 𝑣𝑚𝑒𝑑 = 𝑐𝑜𝑛𝑠𝑡.; b) Por el método de constancia del momento de la velocidad: 𝑣𝑢 𝑟 = 𝑐𝑜𝑛𝑠𝑡. El análisis hidráulico de las cámaras espirales de hormigón con ángulo de cobertura 𝜑 = 180° puede ser realizado por cualquiera de los dos métodos, por cuanto las dimensiones en planta de la cámara y sus indicadores energéticos se obtienen prácticamente iguales. Para las cámaras espirales metálicas, con ángulo de cobertura 𝜑 = 345° el análisis hidráulico por la ley de constancia del momento de la velocidad permite obtener menores dimensiones en planta de la cámara espiral. Sin embargo, al aplicar el método de la constancia de la velocidad media se obtienen mejores condiciones hidráulicas. 3.2.6 El análisis hidráulico de las cámaras espirales se inicia con la determinación de sección de entrada. El área y los parámetros en la sección de entrada de la cámara espiral se determina con las ecuaciones: Área de la sección de entrada 𝐹= 𝑄 𝑉𝑒𝑛𝑡 Caudal de diseño de la cámara espiral 𝑄𝐷𝐼𝑆 = 𝑄𝜑𝑜 360𝑜 Velocidad media en la entrada a la cámara espiral: 𝑉𝑒𝑛𝑡 = 𝐾𝑉 √𝐻 Dónde, 𝜑𝑜 - ángulo de cobertura de la cámara espiral; 𝐾𝑉 - coeficiente de velocidad. CONSTRUCCIONES HIDRÁULICAS MÁQUINAS HIDRÁULICAS IVAN CALERO HIDALGO Pará cálculo preliminar se puede asumir: para las turbinas Kaplan, en caso de cámara de hormigón, 𝐾𝑉 = 0,7 ÷ 0,8; en caso de cámara espiral metálica, 𝐾𝑉 = 0,8 ÷ 0,9. El área de la sección de entrada puede ser determinada con la ecuación: 𝐹= 𝑚𝑄𝐼′ 𝐷12 𝐾𝑉 Dónde, 𝑄𝐼′ - caudal relativo de la turbina que se determina con la ecuación: 𝑄𝐼′ = 𝑄 𝐷12 √𝐻 Dónde, 𝐷1- diámetro del rodete, m. 𝑚- coeficiente que expresa la relación del ángulo de cobertura de la espiral al ángulo del circulo completo, es decir: 𝑚= 𝜑𝑜 360 𝐻- carga de diseño, m. 3.2.7 Las dimensiones de la sección de entrada se determinan con las ecuaciones de la geometría básica. Para el caso de la cámara espiral metálica: 𝐹 = 𝜋𝜌2 Dónde, 𝜌- radio de la circunferencia de la sección de entrada. 3.2.8 El cálculo grafo-analítico de una cámara espiral metálica por la ley de constancia de la velocidad media (𝑉𝑚𝑒𝑑 = 𝑐𝑜𝑛𝑠𝑡) se ejecuta en el siguiente orden: a) Es dado el ángulo 𝜑𝑖𝑜 ; b) Para el valor dado de 𝜑𝑖𝑜 se determina el caudal que corresponde a esta sección, con la ecuación: 𝑄𝑒𝑛𝑡 𝑜 𝑄𝑖 = 𝜑 345 𝑖 𝑄𝑒𝑛𝑡 = 𝑄 345 360 Por tanto, 𝑄𝑖 = 𝑄 𝑜 𝜑 360 𝑖 CONSTRUCCIONES HIDRÁULICAS MÁQUINAS HIDRÁULICAS IVAN CALERO HIDALGO c) A partir del valor obtenido de 𝑄𝑖 se determina el área de la sección 𝐹𝑖 con la ecuación: 𝐹𝑖 = d) 𝑄𝑖 𝑉𝑒𝑛𝑡 A partir del área encontrada se determina el radio de la espiral 𝜌𝑖 utilizando la ecuación: 𝐹𝑖 = 𝜋𝜌𝑖2 e) La distancia hasta el centro de la espiral 𝑎𝑖 y el radio externo de la espiral se determinan con las ecuaciones: 𝐷𝑜 𝑎𝑖 = + 𝜌𝑖 2 𝑅𝑖 = 𝑎𝑖 + 𝜌𝑖 = 𝐷𝑜 + 2𝜌𝑖 2 Dónde, 𝐷𝑜 - diámetro del lado externo del distribuidor o elemento direccional. Los resultados se presentan en una tabla. 𝜑𝑖𝑜 𝑄𝑖 , 𝑚3 ⁄𝑠 𝐹𝑖 . 𝑚2 𝐹𝑖 3,14 𝐹 𝑖 𝜌𝑖 = √3,14 , m APLICACIÓN PRÁCTICA: DIMENSIONAR UNA CÁMARA ESPIRAL METÁLICA 2𝜌𝑖 , m 𝑅𝑖 = m 𝐷𝑜 2 + 2𝜌𝑖 ,