SEMANA 23 - MATEMATICA
PROMOVEMOS EL USO RESPONSABLE DE
LOS RECURSOS EN LAS CONSTRUCCIONES
USANDO LA CIRCUNFERENCIA Y LA
PARÁBOLA
ACTIVIDAD DIA 3:
.
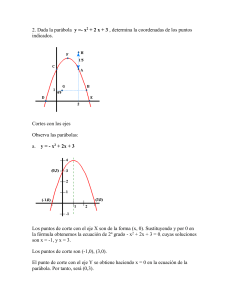
1.
El puente colgante Perene, tiene capacidad para soportar el
tránsito de vehículos de hasta 45 toneladas, facilitando así el
comercio de mercadería proveniente de la comunidad nativa de
Capachari con el distrito Pichanaqui. Se sabe que el puntal más
corto mide 5 m. (el puente tiene 102m de largo y unos pilares de
17 metros de altura)
¿Cuál será la altura donde está ubicado el cable a 32 m del pilar?
(x – h)2 = 4p (y – k)
En “V”:
+ 17
(x – 0)2 = 4p (y – 5)
P (51; 17)
--------------------------------------------------------17 m
Q (19; a)
X2 = 4p (y – 5)
17 m
En “P”:
512 = 4p (17 – 5)
V (0; 5)
- 51
(0; 0)
5m
P = 54,2
+ 51
+ 19
En “Q”:
192 = 4. (54,2)(a – 5)
32 m
01.
361 = 216,8(a – 5)
Utilizando la ecuación ordinaria de la parábola, se tiene:
102 m
Respuesta:
La altura será de 6,7m
SEMANA 23 - MATEMATICA
1.
En el siguiente gráfico se muestra un puente construido por una
municipalidad sobre una estructura con formas parabólicas
congruentes, que fueron evaluadas respecto a su resistencia
sísmica. El punto (6; 0) es de tangencia y la ecuación de la parábola
de la izquierda es 𝒙𝟐 − 𝟒𝒚.
¿Cuál es la ecuación de la parábola de la derecha?
Aplicamos la ecuación para
la parábola de la izquierda:
X2 = - 4 py
Pero el dato del problema:
X2 = - 4y
- 4py = - 4y
P=1
Aplicamos la ecuación para
la parábola de la derecha:
(x – h)2 = - 4p (y – k)
(x – 12)2 = - 4.1 (y – 0)
Respuesta:
La ecuación es (x – 12)2 = - 4y
SEMANA 23 - MATEMATICA
ACTIVIDAD DIA 4:
RESOLVEMOS PROBLEMAS HACIENDO USO DE
LAS ECUACIONES DE LA CIRCUNFERENCIA Y DE
LA PARÁBOLA EN DIVERSAS SITUACIONES.
1.
El parque zonal Huayna Cápac cuenta con
amplias áreas verdes, donde se puede
disfrutar de un buen paseo con toda la
familia. Se sabe que uno de los accesos del
ingreso principal al parque está formado
por dos partes, la parte inferior que mide
2 m de altura y 4 m de ancho y la parte
superior de forma parabólica que mide 2
m de altura y 4 m de ancho.
¿Cuál será la ecuación que represente el acceso del ingreso principal?
(H; k)
+4
Aplicamos la ecuación ordinaria
de la parábola:
(0; 4)
2 m
+2
----------------------
Q (2; 2)
(x – h)2 = - 4p (y – k)
(x – 0)2 = - 4p (y – 4)
2m
X2 = - 4p (y – 4)
Hallando “- 4p” en el punto Q:
-2
+2
22 = - 4p (2 – 4)
4 = - 4p (- 2)
4m
- 4p = - 2
Respuesta:
2
La ecuación es x = -2y
Reemplazo “4p” en la ecuación
ordinaria:
X2 = - 2 (y – 4)
y E {+ 2; + 4}
X=-2 v x=+2
y E {0; + 2}
SEMANA 23 - MATEMATICA
1.
Un municipio está a punto de inaugurar un túnel cuyo arco parabólico tiene
las siguientes dimensiones, 18 m de altura y 24 m de base. Se desea colocar
un reflector de mayor intensidad luminosa en la parte alta del túnel que está
ubicado a 8 m hacia la derecha de la base del centro del arco parabólico. ¿A
qué altura del túnel se ubicará dicho reflector?
Aplicamos la ecuación
ordinaria para la parábola:
(H; k)
(0; 18)
(x – h)2 = - 4p (y – k)
(x – 0)2 = - 4p (y – 18)
P (8; a)
A
X2 = - 4p (y – 18)
18 m
Hallando “- 4p”:
122 = - 4p (0 – 18)
(0; 0)
(- 12; 0)
(12; 0)
8
144 = - 4p (- 18)
- 4p = - 8
8m
Reemplazo “a” en el punto P:
82 = - 8 (a – 18)
24 m
64 = - 8 (a – 18)
Respuesta:
- 8 = a – 18
a = 10 m
Se ubicara a una altura de 10m
Un grupo de estudiantes presenta a las autoridades del distrito un proyecto
orientado a la construcción en la plaza de armas de una laguna artificial en
forma circular con un radio de 5 m y sobre ella un arco parabólico, en el cual
se pondrá el nombre del distrito en su punto máximo.
Las autoridades del distrito ordenan la ejecución de dicho proyecto, el mismo
que estará ubicado exactamente 12 m al este y 18 m al sur de la municipalidad
y el arco parabólico se ubicará entre los extremos sur y norte de la laguna
artificial y tendrá una altura de 10 m.
a) Calcula la ecuación general de la circunferencia
12
(0; 0)
X
Para hallar la ecuación general de la
circunferencia; partimos de su
ecuación ordinaria
(x – h)2 + (y – k)2 = r2
(x – 12)2 + (y + 18)2 = 52
X2 – 24x + 144 + y2 + 36y + 324 = 25
r=5
- 18
Respuesta:
La ecuación es
x – 24x + y2 + 36y + 443 = 0
2
SEMANA 23 - MATEMATICA
b) Calcula la ecuación general de la parábola
+ 10
V (0; 10)
Reemplazando “-4p” en
la ecuación ordinaria:
10 m
10 m
X2 = P (5; 0)
Sur
-5
Aplicamos la ecuación
para la parábola:
+5
Hallando “- 4p”
(x – h)2 = - 4p (y – k)
52 = - 4p (0 – 10)
(x – 0)2 = - 4p (y – 10)
25 = - 4p (- 10)
X2 = - 4p (y – 10)
1.
- 4p = -
5
2
(y – 10)
2x2 = - 5y + 50
X
Respuesta:
La ecuación es general es
2x2 + 5y – 50 = 0
5
2
Hace algunos años atrás, los habitantes de dos distritos tenían serios
problemas para comunicarse, e incluso tener acceso a productos de primera
necesidad les resultaba complicado. Esto llegó a su fin cuando se construyó
un túnel de forma parabólica, el cual presenta como altura máxima 4 m de
altura y tiene un ancho máximo de 12 m, facilitando así la mejor convivencia
entre las personas. Si el túnel tiene la forma de una parábola, calcular su
ecuación general.
Aplicamos la ecuación ordinaria para la
parábola:
(H; k)
(x – h)2 = - 4p (y – k)
(0; 4)
Hallamos -4p, en forma directa, usando
el punto del vértice y el punto p:
(6 – 0)2 = - 4p (0 – 4)
62 = - 4p (- 4)
4m
- 9 = - 4p
Remplazando en la ecuación ordinaria y
resolviendo:
(x – 0)2 = - 9 (y - 4)
X2 = -9y + 36
Q (- 6; 0)
P (6; 0)
x2 + 9y – 36 = 0
12 m
Respuesta:
La ecuación general es: x2 + 9y – 36 = 0
SEMANA 23 - MATEMATICA
v
SEMANA 23 - MATEMATICA
Me resulto mas fácil resolver las
situaciones que se parecían a las
clases anteriores.
Necesite más esfuerzo a las
situaciones
que
me
aparecieron
nuevos
o
complicados
Debo seguir mejorando en
practicar temas de parábola y
más de circunferencia
Mi compromiso es practicar mas
estos temas hasta que se me haga
fácil resolver un ejercicio como
estos
Me e sentido muy bien, con
mucho entusiasmo para seguir
practicando estos temas