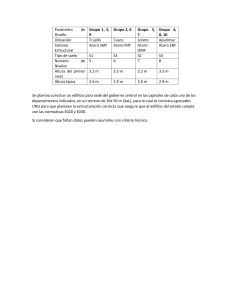
I El enfoque del diseño 1.1 DESARROLLO DE LOS PROCEDIMIENTOS DE DISE O POR ESFUERZO DE TRABAJO Y RESISTENCIA MAXIMA Varios de los primeros estudios sobre los miembros de concreto reforzado se basaron en teorias de resistencia máxima, por ejemplo, la teoría de la resistencia a la flexión de Thullie de 1897 y la teoría de la distribución parabólica de esfuerzos de Ritter de 1899. Sin embargo, alrededor de 1900 se aceptó en forma general la teoría de la línea recta (elástica) de Coignet y Ted,esco, en parte principalmente debido a que la teoría elástica era el mltodo convencional de diseño para otros materiales y en parte a que se pensaba que la variación lineal del esfuerzo conducía a una formulación matemática más sencilla. Además las pruebas habían mostrado que la utilización de la teoría elástica con valores elegidos cuidadosamente para los esfuerzos permisibles de trabajo conducía a una estructura que mos­ traba comportamiento satisfactorio bajo las cargas de servicio y que tenía un margen adecuado de seguridad contra el colapso. En consecuencia, la teoría elástica ha sido la base del diseño del concreto reforzado durante muchos años. Recientemente se ha renovado el interés en la teoría de la resistencia máxima como base del diseño. Después de más de medio siglo de expe­ riencia práctica y pruebas de laboratorio, conocemos mejor el compor­ tamiento del concreto estructural, a la vez que se han manifestado las deficiencias del método de diseño de la teoría elástica (esfuerzo de tra­ bajo). Esto ha dado como resultado un ajuste periódico al método de diseño por esfuerzo de trabajo, aunque cada vez es más evidente que el método de diseño se debe basar en las propiedades inelásticas reales del concreto y del acero. Por tanto, el diseño basado en la resistencia máxima se aceptó como una alternativa al diseño por esfuerzo de trabajo en los códigos de construcción para el concreto reforzado del Instituto Nor­ teamericano del Concreto (ACI) en 1956 y del Reino Unido en 1957. Se pueden resumir estos dos enfoques del disei\o como sigue: 1 2 El enfoque del disefto Diseño por esfuerzo de trabajo (teoría elástica) Las secciones de los miembros de la estructura se diseñan suponiendo una variación lineal para la relación esfuerzo - deformación lo que asegura que bajo las cargas de servicio los esfuerzos del acero y del concreto no ex­ ceden los esfuerzos permisibles de trabajo. Los esfuerzos permisibles se consideran como fracciones fijas de la resistencia máxima o de la resisten­ cia de cedencia de los materiales; por ejemplo, para la compresión por flexión se puede suponer 0.45 de la resistencia de cilindro del concreto. Los momentos tlexionantes y fuerzas que actúan en las estructuras es­ táticamente indeterminadas se calculan suponiendo comportamiento elás­ tico lineal. Diseño por resistencia máxima Las secciones de los miembros de las estructuras se diseñan tomando en cuenta las deformaciones inelásticas para alcanzar la resistencia máxima (o sea el concreto a la resistencia máxima y generalmente el acero en ceden­ cia) cuando se aplica una carga máxima a la estructura, igual a la suma de cada carga de servicio multiplicada por su factor respectivo de carga. Los factores típicos de carga utilizados en la práctica son 1.4 para la carga muerta y 1.7 para la carga viva. Los momentos flexionantes y fuerzas que actúan en las estructuras estáticamente indeterminadas bajo carga máxima se calculan suponiendo comportamiento elástico lineal de la estructura hasta la carga máxima. En forma alterna, los momentos flexionantes y fuerzas se calculan tomando parcialmente en cuenta la redistribución de las acciones que pueden ocurrir debido a las relaciones no lineales entre las acciones y deformaciones en los miembros bajo cargas elevadas. Algunas de las razones para la tendencia hacia el diseño por resistencia máxima son las siguientes: l . Las secciones de concreto reforzado se comportan inelásticamente bajo cargas elevadas, en consecuencia, la teoría elástica no puede dar una predicción segura de la resistencia máxima de los miembros, ya que las deformaciones inelásticas no se toman en consideración; en consecuencia, para las estructuras diseñadas por el método del esfuerzo de trabajo, se desconoce el factor exacto de carga (carga máxima/carga de servicio), el que varía de estructura a estructura. 2. El diseño por resistencia última permite una selección más racional de los factores de carga. Por ejemplo, se puede utilizar un factor de carga bajo para cargas conocidas con mayor precisión, tales como cargas muer­ tas, y un factor de carga más elevado para cargas conocidas con menos precisión, las cargas vivas por ejemplo. Desarrollo de los prottdimientos de diaeflo por esfuerzo de trabajo y resistencia mixima S 3. La curva esfuerzo-deformación para el concreto es no lineal y depende del tiempo. Por ejemplo, las deformaciones por flujo plástico para el concreto bajo esfuerzo sostenido constante pueden ser varias veces mayores que la deformación elástica inicial. En consecuencia, el valor de la relación modular (relación del módulo elástico del acero al del concreto) utilizada en el diseño por esfuerzo de trabajo es una aproximación burda. Las deformaciones por flujo plástico pueden provocar una redistribución apreciable del esfuerzo en las secciones de concreto reforzado, lo que im­ plica que los esfuerzos que existen realmente bajo.cargas de servicio a menudo tienen poca relación con los esfuerzos de diseño. Por ejemplo, el acero de compresión en las columnas puede alcanzar la resistencia de cedencia durante la aplicación prolongada de cargas de servicio, aunque este efecto no es evidente del análisis elástico si se utilizan los valores recomendados normalmente para la relación modular. El diseño por resis­ tencia máxima no requiere conocer la relación modular. 4. El diseño por resistencia max1ma utiliza reservas de resistencia resultantes de una distribución más eficiente de los esfuerzos permitidos por las deformaciones inelásticas, y en ocasiones indica que el método elástico es muy conservador. Por ejemplo, el acero de compresión en las vigas doblemente reforzadas por lo general alcanza la resistencia de ceden­ cia bajo carga máxima, y sin embargo, la teoría elástica puede indicar un esfuerzo bajo en este acero. 5. El diseño por resistencia máxima utiliza con mayor eficiencia el refuerzo de alta resistencia, y se pueden utilizar peraltes más pequeños en vigas sin acero de compresión. 6. El diseño por resistencia máxima permite al diseñador evaluar la ductilidad de la estructura en el rango inelástico. Este es un aspecto im­ portante cuando se considera la redistribución posible de los momentos de flexión en el diseño por cargas de gravedad y en el diseño por cargas sís­ micas o de explosiones. 1.2 DISE O POR RESISTENCIA Y SERVICIO En fechas más recientes se ha reconocido que el enfoque de diseño para el concreto reforzado debe idealmente combinar las mejores características de los diseños por resistencia máxima y por esfuerzo de trabajo, ya que, si solamente se proporcionan las secciones por los requerimientos de resis­ tencia máxima, hay el peligro de que aunque el factor de carga sea ade­ cuado, el agrietamiento y las deflexiones bajo cargas de servicio puedan ser excesivas. El agrietamiento puede ser excesivo si los esfuerzos en el acero son elevados o si las varillas están mal distribuidas. Las deflexiones 4 El enfoque del disei\o pueden ser críticas si se utilizan secciones de poco peralte, las que son posibles en el diseño por resistencia máxima, junto con esfuerzos elevados. En consecuencia, para garantizar un diseño satisfactorio, se deben com­ probar los anchos de las grietas y las deflexiones bajo cargas de servicio para asegurar que estén dentro de valores límites razonables, dictados por los requerimientos funcionales de la estructura. Esta comprobación re­ quiere utilizar la teoría elástica. En 1964, el Comité Europeo del Concreto dio sus recomendaciones para un código internacional de práctica para el concreto reforzado. Este documento presentó el concepto de diseño por estado límite, proponiendo que la estructura se diseñe con referencia a varios estados límites. Los es­ tados límites más importantes son: resistencia bajo carga máxima, de­ flexiones y anchos de grietas bajo carga de servicio. Este enfoque está ad­ quiriendo aceptación en muchos países. En consecuencia, la teoría de la resistencia máxima está convirtiendose en el enfoque prodominante para dimensionar las secciones, utilizando la teoría elástica solamente para asegurar el servicio. También cabe notar que la teoría de la resistencia máxima se ha utilizado para proporcionar secciones en la URSS y en al­ gunos otros países europeos desde hace varios años. Es probable que el uso del diseño por resistencia máxima se siga extendiendo, y parece que no transcurrirán muchos años antes de que se siga el ejemplo del Comité Europeo del Concreto y que desaparezca el método del esfuerzo de trabajo de los códigos de construcción para el concreto reforzado. Los códigos de construcción de 1956 y 1963 del Instituto Norteame­ ricano del Concreto permitían utilizar el método del esfuerzo de trabajo o el de la resistencia máxima. En cambio, el código1.2 de 1971 del ACI en­ fatiza el diseño en base a la resistencia con comprobaciones por servicio. Sin embargo, el código de 1971 también permite otro método de diseño en que se utiliza el esfuerzo de trabajo para disefiar vigas en flexión y ecuaciones de resistencia máxima factorizadas para diseñar miembros para las demás acciones. Es evidente que la única razón de permitir este método alterno ha sido el tratar de mantenerse dentro del marco general del diseño convencional. En este sentido, es probable que los códigos futuros del ACI omitan completamente este procedimiento alterno. También es interesante notar un cambio en la terminología en el código del ACI de 1971. Rara vez aparece la palabra "máxima". Por ejemplo, se escribe la palabra "resis­ tencia" en vez de "resistencia máxima." En este libro se adopta el enfoque de la resistencia y servicio del código de 1971 del ACI, debido a que se considera que enfatiza el comportamien­ to real del concreto reforzado y que es el enfoque más lógico para el di­ seño. Siempre que es posible, se describen los fundamentos de las reco­ mendaciones del código ACI. Cuando es necesario, se suplementan las recomendaciones del código a la luz de nuevos resultados de investtgación de que se dispone, y se proporciona cierta comparación con otros códigos. Deiarrollo de las procedimientos de diaeflo por esfuerzo de trabajo y reiiatencia miiima 5 1.3 METODO DE DISE80 POR RESISTENCIA Y SERVICIO DEL ACI 1.3.1 Recomendaciones sobre resistencia El código1.2 del ACI de 1971 separa las recomendaciones de resistencia para la seguridad estructural en dos partes: factores de carga y factores de reducción de capacidad. Factores de carga Los factores de carga tienen el propósito de dar seguridad adecuada contra un aumento en las cargas de servicio más allá de las especificadas en el diseño para que sea sumamente improbable la falla. Los•factores de carga tam­ bién ayudan a asegurar que las deformaciones bajo las cargas de servicio no sean excesivas. Los factores de carga utilizados para carga muerta, car­ ga viva, presión lateral de la tierra y de fluidos, cargas de viento y sismos, difieren en magnitud. Los factores de carga son distintos para diversos tipos de cargas debido a que, por ejemplo, es menos probable que la carga muerta de una estructura se exceda que la carga viva indicada. La carga máxima de la estructura debe ser igual por lo menos a la suma de cada car­ ga de servicio multiplicada por su factor respectivo de carga. El código ACI de 1971 recomienda que la resistencia requerida U para resistir la car­ ga muerta D y la carga viva L sea por lo menos igual a U = 1.4D + l.7L (1.1) Cuando se necesita considerar la carga de viento W en el diseño, la resis­ tencia requerida U debe ser por lo menos igual a U = 0.75(1.4D + l.7L + l.7W) (1.2) en que se deben considerar los casos en que L adquiera su valor total o cero, y U= 0.9D + 1.3W 1 . (1.3) cuando las acciones resultantes de D y W sean de signos opuestos. Si se necesita incluir la carga sísmica E, también se deben satisfacer las ecs. 1.2 y 1.3 sustituyendo l. lE por W. En el código se proporcionan los reque­ rimientos de resistencia para otros tipos de cargas. En la forma indicada, los factores de carga no varían con la gravedad de la consecuencia de la falla. Por ejemplo, se podría esperar que el factor de carga utilizado en un hospital fuera mayor que el utilizado para una fábrica. Sin embargo, se supone que las cargas prescritas de servicio in- 6 El enfoque del duefto cluyen el efecto de la gravedad de la falla. Sin embargo, los factores de carga establecidos deben considerarse como valores mínimos. Si las con­ secuencias de falla son especialmente graves o si no puede estimarse ra­ zonablemente la carga de servicio, es posible que sea conveniente emplear valores incrementados. Factores de reducción de capacidad Los factores de reducción de capacidad <p se proporcionan para tomar en cuenta inexactitudes en los cálculos y fluctuaciones en las resistencias del material, en la mano de obra y en las dimensiones. Cada uno de estos fac­ tores bien puede estar dentro de límites tolerables, pero combinados pueden producir menor capacidad en los elementos diseñados. La ecua­ ción básica de resistencia para una sección puede decirse que da la resis­ tencia ideal, siempre que la ecuación sea científicamente correcta, que los materiales tengan la resistencia especificada y que los tamafios sean como se muestran en los dibujos. La resistencia confiable de la sección a utilizar en los cálculos de disefio se considera como la resistencia ideal multipli­ cada por <p donde el valor del factor de reducción de capacidad <p depende de la importancia de las cantidades variables. Los valores recomendados por el código ACI de 1971 son: flexión, con o sin tensión axial o tensión axial <p = 0.90 flexión con compresión axial o compresión axial: <p = 0.75 si es reforzada con hélice en casos contrarios <p = O.70 (se puede aumentar linealmente <p hasta 0.9 para secciones con compresión axial pequeña que tienda a cero) <p = 0.85 cortante y torsión En el código se dan otros valores. Las variables adicionales que se han considerado para prescribir los factores de reducción de capacidad incluyen la seriedad de la consecuencia de la falla de los miembros respecto a toda la estructura, y el grado de ad­ vertencia implicito en el modo de falla. Las vigas tienen el más alto valor de <p debido a que están diseñadas para fallar en forma dúctil con cedencia del acero de tensión. Normalmente la advertencia de este tipo de falla se daría por considerable agrietamiento y grandes deflexiones, y ya que la variabilidad de la resistencia del acero es menor que la del concreto, se puede predecir con gran exactitud la resistencia a flexión. Las columnas tienen los valores más bajos de cp puesto que pueden fallar en modo frágil cuando la resistencia del concreto es el factor crítico. Adicionalmente, la falla de una columna puede significar el desplome de toda la estructura, y es difícil realizar la reparación de columnas. Las columnas reforzadas con hélice son más dúctibles que las de estribos, por lo que se les ha asignado un mayor valor de <p El valor de <p para cortante y torsión es intermedio, Desarrollo de l01 proc:edimientOI de diaefto por esfuerzo de trabajo y resistencia mixima 7 ya que la contribución del concreto a la resistencia es menos crítica que en el caso de miembros a compresión y la teoría que predice la resistencia es menos exacta que la correspondiente a la de flexión. La carga máxima en el diseño se calcula en base a la resistencia con­ fiable. En base a la resistencia ideal, el factor global de seguridad para una estructura cargada por carga muerta y viva es 1.4D + 1.7L 1 (1.4) D + L <P El factor global de seguridad respecto a la resistencia ideal de la sección (en el caso de flexión, con o sin tensión axial) varía desde 1.56 paraL/D = O hasta 1.82 para L/D = 4, en que el valor más alto se aplica apropia­ damente a las condiciones de mayor carga viva. Para miembros con flexión y compresión axial, el factor global de seguridad varía entre 2.00 y 2.34 para L/ D entre O y 4, lo que proporciona mayor seguridad global a un elemento estructural más crítico. La resistencia ideal se calcula utilizando las resistencias especificadas del concreto y del acero. Debido a que estos valores de resistencia normal­ mente se exceden en una estructura real, se dispone de una reserva adi­ cional de resistencia. 1.3.2 Recomendaciones sobre servicio La evaluación del comportamiento de la estructura bajo carga de servicio es una consideración.muy importante cuando los miembros se propor­ cionan en base a la resistencia requerida, lo que se debe a que los miem­ bros con pequeñas secciones y secciones con poco acero de compresión, pueden satisfacer los requerimientos de resistencia, pero conducen a esfuer­ zos y deformaciones elevados bajo carga de servicio. En consecuencia, se debe verificar que las deflexiones bajo carga de servicio estén dentro de los límites aceptables. El control del agrietamiento también es muy importante para fines de apariencia y durabilidad. En consecuencia, los anchos de las grietas bajo carga de servicio no deben exceder los límites especificados. Es difícil especificar límites aceptables para las deflexiones y los anchos d grieta; no obstante, en el código del ACI de 19711.2 se proporcionan recomendaciones para ambos. 1.3.3 Recomendaciones sobre ductilidad Una consideración importante adicional a la de resistencia y servicio es la de ductilidad. Es importante asegurar que en el caso extremo de que una estructura se cargue a la falla, ésta se comporte en forma dúctil. Esto sig­ nifica asegurar que la estructura no falle en forma frágil sin advertencia, sino que sea capaz de sufrir grandes deformaciones bajo cargas cercanas la máxima. Estas grandes deflexiones dan amplia advertencia de falla, y 8 El enfoque del dudo manteniendo la capacidad de transmisión de carga se puede impedir el desplome total y salvar vidas. Además el comportamiento dúctil de los miembros permite utilizar en el diseño redistribuciones de momentos fle­ xionantes que toman en cuenta la redistribución posible del patrón de momentos elásticos a flexión. En las áreas en que se requiere diseñar por carga sísmica, la ductilidad constituye una consideración de extrema importancia, debido a que la norma actual de los códigos para cargas sísmicas (v. gr. el código de Con­ es diseñar estructuras que sólo resistan elásticamen­ trucción Uniformeu te los sismos moderados; en el caso de sismos intensos se confía en la dis­ ponibilidad de suficiente ductilidad después de la cedencia para permitir a la estructura sobrevivir sin desplome. En consecuencia, las recomenda­ ciones para cargas sísmicas sólo se pueden justificar si la estructura tiene suficiente ductilidad para absorber y disipar energía mediante deforma­ ciones inelásticas cuando ella se sujeta a cargas cíclicas. Para asegurar el comportamiento dúctil, los diseñadores deben dar es­ pecial atención a los detalles, tales como cuantía de refuerzo longitudinal, anclaje del refuerzo y confinamiento del concreto comprimido, evitando así los tipos frágiles de falla (por ejemplo la falla debida a cortante).-El código ACI de 19711.2 hace recomendaciones acerca de la cuantía de acero longitudinal que produce secciones dúctiles, a la vez que permite cierta redistribución de los momentos flexionantes del diagrama de mo­ mentos elásticos. Adicionalmente y por primera vez, el código incluye un apéndice que da recomendaciones especiales para el diseño sísmico. 1.4 1.4.1 CONSIDERACIONES SOBRE RESISTENCIA DE LOS MIEMBROS Desarrollo de la r:esistencia de los miembros A menudo en el diseño es necesario evaluar los límites posibles superio. e inferior de la resistencia probable de las componentes estructurales. Esto es lo que sucede cuando se quiere lograr una secuencia específica en la ob­ tención de resistencia en los miembros de una estructura cargada a la falla. Por ejemplo, en una junta de viga-columna en un marco continuo, para evitar una falla de columna con sus posibles consecuencias catastróficas, siempre es conveniente que se desarrolle la resistencia de la viga antes que la resistencia de la columna. Evitar todos los tipos de falla no dúctil es una característica especial del di:;eño sísmico; consecuentemente, es importan­ te conocer la variación posible de las resistencias problables de los miem­ bros estructurales. Las estructuras reales contienen variaciones en las resistencias del con­ creto y acero respecto de los valores especificados, y hay desviaciones Desarrollo de 101 procedimient01 de disefto por esfuerzo de trabajo y resistencia mixima 9 inevitables en las medidas especificadas debido a tolerancias constructivas. Por otra parte, se han hecho ciertas suposiciones en la deducción de las ecuaciones de la resistencia, por lo que es difícil calcular con exactitud la resistencia real de una estructura; sin embargo, es posible definir niveles de resistencia probable de los miembros, las que se pueden utilizar en distin­ tos tipos de diseño. En las secciones siguientes se definen los niveles de resistencia ideal, resistencia confiable, resistencia probable y sobrerresis­ tencia. 1.4.2 Resistencia ideal S; La resistencia ideal o nominal de una sección de un miembro S; se obtiene teóricamente prediciendo el comportamiento de falla de la sección de la geometría supuesta de ésta y de las resistencias especificadas de los ma­ teriales. La mayor parte de este libro se ocupa de la deducción de la resis­ tencia ideal, con la que se pueden relacionar en forma conveniente otros niveles de resistencia. 1.4.3 Resistencia confiable Sd En las recomendaciones de resistencia descritas en la sección 1.3.1 se aclaró el propósito del factor q, de reducción de capacidad. El factor de reducción de capacidad permite relacionar la resistencia confiable Sd con la resistencia ideal mediante la expresión sd = q,S¡ (1.5) en que q,. el factor de reducción de capacidad, es menor que 1. 1.4.4 Resistencia probable SP La resistencia probable SP toma en consideración que las resistencias de los materiales generalmt:nte son mayores que las resistencias especificadas. Por ejemplo, la resistencia de cedencia del acero puede ser hasta 20% mayor que la especificada, y la del concreto hasta 30% o incluso superior a una edad mayor o si el material se comprime triaxialmente. Mediante pruebas rutinarias se pueden obtener las resistencias probables de los materiales, pruebas que normalmente se desarrollan durante la construc­ ción de la estructura. Si la información se requiere en la etapa de diseño ésta se debe basar en la experiencia previa tenida con los materiales. Se puede relacionar la resistencia probable con la resistencia ideal mediante la expresión SP = q,pS; (1.6, 10 El enfoque del disei\o en que <pP es el factor de resistencia probable que toma en consideración el hecho de que los materiales sean más fuertes que los especificados y es mayor que l. 1.4.5 Sobrerresistencia S0 La sobrerresistencia S 0 toma en cuenta todos los factores posibles que rueden provocar aumentos de resistencia; éstas incluyen una resistencia del acero más elevada que la de cedencia especificada más la resistencia adicional del acero debida al endurecimiento por deformación bajo gran­ des deformaciones, una resistencia del concreto más elevada que la es­ pecificada, tamaños de secciones más grandes que los supuestos, com­ presión axial en los miembros a flexión debida a restricción lateral, y refuerzo adicional impuesto para fines constructivos y que no se toma en cuenta en los cálculos. Se puede relacionar la sobrerresistencia con la resistencia ideal mediante la expresión = <pºS; Sº (1.7) en que <p0 es el factor de sobrerresistencia que toma en consideración todas las fuentes de aumento de resistencia y es mayor que 1. 1.4.6 Relaciones entre distintas resistencias El más alto nivel de protección para asegurar que la componente A, que recibe carga de la componente B, no falle antes de que se desarrolle la resistencia de la componente B, se obtiene cuando la resistencia confiable de la componente A excede la sobrerresistencia de la componente B, SdA ;;::: soB· La relación siA ;;::: soB• proporciona un nivel más bajo de protección y la relación SpA;;::: S08. proporciona un nivel todavía más bajo de protec­ ción. La mejor forma de expresar el grado de protección que dan estos · casos es mediante la relación de las resistencias probables, SpA/SpB• de las dos componentes. Para los anteriores niveles de protección, de alto a bajo, se encuentra a partir de las ecuaciones 1.5 a 1.7 que: S dA= SoB 0. SoB = <p AS pA/ <p pA ;;::, } <poBSpB/<ppB >- <ppA'PoB SpB ,_,- <ppB<fJA (1.8a) SPA/<P¡,_A - ;;::: <fJoBSpB/<fJpB >- <fJ¡,_A'PoB SpB ,_,., <fJpB ( 1.8b) = SpA SoB <fJoBSpB/ <fJ pB 1 ?- 1 <fJoB SpB <ppB ( 1.8c) Desarrollo de loe prottdimientoe de dudio por esfuerzo de trabajo y resistencia mb:ima 11 Por ejemplo, si <pA = 0.9, <fJpA = <fJpB = 1.1, y <p08 = 1.3, las relaciones de la resistencia probable de la componente A a la resistencia probable de la componente B necesarias para asegurar que la componente B no falle son (1.1 x 1.3)/(1.1 x 0.9) = 1.44, 1.1 x 1.3/1.1 = 1.30, y 1.3/1.1 = 1.18, de acuerdo con las ecuaciones 1.8a, 1.8b y 1.8c respectivamente, que in­ dican los distintos niveles de protección para la componente B. 1.5 BIBLIOGRAFIA 1.1 CEB, "Recommendations for an lnternátional Code of Practice for Reinfor­ ccd Concrete," Comité Européen du Beton (CEB), París, 1964. (La Cement and Concrete Association de Londres dispone de una traducción al ingles) 1.2 ACI Committee 318, "Building Code Requirements for Reinfored Concrete (ACI 318-71)." American Concrete lnstitute, Detroit, 1971, pág. 78. 1.3 ICBO, "Uniform Building Code," edición 1970, Vol. l, lnternational Con­ ference of Building Officials, Pasadena, Calif., pág. 651 pp.