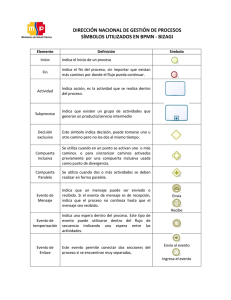
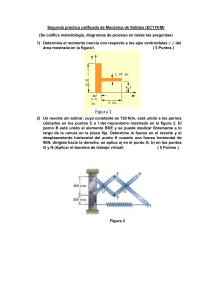
UNIVERSIDAD DE PANAMÁ FACULTAD DE INFORMATICA, ELECTRÓNICA Y COMUNICACIÓN INGENIERÍA MECTRÓNICA ELECTRÓNICA DIGITAL LABORATORIO #6 COMPARADOR DE MAGNITUD ESTUDIANTE: JOSÉ SIMMONDS GRUPO: M2-3 PROFESOR: VÍCTOR WILLIAMS FECHA DE ENTREGA: MIÉRCOLES, 30 DE NOVIEMBRE DE 2022 INTRODUCCIÓN En el presente informe de laboratorio se exhibe la implementación y análisis del circuito digital comparador de magnitud de dos (2) y cuatro (4) bits, empleando compuertas lógicas XOR, AND y NOT y circuitos integrados comerciales para el armado y utilizando LEDs para el análisis de los circuitos. El comparador de magnitud forma parte de los circuitos aritméticos, estos posibilitan las operaciones de cálculo en la tecnología digital y representan la base para el desarrollo de los sistemas computacionales. El desarrollo de los circuitos aritméticos se realiza a partir de la combinación adecuada de puertas lógicas, lo que implica una gran rapidez en el cálculo. Un comparador de magnitud es un circuito lógico combinacional que compara dos cantidades binarias de entrada y genera salidas para indicar cuál tiene la mayor magnitud. Un comparador de magnitud de 4 bits realiza la comparación de códigos binarios rectos o BCD. Se toman tres decisiones completamente decodificadas sobre dos palabras de 4 bits (A, B) y están disponibles externamente en tres salidas. Estos dispositivos son totalmente ampliables a cualquier número de bits sin necesidad de puertas externas. Se pueden comparar palabras de mayor longitud conectando los comparadores en cascada. Las salidas 𝐴 > 𝐵, 𝐴 < 𝐵 𝑦 𝐴 = 𝐵 de una etapa que maneja los bits menos significativos se conectan a las entradas correspondientes de la siguiente etapa que maneja los bits más significativos. La etapa que maneja los bits menos significativos debe tener una tensión de alto nivel aplicada a la entrada A = B. La ruta en cascada se implementa con un retardo de dos puertas para reducir el tiempo total de comparación en el caso de palabras largas. para palabras largas. OBJETIVOS Objetivos Generales: • Utilizar los conocimientos adquiridos en las experiencias de laboratorio anteriores e interconectar circuitos integrados que ejecutan funciones lógicas. Se utilizarán las compuertas AND, XOR y NOT, mediante la utilización de circuitos integrados comerciales, tales como: el 74LS85, para la implementación de comparadores de magnitud de dos (2) bit y cuatro (4) bits, de tal manera que el estudiante comprenda el funcionamiento de un comparador de digital de magnitud y vaya adquiriendo experiencia en la simulación de circuitos lógicos. Objetivos específicos: • • • Analizar y describir el funcionamiento de los circuitos de comparador de magnitud utilizando las funciones lógicas AND, XOR y NOT Uso de las compuertas lógicas AND, XOR y NOT, emplear bloques lógicos comerciales para la implementación de circuitos de comparador de magnitud de cuatro (4) bits Mostrar las relaciones y el comportamiento de las entradas y salidas para las funciones lógicas AND, XOR y NOT en circuitos de comparador de magnitud MATERIALES Para realizar esta experiencia se utilizaron los siguientes materiales: 1. Un multímetro 2. 3. 4. 5. 6. 7. 8. Tres (3) LEDs Un circuito integrado 7485 o 74LS85 Un circuito integrado 74LS04 Un circuito integrado 74LS08 Un circuito integrado 74LS86 Una fuente de DC de 5V Software “Multisim” y “Proteus 8 profesional” PROCEDIMIENTO I. Circuito Comparador de dos (2) bits Para el estudio del funcionamiento de un circuito comparador digital de 2 bits, se implementó el circuito que se presenta en la FIG. 1, y según las simulaciones obtenidas se completó la tabla de verdad (TABLA No.1). FIG. 1 A = 0V y B = 0V En el análisis de la salida A < B se observó que cuando la entrada de la primera compuerta NOT es A = 0, su salida es 1 lógico, ya que la salida de una compuerta NOT es siempre el valor opuesto del valor de la entrada, esta salida es la entrada de la primera compuerta AND, la cual tiene como segunda entrada el valor de B = 0, por lo cual la salida de esta compuerta AND es 0, ya que la salida de una compuerta AND es 0, si una de sus entradas ̅B = 0̅ ∙ 0 = 1 ∙ 0 = 0. Para son 0, por lo tanto, la salida de A < B es 0, ya que (A < B) = A la salida A = B, se tiene una compuerta XOR, el cual sus valores de entrada eran A = 0 y B = 0, por lo tanto, su salida fue 0, esta salida, era la entrada para la segunda compuerta NOT, haciendo que la salida fuese 1, ya que la salida de una compuerta NOT es el valor contrario al de su entrada, por lo tanto, la salida de A = B fue 1, ya que (A = B) = ̅̅̅̅̅̅̅̅ A⊕B= ̅̅̅̅̅̅̅̅ 0 ⊕ 0 = 0̅ = 1 . Y finalmente para la salida A > B se tiene a la tercera compuerta NOT, que tiene como entrada B = 0, por lo cual la salida de esta compuerta es 1, ya que la compuerta NOT su salida evalúa al valor contrario al de valor de entrada, esta salida, es la entrada para la segunda compuerta AND que tiene como entrada A = 0, por lo cual la salida de esta compuerta AND es 0, ya que la salida de una compuerta AND es 0, si cualquiera de sus ̅ = 0∙1= 0 entradas son 0, por lo cual la salida (A > B) es 0, ya que (A > B) = AB 𝐴 = 0𝑉 𝑦 𝐵 = 5𝑉 En el análisis de la salida A < B se observó que cuando la entrada de la primera compuerta NOT es 𝐴 = 0, su salida es 1, ya que la salida de una compuerta NOT es siempre el valor opuesto del valor de la entrada, esta salida es la entrada de la primera compuerta AND, la cual tiene como segunda entrada el valor de 𝐵 = 5, por lo cual la salida de esta compuerta AND es 1 lógico, ya que la salida de una compuerta AND es 1 cuando ambas entradas son 1, por lo tanto, la salida de 𝐴 < 𝐵 es 1, ya que (𝐴 < 𝐵) = 𝐴̅𝐵 = 0̅ ∙ 1 = 1 ∙ 1 = 1. Para la salida 𝐴 = 𝐵, se tiene una compuerta XOR, el cual sus valores de entrada eran 𝐴 = 0 𝑦 𝐵 = 5, por lo tanto, su salida fue 1, ya que la salida de una compuerta XOR es 1, siempre que sus valores de entrada se encuentran en niveles diferentes, esta salida, era la entrada para la segunda compuerta NOT, haciendo que la salida fuese 0, ya que la salida de una compuerta NOT es el valor contrario al de su entrada, por lo tanto, la salida de 𝐴 = 𝐵 fue 0, ya que (𝐴 = 𝐵) = ̅̅̅̅̅̅̅̅ 𝐴 ⊕ 𝐵 = ̅̅̅̅̅̅̅̅ 0 ⊕ 1 = 1̅ = 0 . Y finalmente para la salida 𝐴 > 𝐵 se tiene a la tercera compuerta NOT, que tiene como entrada 𝐵 = 5, por lo cual la salida de esta compuerta es 0, ya que la compuerta NOT su salida evalúa al valor contrario al de valor de entrada, esta salida, es la entrada para la segunda compuerta AND que tiene como entrada 𝐴 = 0, por lo cual la salida de esta compuerta AND es 0, ya que la salida de una compuerta AND es 0, si cualquiera de sus entradas son 0, por lo cual la salida (𝐴 > 𝐵) es 0, ya que (𝐴 > 𝐵) = 𝐴𝐵̅ = 0 ∙ 1̅ = 0 ∙ 0 = 0 𝐴 = 5V 𝑦 𝐵 = 0V En el análisis de la salida A < B se observó que cuando la entrada de la primera compuerta NOT es A = 5, su salida es 0 lógico, ya que la salida de una compuerta NOT es siempre el valor opuesto del valor de la entrada, esta salida es la entrada de la primera compuerta AND, la cual tiene como segunda entrada el valor de B = 0, por lo cual la salida de esta compuerta AND es 0, ya que la salida de una compuerta AND es 0, si una de sus entradas ̅B = 1̅ ∙ 0 = 0 ∙ 0 = 0. Para son 0, por lo tanto, la salida de A < B es 0, ya que (A < B) = A la salida A = B, se tiene una compuerta XOR, el cual sus valores de entrada eran A = 5 y B = 0, por lo tanto, su salida fue 1, ya que la salida de una compuerta XOR es 1 siempre que sus valores de entrada se encuentren en niveles diferentes, esta salida, era la entrada para la segunda compuerta NOT, haciendo que la salida fuese 0, ya que la salida de una compuerta NOT es el valor contrario al de su entrada, por lo tanto, la salida de A = B fue 0, ya que (A = B) = ̅̅̅̅̅̅̅̅ A ⊕ B = ̅̅̅̅̅̅̅̅ 1 ⊕ 0 = 1̅ = 0 . Y finalmente para la salida A > B se tiene a la tercera compuerta NOT, que tiene como entrada B = 0, por lo cual la salida de esta compuerta es 1, ya que la compuerta NOT su salida evalúa al valor contrario al de valor de entrada, esta salida, es la entrada para la segunda compuerta AND que tiene como entrada A = 5, por lo cual la salida de esta compuerta AND es 1, ya que la salida de una compuerta AND es 1, si ambas de sus entradas son 1, por lo cual la salida (A > B) es 1, ya que ̅ = 1 ∙ 0̅ = 1 ∙ 1 = 1 (A > B) = AB 𝐴 = 5V 𝑦 𝐵 = 5V En el análisis de la salida A < B se observó que cuando la entrada de la primera compuerta NOT es A = 5, su salida es 0 lógico, ya que la salida de una compuerta NOT es siempre el valor opuesto del valor de la entrada, esta salida es la entrada de la primera compuerta AND, la cual tiene como segunda entrada el valor de B = 5, por lo cual la salida de esta compuerta AND es 0, ya que la salida de una compuerta AND es 0, si una de sus entradas ̅B = 1̅ ∙ 1 = 0 ∙ 1 = 0. Para son 0, por lo tanto, la salida de A < B es 0, ya que (A < B) = A la salida A = B, se tiene una compuerta XOR, el cual sus valores de entrada eran A = 5 y B = 5, por lo tanto, su salida fue 0, ya que la salida de una compuerta XOR es 0 siempre que sus valores de entrada NO se encuentren en niveles diferentes, esta salida, era la entrada para la segunda compuerta NOT, haciendo que la salida fuese 1, ya que la salida de una compuerta NOT es el valor contrario al de su entrada, por lo tanto, la salida de A = B fue 1, ya que (A = B) = ̅̅̅̅̅̅̅̅ A ⊕ B = ̅̅̅̅̅̅̅̅ 1 ⊕ 1 = 0̅ = 1 . Y finalmente para la salida A > B se tiene a la tercera compuerta NOT, que tiene como entrada B = 5, por lo cual la salida de esta compuerta es 0 lógico, ya que la compuerta NOT su salida evalúa al valor contrario al de valor de entrada, esta salida, es la entrada para la segunda compuerta AND que tiene como entrada A = 5, por lo cual la salida de esta compuerta AND es 0, ya que la salida de una compuerta AND es 0, si cualquiera de sus entradas es 0, por lo cual la salida (A > B) es 0, ̅ = 1 ∙ 1̅ = 1 ∙ 0 = 0 ya que (A > B) = AB TABLA No. 1 A B A>B A=B A<B 0V 0V 0V 5V 0V 0V 5V 0V 0V 5V 5V 0V 5V 0V 0V 5V 5V 0V 5V 0V TABLA No. 1 (En niveles lógicos) A B A>B A=B A<B 0 0 0 1 0 0 1 0 0 1 1 0 1 0 0 1 1 0 1 0 II. Comparador digital de cuatro (4) bits En esta parte de la experiencia, pasamos a estudiar el funcionamiento de un comparador digital de 4 bits, para lo cual utilizamos el C.I. 7585 o 74LS85. Para esto, se procedió a implementar el circuito que se presenta en la FIG. 2, y luego se procedió a completar la tabla de verdad (TABLA No.2) según las simulaciones obtenidas. Observación: Se utilizo el software Proteus 8 profesional, para un mejor funcionamiento e implementación del circuito. (problemas técnicos con Multisim, al momento de cargar los C.I) FIG. 2 𝐴3 > 𝐵3 Según el diagrama de la figura 3, en el análisis de la salida 𝐴 > 𝐵, se observó que cuando la condición de entrada era 𝐴3 > 𝐵3, en donde en el circuito del diagrama lógico mostrado en la figura 3, el cual estaba conformado por una compuerta NAND, dos compuertas AND y una compuerta NOR , en donde los pines de entrada: A3=15 y B3=1,tomando como nivel lógico 𝐴3 = 1 𝑦 𝐵3 = 0, y según la condición de entrada, se ̅̅̅̅ + ̅̅̅̅̅̅̅̅̅̅̅̅ ̅̅̅̅ + ejecuta la operación de la siguiente forma:(𝐴 > 𝐵) = 𝐴3𝐵3 𝐴3 ⊕ 𝐵3 𝐴2𝐵2 ̅̅̅̅̅̅̅̅̅̅̅̅ ̅̅̅̅ + ̅̅̅̅̅̅̅̅̅̅̅̅ ̅̅̅̅ , en donde los valores 𝐴3 ⊕ 𝐵3 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴2 ⊕ 𝐵2 𝐴1𝐵1 𝐴3 ⊕ 𝐵3 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴2 ⊕ 𝐵2 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴1 ⊕ 𝐵1 𝐴0𝐵0 A2,B2,A1,B1,A0 y B0, son “Dont Care” (No importa), por lo tal la salida fue 1 para A>B, ya que ̅̅̅̅ + ̅̅̅̅̅̅̅̅̅̅̅̅ ̅̅̅̅ + ̅̅̅̅̅̅̅̅̅̅̅̅ ̅̅̅̅ + (𝐴 > 𝐵) = 𝐴3𝐵3 𝐴3 ⊕ 𝐵3 𝐴2𝐵2 𝐴3 ⊕ 𝐵3 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴2 ⊕ 𝐵2 𝐴1𝐵1 ̅̅̅̅̅̅̅̅̅̅̅̅ ̅̅̅̅ = 1 ∙ 0̅ + ̅̅̅̅̅̅̅̅ 𝐴3 ⊕ 𝐵3 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴2 ⊕ 𝐵2 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴1 ⊕ 𝐵1 𝐴0𝐵0 1 ⊕ 0 0 ∙ 0̅ + ̅̅̅̅̅̅̅̅ 1 ⊕ 0 ̅̅̅̅̅̅̅̅ 0 ⊕ 0 0 ∙ 0̅ + ̅̅̅̅̅̅̅̅ 1 ⊕ 0 ̅̅̅̅̅̅̅̅ 0 ⊕ 0 ̅̅̅̅̅̅̅̅ 0 ⊕ 0 0 ∙ 0̅ = 1 + 0 + 0 + 0 = 1, esta salida 1 lógico “ALTO”, se puede observar mediante el encendido de la LED de color amarillo, en la ilustración de la simulación realizada. 𝐴3 < 𝐵3 Según el diagrama de la figura 3, en el análisis de la salida 𝐴 < 𝐵, se observó que cuando la condición de entrada era 𝐴3 < 𝐵3, en donde en el circuito del diagrama lógico mostrado en la figura 3, el cual estaba conformado por una compuerta NAND, dos compuertas AND y una compuerta NOR , en donde los pines de entrada: A3=15 y B3=1, tomando como nivel lógico A3=0 y B3=1, y según la condición de entrada, se ejecuta la operación de la siguiente forma:(𝐴 < 𝐵) = ̅̅̅̅̅ 𝐴3 ∙ 𝐵3 + ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴3 ⊕ 𝐵3 ̅̅̅̅̅ 𝐴2 ∙ 𝐵2 + ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴3 ⊕ 𝐵3 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴2 ⊕ 𝐵2 ̅̅̅̅̅ 𝐴1 ∙ 𝐵1 + ̅̅̅̅̅̅̅̅̅̅̅̅ ̅̅̅̅ ∙ 𝐵0 , en donde los valores A2,B2,A1,B1,A0 y B0, son “Dont 𝐴3 ⊕ 𝐵3 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴2 ⊕ 𝐵2 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴1 ⊕ 𝐵1 𝐴0 Care” (No importa), por lo tal la salida fue 1 para 𝐴 < 𝐵, ya que (𝐴 < 𝐵) = ̅̅̅ 0∙1+ ̅̅̅̅̅̅̅̅ 0 ⊕ 1 ̅̅̅ 0 ∙ 0 + ̅̅̅̅̅̅̅̅ 0 ⊕ 1 ̅̅̅̅̅̅̅̅ 0 ⊕ 0 ̅̅̅ 0 ∙ 0 + ̅̅̅̅̅̅̅̅ 0 ⊕ 1 ̅̅̅̅̅̅̅̅ 0 ⊕ 0 ̅̅̅̅̅̅̅̅ 0 ⊕ 0 0̅ ∙ 0 = 1 + 0 + 0 + 0 = 1 , esta salida 1 lógico “ALTO”, se puede observar mediante el encendido de la LED de color verde, en la ilustración de la simulación realizada. 𝐴3 = 𝐵3 𝑦 𝐴2 > 𝐵2 Se observo que para la condición 𝐴3 = 𝐵3, es decir 𝐴3 = 1 𝑦 𝐵3 = 1, su salida se puede verificar mediante la siguiente forma: (𝐴 = 𝐵) = ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴3 ⊕ 𝐵3 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴2 ⊕ 𝐵2 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴1 ⊕ 𝐵1 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴0 ⊕ 𝐵0 = ̅̅̅̅̅̅̅̅ 1 ⊕ 1 ̅̅̅̅̅̅̅̅ 1 ⊕ 0 ̅̅̅̅̅̅̅̅ 0 ⊕ 0 ̅̅̅̅̅̅̅̅ 0 ⊕ 0 = 1 ∙ 0 ∙ 1 ∙ 1 = 0, por lo tanto, la salida de 𝐴3 = 𝐵3 es 0 “LOW" y para la condición 𝐴2 > 𝐵2, es decir 𝐴2 = 1 𝑦 𝐵2 = 0, su salida se puede verificar de la siguiente forma: ̅̅̅̅ + ̅̅̅̅̅̅̅̅̅̅̅̅ ̅̅̅̅ + ̅̅̅̅̅̅̅̅̅̅̅̅ ̅̅̅̅ + (𝐴 > 𝐵) = 𝐴3𝐵3 𝐴3 ⊕ 𝐵3 𝐴2𝐵2 𝐴3 ⊕ 𝐵3 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴2 ⊕ 𝐵2 𝐴1𝐵1 ̅̅̅̅̅̅̅̅̅̅̅̅ ̅̅̅̅ = 1 ∙ 1̅ + ̅̅̅̅̅̅̅̅ 𝐴3 ⊕ 𝐵3 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴2 ⊕ 𝐵2 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴1 ⊕ 𝐵1 𝐴0𝐵0 1 ⊕ 1 1 ∙ 0̅ + ̅̅̅̅̅̅̅̅ 1 ⊕ 1 ̅̅̅̅̅̅̅̅ 1 ⊕ 0 0 ̅̅̅ ∙0+ ̅̅̅̅̅̅̅̅ 1 ⊕ 1 ̅̅̅̅̅̅̅̅ 1 ⊕ 0 ̅̅̅̅̅̅̅̅ 0 ⊕ 0 0 ̅̅̅ ∙ 0 = 0 + 1 + 0 + 0 = 1, por lo tanto la salida A>B es 1 “HIGH”, esta salida se puede observar mediante la led de color amarillo en la ilustración de la simulación. 𝐴3 = 𝐵3 𝑦 𝐴2 < 𝐵2 Se observo que para la condición 𝐴3 = 𝐵3, es decir 𝐴3 = 1 𝑦 𝐵3 = 1, su salida se puede verificar mediante la siguiente forma: (𝐴 = 𝐵) = ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴3 ⊕ 𝐵3 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴2 ⊕ 𝐵2 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴1 ⊕ 𝐵1 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴0 ⊕ 𝐵0 = ̅̅̅̅̅̅̅̅ 1 ⊕ 1 ̅̅̅̅̅̅̅̅ 1 ⊕ 0 ̅̅̅̅̅̅̅̅ 0 ⊕ 0 ̅̅̅̅̅̅̅̅ 0 ⊕ 0 = 1 ∙ 0 ∙ 1 ∙ 1 = 0, por lo tanto, la salida de 𝐴3 = 𝐵3 es 0 “LOW" y para la condición 𝐴2 < 𝐵2, es decir 𝐴2 = 0 𝑦 𝐵2 = 1, su salida se puede verificar de la siguiente forma: (𝐴 < 𝐵) = ̅̅̅̅̅ 𝐴3 ∙ 𝐵3 + ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴3 ⊕ 𝐵3 ̅̅̅̅̅ 𝐴2 ∙ 𝐵2 + ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴3 ⊕ 𝐵3 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴2 ⊕ 𝐵2 ̅̅̅̅̅ 𝐴1 ∙ 𝐵1 + ̅̅̅̅̅̅̅̅̅̅̅̅ ̅̅̅̅ ∙ 𝐵0 = ̅̅̅ 𝐴3 ⊕ 𝐵3 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴2 ⊕ 𝐵2 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴1 ⊕ 𝐵1 𝐴0 1 ∙ 1 + ̅̅̅̅̅̅̅̅ 1 ⊕ 1 ̅̅̅ 0 ∙ 1 + ̅̅̅̅̅̅̅̅ 1 ⊕ 1 ̅̅̅̅̅̅̅̅ 0 ⊕ 1 ̅̅̅ 0∙0+ ̅̅̅̅̅̅̅̅ 1 ⊕ 1 ̅̅̅̅̅̅̅̅ 0 ⊕ 1 ̅̅̅̅̅̅̅̅ 0 ⊕ 0 0̅ ∙ 0 = 0 + 1 + 0 + 0 = 1, por lo tanto la salida 𝐴 < 𝐵 es 1 “HIGH”, esta salida se puede observar mediante la led de color verde en la ilustración de la simulación. 𝐴3 = 𝐵3, 𝐴2 = 𝐵2 𝑦 𝐴1 > 𝐵1 Se observo que para la condición 𝐴3 = 𝐵3, es decir 𝐴3 = 1 𝑦 𝐵3 = 1, su salida se puede verificar mediante la siguiente forma: (𝐴 = 𝐵) = ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴3 ⊕ 𝐵3 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴2 ⊕ 𝐵2 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴1 ⊕ 𝐵1 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴0 ⊕ 𝐵0 = ̅̅̅̅̅̅̅̅ 1 ⊕ 1 ̅̅̅̅̅̅̅̅ 1 ⊕ 0 ̅̅̅̅̅̅̅̅ 0 ⊕ 0 ̅̅̅̅̅̅̅̅ 0 ⊕ 0 = 1 ∙ 0 ∙ 1 ∙ 1 = 0, por lo tanto, la salida de 𝐴3 = 𝐵3 es 0 “LOW", para la condición 𝐴2 = 𝐵2, donde 𝐴2 = 1 𝑦 𝐵2 = 1, se obtiene una salida igual, es decir 𝐴2 = 𝐵2 es 0 “LOW”, y para la condición 𝐴1 > 𝐵1, donde los valores de 𝐴1 = 1 y 𝐵1 = 0, ̅̅̅̅ + ̅̅̅̅̅̅̅̅̅̅̅̅ ̅̅̅̅ + su salida se puede verificar de la siguiente forma: (𝐴 > 𝐵) = 𝐴3𝐵3 𝐴3 ⊕ 𝐵3 𝐴2𝐵2 ̅̅̅̅̅̅̅̅̅̅̅̅ ̅̅̅̅ + ̅̅̅̅̅̅̅̅̅̅̅̅ ̅̅̅̅ = 1 ∙ 1̅ + ̅̅̅̅̅̅̅̅ 𝐴3 ⊕ 𝐵3 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴2 ⊕ 𝐵2 𝐴1𝐵1 𝐴3 ⊕ 𝐵3 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴2 ⊕ 𝐵2 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴1 ⊕ 𝐵1 𝐴0𝐵0 1 ⊕ 1 1 ∙ 0̅ + ̅̅̅̅̅̅̅̅ 1 ⊕ 1 ̅̅̅̅̅̅̅̅ 1 ⊕ 0 0 ̅̅̅ ∙ 0 + ̅̅̅̅̅̅̅̅ 1 ⊕ 1 ̅̅̅̅̅̅̅̅ 1 ⊕ 0 ̅̅̅̅̅̅̅̅ 0 ⊕ 0 0 ̅̅̅ ∙ 0 = 0 + 1 + 0 + 0 = 1, esta salida se puede observar mediante la LED de color amarillo en la ilustración de la simulación. 𝐴3 = 𝐵3, 𝐴2 = 𝐵2 𝑦 𝐴1 < 𝐵1 Se observo que para la condición 𝐴3 = 𝐵3, es decir 𝐴3 = 1 𝑦 𝐵3 = 1, su salida se puede verificar mediante la siguiente forma: (𝐴 = 𝐵) = ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴3 ⊕ 𝐵3 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴2 ⊕ 𝐵2 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴1 ⊕ 𝐵1 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴0 ⊕ 𝐵0 = ̅̅̅̅̅̅̅̅ 1 ⊕ 1 ̅̅̅̅̅̅̅̅ 1 ⊕ 0 ̅̅̅̅̅̅̅̅ 0 ⊕ 0 ̅̅̅̅̅̅̅̅ 0 ⊕ 0 = 1 ∙ 0 ∙ 1 ∙ 1 = 0, por lo tanto, la salida de 𝐴3 = 𝐵3 es 0 “LOW", para la condición 𝐴2 = 𝐵2, donde 𝐴2 = 1 𝑦 𝐵2 = 1, se obtiene una salida igual, es decir 𝐴2 = 𝐵2 es 0 “LOW”, y para la condición 𝐴1 < 𝐵1, donde los valores de 𝐴1 = 0 y 𝐵1 = 1, su salida se puede verificar de la siguiente forma: (𝐴 < 𝐵) = ̅̅̅̅̅ 𝐴3 ∙ 𝐵3 + ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴3 ⊕ 𝐵3 ̅̅̅̅̅ 𝐴2 ∙ 𝐵2 + ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴3 ⊕ 𝐵3 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴2 ⊕ 𝐵2 ̅̅̅̅̅ 𝐴1 ∙ 𝐵1 + ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴3 ⊕ 𝐵3 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴2 ⊕ 𝐵2 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴1 ⊕ 𝐵1 ̅̅̅̅ 𝐴0 ∙ 𝐵0 = ̅̅̅ 1 ∙ 1 + ̅̅̅̅̅̅̅̅ 1 ⊕ 1 ̅̅̅ 0∙1+ ̅̅̅̅̅̅̅̅ 1 ⊕ 1 ̅̅̅̅̅̅̅̅ 0 ⊕ 1 ̅̅̅ 0 ∙ 0 + ̅̅̅̅̅̅̅̅ 1 ⊕ 1 ̅̅̅̅̅̅̅̅ 0 ⊕ 1 ̅̅̅̅̅̅̅̅ 0 ⊕ 0 0̅ ∙ 0 = 0 + 1 + 0 + 0 = 1, esta salida se puede observar mediante la LED de color verde en la ilustración de la simulación. 𝐴3 = 𝐵3, 𝐴2 = 𝐵2, 𝐴1 = 𝐵1 𝑦 𝐴0 > 𝐵0 Se observo que para la condición 𝐴3 = 𝐵3, es decir 𝐴3 = 1 𝑦 𝐵3 = 1, su salida se puede verificar mediante la siguiente forma: (𝐴 = 𝐵) = ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴3 ⊕ 𝐵3 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴2 ⊕ 𝐵2 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴1 ⊕ 𝐵1 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴0 ⊕ 𝐵0 = ̅̅̅̅̅̅̅̅ 1 ⊕ 1 ̅̅̅̅̅̅̅̅ 1 ⊕ 0 ̅̅̅̅̅̅̅̅ 0 ⊕ 0 ̅̅̅̅̅̅̅̅ 0 ⊕ 0 = 1 ∙ 0 ∙ 1 ∙ 1 = 0, por lo tanto, la salida de 𝐴3 = 𝐵3 es 0 “LOW", para las condición 𝐴2 = 𝐵2 𝑦 𝐴1 = 𝐵1, donde 𝐴2 = 1, 𝐴1 = 1, 𝐵1 = 1 𝑦 𝐵2 = 1, se obtiene una salida igual, es decir 𝐴2 = 𝐵2 𝑦 𝐴1 = 𝐵1 es 0 “LOW”, y para la condición 𝐴0 > 𝐵0, donde los valores de 𝐴0 = 1 y 𝐵0 = 0, su salida se puede verificar de la siguiente forma: ̅̅̅̅ + ̅̅̅̅̅̅̅̅̅̅̅̅ ̅̅̅̅ + ̅̅̅̅̅̅̅̅̅̅̅̅ ̅̅̅̅ + (𝐴 > 𝐵) = 𝐴3𝐵3 𝐴3 ⊕ 𝐵3 𝐴2𝐵2 𝐴3 ⊕ 𝐵3 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴2 ⊕ 𝐵2 𝐴1𝐵1 ̅̅̅̅̅̅̅̅̅̅̅̅ ̅̅̅̅ = 1 ∙ 1̅ + ̅̅̅̅̅̅̅̅ 𝐴3 ⊕ 𝐵3 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴2 ⊕ 𝐵2 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴1 ⊕ 𝐵1 𝐴0𝐵0 1 ⊕ 1 1 ∙ 0̅ + ̅̅̅̅̅̅̅̅ 1 ⊕ 1 ̅̅̅̅̅̅̅̅ 1 ⊕ 0 0 ̅̅̅ ∙0+ ̅̅̅̅̅̅̅̅ 1 ⊕ 1 ̅̅̅̅̅̅̅̅ 1 ⊕ 0 ̅̅̅̅̅̅̅̅ 0 ⊕ 0 0 ̅̅̅ ∙ 0 = 0 + 1 + 0 + 0 = 1, por lo tanto la salida 𝐴0 > 𝐵0 𝑒𝑠 1 "𝐻𝐼𝐺𝐻", esta salida se puede observar mediante la LED de color amarillo en la ilustración de la simulación. 𝐴3 = 𝐵3, 𝐴2 = 𝐵2, 𝐴1 = 𝐵1 𝑦 𝐴0 < 𝐵0 Se observo que para la condición 𝐴3 = 𝐵3, es decir 𝐴3 = 1 𝑦 𝐵3 = 1, su salida se puede verificar mediante la siguiente forma: (𝐴 = 𝐵) = ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴3 ⊕ 𝐵3 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴2 ⊕ 𝐵2 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴1 ⊕ 𝐵1 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴0 ⊕ 𝐵0 = ̅̅̅̅̅̅̅̅ 1 ⊕ 1 ̅̅̅̅̅̅̅̅ 1 ⊕ 0 ̅̅̅̅̅̅̅̅ 0 ⊕ 0 ̅̅̅̅̅̅̅̅ 0 ⊕ 0 = 1 ∙ 0 ∙ 1 ∙ 1 = 0, por lo tanto, la salida de 𝐴3 = 𝐵3 es 0 “LOW", para las condición 𝐴2 = 𝐵2 𝑦 𝐴1 = 𝐵1, donde 𝐴2 = 1, 𝐴1 = 1, 𝐵1 = 1 𝑦 𝐵2 = 1, se obtiene una salida igual, es decir 𝐴2 = 𝐵2 𝑦 𝐴1 = 𝐵1 es 0 “LOW”, y para la condición 𝐴0 < 𝐵0, donde los valores de 𝐴0 = 0 y 𝐵0 = 1, su salida se puede verificar de la siguiente forma: (𝐴 < 𝐵) = ̅̅̅̅̅ 𝐴3 ∙ 𝐵3 + ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴3 ⊕ 𝐵3 ̅̅̅̅̅ 𝐴2 ∙ 𝐵2 + ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴3 ⊕ 𝐵3 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴2 ⊕ 𝐵2 ̅̅̅̅̅ 𝐴1 ∙ 𝐵1 + ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴3 ⊕ 𝐵3 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴2 ⊕ 𝐵2 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴1 ⊕ 𝐵1 ̅̅̅̅ 𝐴0 ∙ 𝐵0 = ̅̅̅ 1 ∙ 1 + ̅̅̅̅̅̅̅̅ 1 ⊕ 1 ̅̅̅ 0 ∙ 1 + ̅̅̅̅̅̅̅̅ 1 ⊕ 1 ̅̅̅̅̅̅̅̅ 0 ⊕ 1 ̅̅̅ 0∙0+ ̅̅̅̅̅̅̅̅ 1 ⊕ 1 ̅̅̅̅̅̅̅̅ 0 ⊕ 1 ̅̅̅̅̅̅̅̅ 0 ⊕ 0 0̅ ∙ 0 = 0 + 1 + 0 + 0 = 1, por lo tanto la salida 𝐴0 < 𝐵0 𝑒𝑠 1 "𝐻𝐼𝐺𝐻", esta salida se puede observar mediante la LED de color verde en la ilustración de la simulación. 𝐴3 = 𝐵3, 𝐴2 = 𝐵2, 𝐴1 = 𝐵1 𝑦 𝐴0 = 𝐵0 Para las condiciones en donde todas tienen como entrada 1 lógico, en este caso se tuvo que emplear las entradas de expansión para las conexiones de entrada en cascada, en donde se ajustó la entrada 𝐴 = 𝐵 en 1 “HIGH”, este ajuste se requiere en condición de igualdad, por lo cual la salida 𝐴 = 𝐵, fue 1 “HIGH”, esto se puede verificar de la siguiente forma: (𝐴 = 𝐵) = ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴3 ⊕ 𝐵3 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴2 ⊕ 𝐵2 ̅̅̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴1 ⊕ 𝐵1 ̅̅̅̅̅̅̅̅̅̅̅̅ 𝐴0 ⊕ 𝐵0 = ̅̅̅̅̅̅̅̅ 1 ⊕ 1 ̅̅̅̅̅̅̅̅ 1 ⊕ 1 ̅̅̅̅̅̅̅̅ 1 ⊕ 1 ̅̅̅̅̅̅̅̅ 1⊕1=1∙1∙1∙1= 1 , por lo tanto la salida 𝐴 = 𝐵 es 1 “HIGH”, esta salida se puede observar mediante la LED de color rojo en la ilustración de la simulación. TABLA No. 1 A3,B3 A2,B2 A1,B1 A0,B0 A>B A<B A=B A3>B3 X X X 5V 0V 0V A3<B3 X X X 0V 5V 0V A3=B3 A2>B2 X X 5V 0V 0V A3=B3 A2<B2 X X 0V 5V 0V A3=B3 A2=B2 A1>B1 X 5V 0V 0V A3=B3 A2=B2 A1<B1 X 0V 5V 0V A3=B3 A2=B2 A1=B1 A0>B0 5V 0V 0V A3=B3 A2=B2 A1=B1 A0<B0 0V 5V 0V A3=B3 A2=B2 A1=B1 A0=B0 0V 0V 5V X: Don’t Care TABLA No. 1 (En niveles lógicos) A3,B3 A2,B2 A1,B1 A0,B0 A>B A<B A=B A3>B3 X X X 1 0 0 A3<B3 X X X 0 1 0 A3=B3 A2>B2 X X 1 0 0 A3=B3 A2<B2 X X 0 1 0 A3=B3 A2=B2 A1>B1 X 1 0 0 A3=B3 A2=B2 A1<B1 X 0 1 0 A3=B3 A2=B2 A1=B1 A0>B0 1 0 0 A3=B3 A2=B2 A1=B1 A0<B0 0 1 0 A3=B3 A2=B2 A1=B1 A0=B0 0 0 1 X: Don’t Care FIG. 3: Diagrama lógico del C.I 74LS85 CONCLUSIÓN Se logro el objetivo de implementar y describir el funcionamiento un comparador digital de magnitud utilizando las funciones lógicas AND, XOR y NOT, empleando bloques de circuitos integrados comerciales. Se comprobó las tablas de verdad de los circuitos de comparador de magnitud de dos bits y de cuatro bits. Se emplearon las entradas de expansión o en cascada para ajustar el modo de funcionamiento de las salidas del circuito, cuando las entradas se encuentran en igualdad. Los comparadores de magnitud son útiles en las aplicaciones de control en las que un número binario que representa la variable física que se está controlando (por ejemplo, posición, velocidad o temperatura) se compara con un valor de referencia. Las salidas del comparador se utilizan para operar circuitos que lleven la variable física hacia el valor de referencia. Tener cuidado al interconectar usando compuertas lógicas cuando se utiliza los C.I, ya que debe ser el modelo correcto y ser igual al de la hoja de datos del C.I seleccionado a utilizar, sino utilizar el modelo alternativo o emplear otro simulador. BIBLIOGRAFÍA Santiago Acha, M. A. (2002). Electrónica Digital introducción a la Lógica Digital. Teoría, Problemas y Simulación. (pag:134,136,308,467,468) TOCCI, R. J. (2007). Sistemas digitales principios y aplicaciones. México: Pearson. (pag:145-146, 621-623) FAIRCHILD SEMICONDUCTOR. (2000). DM74LS85 4-Bit Magnitude Comparator. (pag: 1-2)