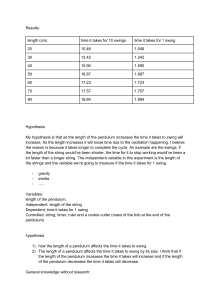
Contents 1 2 3 Introduction 1 1.1 Introduction 1 1.2 Preliminaries from Dynamics 4 1.3 Summary 19 Exercises 19 Modeling of Vibratory Systems 2.1 Introduction 23 2.2 Inertia Elements 24 2.3 Stiffness Elements 28 2.4 Dissipation Elements 49 2.5 Model Construction 54 2.6 Design for Vibration 60 2.7 Summary 61 Exercises 61 Single Degree-Of-Freedom Systems: Governing Equations 3.1 Introduction 69 3.2 Force-Balance and Moment-Balance Methods 70 23 69 1 Introduction 1.1 INTRODUCTION 1.2 PRELIMINARIES FROM DYNAMICS 1.2.1 Kinematics of Particles and Rigid Bodies 1.2.2 Generalized Coordinates and Degrees of Freedom 1.2.3 Particle and Rigid-Body Dynamics 1.2.4 Work and Energy 1.3 SUMMARY EXERCISES 1.1 INTRODUCTION Vibrations occur in many aspects of our life. For example, in the human body, there are low-frequency oscillations of the lungs and the heart, high-frequency oscillations of the ear, oscillations of the larynx as one speaks, and oscillations induced by rhythmical body motions such as walking, jumping, and dancing. Many man-made systems also experience or produce vibrations. For example, any unbalance in machines with rotating parts such as fans, ventilators, centrifugal separators, washing machines, lathes, centrifugal pumps, rotary presses, and turbines, can cause vibrations. For these machines, vibrations are generally undesirable. Buildings and structures can experience vibrations due to operating machinery; passing vehicular, air, and rail traffic; or natural phenomena such as earthquakes and winds. Pedestrian bridges and floors in buildings also experience vibrations due to human movement on them. In structural systems, the fluctuating stresses due to vibrations can result in fatigue failure. Vibrations are also undesirable when performing measurements with precision instruments such as an electron microscope and when fabricating microelectromechanical systems. In vehicle design, noise due to vibrating panels must be reduced. Vibrations, which can be responsible for unpleasant sounds called noise, are also responsible for the music that we hear. 1 2 CHAPTER 1 Introduction Vibrations are also beneficial for many purposes such as atomic clocks that are based on atomic vibrations, vibratory parts feeders, paint mixers, ultrasonic instrumentation used in eye and other types of surgeries, sirens and alarms for warnings, determination of fundamental properties of thin films from an understanding of atomic vibrations, and stimulation of bone growth. The word oscillations is often used synonymously with vibrations to describe to and fro motions; however, in this book, the word vibrations is used in the context of mechanical and biomechanical systems, where the system energy components are kinetic energy and potential energy. It is likely that the early interest in vibrations was due to development of musical instruments such as whistles and drums. As early as 4000 B.C., it is believed that in India and China there was an interest in understanding music, which is described as a pulsating effect due to rapid change in pitch. The origin of the harmonica can be traced back to 3000 B.C., when in China, a bamboo reed instrument called a “sheng” was introduced. From archeological studies of the royal tombs in Egypt, it is known that stringed instruments have also been around from about 3000 B.C. A first scientific study into such instruments is attributed to the Greek philosopher and mathematician Pythagoras (582–507 B.C.). He showed that if two like strings are subjected to equal tension, and if one is half the length of the other, the tones they produce are an octave (a factor of two) apart. It is interesting to note that although music is considered a highly subjective and personal art, it is closely governed by vibration principles such as those determined by Pythagoras and others who followed him. The vibrating string was also studied by Galileo Galilei (1564–1642), who was the first to show that pitch is related to the frequency of vibration. Galileo also laid the foundations for studies of vibrating systems through his observations made in 1583 regarding the motions of a lamp hanging from a cathedral in Pisa, Italy. He found that the period of motion was independent of the amplitude of the swing of the lamp. This property holds for all vibratory systems that can be described by linear models. The pendulum system studied by Galileo has been used as a paradigm to illustrate the principles of vibrations for many centuries. Galileo and many others who followed him have laid the foundations for vibrations, which is a discipline that is generally grouped under the umbrella of mechanics. A brief summary of some of the major contributors and their contributions is provided in Table 1.1. The biographies of many of the individuals listed in this table can be found in the Dictionary of Scientific Biography.1 It is interesting to note from Table 1.1 that the early interest of the investigators was in pendulum and string vibrations, followed by a phase where the focus was on membrane, plate, and shell vibrations, and a subsequent phase in which vibrations in practical problems and nonlinear oscillations received considerable attention. Lord Rayleigh’s book Theory of Sound, which was first published in 1877, is one of the early comprehensive publications on vibrations. In fact, 1 C. C. Gillispie, ed., Dictionary of Scientific Biography, 18 Vols., Scribner, New York (1970–1990). CHAPTER 1 Introduction 4 many of the mathematical developments that are commonly taught in a vibrations course can be traced back to the 1800s and before. However, since then, the use of these principles to understand and design systems has seen considerable growth in the diversity of systems that are designed with vibrations in mind: mechanical, electromechanical and microelectromechanical devices and systems, biomechanical and biomedical systems, ships and submarines, and civil structures. In this chapter, we shall show how to: • • • 1.2 Determine the displacement, velocity, and acceleration of a mass element. Determine the number of degrees of freedom. Determine the kinetic energy and the work of a system. PRELIMINARIES FROM DYNAMICS Dynamics can be thought as having two parts, one being kinematics and the other being kinetics. While kinematics deals with the mathematical description of motion, kinetics deals with the physical laws that govern a motion. Here, first, particle kinematics and rigid-body kinematics are reviewed. Then, the notions of generalized coordinates and degrees of freedom are discussed. Following that, particle dynamics and rigid-body dynamics are addressed and the principles of linear momentum and angular momentum are presented. Finally, work and energy are discussed. 1.2.1 Kinematics of Particles and Rigid Bodies Particle Kinematics In Figure 1.1, a particle in free space is shown. In order to study the motions of this particle, a reference frame R and a set of unit vectors2 i, j, and k fixed P Y r P/O j k (xp, yp, zp) O R X i Z FIGURE 1.1 Particle kinematics. R is reference frame in which the unit vectors i, j, and k are fixed. 2 As a convention throughout the book, bold and italicized letters represent vectors. 1.2 Preliminaries from Dynamics 5 in this reference frame are considered. These unit vectors, which are orthogonal with respect to each other, are assumed fixed in time; that is, they do not change direction and length with time t. A set of orthogonal coordinate axes pointing along the X, Y, and Z directions is also shown in Figure 1.1. The origin O of this coordinate system is fixed in the reference frame R for all time t. The position vector r P/O from the origin O to the particle P is written as rP/O x p i yp j zp k (1.1) where the superscript in the position vector is used to indicate that the vector runs from point O to point P. When there is no ambiguity about the position vector in question, as in Figure 1.1, this superscript notation is dropped for convenience; that is, r P/O ⬅ r. The particle’s velocity v and acceleration a, which are both vector quantities, are defined as, respectively, v dr dt a dv d 2r 2 dt dt (1.2) where the derivatives are with respect to time.3 Using Eqs. (1.1) and (1.2) and noting that the unit vectors do not change with time, one obtains d # v r 3 xp i yp j zp k4 dt d d d d d d 3 x 4 i xp 3 i4 3yp 4 j yp 3 j 4 3 zp 4 k zp 3 k4 dt p dt dt dt dt dt # # # xp i yp j zp k (1.3a) and d # # # # a v 3 xp i yp j zp k4 dt d # d # d # # d # d # d 3 xp 4i xp 3i 4 3 yp 4 j yp 3 j4 3 zp 4 3k4 zp 3 k4 dt dt dt dt dt dt $ $ $ xp i yp j zp k (1.3b) 3 The time-derivative operator d/dt is defined only when a reference frame is specified. To be precise, one would write Eqs. (1.2) as follows: R R P/O R P/O v dr P/O dt R 2 P/O dvP/O d r dt dt2 R a However, for notational ease, the superscripts have been dropped in this book. Throughout this book, although the presence of a reference frame such as R in Figure 1.1 is not made explicit, it is assumed that the time-derivative operator has been defined in a specific reference frame. 6 CHAPTER 1 Introduction where the over dot indicates differentiation with respect to time. Note that in arriving at Eqs. (1.3), the time derivatives of the unit vectors i, j, and k are all zero since these unit vectors are fixed (i.e., do not change with time) in the reference frame of interest. Planar Rigid-Body Kinematics A rigid body is shown in the X-Y plane in Figure 1.2 along with the coordinates of the center of mass of this body. In this figure, the unit vectors i, j, and k are fixed in reference frame R, while the unit vectors e1 and e2 are fixed in the reference frame R and they are defined such that the vector cross product e1 e2 k. While the unit vectors i, j, and k are fixed in time, the unit vectors e1 and e2 share the motion of the body and, therefore, change with respect to time. The velocity and acceleration of the center of mass of the rigid body with respect to the point O fixed in the reference frame R is determined in a manner similar to that previously discussed for the particle, and they are given by # # # vG/O r G/O xG i yG j $ $ $ aG/O r G/O x G i y G j (1.4) To determine the velocity and acceleration of any other point P on the body in terms of the corresponding quantities of the center of mass of the body, one needs to consider the angular velocity v and the angular acceleration a of the rigid body.4 Since the motion of the rigid body is confined to the plane in this case, both of these vectors point in the Z direction and they are each parallel to the unit vector k. In terms of the velocity and acceleration of e2 e1 Y R' G j k O (xG, yG, 0) R X i Z FIGURE 1.2 Planar rigid-body kinematics. 4 Again, for notational ease, instead of the precise notations of RvR and RaR for the angular velocity of the reference frame R with respect to R and the angular acceleration of the reference frame R with respect to R, respectively, the left and right superscripts have been dropped. 1.2 Preliminaries from Dynamics 7 the center of mass of the rigid body, the velocity and acceleration at any other point P on this body are written as vP/O vG/O v r P/G aP/O aG/O V v P/G A r P/G (1.5) where r P/G is the position vector from point G to point P, v P/O and a P/O are the velocity and acceleration of point P with respect to O, respectively, and again, the symbol “” refers to the vector cross product. Equations (1.5) are derived by starting from the definitions given by Eqs. (1.2). Noting from the first of Eqs. (1.5) that the relative velocity of point P with respect to G is given by vP/G vP/O vG/O V r P/G P/O the acceleration a (1.6) 5 is written as aP/O aG/O V 1V r P/G 2 A r P/G (1.7) Equations (1.5) through (1.7) hold for any two arbitrary points on the rigid body. If the body-fixed unit vectors e1 and e2 are used to resolve the position and velocity vectors when evaluating the velocities and accelerations using Eqs. (1.2), (1.5), (1.6), and (1.7), then one has to realize that the body-fixed unit vectors change orientation with respect to time; this is given by de1 V e1 dt de2 V e2 dt (1.8) In the definitions and relations provided in this section for velocities and accelerations, if the point O is fixed for all time in what is called an inertial reference frame,6 then the corresponding quantities are referred to as absolute velocities and absolute accelerations. These quantities are important for determining the governing equations of a system, as discussed in Section 1.2.3. Five examples are provided next to illustrate how particle and rigid-body kinematics can be used to describe the motion of rigid bodies that will be considered in the following chapters. 5 In arriving at Eqs. (1.7), it has been assumed that all of the time derivatives are being evaluated in reference frame R. 6 An inertial reference frame is an “absolute fixed” frame, which for our purposes does not share any of the motions of the particles or bodies considered in the vibration problems. (Of course, in a broader context, a true inertial reference frame does not exist.) Throughout this book, the reference frame R is used as an inertial reference frame, but it is not explicitly shown in Figure 1.3 and in any of the following figures in this chapter and later chapters. However, the choice of this frame is assumed in defining the absolute velocities and absolute accelerations. 8 CHAPTER 1 Introduction EXAMPLE 1.1 Kinematics of a planar pendulum Consider the planar pendulum shown in Figure 1.3, where the orthogonal unit vectors e1 and e2 are fixed to the pendulum and they share the motion of the pendulum. The unit vectors i, j, and k, which point along the X, Y and Z directions, respectively, are fixed in time. The velocity and acceleration of the planar pendulum P with respect to point O are the quantities of interest. The position vector from point O to point P is written as rP/O rQ/O rP/Q h j Le2 (a) Making use of Eqs. (1.2) and (1.8) and noting that# both h and L are constant with respect to time and the angular velocity v uk, the pendulum velocity is de2 LV e2 dt # # Luk e2 Lue1 vP/O L (b) and the pendulum acceleration is aP/O dv P/O dt # d1Lue1 2 $ # Lue1 LuV e1 dt $ # # Lue1 Lu 1uk e1 2 $ # Lue1 Lu 2e 2 (c) In arriving at Eqs. (b) and (c), the following relations have been used. k e2 e1 k e1 e2 FIGURE 1.3 (d) Y Planar pendulum. The reference frames are not explicitly shown in this figure, but it is assumed that the unit vectors i, j, and k are fixed in R and that the unit vectors e1 and e2 are fixed in R. Q L e2 j h e1 P k O X i Z (xp, yp, 0) 1.2 Preliminaries from Dynamics 9 Noting that the unit vectors e1 and e2, which are fixed to the pendulum, are resolved in terms of the unit vectors i and j as follows, e1 cos ui sin u j e2 sin ui cos u j (e) one can rewrite the velocity and acceleration of the pendulum given by Eqs. (b) and (c), respectively, as # vP/O Lu 1cos ui sin u j 2 $ # $ # aP/O 1Lu cos u Lu 2 sin u 2 i 1Lu sin u Lu 2 cos u 2 j (f) EXAMPLE 1.2 Kinematics of a rolling disc A disc of radius r rolls without slipping in the X-Y plane, as shown in Figure 1.4. We shall determine the velocity and acceleration of the center of mass with# respect to the point O. The unit vectors e1 and e2 are fixed to the disc and u is the angular speed of the disc. To determine the velocity of the center of mass of the disc located at G with respect to point O, the first of Eqs. (1.5) is used; that is, vG/O vC/O V rG/C (a) Noting that the instantaneous velocity of the point of contact vC/O is zero, # the angular velocity V uk, and rG/C rj, the velocity of point G with respect to the origin O can be evaluated. In addition, from the definitions given by Eqs. (1.2), the acceleration can be evaluated. The resulting expressions are # # vG/O uk rj rui $ aG/O ru i (b) As expected, the center of mass of a disc rolling along a straight line does not experience any vertical acceleration due to this motion. e2 . Y G e1 r j C k O X i Z FIGURE 1.4 Rolling disc. 10 CHAPTER 1 Introduction EXAMPLE 1.3 Kinematics of a particle in a rotating frame7 A particle is free to move in a plane, which rotates about an axis normal to the plane as shown in Figure 1.5. The unit vectors i and j, which point along the X and Y directions, respectively, have fixed directions for all time. We shall be determining the velocity of the particle P located in the x-y plane. The x-y-z frame rotates with respect to the X-Y-Z frame, which is fixed in time. The rotation takes place about the z-axis with an angular speed v. The unit vector k is oriented along the axis of rotation, which points along the z direction. The unit vectors e1 and e2 are fixed to the rotating frame, and they point along the x and y directions, respectively. In the rotating frame, the position vector from the fixed point O to the point P is r xpe1 ype2 (a) Making use of the first of Eqs. (1.2) for the velocity of a particle, noting Eqs. (1.8), recognizing that V vk, and making use of Eqs. (d) of Example 1.1, the velocity of the particle is v d d dr 1xpe1 2 1ype2 2 dt dt dt de1 de2 # # xpe1 xp ype2 yp dt dt # # 1xp vyp 2 e1 1yp vx p 2 e2 (b) y Y P (xp, yp, 0) e2 j X k i Z O k x e1 z FIGURE 1.5 Particle in a rotating frame. 7 In Chapters 7 and 8, the particle kinematics discussed here will be used in examining vibrations of a gyro-sensor. 1.2 Preliminaries from Dynamics EXAMPLE 1.4 11 Absolute velocity of a pendulum attached to a rotating disc We shall determine the absolute velocity of the pendulum attached to the rotating disc shown in Figure 1.6. This system is representative of a centrifugal pendulum absorber treated in Chapter 8. Assume that the point O is fixed in an inertial reference frame, the unit vectors e1 and e2 are fixed to the pendulum, and that the orthogonal unit vectors e¿1 and e¿2 are fixed to the rotating disc. The motions of the pendulum are restricted to the plane containing the unit vectors e1 and e2, the angle u describes the rotation of the disc with respect to the horizontal, and the angle w describes the position of the pendulum relative to the disc. From the figure, we see that the position vector describing the location of the mass m is rm Re¿1 re1 1R r cosw2 e¿1 r sinwe¿2 Re¿1 r coswe¿1 r sinwe¿2 Then, the velocity of mass m is Vm drm de¿1 de¿2 d d e¿1 1R r cosw 2 1R r cosw 2 e¿2 1r sinw 2 r sinw dt dt dt dt dt e1 e2 m e1' r e2' Pivot O' O R JO FIGURE 1.6 Pendulum attached to a rotating disc. 12 CHAPTER 1 Introduction Since the orientation of the unit vectors e¿1 and e¿2 change with time due to the rotation of the disc, we have # # de¿1 V e¿1 uk e¿1 ue¿2 dt # # de¿2 V e¿2 uk e¿2 ue¿1 dt # # # # Vm rw sin we¿1 1R r cos w 2 ue¿2 rw cos we¿2 ru sin we¿1 # # # # # r 1w u 2 sin we¿1 1Ru r1w u 2 cos w2 e¿2 which leads to EXAMPLE 1.5 Moving mass on a rotating table8 Consider a mass m that is held by elastic constraints and is located on a table that is rotating at a constant speed v, as shown in Figure 1.7. We shall determine the absolute velocity of the mass. We assume that point O is fixed in the vertical plane, that the unit vectors e1 and e2 are fixed to the mass m, as shown in Figure 1.7, and that k e1 e2. Then rm re1 and the velocity is given by e1 m e2 r L O FIGURE 1.7 Frictionless rotating table of radius L on which mass m is elastically constrained. 8 N. S. Clarke, “The Effect of Rotation upon the Natural Frequencies of a Mass-Spring System,” J. Sound Vibration, 250(5), pp. 849–887 (2000). Vm drm d 3 re1 4 dt dt de1 # re1 r dt # re1 r1v # re1 r1v 1.2 Preliminaries from Dynamics 13 # u 2 k e1 # u 2 e2 1.2.2 Generalized Coordinates and Degrees of Freedom To describe the physical motion of a system, one needs to choose a set of variables or coordinates, which are referred to as generalized coordinates.9 They are commonly represented by the symbol qk. The motion of a free particle, which is shown in Figure 1.8a, is described by using the generalized coordinates q1 xp, q2 yp, and q3 zp. Here, all three of these coordinates are needed to describe the motion of the system. The minimum number of independent coordinates needed to describe the motion of a system is called the degrees of freedom of a system. Any free particle in space has three degrees of freedom. In Figure 1.8b, a planar pendulum is shown. The pivot point of this pendulum is fixed at (xt,yt,0) and the pendulum has a constant length L. For this case, the coordinates are chosen as xp and yp. However, since the pendulum length is constant, these coordinates are not independent of each other because 1xp xt 2 2 1yp yt 2 2 L2 (1.9) Equation (1.9) is an example of a constraint equation, which in this case is a geometric constraint.10 The motion of the pendulum in the plane can be described by using either xp or yp. Since xp L sin u and yp L L cos u, one can also use the variable u to describe the motion of the pendulum, which is an independent coordinate that qualifies as a generalized coordinate. Since only one independent variable or coordinate is needed to describe the pendulum’s motion, a planar pendulum of constant length has one degree of freedom. As a third example, a dumbbell in the plane is considered in Figure 1.8c. In this system of particles, a massless rod of constant length connects two particles. Here, the coordinates are chosen as xa, ya, xb, and yb, where this 9 In a broader context, the term “generalized coordinates” is also used to refer to any set of parameters that can be used to specify the system configuration. There are subtle distinctions in the definitions of generalized coordinates used in the literature. Here, we refer to the generalized coordinates as the coordinates that form the minimum set or the smallest possible number of variables needed to describe a system (J. L. Synge and B. A. Griffith, Principles of Mechanics, Section 10.6, McGraw Hill, New York, 1959). 10 A geometric constraint is an example of a holonomic constraint, which can be expressed in the form f(q1, q2, . . . , qn; t ) 0, where qi are the generalized coordinates and t is time. 14 CHAPTER 1 Introduction Y Y P (xt, yt, 0) L (xp, yp, zp) (xt xp)2 (yt yp) O Z (xp, yp, 0) O X X Z (a) (b) (xb, yb, 0) Y Y (xG, yG, 0) (xa, ya, 0) O X Z O X Z (c) (d) FIGURE 1.8 (a) Free particle in space; (b) planar pendulum; (c) dumbbell in plane; and (d) free rigid body in plane. set includes the coordinates of each of the two particles in the plane. Since the length of the dumbbell is constant, only three of these coordinates are independent. A minimum of three of the four coordinates is needed to describe the motion of the dumbbell in the plane. Hence, a dumbbell in the plane has three degrees of freedom. The generalized coordinates in this case are chosen as xG, yG, and u, where xG and yG are the coordinates of the center of mass of the dumbbell and u represents the rotation about an axis normal to the plane of the dumbbell. In Figure 1.8d, a rigid body that is free to move in the X–Y plane is shown. The generalized coordinates q1 xG and q2 yG specify the translation of the center of mass of the rigid body. Apart from these two generalized coordinates, another generalized coordinate u, which represents the rotation about the Z-axis, is also needed. Hence, a rigid body that is free to move in the plane has three degrees of freedom. It is not surprising that the dumbbell in the plane has the same number of degrees of freedom as the rigid body shown in Figure 1.8d, since the collection of two particles, which are a fixed distance L apart in Figure 1.8c, is a rigid body. In the examples shown in Figures 1.8b and 1.8c, one needed to take into account the constraint equations in determining the number of degrees of freedom of a system. For a system configuration specified by n coordinates, 1.2 Preliminaries from Dynamics 15 which are related by m independent constraints, the number of degrees of freedom N is given by Nnm (1.10) The dynamics of vibratory systems with a single degree of freedom is treated in Chapters 3 through 6, the dynamics of vibratory systems with finite but more than one degree of freedom is treated in Chapters 7 and 8, and the dynamics of vibratory systems with infinite number of degrees of freedom is treated in Chapter 9. For much of the material presented in these chapters, the physical systems move in the plane and the systems are subjected only to geometric constraints. 1.2.3 Particle and Rigid-Body Dynamics In the previous two subsections, it was shown how one can determine the velocities and accelerations of particles and rigid bodies and the number of independent coordinates needed to describe the motion of a system. Here, a discussion of the physical laws governing the motion of a system is presented. The velocities and accelerations determined from kinematics will be used in applying these laws to a system. For all systems treated in this book, the speeds at which the systems travel will be much less than the speed of light. In the area of mechanics, the dynamics of such systems are treated under the area broadly referred to as Newtonian Mechanics. Two important principles that are used in this area are the principle of linear momentum and the principle of angular momentum, which are due to Newton and Euler, respectively. Principle of Linear Momentum The Newtonian principle of linear momentum states that in an inertial reference frame, the rate of change of the linear momentum of a system is equal to the total force acting on this system. This principle is stated as F dp dt (1.11) where F represents the total force vector acting on the system and p represents the total linear momentum of the system. Again, it is important to note that the time derivative in Eq. (1.11) is defined in an inertial reference frame and that the linear momentum is constructed based on the absolute velocity of the system of interest. Particle Dynamics For a particle, the linear momentum is given by p mv (1.12) where m is the mass of the particle and v is the absolute velocity of the particle. When the mass m is constant, Eq. (1.11) takes the familiar form CHAPTER 1 Introduction 16 xi Y F Fi m j k O X i Z FIGURE 1.9 Free particle of mass m translating along the i direction. d1mv 2 dt ma (1.13) which is referred to as Newton’s second law of motion. The velocity in Eq. (1.12) and the acceleration in Eq. (1.13) are determined from kinematics. Therefore, for the particle shown in Figure 1.9, it follows from Eq. (1.13) that $ Fi mx i or $ F mx Dynamics of a System of n Particles For a system of n particles, the principle of linear momentum is written as n n dpi dp F a Fi a dt i1 i1 dt n dvi a mi dt i1 (1.14) where the subscript i refers to the ith particle in the collection of n particles, Fi is the external force acting on particle i, pi is the linear momentum of this particle, mi is the constant mass of the ith particle, and vi is the absolute velocity of the ith particle. For the jth particle in this collection, the governing equation takes the form n dvj dpj Fj a Fij mj dt dt i1 (1.15) ij where Fij is the internal force acting on particle j due to particle i. Note that in going from the equation of motion for an individual particle given by Eq. (1.15) to that for a system of particles given by Eq. (1.14), it is assumed that all of the internal forces satisfy Newton’s third law of motion; that is, the assumption of equal and opposite internal forces 1Fij Fji 2 . If the center of mass of the system of particles is located at point G, then Eq. (1.14) can be shown to be equivalent to F d1mvG 2 dt (1.16) where m is the total mass of the system and vG is the absolute velocity of the center of mass of the system. Equation (1.16) is also valid for a rigid body. It is clear from Eq. (1.11) that in the absence of external forces, the linear momentum of the system is conserved; that is, the linear momentum of the system is constant for all time. This is an important conservation theorem, which is used, when applicable, to examine the results obtained from analysis of vibratory models. 1.2 Preliminaries from Dynamics 17 Principle of Angular Momentum The principle of angular momentum states that the rate of change of the angular momentum of a system with respect to the center of mass of the system or a fixed point is equal to the total moment about this point. This principle is stated as M dH dt (1.17) where the time derivative is evaluated in an inertial reference frame, M is the net moment acting about a fixed point O in an inertial reference frame or about the center of mass G, and H is the total angular momentum of the system about this point. For a particle, the angular momentum is given by Hrp (1.18) where r is the position vector from the fixed point O to the particle and p is the linear momentum of this particle based on the absolute velocity of this particle. For a system of n particles, the principle given by Eq. (1.17) can be applied with respect to either the center of mass G of the system or a fixed point O. The angular momentum takes the form n n H a Hi a ri pi i1 (1.19) i1 where ri is the position vector from either point O or point G to the ith particle and pi is the linear momentum of the particle based on the absolute velocity of the particle. For a rigid body moving in the plane as in Figure 1.8d, the angular momentum about the center of mass is given by # (1.20) HG JG uk where JG is the mass moment of inertia about the center of mass and the unit vector k points along the Z-direction. The angular momentum of the rigid body about the fixed point O is given by # (1.21) HO JO uk where JO is the mass moment of inertia about the fixed point. From Eq. (1.17), it is clear that in the absence of external moments, the angular momentum of the system is conserved; that is, the angular momentum of the system is constant for all time. This is another important conservation theorem, which is used, when applicable, to examine the results obtained from analysis of vibratory models. The governing equations derived for vibratory systems in the subsequent chapters are based on Eqs. (1.11) and (1.17). Specific examples are not provided here, but the material provided in later chapters are illustrative of how these important principles are used for developing mathematical models of a system. 18 CHAPTER 1 Introduction 1.2.4 Work and Energy The definition for kinetic energy T of a system is provided and the relation between work done on a system and kinetic energy is presented. The kinetic energy of a system is a scalar quantity. For a system of n particles, the kinetic energy is defined as T 1 n 1 n # ## m 1r r 2 mi 1vi # vi 2 i i i 2 ia 2 ia 1 1 (1.22) where vi is the absolute velocity of the ith particle and the “ⴢ” symbol is the scalar dot product of two vectors. For a rigid body, the kinetic energy is written in the following convenient form, which is due to König,11 T T1translational2 T1rotational2 (1.23) 1 # 1 m 1vG # vG 2 JG u2 2 2 (1.24) 1 #2 JOu 2 (1.25) where the first term on the right-hand side represents the kinetic energy associated with the translation of the system and the second term on the right-hand side represents the kinetic energy associated with rotation about the center of mass of the system. For a rigid body moving in the plane as shown in Figure 1.8d, the kinetic energy takes the form T where the first term on the right-hand side is the translational part based on the velocity vG of the center of mass of the system and the second term on the right-hand side is associated with rotation about an axis, which passes through the center of mass and is normal to the plane of motion. For a rigid body rotating in the plane about a fixed point O, the kinetic energy is determined from T Work-Energy Theorem According to the work-energy theorem, the work done in moving a system from a point A to point B is equal to the change in kinetic energy of the system, which is stated as WAB TB TA (1.26) where WAB is the work done in moving the system from the initial point A to the final point B, TB is the kinetic energy of the system at point B, and TA is the kinetic energy of the system at point A. The work done WAB is a scalar quantity. 11 D. T. Greenwood, Principles of Dynamics, Prentice Hall, Upper Saddle River, NJ, Chapter 4 (1988). Exercises 19 Another form of energy called potential energy of a system is addressed in Chapter 2. Specific examples are not provided here, but the use of kinetic energy and work done in developing mathematical models of vibratory systems is illustrated in the subsequent chapters. 1.3 SUMMARY In this chapter, a review from dynamics has been presented in the spirit of summarizing material that is typically a prerequisite to the study of vibrations. In carrying out this discussion, attention has been paid to kinematics, the notion of degree of freedom, and the principles of linear and angular momentum. This background material provides a summary of the foundation for the material presented in the subsequent chapters. EXERCISES Section 1.1 1.1 Choose any two contributors from Table 1.1, study their contributions, and write a paragraph about each of them. r1 Section 1.2.1 Slider of mass Mr 1.2 Consider the planar pendulum kinematics dis- cussed in Example 1.1, start with position vector r P/O resolved in terms the unit vectors i and j, and verify the expressions obtained for the acceleration and velocity given by Eq. (f) of Example 1.1. (t) Bar of rotary inertia JO O 1.3 Consider the kinematics of the rolling disc considered in Example 1.2, and verify that the instantaneous acceleration of the point of contact is not zero. 1.4 Show that the acceleration of the particle in the rotating frame of Example 1.3 is $ # a 1xp 2vyp v2xp ayp 2 e1 # $ 1yp 2vxp v2yp axp 2 e2 where a is the magnitude of the angular acceleration of the rotating frame about the z axis. 1.5 In Figure E1.5, a slider of mass Mr is located on a bar whose angular displacement in the plane is described by the coordinate u. The motion of the slider from FIGURE E1.5 the pivot point is measured by the coordinate r1. The acceleration due to gravity acts in a direction normal to the plane of motion. Assume that the point O is fixed in an inertial reference frame and determine the absolute velocity and absolute acceleration of the slider. 1.6 Consider the pendulum of mass m attached to a moving pivot shown in Figure E1.6. Assume that the pivot point cannot translate in the vertical direction. If the horizontal translation of the pivot point from the fixed point O is measured by the coordinate x and the