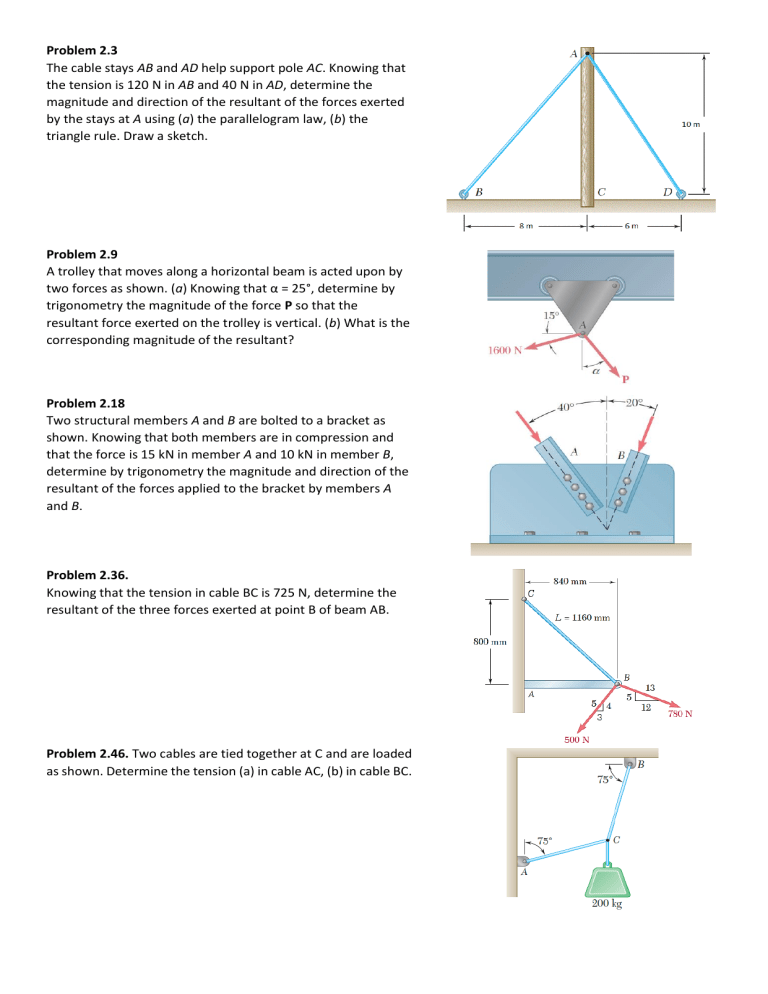
Problem 2.3 The cable stays AB and AD help support pole AC. Knowing that the tension is 120 N in AB and 40 N in AD, determine the magnitude and direction of the resultant of the forces exerted by the stays at A using (a) the parallelogram law, (b) the triangle rule. Draw a sketch. Problem 2.9 A trolley that moves along a horizontal beam is acted upon by two forces as shown. (a) Knowing that α = 25°, determine by trigonometry the magnitude of the force P so that the resultant force exerted on the trolley is vertical. (b) What is the corresponding magnitude of the resultant? Problem 2.18 Two structural members A and B are bolted to a bracket as shown. Knowing that both members are in compression and that the force is 15 kN in member A and 10 kN in member B, determine by trigonometry the magnitude and direction of the resultant of the forces applied to the bracket by members A and B. Problem 2.36. Knowing that the tension in cable BC is 725 N, determine the resultant of the three forces exerted at point B of beam AB. Problem 2.46. Two cables are tied together at C and are loaded as shown. Determine the tension (a) in cable AC, (b) in cable BC. Problem 2.51 A welded connection is in equilibrium under the action of the four forces shown. Knowing that FA = 8 kN and FB = 16 kN, determine the magnitudes of the other two forces. Problem 2.81 A force acts at the origin of a coordinate system in a direction defined by the angles θx = 70.9° and θy = 144.9°. Knowing that the z component of the force is -52 N, determine (a) the angle θz, (b) the other components and the magnitude of the force. Problem 2.82 A force acts at the origin of a coordinate system in a direction defined by the angles θy = 55° and θz = 45°. Knowing that the x component of the force is -500 N, determine (a) the angle θx, (b) the other components and the magnitude of the force. Problem 2.83 A force F of magnitude 210 N acts at the origin of a coordinate system. Knowing that Fx = 80 N, θz = 151.2°, and Fy < 0, determine (a) the components Fy and Fz, (b) the angles θx and θy. Problem 2.87 A frame ABC is supported in part by cable DBE that passes through a frictionless ring at B. Knowing that the tension in the cable is 385 N, determine the components of the force exerted by the cable on the support at D. Problem 2.107 Three cables are connected at A, where the forces P and Q are applied as shown. Knowing that Q = 0, find the value of P for which the tension in cable AD is 305 N. Problem 2.108 Three cables are connected at A, where the forces P and Q are applied as shown. Knowing that P = 1200 N, determine the values of Q for which cable AD is taut. Problem 3.5 An 8 N force P is applied to a shift lever. Determine the moment of P about B when α is equal to 25°. Problem 3.6 For the shift lever shown (right), determine the magnitude and the direction of the smallest force P that has a 210 Nm clockwise moment about B. Problem 3.7 An 11 N force P is applied to a shift lever. The moment of P about B is clockwise and has a magnitude of 250 Nm Determine the value of α. 220 mm 80 mm Problem 3.19 Determine the moment about the origin O of the force F = 4i + 5j - 3k (Newtons) that acts at a point A. Assume that the position vector of A is ( a) r = 2i - 3j + 4k, ( b) r = 2i + 2.5j - 1.5 k, (c) r = 2i + 5j + 6k. Problem 3.21 A 200-N force is applied as shown to the bracket ABC . Determine the moment of the force about A. Problem 3.41 Knowing that the tension in cable AC is 1260 N, determine ( a ) the angle between cable AC and the boom AB, ( b ) the projection on AB of the force exerted by cable AC at point A . Problem 3.46 Given the vectors P = 4i - 2j + 3k , Q = 2i + 4j - 5k , and S = Sxi - j + 2k, determine the value of Sx for which the three vectors are coplanar. Problem 3.50 To lift a heavy crate, a man uses a block and tackle attached to the bottom of an I-beam at hook B . Knowing that the man applies a 195-N force to end A of the rope and that the moment of that force about the y axis is 132 Nm, determine the distance a . Problem 3.111 Four forces act on a 700 3 375-mm plate as shown. ( a ) Find the resultant of these forces. ( b ) Locate the two points where the line of action of the resultant intersects the edge of the plate. Problem 3.112 Solve Prob. 3.111, assuming that the 760-N force is directed to the right. Problem 3.147 A crate of mass 80 kg is held in the position shown. Determine ( a ) the moment produced by the weight W of the crate about E , ( b ) the smallest force applied at B that creates a moment of equal magnitude and opposite sense about E . Problem 3.157 A blade held in a brace is used to tighten a screw at A. ( a ) Determine the forces exerted at B and C , knowing that these forces are equivalent to a force-couple system at A consisting of R = - (30 N)i + Ryj+Rzk and MRA = - (12 Nm)i . ( b ) Find the corresponding values of R y and R z . ( c ) What is the orientation of the slot in the head of the screw for which the blade is least likely to slip when the brace is in the position shown? Problem 4.2 A gardener uses a 60-N wheelbarrow to transport a 250-N bag of fertilizer. What force must she exert on each handle? Problem 4.3 The gardener wishes to transport a second 250-N bag of fertilizer at the same time as the first one. Determine the maximum allowable horizontal distance from the axle A of the wheelbarrow to the center of gravity of the second bag if she can hold only 75 N with each arm. Problem 4.9 The maximum allowable value of each of the reactions is 180 N. Neglecting the weight of the beam, determine the range of the distance d for which the beam is safe. Problem 4.92 Two tape spools are attached to an axle supported by bearings at A and D. The radius of spool B is 30 mm and the radius of spool C is 40 mm. Knowing that TB = 80 N and that the system rotates at a constant rate, determine the reactions at A and D. Assume that the bearing at A does not exert any axial thrust and neglect the weights of the spools and axle. Problem 4.95 A 200-mm lever and a 240-mm-diameter pulley are welded to the axle BE that is supported by bearings at C and D. If a 720-N vertical load is applied at A when the lever is horizontal, determine (a) the tension in the cord, (b) the reactions at C and D. Assume that the bearing at D does not exert any axial thrust. 4.142 A hand truck is used to move two kegs, each of mass 40 kg. Neglecting the mass of the hand truck, determine (a) the vertical force P that should be applied to the handle to maintain equilibrium when α = 35°, (b) the corresponding reaction at each of the two wheels. Problem 5.1 Problem 5.2 Problem 5.5 Problems 5.68 and 5.73 Determine the reactions at the beam supports for the given loading. Problem 5.100 For the stop bracket shown, locate the x coordinate of the center of gravity. Problem 5.103 For the machine element shown, locate the y coordinate of the center of gravity. Problem 5.115 Locate the center of gravity of the figure shown, knowing that it is made of thin brass rods of uniform diameter. Problem 6.165 Using the method of joints, determine the force in each member of the double-pitch roof truss shown. State whether each member is in tension or compression. Problem 6.129 A couple M of magnitude 1.5 kNm is applied to the crank of the engine system shown. For each of the two positions shown below, determine the force P required to hold the system in equilibrium. 6.130 A force P of magnitude 16 kN is applied to the piston of the engine system shown. For each of the two positions shown, determine the couple M required to hold the system in equilibrium. Problem 7.5 Determine the internal forces at point J of the structure shown. Problem 7.36 For the beam and loading shown, (a) draw the shear and bending-moment diagrams, (b) determine the maximum absolute values of the shear and bending moment. Problem 7.78 For the beam and loading shown, (a) draw the shear and bending-moment diagrams, (b) determine the magnitude and location of the maximum bending moment. Problem 8.9 The coefficients of friction between the block and the rail are μs = 0.30 and μk = 0.25. Knowing that θ = 65°, determine the smallest value of F required (a) to start the block moving up the rail, (b) to keep it from moving down. Problems 8.11 and 8.12 The coefficients of friction are μs = 0.40 and μk = 0.30 between all surfaces of contact. Determine the smallest force P required to start the 30-kg block moving if cable AB (a) is attached as shown, (b) is removed. Problem 8.21. A 6.5-m ladder AB leans against a wall as shown. Assuming that the coefficient of static friction μs is zero at B, determine the smallest value of μs at A for which equilibrium is maintained. Problem 8.22. A 6 .5-m ladder AB leans against a wall as shown. Assuming that the coefficient of static friction μs is the same at A and B, determine the smallest value of μs for which equilibrium is maintained. Problem 8.51 The elevation of the end of the steel beam supported by a concrete floor is adjusted by means of the steel wedges E and F. The base plate CD has been welded to the lower flange of the beam, and the end reaction of the beam is known to be 100 kN. The coefficient of static friction is μs = 0.30 between two steel surfaces and μs = 0.60 between steel and concrete. If the horizontal motion of the beam is prevented by the force Q, determine (a) the force P required to raise the beam, (b) the corresponding force Q. Problem 8.53 Block A supports a pipe column and rests as shown on wedge B. Knowing that the coefficient of static friction μs at all surfaces of contact is 0.25 and that θ = 45°, determine the smallest force P required to raise block A. Problem 8.112 A band brake is used to control the speed of a flywheel as shown. The coefficients of friction are μs = 0.30 and μk = 0.25. Determine the magnitude of the couple being applied to the flywheel, knowing that P = 45 N and that the flywheel is rotating counterclockwise at a constant speed. Problem 8.134 A worker slowly moves a 50-kg crate to the left along a loading dock by applying a force P at corner B as shown. Knowing that the crate starts to tip about the edge E of the loading dock when a 5 200 mm, determine (a) the coefficient of kinetic friction between the crate and the loading dock, (b) the corresponding magnitude P of the force. Problem 9.22 Determine the polar moment of inertia and the polar radius of gyration of the shaded area shown with respect to point P. Problem 9.31 Determine the moment of inertia and the radius of gyration of the shaded area with respect to the x axis. Problem 9.71 Using the parallel-axis theorem, determine the product of inertia of the area shown with respect to the centroidal x and y axes. Problem 9.141 The machine element shown is fabricated from steel. Determine the mass moment of inertia of the assembly with respect to (a) the x axis, (b) the y axis, (c) the z axis. (The density of steel is 7850 kg/m3.) Problem 9.153 A section of sheet steel 2 mm thick is cut and bent into the machine component shown. Knowing that the density of steel is 7850 kg/m3, determine the mass products of inertia Ixy, Iyz, and Izx of the component. Problem 10.82 A spring AB of constant k is attached to two identical gears as shown. Knowing that the spring is undeformed when θ = 0, and given that a = 60 mm, b = 45 mm, r = 90 mm, and k = 6 kN/m, determine (a) the range of values of P for which a position of equilibrium exists, (b) two values of 8 corresponding to equilibrium if the value of P is equal to half the upper limit of the range found in part a. Problem 11.1 The motion of a particle is defined by the relation x = 1.5t4 - 30t2 + 5t + 10, where x and t are expressed in meters and seconds, respectively. Determine the position, the velocity, and the acceleration of the particle when t = 4 s. Problem 11.2 The motion of a particle is defined by the relation x = 12t3 - 18t2 + 2t + 5, where x and t are expressed in meters and seconds, respectively. Determine the position and the velocity when the acceleration of the particle is equal to zero. Problem 11.3 The motion of a particle is defined by the relation x = 5/3 t3 – 5/2 t2 - 30t + 8x, where x and t are expressed in meters and seconds, respectively. Determine the time, the position, and the acceleration when v = 0. Problem 11.4 The motion of a particle is defined by the relation x = 6t2 - 8 + 40 cos πt, where x and t are expressed in meters and seconds, respectively. Determine the position, the velocity, and the acceleration when t = 6 s. Problem 11.5 The motion of a particle is defined by the relation x = 6t4 - 2t3 - 12t2 + 3t + 3, where x and t are expressed in meters and seconds, respectively. Determine the time, the position, and the velocity when a = 0. Problem 11.6 The motion of a particle is defined by the relation x = 2t3 - 15t2 + 24t + 4, where x is expressed in meters and t in seconds. Determine (a) when the velocity is zero, (b) the position and the total distance travelled when the acceleration is zero. Problem 11.7 The motion of a particle is defined by the relation x = t3 - 6t2 - 36t - 40, where x and t are expressed in meters and seconds, respectively. Determine (a) when the velocity is zero, (b) the velocity, the acceleration, and the total distance travelled when x = 0. Problem 11.8 The motion of a particle is defined by the relation x = t3 - 9t2 + 24t - 8, where x and t are expressed in meters and seconds, respectively. Determine (a) when the velocity is zero, (b) the position and the total distance travelled when the acceleration is zero. Problem 11.9 The acceleration of a particle is defined by the relation a = 28 m/s2. Knowing that x = 20 m when t = 4 s and that x = 4 m when v = 16 m/s, determine (a) the time when the velocity is zero, (b) the velocity and the total distance travelled when t = 11 s. Problem 11.10 The acceleration of a particle is directly proportional to the square of the time t. When t = 0, the particle is at x = 24 m. Knowing that at t = 6 s, x = 96 m and v = 18 m/s, express x and v in terms of t. Problem 11.33 A motorist enters a freeway at 45 km/h and accelerates uniformly to 99 km/h. From the odometer in the car, the motorist knows that she travelled 0.2 km while accelerating. Determine (a) the acceleration of the car, (b) the time required to reach 99 km/h. Problem 11.40 As relay runner A enters the 20-m-long exchange zone with a speed of 12.9 m/s, he begins to slow down. He hands the baton to runner B 1.82 s later as they leave the exchange zone with the same velocity. Determine (a) the uniform acceleration of each of the runners, (b) when runner B should begin to run. Problem 11.44 Two automobiles A and B are approaching each other in adjacent highway lanes. At t 5 0, A and B are 1 km apart, their speeds are vA = 108 km/h and vB = 63 km/h, and they are at points P and Q, respectively. Knowing that A passes point Q 40 s after B was there and that B passes point P 42 s after A was there, determine (a) the uniform accelerations of A and B, (b) when the vehicles pass each other, (c) the speed of B at that time. Problem 11.69 Two road rally checkpoints A and B are located on the same highway and are 12 km apart. The speed limits for the first 8 km and the last 4 km of the section of highway are 100 km/h and 70 km/h, respectively. Drivers must stop at each checkpoint, and the specified time between points A and B is 8 min 20 s. Knowing that a driver accelerates and decelerates at the same constant rate, determine the magnitude of her acceleration if she travels at the speed limit as much as possible. Problem 11.89 The motion of a particle is defined by the equations x = 4t3 - 5t2 + 5t and y = 5t2 - 15t, where x and y are expressed in millimetres and t is expressed in seconds. Determine the velocity and the acceleration when (a) t = 1 s, (b) t = 2 s. Problem 11.91 The motion of a particle is defined by the equations x = t2 - 8t + 7 and y = 0.5t2 + 2t - 4, where x and y are expressed in meters and t in seconds. Determine (a) the magnitude of the smallest velocity reached by the particle, (b) the corresponding time, position, and direction of the velocity. Problem 11.101 A volleyball player serves the ball with an initial velocity v0 of magnitude 13.40 m/s at an angle of 20° with the horizontal. Determine (a) if the ball will clear the top of the net, (b) how far from the net the ball will land. Problem 11.138 A monorail train starts from rest on a curve of radius 400 m and accelerates at the constant rate at. If the maximum total acceleration of the train must not exceed 1.5 m/s2, determine (a) the shortest distance in which the train can reach a speed of 72 km/h, (b) the corresponding constant rate of acceleration at. Problem 12.6 Determine the maximum theoretical speed that an automobile starting from rest can reach after traveling 400 m. Assume that the coefficient of static friction is 0.80 between the tires and the pavement and that (a) the automobile has front-wheel drive and the front wheels support 62 percent of the automobile’s weight, (b) the automobile has rear-wheel drive and the rear wheels support 43 percent of the automobile’s weight. Problem 12.9 A 20-kg package is at rest on an incline when a force P is applied to it. Determine the magnitude of P if 10 s is required for the package to travel 5 m up the incline. The static and kinetic coefficients of friction between the package and the incline are both equal to 0.3. Problem 12.71 The 100-g pin B slides along the slot in the rotating arm OC and along the slot DE which is cut in a fixed horizontal plate. Neglecting friction and knowing that rod OC rotates at the constant rate 𝜃̇ 0 = 12 rad/s, determine for any given value of u (a) the radial and transverse components of the resultant force F exerted on pin B, (b) the forces P and Q exerted on pin B by rod OC and the wall of slot DE, respectively. Problem 12.80 Communication satellites are placed in a geosynchronous orbit, i.e., in a circular orbit such that they complete one full revolution about the earth in one sidereal day (23.934 h), and thus appear stationary with respect to the ground. Determine (a) the altitude of these satellites above the surface of the earth, (b) the velocity with which they describe their orbit. Give the answers in SI units. Problem 13.1 A 1300-kg small hybrid car is traveling at 108 km/h. Determine (a) the kinetic energy of the vehicle, (b) the speed required for a 9000-kg truck to have the same kinetic energy as the car. Problem 13.4 A 4-kg stone is dropped from a height h and strikes the ground with a velocity of 25 m/s. (a) Find the kinetic energy of the stone as it strikes the ground and the height h from which it was dropped. (b) Solve part a, assuming that the same stone is dropped on the moon. (Acceleration of gravity on the moon 5 1.62 m/s2.) Problem 13.9 A package is projected 10 m up a 15° incline so that it just reaches the top of the incline with zero velocity. Knowing that the coefficient of kinetic friction between the package and the incline is 0.12, determine (a) the initial velocity of the package at A, (b) the velocity of the package as it returns to its original position. Problem 13.10 A package is projected up a 15° incline at A with an initial velocity of 8 m/s. Knowing that the coefficient of kinetic friction between the package and the incline is 0.12, determine (a) the maximum distance d that the package will move up the incline, (b) the velocity of the package as it returns to its original position. 13.62 A 3-kg collar can slide without friction on a vertical rod and is resting in equilibrium on a spring. It is pushed down, compressing the spring 150 mm, and released. Knowing that the spring constant is k 5 2.6 kN/m, determine (a) the maximum height h reached by the collar above its equilibrium position, (b) the maximum speed of the collar. Problem 13.85 While describing a circular orbit 300 km above the earth a space vehicle launches a 3600-kg communications satellite. Determine (a) the additional energy required to place the satellite in a geosynchronous orbit at an altitude of 35 770 km above the surface of the earth, (b) the energy required to place the satellite in the same orbit by launching it from the surface of the earth, excluding the energy needed to overcome air resistance. (A geosynchronous orbit is a circular orbit in which the satellite appears stationary with respect to the ground.) Problem 13.119 A 1200-kg automobile is moving at a speed of 90 km/h when the brakes are fully applied, causing all four wheels to skid. Determine the time required to stop the automobile (a) on dry pavement (μk = 0.75), (b) on an icy road (μk = 0.10). Problem 13.166 Two identical hockey pucks are moving on a hockey rink at the same speed of 3 m/s and in parallel and opposite directions when they strike each other as shown. Assuming a coefficient of restitution e 5 1, determine the magnitude and direction of the velocity of each puck after impact. Problem 14.1 An airline employee tosses two suitcases, of mass 15 kg and 20 kg, respectively, onto a 25-kg baggage carrier in rapid succession. Knowing that the carrier is initially at rest and that the employee imparts a 3-m/s horizontal velocity to the 15-kg suitcase and a 2-m/s horizontal velocity to the 20-kg suitcase, determine the final velocity of the baggage carrier if the first suitcase tossed onto the carrier is (a) the 15-kg suitcase, (b) the 20-kg suitcase. Problem 14.9 A system consists of three particles A, B, and C. We know that mA = 3 kg, mB = 4 kg, and mC = 5 kg and that the velocities of the particles expressed in m/s are, respectively, vA = - 4i + 4j + 6k, vB = - 6i + 8j + 4k, and vC = 2i - 6j - 4k. Determine (a) the position vector r of the mass center G of the system, (b) the linear momentum mv of the system, (c) the angular momentum HG of the system about G. Problem 14.38 In a game of pool, ball A is moving with the velocity v0 = v0i when it strikes balls B and C, which are at rest side by side. Assuming frictionless surfaces and perfectly elastic impact (i.e., conservation of energy), determine the final velocity of each ball, assuming that the path of A is (a) perfectly centered and that A strikes B and C simultaneously. Problem 15.18 The circular plate shown is initially at rest. Knowing that r = 200 mm and that the plate has a constant angular acceleration of 0.3 rad/s2, determine the magnitude of the total acceleration of point B when (a) t = 0, (b) t = 2 s, (c) t = 4 s. Problem 15.31 A pulley and two loads are connected by inextensible cords as shown. The pulley starts from rest at t = 0 and is accelerated at the uniform rate of 2.4 rad/s2 clockwise. At t = 4 s, determine the velocity and position (a) of load A, (b) of load B. Problem 15.40 Small wheels have been attached to the ends of rod AB and roll freely along the surfaces shown. Knowing that wheel A moves to the left with a constant velocity of 1.5 m/s, determine (a) the angular velocity of the rod, (b) the velocity of end B of the rod. Problem 15.58 In the engine system shown in Figure, l = 160 mm and b = 60 mm. Knowing that crank AB rotates with a constant angular velocity of 1000 rpm clockwise, determine the velocity of the piston F and the angular velocity of the connecting rod when θ = 60°. Problem 15.65 In the position shown on Figure below, bar AB has an angular velocity of 4 rad/s clockwise. Determine the angular velocity of bars BD and DE. 15.84 Rod ABD is guided by wheels at A and B that roll in horizontal and vertical tracks. Knowing that at the instant β = 60° and the velocity of wheel B is 4 m/s downward, determine (a) the angular velocity of the rod, (b) the velocity of point D. Problem 15.89 Rod AB can slide freely along the floor and the inclined plane. Knowing that θ = 20°, β = 50°, l = 0.6 m, and vA = 3 m/s, determine (a) the angular velocity of the rod, (b) the velocity of end B. Problem 15.125 Knowing that crank AB rotates about point A with a constant angular velocity of 900 rpm clockwise, determine the acceleration of the piston P when θ = 60°. Problem 15.152 Two rotating rods (left) are connected by slider block P. The velocity v0 of the slider block relative to the rod is constant and is directed outwards. For the given data, determine the angular velocity of each rod in the position shown below. Given data b = 300 mm, v0 = 480 mm/s. Problem 16.27 The 180-mm-radius disk is at rest when it is placed in contact with a belt moving at a constant speed. Neglecting the weight of the link AB and knowing that the coefficient of kinetic friction between the disk and the belt is 0.40, determine the angular acceleration of the disk while slipping occurs. Problem 16.85 A uniform rod of length L and mass m is supported as shown below. If the cable attached at end B suddenly breaks, determine (a) the acceleration of end B, (b) the reaction at the pin support. Problem 16.124 The 4-kg uniform rod ABD is attached to the crank BC and is fitted with a small wheel that can roll without friction along a vertical slot. Knowing that at the instant shown crank BC rotates with an angular velocity of 6 rad/s clockwise and an angular acceleration of 15 rad/s2 counterclockwise, determine the reaction at A. Problem 17.2 The rotor of an electric motor has an angular velocity of 3600 rpm when the load and power are cut off. The 50-kg rotor, which has a centroidal radius of gyration of 180 mm, then coasts to rest. Knowing that the kinetic friction of the rotor produces a couple of magnitude 3.5 Nm, determine the number of revolutions that the rotor executes before coming to rest. Problem 17.5 The flywheel of a punching machine has a mass of 300 kg and a radius of gyration of 600 mm. Each punching operation requires 2500 J of work. (a) Knowing that the speed of the flywheel is 300 rpm just before a punching, determine the speed immediately after the punching. (b) If a constant 25-Nm couple is applied to the shaft of the flywheel, determine the number of revolutions executed before the speed is again 300 rpm. Problem 17.18 A slender rod of length l and weight W is pivoted at one end as shown. It is released from rest in a horizontal position and swings freely. (a) Determine the angular velocity of the rod as it passes through a vertical position and determine the corresponding reaction at the pivot. (b) Solve part a for W = 1.8 lb and l = 3 ft. Problem 17.60 The 350-kg flywheel of a small hoisting engine has a radius of gyration of 600 mm. If the power is cut off when the angular velocity of the flywheel is 100 rpm clockwise, determine the time required for the system to come to rest.