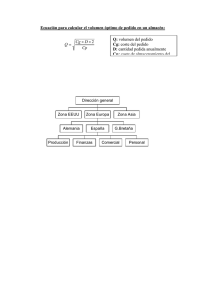
Problema 1. El supermercado local compra lechuga todos los días para asegurar la frescura del producto. Cada mañana, cualquier lechuga que haya quedado del día anterior se vende a un distribuidor que la revende a los granjeros para que alimenten a sus animales. Esta semana, el supermercado puede comprar lechuga a fresca a 4 dólares la caja, la lechuga se vende en 10 dólares la caja y el distribuidor que vende la lechuga remanente está dispuesto a pagar 1,50 dólares por caja. La experiencia establece que la demanda promedio de lechuga para mañana es de 250 cajas con una desviación estándar de 34 cajas. ¿Cuántas cajas de lechuga debe comprar el supermercado mañana? SOLUCIÓN A: Datos iniciales: Demanda promedio (đ) = 250 cajas por día. Tiempo de entrega en Días (L) = 7 días = 1 semana Desviación estándar (σL) = 34 cajas. Costo de compra = $ 4 caja. Costo de venta= $ 10 caja Costo remanente= $ 1,50 caja. Costo Compra=4 Precio Venta=$10 Precio Reventa=$1,5 D=200 cajas σ=34 cajas P≤ cu = Co+cu P= 10-4 =0.70 (4-1.5)+6 Z=0.54 Pedido=250-(0.54*34)=231.6 D=125 σ=15 Cu=125 250+125 Co=250 Z = 0.44 Pedido = 25-(0.44*15) =18.4 asientos P≤ 125 = 0.33 3- rays satellite emporiumquiere determinar el mejor tamaño de pedido para su antena que mas se vende. Ray estimo que la demanda anual para este modelo será de 1000 ud su costo por manejar una unidad es de 100 dólares al año y estima que cada pedido cueste 25 dólares. Utilizando el modelo EOQ ¿Cuánta unidades debe pedir ray cada vez? D= 1000 ud H= 100 us S= 25 us 4) 5 )Charli’es Pizza pide el pepperoni,las aceitunas, las anchoas y el queso mozzarella directamente a Italia. Un distribuidor estadounidense llega cada 4 semanas a levantar el pedido. Como los pedidos se envian desde Italia, tardan tres semanas en llegar. Charli’es Pizza utiliza un promedio de 150 libras de pepperoni a la semana con una σ=30 libras. Charli’es se enorgullece de ofrecer solo ingredientes de la mejor calidad y un alto nivel de servicio, de modo que quiere asegurar una probabilidad de 98% de que no quedarse sin pepperoni. Suponga que el representante de ventas acaba de llegar y que hay 500 libras de pepperoni en el congelador. ¿Cuantas libras de pepperoni debe pedir? T=4semanas ; L=3semanas ; dem.prom=150 ; σ=30 ; z=98% = 2.05 ; I=500 q= d.prom (T+L) + z σ(T+L) – I σ(T+L)= √ (4 +3)( 30 ) 2 = 79.37 q=150(7) + 2.05 (79.37) – 500 = 712,70 libras 6) Dada la información siguiente, formule un sistema de manejo de inventario la demanda, del producto abarca 50 semanas del año. Costo de la pieza 10$ Costo del pedido 250.00$ Costo de mantenimiento anual 33% del costo de la pieza Demanda promedio 515por semana Demanda anual 25750 Desviación estándar de la demanda semanal 25 por semana Tiempo de entrega 1 semana Probabilidad del servicio 95% a) Cantidad del pedido y el punto de reorden. Qopt= Datos : 2 DS /¿ H √¿ S= 250.00 H=3.3 D=25750Ā √ 2∗25750∗250.00 / 3.3 Qopt= = 1975.22 UNIDADES D Q 25750 1975.22 ∗3.3 S + H = 0*25750+ *250+ 2 Q 2 1975.22 CT= CD+ =6518.21$ R= đ L + ZσL D= 515 L= 1 Z= 1.6 σL= 25 R: 515*1+1.6*25 R: 555unid b) Determine los costos de mantenimiento y pedido anuales. Costo por pedir: D 25750 ∗S = ∗250.00 Qopt 1975.22 Costo por pedir= 3259.13 Costo mantenimiento: c) CT= 0*25750+ Q ∗H 2 = 1975.22 ∗3.3 = 3259.11 2 25750 2000 ∗200 ∗3.3 + =5875$ 2000 2 8)JILLS JOB SHOP compra dos piezas(tegdiws y widgets) para utilizarlas en su sistema de producción a dos proveedores diferentes. Las piezas se necesitan durante todo el año de 52 semanas. Los tegdiws se usan a un ritmo relativamente constante y se piden siempre que la calidad restante baja al nivel de volver a pedir.los widgets se piden a un proveedor que llega cada tres semanas. Los datos de ambos productos son los siguientes: ARTICULO TEGDIW WIDGET Demanda anual 10.000 5.000 Costo mantenimiento 20% 20% Costo de preparación o pedido $150,00 $25,00 Tiempo de entrega 4 semanas Una semana Inventarios de seguridad 55 unidades 5 unidades costo de pieza $10,00 $2,00 a) ¿Cual es el sistema de control de inventario para los tegdiws? Es decir, que cantidad se debe volver a pedir y en que punto? b) ¿Cual es el sistema de control de inventario para los widgets? c) D= $10.000 d) D= $10.000 H= 0.2X10 S= $150 Reemplazando; Q= 1224,74 aproximadamente 1225 unidades R= dL+ zoL d= 10.000/52 unidades/semanas L= 4 semanas oL= 55 unidades R=(10.000/52)(4)+(55) R= 824,23 Aproximadamente 824 unidades b) q= d(T+L)+zoT+L-I oT+L= oT+L = 10 d= 5.000/52 unidades/semanas L=1 semana T=3 semanas I= 5 unidades Reemplazando: q= 389,61 Aproximadamente 390-existencias en inventario EJERCICIO Nº 9 a. D=1000 unds Qopt= √ 2 DS H costo pedido= 10 u.s Qopt= √ costo mantener inventario= 2 u.s 2 (1000 ) (10 ) = 100 2 b. descuento de 100 dólares por si se piden ≥ 500 CT = D.C + D Q CT = 1.000(0) + S+ Q 2 H 1.000 100 (10)+ 1.000 500 (-90)+ 100 2 (2) CT = $ 200 CT = 1.000(0) + 500 2 (2) CT = $320 Se debe pedir de 100 unidades (pedido) EJERCICIO NÚMERO 10 Demanda anual: 15600 und Demanda semanal: 300 und Desviación estándar: 90 und Costo de la orden: $31.20 Tiempo de entrega: 4 semanas Costo de mantener inventario: $0.10 und anual Probabilidad de servicio: 98% R=dL+ zσl X1 X X2 0.97982 0.98000 0.998214 Z1 Z Z2 2.05 Z= 2.10 (2.10 – 2.05) x (0.9800 – 0.97982) +2.05 (0.98214 – 0.97982) Z = 2.053 σL = √ 902 + 902 + 902 + 902 σL = 180 R = (300)*(4) + (2.053*180) R= 1569.54 SS= Z σL (369.54-150) = z*180 Z= 1.21 11) La demanda diaria de un producto es de 100 unidades, con una desviación estándar de 25 unidades. El periodo de revisión es de 10 días y el tiempo de entrega es de 6 días. En el momento de la revisión hay 50 unidades en existencia. Si se desea una probabilidad de servicio de 98% ¿Cuantas unidades se deben pedir? Datos Demanda 100 unidades Desv. Estándar 25 unidades Periodo de revisión 10 días Tiempo de entrega 6 días Unid. En existencia 50 unidades Probabilidad 98% δ т + ʟ= ((10 + 6)(25)2)1/2 δ т + ʟ= 100 z= 2,05 q= ₫ (т + ʟ ) + z δ т + ʟ - I q= 100(10 + 6) + 2,05 (100)- 50 q= 1755 unidades 12)El elemento X es una pieza estándar almacenado en el inventario de componentes de una compañía. Cada año, la empresa, en forma aleatoria, utiliza alrededor de 2.000 unidades de la pieza, que cuestan 25 dólares cada una. Los costos de almacenamiento, que incluyen seguro y costo de capital, son de 5 dólares por unidad de inventario promedio. Cada que se hace un pedido de mas elemento X, el costo es de 10 dólares. a) Siempre que se pida el elemento X, ¿cual debe ser el tamaño del pedido? b) ¿Cual es el costo anual por pedir el elemento X? c) ¿Cual es el costo anual por almacenar el elemento X? a) D= 2.000 S= $10 H= 5 Reemplazando Q=89,44 Aproximadamente 89 unidades. b) Costo total de pedido anual= (D/Q)S CTPA= (2.000/89)10 CTPA= 224,71 dólares. c) Costo total de almacenamiento anual= (Q/2)H CTAA= (89/2)5 CTAA= 222,5 dolares. D= 13000 unidades d= 250 unidades σ= 40 S= 100 L= 4 3 Qopt= (¿¿ 13000∗100 )/ 0.65 √¿ §=Z σL σL= √ (4*(40)^2) =80 §=2.33*80= 186.4 H= 0.65 186.4-100=Z*80 P= 98% Z=86.4 =1.08 Z= 2.33 80 =2000 15)En el pasado, Taylor industries utilizaba un sistema de inventario fijo que comprendía contar todas las piezas del inventario cada mes. Sin embargo, los costos de mano de obra en aumento obligan a Taylor industries a estudiar formas alternativas de reducir la cantidad de mano de obra que participa en los almacenes, pero sin aumentar otros costos, como los de almacenamiento. Esta es una muestra aleatoria de 20 piezas de Taylor. Numero de pieza Uso anual ($) Numero Uso anual ($) de pieza 1 1.500 11 13.000 2 12.000 12 600 3 2.200 13 42.000 4 50.000 14 9.900 5 9.600 15 1.200 6 750 16 10.200 7 2.000 17 4.000 8 11.000 18 61.000 9 800 19 3.500 10 15.000 20 2.900 TOTAL DE USO ANUAL: $253.150 a) ¿Qué le recomendaría a Taylor para reducir su costo de mano de obra? (ilustre su respuesta usando un plan ABC) b) La pieza 15 es crucial para las operaciones continuas.¿ Como recomendaría clasificarlo? A) Numero de pieza Uso anual Porcentaje ($) valor total(%) Numero de pieza Uso anual ($) 18 61.000 24,1 17 4.000 4 50.000 19,75 19 3.500 13 42.000 16,59 20 2.900 10 15.000 5,93 3 2.200 11 13.000 5,14 7 2.000 2 12.000 4,74 1 1.500 8 11.000 4,35 15 1.200 16 10.200 4,03 9 800 14 9.900 3,91 6 750 5 9.600 3,79 12 600 Clasificación Numero de pieza Uso anual en dólares($) Po A 18,4,13 153.000 60 B 10,11,2,8,16,14,5 80.700 31 C 17,19,20,3,7,1,15,9,6,12 19.450 7,6 b) A la pieza 15 se recomienda que se clasifique como A, debido a que es de suma importancia. D= 5000 Costo compra= 3 S= 10 H= 0.6 L= 3 d= 100 σ= 30 P= 95% Z= 1.64 a. Qopt = √ ((2*5000*10)/0.6) = 408,24 b. σL= √ (3*(30)^2)= 51.96 R= 100*3+1.64*51.96= 385.21 Ejercicio 17 Datos Relevantes: - Probabilidad de servicios 98%. Demanda 2400 unidades por año. Costo de pedido 5 dólares. Costo de mantenimiento 4 dólares anuales por unidad. Desviación estándar 4 unidades al día. Tiempo de entrega 7 días. 365 días al año. Q opt = √ 2 DS H Q opt = √ 2( 2400 )( 5) =77.45 unidades 4 q=dL+ Z σ L d= 2400 =6.57 365 σ L =√ 4 + 4 + 4 +4 +4 + 4 + 4 2 2 2 q=( 6.57 ) (7 ) + ( 2.05) ( 10.58 )=67.67 unidades 18) 2 2 2 2 = 10.58 z= 2.05 19) University Drug Pharmaceuticals pide sus antibióticos cada 2 semanas (14 días) cuando pasa un vendedor de una de las compañías farmacéuticas. La tetraciclina es uno de los antibióticos mas importantes, con una demanda promedio diaria de 2000 capsulas. La desviación estándar de la demanda diaria se deriva del análisis de las recetas de los últimos 3 meses y es de 800 capsulas. El pedido tarda 5 días en llegar. University quiere cubrir un 99% de las recetas. El vendedor acaba de llegar y en la actualidad hay 25000 capsulas en existencia. ¿Cuantas capsulas hay que pedir? T= 14 Dem.prom=2000 σ=800 L=5 z=99% = 2.34 σ(T+L)= √ (5+14)(80 0)2 = 3487.11 q= 2000 (19) + 2.34 (3487.11) – 25000 = 21159,83 capsulas 20. sally’s silk produce playeras que se venden sobre todo en eventos especiales. Sally trata de decidir cuantas debe producir para el próximo evento durante el evento mismo, que dura un dia. Sally puede vender las playeras en 20 dolares cada una. Sin embargo al terminar el evento, cualquier playera que no se haya vendido se venderá en cuatro dólares la pieza. A Sally le cuesta 8 dolares hacer una playera de estas. Utilizando el estimado Sally en cuanto a la demanda, ¿Cuántas debe producir para el próximo evento? Demanda Probabilidad 300 0.05 400 0.10 500 0.40 600 0.30 700 0.10 800 0.05 20-8=12 8-4=4 p= cu cu + co p= 12 =0.75 4 +12 Ejercicio 22 - Demanda 3500 mofles. Costo por pedido 50 dólares. Costo de mantenimiento 7.5 dólares. Desviación estándar 6 unidades al día. Tiempo de entrega 2 días. 300 días al año. Q opt = √ 2 DS H Q opt = √ 2( 3500 ) (50) =216.02 unidades 7.5 q=dL+Z σ L d= 3500 =11.66 300 σ L =√ 6 2+ 62 = 8.48 z= 1.28 q=( 11.66 )( 2) +( 1.28 ) (8.48 )=34.17 unidades 23)) NUMER O PIEZA USO ANUAL EN DOLARE S A 7000 K 80000 B 1000 L 400 C 14000 M 1100 D 2000 N 30000 E 24000 O 1900 F 68000 P 800 G 17000 Q 90000 H 900 R 12000 I 1700 S 3000 J 2300 T 32000 A) PUEDE SUGERIR UN SISTEMA PARA DISTRIBUIR EL TIEMPO DE CONTROL. RTA. BASÁNDONOS EN EL USO ANUAL EN DÓLARES, SE SUGIERE QUE EL VALOR DE CONTROL DE INVENTARIO REGULAR SE EXPRESE DE FORMA DECRECIENTE SEGÚN EL TIEMPO QUE TARDA B) ESPECIFIQUE DONDE SE UBICARA CADA PIEZA DE LA LISTA RTA.SEGUN EL TIEMPO QUE DEMORA EN EL TIEMPO DE INVENTARIO 24. después de la graduación usted decide hacerse socio de una tienda de artículos para oficina q existe desde hace varios años. Caminando por la tienda y los almacenes, encuentra una diferencia importante en los niveles de servicios. Algunos espacios depósitos de artículos están totalmente vacios; otros tienen existencias cubiertas de polvo y es obvio que han estado ahí desde hace mucho tiempo. Usted decide hacerse cargo del proyecto de establecer niveles de inventario consistentes para cubrir la demanda de los clientes. la mayor parte de las piezas se compran a unos distribuidores que llaman a la tienda una vez cada semanas. Como primer artículo para estudiar, elige el papel de impresión para comparadora. Examina los requisitos de ventas y las órdenes de compra y se da cuenta de que la demanda durante los últimos 12 meses fue de 5000 cajas . Utilizando una calculadora realice un muestreo de las demandas de algunos días. Estime que la desviación estándar de la demanda diaria es de 10 cajas asi mismo. Investigué esta cifra Costo por caja de papel 11 dólares Probabilidad de servicios deseado 98% La tienda está abierta todos los días El tiempo e entrega después de esta visita es de tres días Empleando este procedimiento Cuantas cajas de papel pediría si es, el día en que llama el vendedor hay cajas disponibles? đ= 5000 =13.69 365 L= 2 σ= 10 T= 14 días Inventario: 60 unidades q=đ ( T + L )+ Z ( σt + L) −I q=( 13.69 ) (17 ) +( 2.05 ) (41.23 ) −60 q=257.25 σt+l=√ ( T +L ) (σ ) 2 σt+l=√ ( 14 + 3 ) ( 10) 2 σt+l=41.23 25. una distribuidora de aparatos electrodomésticos grandes necesita determinar las cantidades de los pedidos y los puntos de reorden para los distintos productos que maneja. Lo datos siguientes se refieren a un refrigerador especifico en su línea de producto. Costo de hacer un producto: 100. Dólares Costo por tener inventario: 20% del costo del producto al año. Costo del refrigerador: 500 dólares cd Demanda anual: 500 refrigeradores Desviación estándar durante el tiempo de entrega: 10 refrigeradores Tiempo de entrega: 7 días Considere una demanda diaria uniforme y un año de 365 días. A) cuál es la cantidad económica de pedidos? √ Q= 2(500)( 100) 100 Q=31.622 B) si el distribuidor quiere una probabilidad de servicio de 97%, que punto de reorden, r, se debe usar? R=đL+ Z σl R= ( 1.36 )( 7 )+ ( 1.88 )( 26.46 ) R=59.2648 σl=√ (7 ) (10 ) 2 σl=26.45 26- como el nuevo jefe de la sección automotriz de Nichols Deparmet Store, tiene la responsabilidad de volver a partir las cantidades de distintos artículos que se han establecido en forma correcta. Usted decide probar una pieza y elige las llantas Michelin, xw tamaño 185 x 14 BSW. Se ha utilizado un sistema de inventarios perpetuo, de modo que lo analiza, al que otros registros, y obtiene la siguiente información: Cu = 35 dólares/unidad H = 20% del costo de las llantas al año S = dólares/pedido D = 1000 por año Desviación = 3 llantas L = 4 días Como los clientes casi nunca esperan que lleguen las llantas, si no que acuden a otra tienda, decide una probabilidad del servicio de 98% suponga que la demanda ocurre 365 días al año. a- Determinar la cantidad que hay que pedir b- Determinar el punto de reorden a- b- = = 6 ud R= (2.73) (4) + (2.05) (6) = 23.22 ud 27. U A hamburgués Hamlet (U A H H ) Hace un pedido diario de las piezas que utiliza en mayor volumen (panes de hamburguesa, carne, leche, etc.), UAHH cuenta su inventario disponible una vez al día y hace su pedido por teléfono, mismo que llega alas 24 horas. Determine el numero de hamburguesas que UAHH debe pedir para las condiciones siguientes: Demanda promedio diaria 600 Desviación estándar de la demanda 100 Probabilidad de servicio deseada Inventario de hamburguesas 99% 800 2(10000) = 141,42 QT+L= 2(10000) = 141,42 q= d(T+L) + Z Q (T+L)-I = q= (600) (2) + (2,37) (141,42)-(800) = 729 q= 729. 29) DAT, inc, produce cintas de audio digitales para utilizarlas en la división de audio para el consumidor. DAT no tiene el personal suficiente en su sección de suministro de inventario para controlar cada una de la piezas en existencia de modo que le pidió que determinara una clasificación ABC. Esta es una muestra de los registros del inventario. Desarrolle una clasificación ABC para estas 10 piezas PIEZA 1 2 3 4 5 6 7 8 9 10 PIEZA 5 7 3 8 DEMANDA MENSUAL PROMEDIO 700 200 2000 1100 4000 100 3000 2500 500 1000 DEMANDA MENSUAL PROMEDIO 4000 3000 2000 2500 PRECIO UNITARIO 6.00 4.00 12.00 20.00 21.00 10.00 2.00 1.00 10.00 2.00 PRECIO UNITARIO PORCENTAJE 21.00 2.00 12.00 1.00 23.86 2.27 13.63 1.13 1100 1000 700 500 200 100 4 10 1 9 2 6 20.00 2.00 6.00 10.00 4.00 10.00 88.00 22.72 2.27 5.28 11.36 4.54 11.36 100% PIEZA 5 4 3 6 9 1 2 7 10 8 PRECIO UNITARIO 21.00 20.00 12.00 10.00 10.00 6.00 4.00 2.00 2.00 1.00 PORCENTAJE 23.86 22.72 13.63 11.36 11.36 5.28 4.54 2.27 2.27 1.3 PIEZA DEMANDA PROMEDIO POR COSTO UNITARIO 84000 6000 24000 2500 22000 2000 4200 5000 800 1000 PORCENTAJE 5 3 4 7 9 1 8 10 6 2 A = 55.44% pieza 5 55.44 15.84 14.52 8.96 3.30 2.77 1.65 1.32 0.66 0.52 B = 14.84% + 14.52% = 30.36% pieza 3, pieza 4 C = 14.18% pieza 7, 9, 1, 8, 10, 6, 2 30 )Una estacion de servicio local esta abierta 7 dias a la semana, 365 dias al año. Las ventas promedio de aceite Premium 10W40 son de 20 latas al dia. Los costos de mantenimiento del inventario son de 0.50 dolares por lata al año. Los costos de pedido son 10 dolares cada uno. El tiempo de entrega es de 2 semanas. Con base en estos datos, seleccione el modelo de inventario apropiado y calcule la cantidad economica de pedido y el punto de reorden. Dem.prom= 20 por dia ; H=0.50 anual; S=10 dolares; L=2 semanas Qop= √ 2∗ (20∗365 )∗10 0.50 = 540.37 unid. R=dem.prom * L R= 20(14)= 280 unid. Al jefe le preocupa este modelo porque la demanda si varia. La desviacion estandar de la demanda determinada a partir de una muestra es de 6.15 latas por dia. El gerente quiere una probabilidad de servicio de 99.5%. R=dem.prom * L + z σ L σ= √ 14 (6.15 )2 = 23.01 R=20 (14) + 2.57 (23.01) = 339.13 unid. 31) 32. D= 10000 H= 14% valor del producto = 3.36 C= $24 S= $150 Qopt =√ Qopt =√ Qopt= 945 unidades CT = D.C + S + H CT = 10.000(24) + (150)+ (3.36) CT = $ 24374,90 32. Un detallista en línea watchesforless.com vende un estilo popular de reloj con cronometro deportivo. La demanda de este reloj en particular es de 10000 por año. El costo de mantener la unidad en el inventario durante un año es de 14% de su valor. Cada reloj cuesta 24 dólares. El costo de hacer un pedido con el proveedor es de 150 dólares. ¿Cuál es el costo anual total si watchesforless.com utiliza la de pedido de EOQ optima? D= 10000 unds/año c. pedido=150 dólares c. unidad=24 dólares c. mantener=24*0.14=3,36 Q.optimo= Q.optimo= Q.optimo=944,91 TC=D*C+((D/Q)*S)+((Q/2)*H) D*C=10000*24=240000 ((D/Q)*S)=(10000/944,91)*150 ((D/Q)*S)=1587,45 ((Q/2)*H)=(944,91/2)*3,36 ((Q/2)*H)=1587,44 TC=240000+1587,45+1587,44 TC=243174,89 dólares EJERCICIO 33: R = 2800 d = 500 Uds/ dia L = 5 días P = 94,3 % Z = 1,58 R = dL + ZσL 2800 = (500)(5) + 1,58σL 300 = 1,58σL σL= 189,87 Problema 34. Southern Hydraulic Supply lleva a cabo una revisión de sus políticas de inventario. Un producto típico es un pequeño accesorio hidráulico. En la actualidad, Southern pide 1000 accesorios a la vez. La demanda de los accesorios es de 52000 al año, el costo de pedido es de 50 dólares cada pedido y el costo de mantener un accesorio en el inventario durante un año es de 1,25 dólares. Cada unidad cuesta 8 dólares. a) ¿cuál es el costo total anual de la política de inventario actual de Southern? b) ¿Cuál es la cantidad optima a pedir? ¿cual es el costo total anual de la política optima? ¿cuánto puede ahorrar Southern al año cambiando a la política optima? c) Southern maneja 11000 piezas diferentes en su inventario. Como el accesorio hidráulico es “típico”, suponga que los ahorros también son típicos. ¿Cuánto puede ahorrar Southern al año cambiando todo su inventario a una política optima? SOLUCIÓN Datos iniciales Demanda (d) = 52000 accesorios- año Costo de Pedido (S)= $ 50 Costo de Inventario (H)= $ 1,25 año Costo por Unidad =$ 8 Paso 1, tomamos la formula de modelo Q. costo anual total de una Q pedido, un costo por unidad , el costo de preparación S y el costo de mantenimiento por unidad H. Q D S+ H 2 TC = DC + Q Paso 2, Calculamos el Qopt Qopt= Qopt= √ √ 2 DS H 2 ( 52000 )∗(50 ) 1 ,25 Qopt= 2039,6 unds Paso 3, reemplazamos en la formula del paso 1 TC = DC + TC = (52000)(8) + Q D S+ H Q 2 (52000 ) (2039,6 ) ( 1,25) ( 50) + 2 ( 2039,6 ) Respuestas a) el costo total anual de la política de inventario actual de Southern. $ 418.549,4. b) la cantidad optima a pedir es 2039,6 unds TC=