lalal
Anuncio
Árboles:
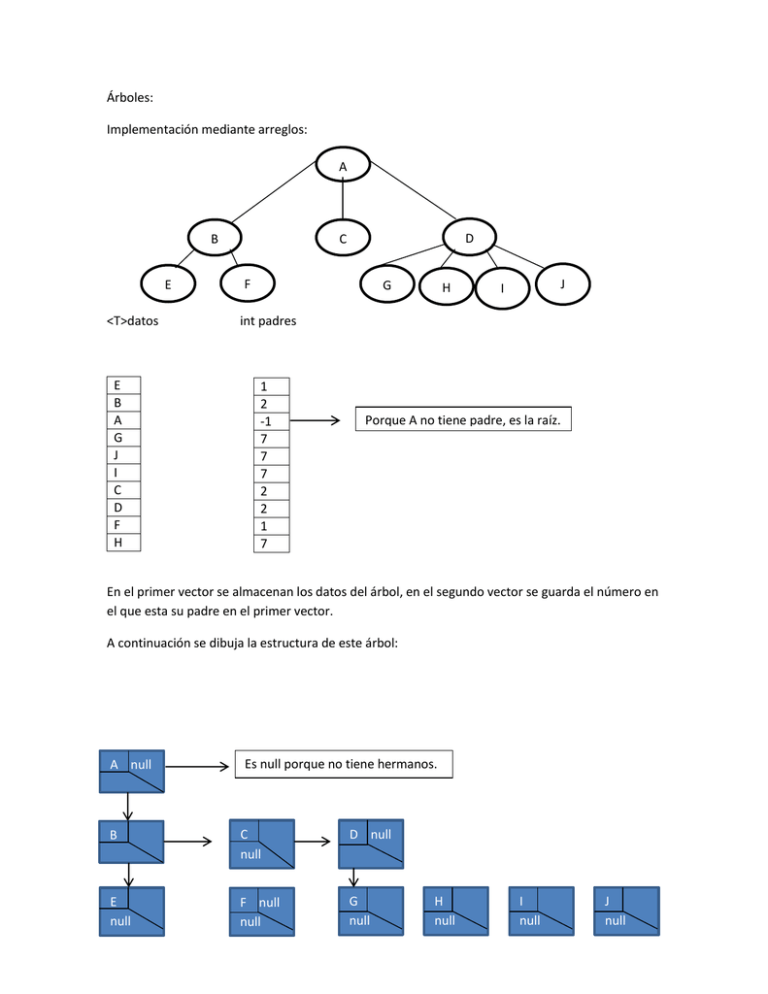
Implementación mediante arreglos:
A
B
E
<T>datos
E
B
A
G
J
I
C
D
F
H
D
C
F
G
H
J
I
int padres
1
2
-1
7
7
7
2
2
1
7
Porque A no tiene padre, es la raíz.
En el primer vector se almacenan los datos del árbol, en el segundo vector se guarda el número en
el que esta su padre en el primer vector.
A continuación se dibuja la estructura de este árbol:
A null
B
E
null
Es null porque no tiene hermanos.
C
null
null
F null
null
D null
G
null
H
null
I
null
J
null
Es null porque no tiene hijos.
Sub- clasificación de Árboles:
Árboles binarios:
Los árboles binarios son árboles en los cuales cada nodo puede tener un máximo de dos hijos.
Aplicaciones: Evaluación de expresiones aritméticas, búsqueda y ordenamiento, etc.
Terminología:
Incluye la terminología de los árboles generales, además de una clasificación qque indica su
inclinación.
Sub- árbol izquierdo.
Sub- árbol derecho.
D
A
No es un árbol binario
C
Siguiendo con la terminología de Árboles, se definen a continuación las características de los
árboles binarios:
-
Lleno: Todos los niveles del Árbol tienen el máximo de nodos. Son 2ℎ − 1 .
Degenerado: Todos los nodos (excepto las hojas) tienen un solo hijo.
Completo: Todos los nodos tienen el máximo de hijos posibles (dos), menos las hojas.
Balanceado: Para todos los nodos la diferencia entre la altura de su subárbol izquierdo y
la altura de su subárbol derecho es menor a 2.
Definamos las características de los siguientes 4 árboles binarios:
A
B
C
D
Árboles
Completo
Lleno
Degenerado
Balanceado
Implementación
A
X
X
B
X
X
X
C
D
X
X
X
X
Árbol binario:
A
C
B
D
E
F
Vectores
<T> datos
D
B
A
C
E
F
int izq
-1
0
1
4
1
-1
int der
-1
-1
3
5
-1
-1
Vemos en la implementación mediante vectores, en la cual se definen tres vectores: uno llamado
datos (datos de cada nodo), en la cual se guardan datos de tipo genérico; uno llamado izq, en el
cual se guarda la respectiva posición en el vector datos del hijo que está a su izquierda en el árbol
(para B es cero porque su hijo a la izquierda es D); otro llamado der, en el cual se almacenan las
posiciones en el vector datos de los hijos que están a la derecha en el árbol (para B es -1 porque
no tiene hijos a la derecha).
La estructura de un nodo de árbol binario tiene la siguiente estructura, en la cual se guarda un
dato, la dirección del hijo a la izquierda y la dirección del hijo a la derecha. En caso de no tener
hijos a la izquierda o a la derecha se indicará como “null” (vacío) con un “slash” (/).
Dato
Izq
der
Utilizando como ejemplo el árbol anterior, lo obtendríamos en esta estructura así:
A
B
D
C
E
F
El código en el cual se almacena la lógica para crear estos nodos es el siguiente, en dicha clase
aparecen los constructores, modificadores y analizadores necesarios.
Public class NodoArbolBin <T>{
Private T dato;
Private NodoArbolBin izq;
Private NodoArbolBin der;
Public NodoArbolBin(T dato){
This.dato=dato;
Izq=der=null;
}
Public void setIzq(NodoArbolBin izq){
This.izq=izq;
}
Public NodoArbolBin getIzq(){
Return izq;
}
Public void setDer(NodoArbolBin der){
This.der=der;
}
Public NodoArbolBin getDer(){
Return der;
}
}
Para dar un ejemplo de cómo funciona se crea un main, en el cual se creará el nodo con el dato A y
se le agregarán como hijos a la izquierda un nodo B, y a la derecha un nodo C.
Public class principal{
Public static void main (String[]arg){
NodoArbolBin raíz;
raiz=new NodoArbolBin(“A”);
raiz.setIzq(new NodoArbolBin(“B”));
raiz.setDer(new NodoArbolBin(“C”));
NodoArbolBin a=raíz.getIzq();
a.setIzq(new NodoArbolBin(“D”));
a=raíz.getDer();
a.setIzq(new NodoArbolBin(“E”));
a.setDer(new NodoArbolBin(“F”));
}
}
Recorridos:
Combinación de actividades para visitar todos los nodos y hacer las respectivas operaciones.
Actividades:
1. Visitar raíz (e imprimirla).
2. Recorrer subárbol izquierdo (recursiva).
3. Recorrer subárbol derecho (recursiva).
En las actividades recursivas, cada vez que se llegue ahí volverá a realizar la primera instrucción.
Combinaciones
Recorridos
1, 2, 3
Pre orden
2, 1, 3
In orden
2, 3, 1
Pos orden
Ahora, mostraremos como se muestran los datos de este árbol en las diferentes combinaciones:
A
C
B
D
E
F
Pre orden: raíz, izquierda, derecha: A, B, D, E, C, F
In orden: izquierda, raíz, derecha: D, B, E, A, F, C
Pos orden: izquierda, derecha, raíz: D, E, B, F, C, A



