SOLUCIONARIO SEMANA 3.
Ever Euceda Romero.
Ejercicio 1: En la siguiente figura se presentan la corriente y la tensión a través de
un elemento.
a) Trace la potencia suministrada al elemento en t > 0.
b) Halle la energía total absorbida por el elemento en el periodo 0 < t < 4 s.
Trazar potencia suministrada al elemento en t > 0.
Calculando.
𝑖 − 0 60 − 0 60
=
=
= 𝑖 = 30𝑚𝐴
𝑡−0
2−0
2
𝑹𝒆𝒔𝒑𝒖𝒆𝒔𝒕𝒂: 𝟑𝟎𝒕 𝒎𝑨 [𝟎 − 𝟐 𝑺]
𝑖 − 60
𝑡−2
0 − 60
60
=−
= −30
4−2
2
𝑖 − 60 = −30(𝑡 − 2)
𝑖 = −30(𝑡 − 2) + 60
Circuito Eléctrico – Sistemas Electromecánicos – Ingeniería Industrial
𝑖 = −30𝑡 + 60 + 60
𝑹𝒆𝒔𝒑𝒖𝒆𝒔𝒕𝒂: 𝒊 = −𝟑𝟎𝒕 + 𝟏𝟐𝟎 𝒎𝑨 [𝟐 − 𝟒 𝑺]
Encontrando la Potencia.
𝑃 = 𝑉𝑥𝐼
Entonces tenemos que la intensidad es:
𝑖(𝑡) = {
30𝑡 𝑚𝐴 [0 − 2𝑆]
20𝑡 + 120 𝑚𝐴 [2 − 4 𝑆]
Por otro lado, el voltaje según la gráfica.
𝑉(𝑡) = {
5𝑉 [0 − 2𝑆]
−5𝑉 [2 − 4 𝑆]
Aplicando la formula de potencia eléctrica para realizar el cálculo.
𝑃 = 𝑉𝑥𝐼
CALCULOS DE POTENCIA
𝒊(𝒕) = 𝟑𝟎𝒕 𝒎𝑨
[𝟎 − 𝟐𝑺], 𝑽(𝒕) = 𝟓𝑽
[𝟎 − 𝟐𝑺]
𝒊(𝒕) = 𝟐𝟎𝒕 + 𝟏𝟐𝟎 𝒎𝑨
[𝟐 − 𝟒 𝑺]𝒗(𝒕) = −𝟓𝑽 [𝟐 − 𝟒 𝑺]
𝑃 = 𝑉𝑥𝐼
𝑃 = 𝑉𝑥𝐼
𝑃 = (𝟓𝑽)(𝟑𝟎𝒕 𝒎𝑨)
𝑃 = (𝟓𝑽)(−𝟑𝟎𝒕 + 𝟏𝟐𝟎 𝒎𝑨)
𝑃 = 150𝑡 𝑚𝑊
𝑃 = 150𝑡 − 600 𝑚𝑊
Graficando los resultados.
Circuito Eléctrico – Sistemas Electromecánicos – Ingeniería Industrial
b) Halle la energía total absorbida por el elemento en el periodo 0 < t < 4 s.
𝑡
𝑤 = ∫ 𝑝𝑑𝑡
𝑡0
2
4
𝑤 = ∫ 150 𝑑𝑡 + ∫ 150𝑡 − 600 𝑑𝑡
0
𝑤 = 150
2
𝑡2 2
𝑡2 4
4
| + 150 | − 600𝑡 |
2 0
2 2
2
𝑤 = 75(4) + 75(16 − 4) − 600(4 − 2)
𝑤 = 300 + 1200 − 300 − 2400 + 1200
𝑹𝒆𝒔𝒑𝒖𝒆𝒔𝒕𝒂: 𝒘 = 𝟎 𝑱𝒐𝒖𝒍𝒆𝒔
Circuito Eléctrico – Sistemas Electromecánicos – Ingeniería Industrial
Ejercicio 2: En la siguiente figura se presenta un circuito con cinco elementos. Si p1
= -205 W, p2 = 60 W, p4 = 45 W, p5 = 30 W, calcule la potencia p3 recibida o
suministrada por el elemento 3.
Esquema de distribución de potencias.
Aplicando sumatoria de potencia para calcular la potencia del elemento 3.
∑𝑃 = 0
∑ 𝑃1 + 𝑃2 + 𝑃4 + 𝑃5 + 𝑃3 = 0
∑ −205𝑊 + 60𝑊 + 45𝑊 + 30𝑊 + 𝑃3 = 0
𝑃3 = 205𝑊 − 60𝑊 − 45𝑊 − 30𝑊
𝑃3 = 205𝑊 − 135𝑊
𝑹𝒆𝒔𝒑𝒖𝒆𝒔𝒕𝒂: 𝑷𝟑 = 𝟕𝟎𝑾
Circuito Eléctrico – Sistemas Electromecánicos – Ingeniería Industrial
Ejercicio 3: Halle la potencia absorbida por cada uno de los elementos en la
siguiente figura
Como se nos pide calcular la potencia absorbida por cada uno de los
elementos aplicamos la formula P=VxI de la Ley de Ohm.
CALCULANDO LAS INTENSIDADES CON 𝑷 = 𝑽𝒙𝑰
𝑃1
𝑷 = 𝟑𝟎𝑽(−𝟏𝟎𝑨) = −𝟑𝟎𝟎𝑾
𝑃2
𝑷 = 𝟔𝟎𝑽(𝟏𝟎𝑨) = 𝟔𝟎𝟎𝑾
𝑃3
𝑷 = 𝟐𝟎𝑽(𝟏𝟒𝑨) = 𝟐𝟖𝟎𝑾
𝑃4
𝑷 = 𝟖𝑽(−𝟒𝑨) = −𝟑𝟐𝑾
𝑃5
𝑷 = 𝟏𝟐𝑽(−𝟒𝑨) = −𝟒𝟖𝑾
Circuito Eléctrico – Sistemas Electromecánicos – Ingeniería Industrial
Ejercicio 4: Halle I y la potencia absorbida por cada uno de los elementos en la red
de la siguiente figura:
Paso 1: Calculando la Intensidad, como sabemos que nos dan la intensidad de las
dos mallas entonces las restamos
𝐼 = 𝐼1 − 𝐼2
𝐼 = 8𝐴 − 2𝐴 = 6𝐴
𝑹𝒆𝒔𝒑𝒖𝒆𝒔𝒕𝒂: 𝟔𝑨
Paso 2: Calcular la potencia absorbida por cada uno de los 4 elementos.
CALCULANDO LAS INTENSIDADES CON 𝑷 = 𝑽𝒙𝑰
𝐄𝐥𝐞𝐦𝐞𝐧𝐭𝐨 𝐝𝐞 𝟖𝐀 = 𝑷 = −𝟖𝑽(𝟗𝑨) = −𝟕𝟐𝑾
𝐄𝐥𝐞𝐦𝐞𝐧𝐭𝐨 𝐝𝐞 𝟗𝐕 = 𝑷 = 𝟗𝑽(𝟐𝑨) = 𝟏𝟖𝑾
𝐄𝐥𝐞𝐦𝐞𝐧𝐭𝐨 𝐝𝐞 𝟑𝐕 = 𝑷 = 𝟑𝑽(𝟔𝑨) = 𝟏𝟖𝑾
𝑬𝒍𝒆𝒎𝒆𝒏𝒕𝒐 𝒅𝒆 𝟔𝑽 = 𝑷 = 𝟔𝑽(𝟔𝑨) = 𝟑𝟔𝑾
Circuito Eléctrico – Sistemas Electromecánicos – Ingeniería Industrial
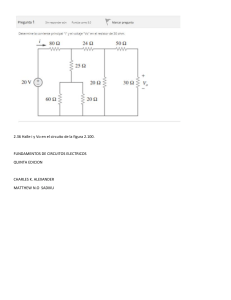
Ejercicio 5: Halle Vo y la potencia absorbida por cada elemento en el circuito en
la figura:
Paso 1: Calcular la potencia de los elementos que no tienen incógnitas.
CALCULANDO LAS INTENSIDADES CON 𝑷 = 𝑽𝒙𝑰
𝐄𝐥𝐞𝐦𝐞𝐧𝐭𝐨 𝐝𝐞 𝟑𝟎𝐕 = 𝑷 = 𝟑𝟎𝑽(−𝟔𝑨) = −𝟏𝟖𝟎𝑾
𝐄𝐥𝐞𝐦𝐞𝐧𝐭𝐨 𝐝𝐞 𝟏𝟐𝐕 = 𝑷 = 𝟏𝟐𝑽(𝟔𝑨) = 𝟕𝟐𝑾
𝑬𝒍𝒆𝒎𝒆𝒏𝒕𝒐 𝒅𝒆 𝟑𝑨 = 𝑷 = 𝑽𝟎 (𝟑𝑨) = 𝟑𝑽𝟎
𝐄𝐥𝐞𝐦𝐞𝐧𝐭𝐨 𝐝𝐞 𝟐𝟖𝐕 = 𝑷 = 𝟐𝟖𝑽(𝟐𝑨) = 𝟓𝟔𝑾
𝐄𝐥𝐞𝐦𝐞𝐧𝐭𝐨 𝐝𝐞 𝟐𝟖𝐕 = 𝑷 = 𝟐𝟖𝑽(𝟏𝑨) = 𝟐𝟖𝑾
𝑬𝒍𝒆𝒎𝒆𝒏𝒕𝒐 𝒅𝒆 𝟓𝑰𝟎 = 𝑷 = 𝟓𝑿𝟐𝑽(𝟑𝑨) = −𝟑𝟎𝑾
Paso 2: Aplicar sumatoria de potencia par calcular la potencia del punto V0
∑𝑃 = 0
∑ 𝑃1 + 𝑃2 + 𝑃4 + 𝑃5 + 𝑃6 + 𝟑𝑽𝟎 = 0
∑ −180𝑊 + 72𝑊 + +56 + 28𝑊 − 30𝑊 + 𝟑𝑽𝟎 = 0
𝟑𝑽𝟎 = 180𝑊 − 72𝑊 − 56𝑊 − 28𝑊 + 30𝑊
𝟑𝑽𝟎 = 180𝑊 − 126𝑊
𝑹𝒆𝒔𝒑𝒖𝒆𝒔𝒕𝒂: 𝟑𝑽𝟎 = 𝟓𝟒𝑾
Paso 3: Calcular la potencia del elemento faltante.
𝟑𝑽𝟎 = 𝟓𝟒𝑾
𝑹𝒆𝒔𝒑𝒖𝒆𝒔𝒕𝒂: 𝑷𝑽𝟎 =
𝟓𝟒𝑾
= 𝟏𝟖𝑽
𝟑𝑨
Circuito Eléctrico – Sistemas Electromecánicos – Ingeniería Industrial