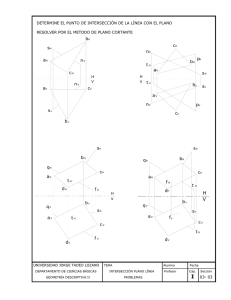
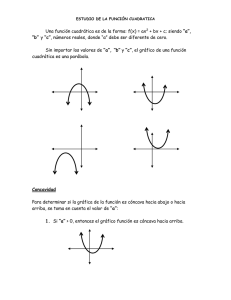
AMERICAN JUNIOR COLLEGE Guía Función Cuadrática MISTER: Jaime Sanhueza DATE: SUBJECT: Matemática 2 OA: Mostrar que comprenden la función cuadrática 𝑓(𝑥) = 𝑎𝑥 + 𝑏𝑥 + 𝑐 (𝑎 ≠ 0) STUDENT: Grade: INDICATOR I II L ML N L Calculan imágenes de valores de funciones cuadráticas. Determinan los elementos principales de la parábola (concavidad, vértice y puntos de intersección). Función Cuadrática: 𝒇(𝒙) = 𝒂𝒙𝟐 + 𝒃𝒙 + 𝒄 Concavidad: 𝒂 > 𝟎 Cóncava hacia arriba 𝒂 < 𝟎 Cóncava hacia abajo Vértice: 𝑽 (− 𝑽 (− 𝒃 𝒃 , 𝒇 (− )) 𝟐𝒂 𝟐𝒂 𝒃 𝒃𝟐 − 𝟒𝒂𝒄 ,−( )) 𝟐𝒂 𝟒𝒃 Punto(s) de intersección con el Eje X (si es Punto de intersección con el Eje Y (siempre que existen): existe intersección): 𝒙𝟏 = 𝒙𝟐 = −𝒃 + √𝒃𝟐 − 𝟒𝒂𝒄 𝟐𝒂 −𝒃 − √𝒃𝟐 − 𝟒𝒂𝒄 𝟐𝒂 𝑷𝟏 (𝒙𝟏 , 𝟎) ; 𝑷𝟐 (𝒙𝟐 , 𝟎) Si 𝒃𝟐 − 𝟒𝒂𝒄 < 𝟎, la parábola no tiene puntos de intersección con el Eje X. 𝑷𝟑 (𝟎, 𝒇(𝟎)) 𝑷𝟑 (𝟎, 𝒄) I. Calcula la imagen de los siguientes valores para cada una de las funciones cuadráticas correspondientes: a) 𝒇(𝒙) = 𝟑𝒙𝟐 + 𝟓𝒙 − 𝟐 𝑓(2) = 𝑓(−3) = 𝑓(0) = 1 𝑓( ) = 2 b) 𝒇(𝒙) = −𝟒𝒙𝟐 + 𝟔𝒙 𝑓(−5) = 𝑓(−3) = 2 𝑓( ) = 3 𝑓(10) = c) 𝒇(𝒙) = −𝟔𝒙𝟐 + 𝟖𝒙 + 𝟐 𝑓(3) = 𝑓(−7) = 𝑓(2) = 4 𝑓( ) = 3 II. En tu cuaderno, determina la concavidad, coordenadas del vértice e intersecciones con los ejes coordenados de las siguientes funciones cuadráticas: a) 𝑓(𝑥) = 2𝑥 2 − 8𝑥 + 6 b) 𝑓(𝑥) = −2𝑥 2 + 2𝑥 + 12 c) 𝑓(𝑥) = 𝑥 2 − 𝑥 − 20 d) 𝑓(𝑥) = 𝑥 2 + 4𝑥 − 3 e) 𝑓(𝑥) = 4𝑥 2 + 12𝑥 + 9 f) 𝑓(𝑥) = 𝑥 2 + 2𝑥 + 5 g) 𝑓(𝑥) = 𝑥 2 − 2𝑥 + 1 h) 𝑓(𝑥) = 2𝑥 2 − 6𝑥 i) 𝑓(𝑥) = 𝑥 2 + 𝑥 − 6